基于电流矢量角的IPMSM最大转矩电压比深度弱磁控制

肖焯夫，张代润

（四川大学电气工程学院，四川 成都 610065）

内置式永磁同步电机（interior permanent magnet synchronous motors，IPMSM）具有效率高、功率密度大、启动转矩大、弱磁能力强以及结构紧凑等优点[1-3]，被广泛应用于电动汽车、家电、伺服系统、航空航天、船舶等工业驱动系统中。当IPMSM的特征电流位于电流极限圆内时，考虑驱动系统受到的电流和电压限制，IPMSM在id-iq平面内的电流轨迹可分为3个部分[4]：最大转矩电流比（maximum torque per ampere，MTPA）轨迹OC段、普通弱磁区、最大转矩电压比（maximum torque per voltage，MTPV）轨迹EF段，如图1所示，普通弱磁区包括电流极限圆CE段、恒转矩曲线BD段、恒转矩曲线AE段等。控制IPMSM电流工作点运行在MTPV轨迹上，实现深度弱磁，可进一步扩大电机的调速范围以及高速带载能力，不需要额外增加直流母线电压和逆变器功率，节省成本。

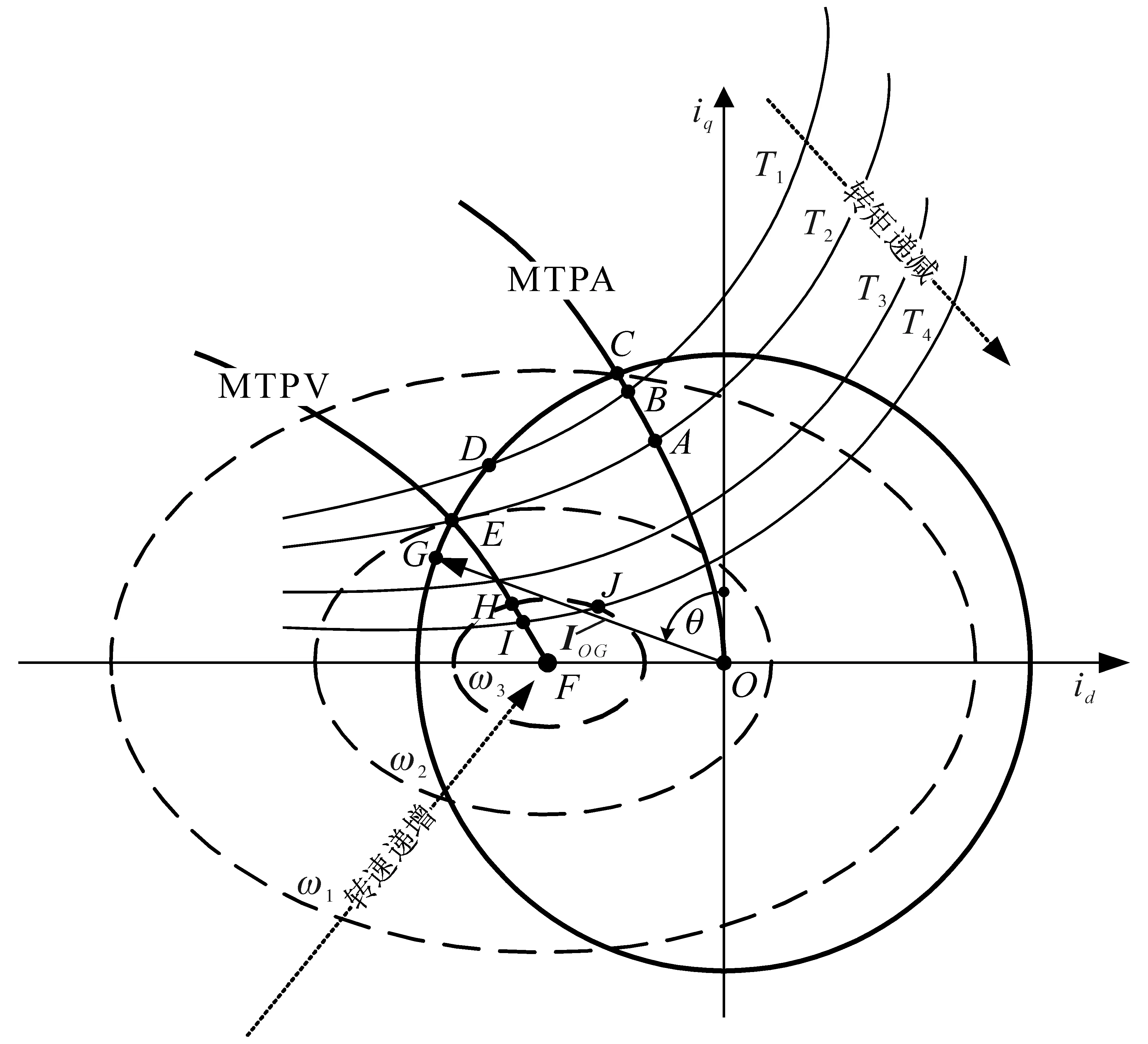
图1 IPMSM在id-iq平面中的电流轨迹Fig.1 The current trajectory of IPMSM in the id-iqplane

以往文献中，提出了许多弱磁算法及其改进算法来实现MTPV控制。直接磁链矢量控制法[5]通过控制磁链矢量幅值以及控制磁链矢量角为最大负载角来线性化MTPV轨迹，其中最大负载角需要通过多次空载测试才能得到最佳值。梯度下降法[6]通过恒转矩曲线方向与电压递减方向判断当前电流工作点位于普通弱磁区还是MTPV轨迹，根据所在的弱磁区域以及电压差计算直轴和交轴电流补偿量，实现MTPV控制，该算法计算很复杂。查表法[7-9]利用电机标定数据生成电流二维表，通过实时查表获取直轴电流和交轴电流设定值，实现MTPV控制，但电机标定工作量大，不同型号的电机需要单独标定。单电流调节器弱磁法[10-12]解决了传统双电流调节器的冲突问题，但是需要合适的开关规则才能实现MTPA轨迹与普通弱磁区的平滑切换。其中，文献[12]取电压矢量幅值恒为逆变器最大输出电压，通过控制电压矢量角为一固定值来线性化MTPV轨迹。PWM脉宽弱磁法[13]将PWM脉宽与PWM周期作差，经过PI控制器生成直轴电流偏移量实现普通弱磁，通过修改算法，利用实际转速计算MTPV轨迹上的直轴和交轴电流，以计算得到的电流值作为设定值来实现MTPV控制。在众多弱磁控制算法中，电压外环反馈法[14]受到了广泛关注与研究，通过电压外环反馈回路生成直轴电流偏移量实现普通弱磁。文献[15]在电压外环反馈法的基础上进行修改，提出了基于直轴电流差的MTPV控制算法，通过对直轴电流设置下限，得到限幅前后的直轴电流差，经过比例控制器生成交轴电流变化量，得到交轴电流设定值，代入MTPV轨迹方程计算得到直轴电流设定值，从而实现MTPV控制。

由图1可知，控制电机电流工作点沿着MT⁃PV轨迹运行，当电机转速为ω3以及负载转矩为T4时，电机电流工作点从MTPV轨迹H点沿着电压极限椭圆进入普通弱磁区并稳定运行在J点所需电流幅值小于稳定运行在MTPV轨迹上I点所需电流幅值，因此电机运行在J点效率最佳[1]。基于直轴电流差的MTPV控制算法能够控制电机稳定运行在J点，但是从MTPV轨迹至普通弱磁区的切换不平滑，伴随着电流和转矩震荡。

本文在超前角弱磁法[16]的基础上进行修改，提出基于电流矢量角的MTPV控制算法，利用电流矢量角实时查表得到MTPV轨迹上的电流矢量幅值，并与电流极限圆半径比较，取最小值作为电机各运行工况下的电流矢量幅值最大值，通过约束电流矢量幅值来实现MTPV控制。该算法不需要开关来完成各电流轨迹之间的切换，因此，从MTPV轨迹沿着电压极限椭圆进入普通弱磁区实现平滑切换，电流和转矩平滑过渡。

1 IPMSM数学模型

IPMSM在d-q坐标系下的电压方程为

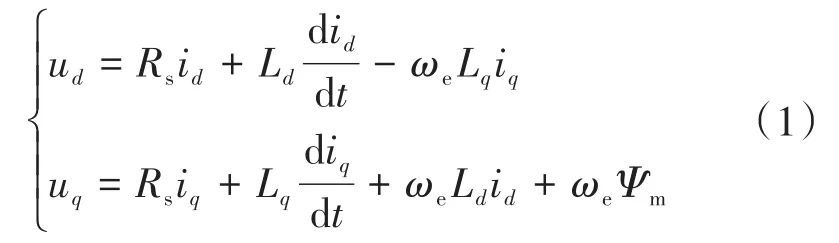
转矩方程为

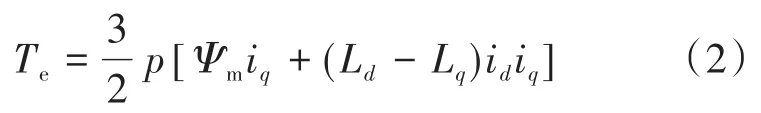
式中：ud，uq，id，iq，Ld，Lq分别为直轴和交轴电压、直轴和交轴电流、直轴和交轴电感；Rs，ωe，p，Ψm，Te分别为定子电阻、电角速度、极对数、永磁体磁链和电磁转矩。

式（2）中Te取一系列常数，在id-iq平面上可以刻画出一系列恒转矩双曲线，如图1中的T1，T2等恒转矩双曲线。

当电机处于稳态且忽略定子电阻时，电压方程修改为

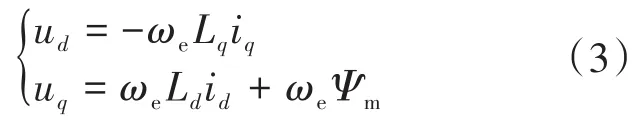
由此，电机驱动系统受到的电压限制表示为

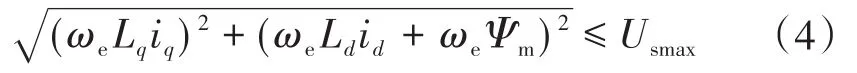
式中：Usmax为逆变器最大输出电压。

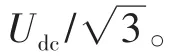
电机驱动系统受到的电流限制为

式中：Ismax为整个驱动系统能承受的最大电流，一般取为电机的额定电流。

式（5）取等号时，在id-iq平面中为圆心（0，0）的电流极限圆。

2 MTPV轨迹方程

电压极限椭圆与恒转矩曲线的切点构成了MTPV轨迹，该轨迹上的id和iq满足：

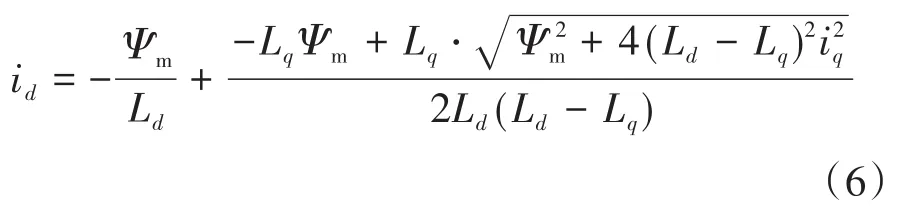
如图1中电流矢量IOG所示，电流矢量的幅值和相角与直轴电流和交轴电流之间满足：

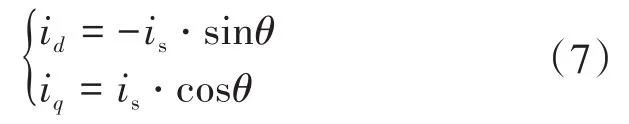
式中：is为电流矢量幅值；θ为电流矢量角。

将式（7）代入式（6），可得MTPV轨迹上的电流矢量幅值与电流矢量角之间满足：

式（8）表达式很复杂，本文采用Simulink中的Look⁃up Table模块代替公式计算，以电流矢量角作为输入，实时查表得到MTPV轨迹上的电流矢量幅值。由于查表法使用的数据表是离散的，当查表的输入值介于两个数据点之间时，可采用线性插值方法来估算输出值。因此，数据表中的数据点越多，查表输出越精确，但同时也会增加查表的工作量，导致查表时间增多，查表方法的快速性受到影响。

3 基于电流矢量角的MTPV控制算法

3.1 算法原理图

基于电流矢量角的MTPV控制算法原理图如图2所示，由Ⅰ，Ⅱ，Ⅲ等部分构成。

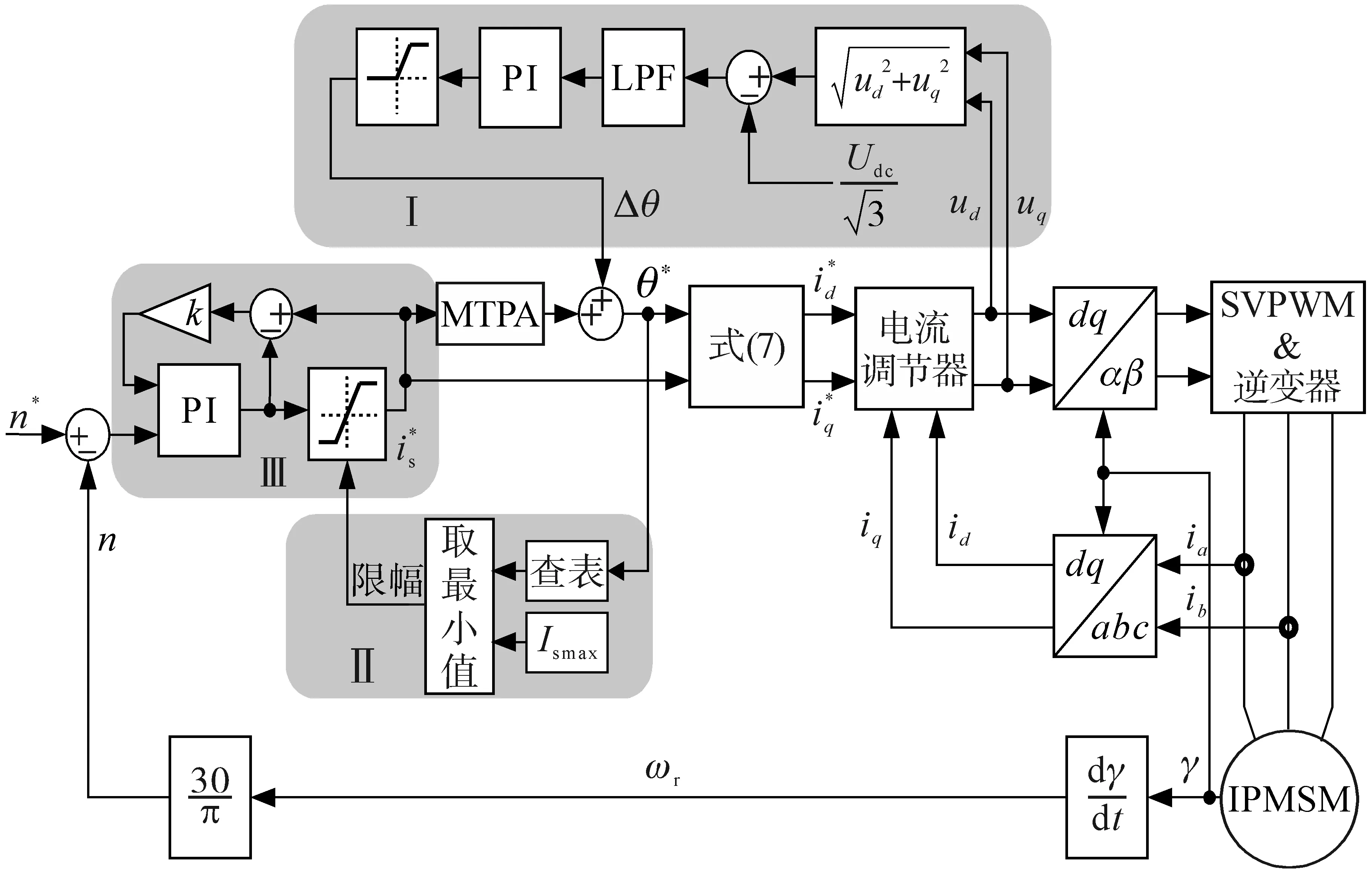
图2 基于电流矢量角的MTPV控制算法原理图Fig.2 The algorithm schematic of MTPV control based on current vector angle

Ⅰ部分使用了超前角弱磁法，利用电压差经过PI控制器生成电流矢量偏移角Δθ，使得电流矢量能够由MTPA轨迹进入弱磁区，其中使用低通滤波器（low pass filter，LPF）滤除因PWM斩波带来的高次谐波干扰。由于LPF会使被滤信号产生相位延迟，因此电流矢量偏移角也会出现延迟，导致系统动态响应性能降低。电机工作在普通弱磁区或者MTPV轨迹上，所需要的电流矢量角都能由Ⅰ部分和MTPA部分叠加生成，但由于超前角弱磁法中的电流限幅器的上限值恒为电流极限圆半径Ismax，随着弱磁程度加深，电机电流工作点就会沿着电流极限圆向下运行，导致电流工作点不能从电流极限圆进入MTPV轨迹，增加Ⅱ部分便可解决该问题。

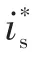
Ⅲ部分在PI控制器的基础上增加抗积分饱和功能，使PI控制器能够快速退出饱和状态[17]，实现MTPV轨迹与普通弱磁区的快速切换，有助于MTPV轨迹至普通弱磁区的平滑切换。

3.2 稳定性分析

文献[15]指出，当电机电流工作点沿着电流极限圆向下运行时，越靠近直轴，交轴电流环的增益就越大，这种巨大的增益会导致系统不稳定，出现电流和转矩震荡。随着弱磁程度加深，超前角弱磁法便会出现上述不稳定问题，如图3所示。

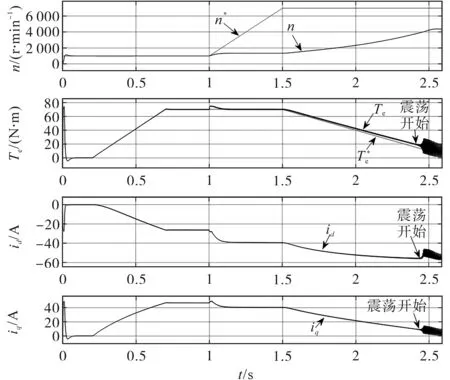
图3 超前角弱磁法运行结果Fig.3 The operation result of leading angle flux weakening method

在相同的转速和负载转矩设定下，基于电流矢量角的MTPV控制算法运行结果如图4所示，电流和转矩平稳过渡，最终稳定运行在7 000 r/min，10 N·m工况下。与超前角弱磁法相比，本文提出的改进算法控制电流工作点从电流极限圆切换至MTPV轨迹运行，一方面可以进一步扩大电机的调速范围和高速带载能力，另一方面，电流工作点沿着MTPV轨迹运行可以有效降低交轴电流环增益，系统能够稳定运行，未出现电流和转矩震荡现象。因此，本文提出的改进算法能够提高闭环系统的稳定性。

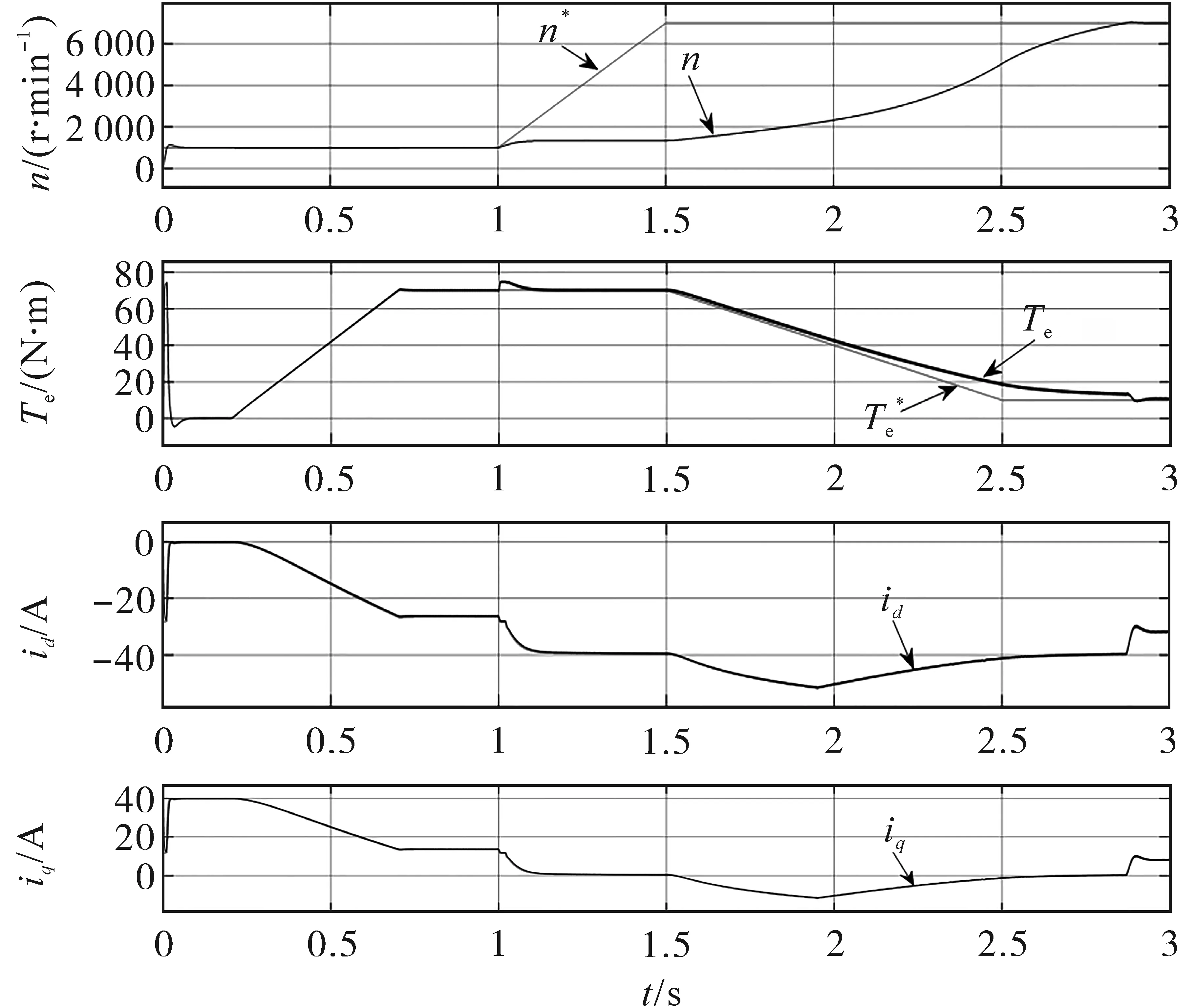
图4 改进算法运行结果Fig.4 The operation result of algorithm improved

超前角弱磁法与改进算法的实际电流轨迹如图5所示，从图中虚线方框部分可直观地发现，超前角弱磁法的实际电流轨迹在弱磁区出现了震荡现象，而改进算法的实际电流轨迹平稳运行，未发生震荡。

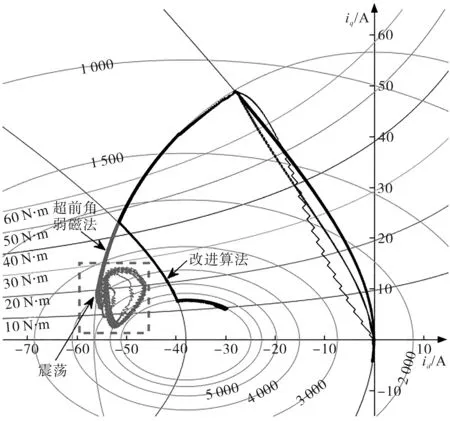
图5 实际电流轨迹对比图Fig.5 The comparison of actual current trajectories

4 仿真结果

本文采用Matlab/Simulink实现基于直轴电流差和基于电流矢量角的MTPV控制算法，对比了这两种算法控制电机电流工作点从MTPV轨迹进入普通弱磁区的切换过程，为方便描述，将基于直轴电流差的MTPV控制算法称为方法A，将基于电流矢量角的MTPV控制算法称为方法B。仿真中使用的电机参数为：极对数4，定子电阻0.085 Ω，直轴电感4.5 mH，交轴电感7.5 mH，永磁体磁链0.171 Wb，直流母线电压300 V，电机额定电流56.6 A。

电机转速和负载转矩设置如图6所示。通过设置一系列的稳态工作点，控制电机电流工作点依次沿着MTPA轨迹、60 N·m恒转矩曲线、电流极限圆、MTPV轨迹、电压极限椭圆运行，最终稳定运行在5 000 r/min，10 N·m工况下，实际电流轨迹如图7、图8所示，其中图7为方法A的实际电流轨迹，图8为方法B的实际电流轨迹。

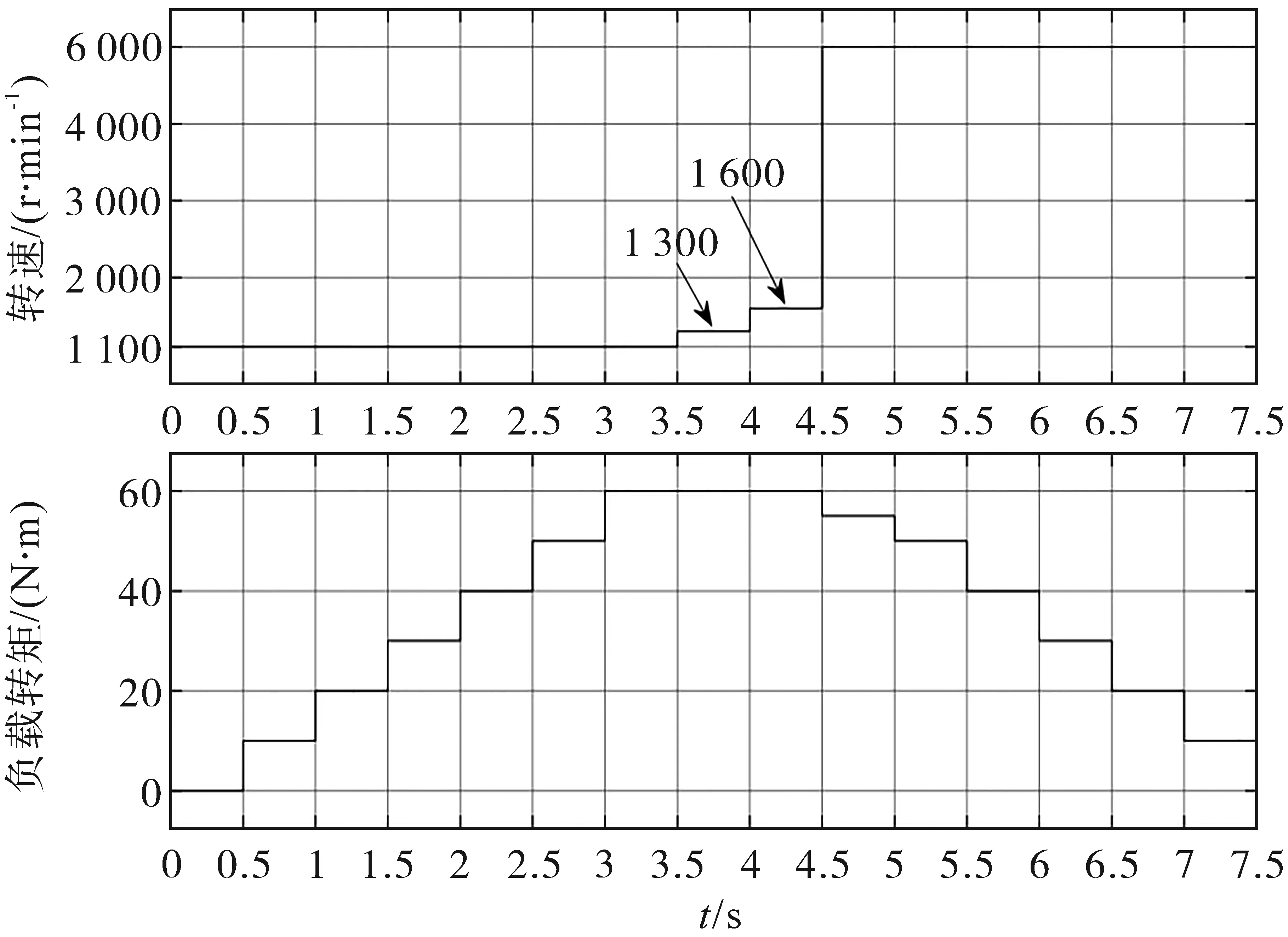
图6 电机转速和负载转矩设定值Fig.6 The setpoints of motor speed and load torque

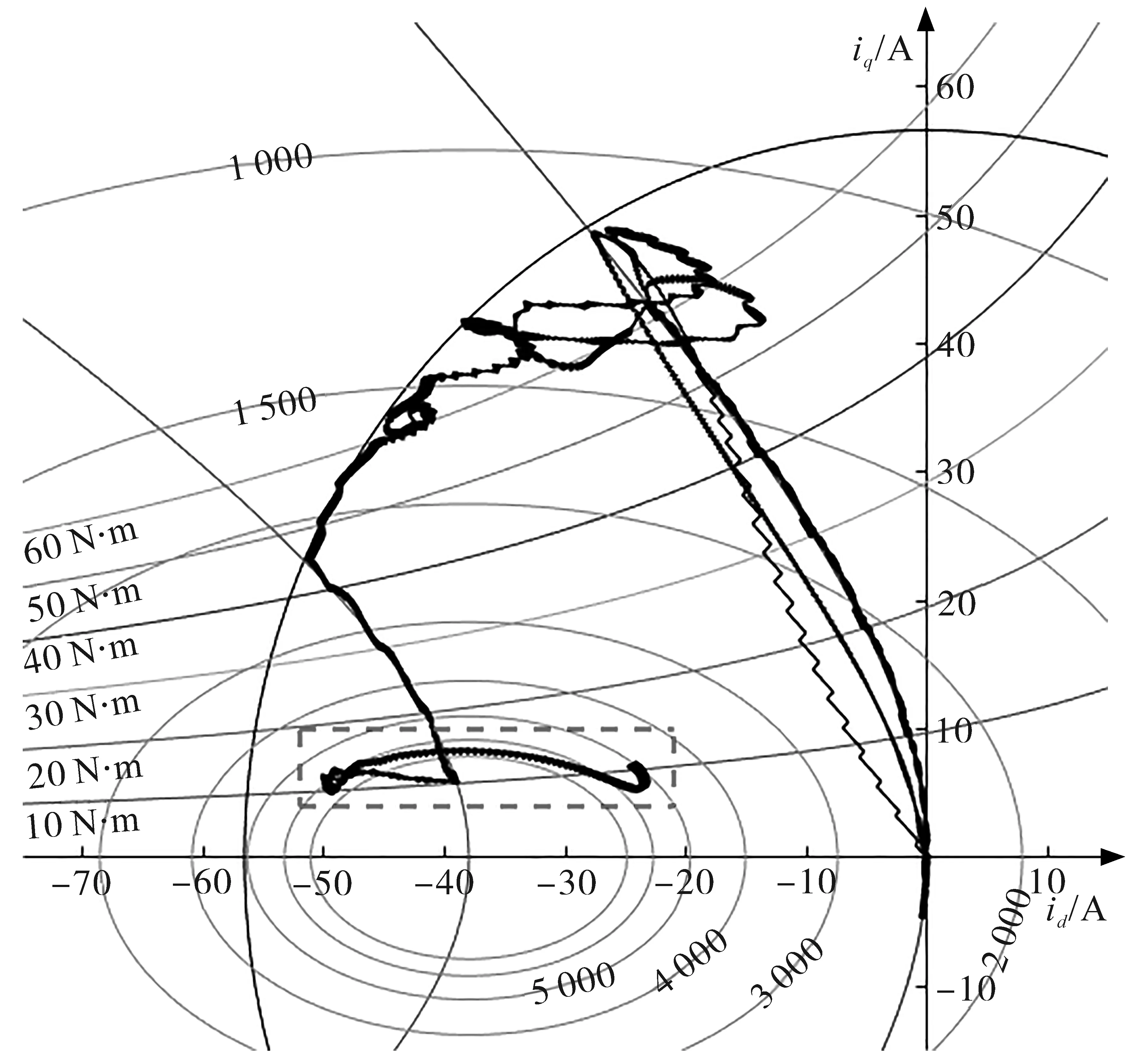
图7 方法A实际电流轨迹Fig.7 The actual current trajectory of method A

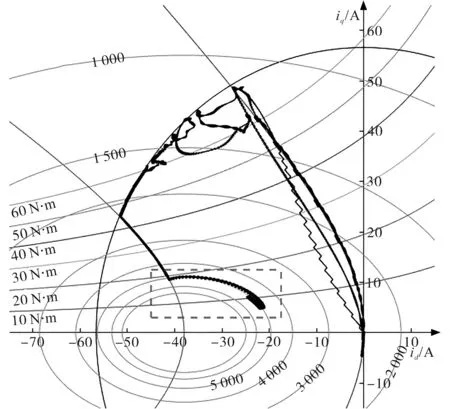
图8 方法B实际电流轨迹Fig.8 The actual current trajectory of method B

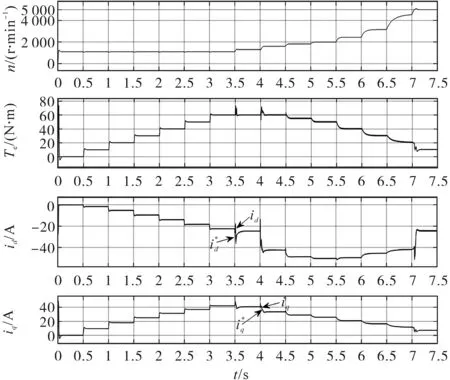
图9 方法A控制下的电机运行状态图Fig.9 Motor operating state diagram under the control of method A

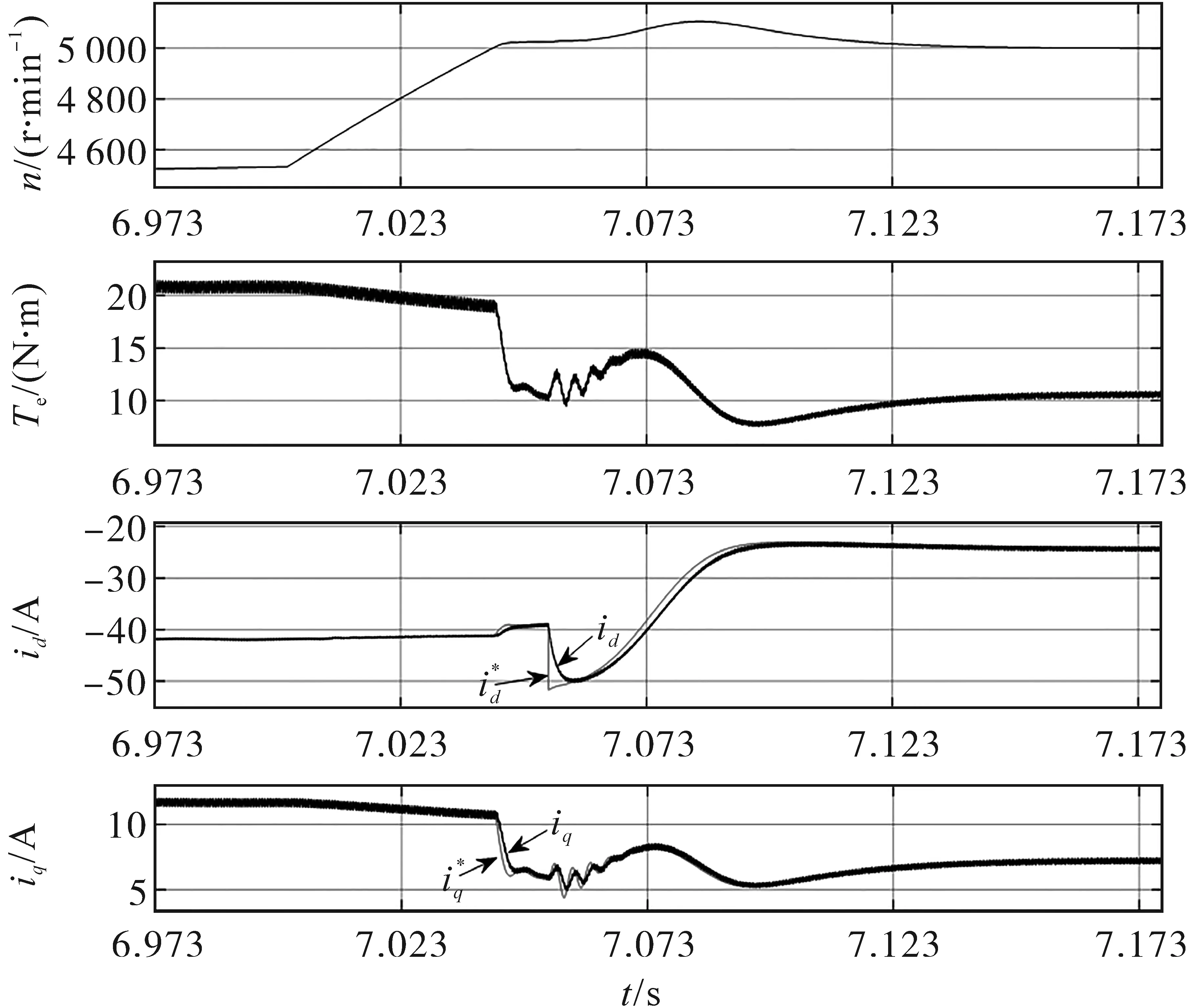
图10 方法A控制下的电流和转矩震荡Fig.10 The oscillation of current and torque under the control of method A

在方法B的控制下，电机运行状态如图11所示，从上至下依次为实际转速、电磁转矩、直轴电流、交轴电流。在第7 s左右，电机电流工作点开始从MTPV轨迹进入普通弱磁区，直轴电流、交轴电流、电磁转矩平滑过渡，未出现震荡现象，如图12所示。从图8中虚线方框部分可以直观地发现，电流轨迹平滑的从MTPV轨迹沿着电压极限椭圆切换至普通弱磁区。

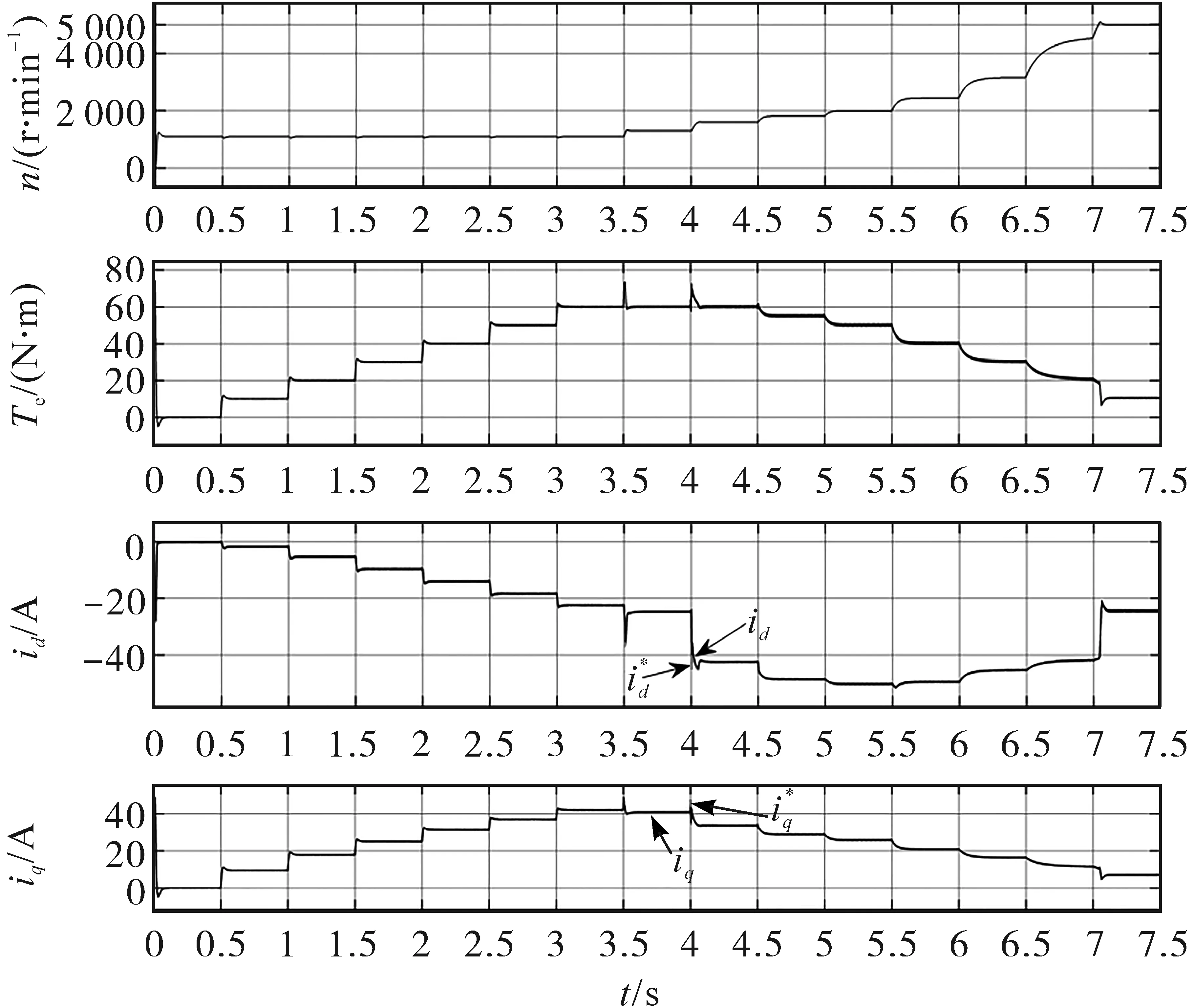
图11 方法B控制下的电机运行状态图Fig.11 Motor operating state diagram under the control of method B

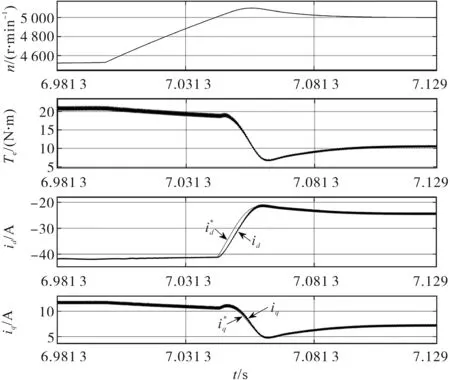
图12 方法B控制下的电流和转矩平滑过渡Fig.12 The smooth transition of current and torque under the control of method B

5 结论

本文在超前角弱磁法的基础上进行修改，提出了基于电流矢量角的MTPV控制算法，利用超前角弱磁法生成的电流矢量角能够满足MTPV控制需求这一特点，再通过约束电流矢量幅值来实现MTPV控制。通过仿真对比分析了基于直轴电流差和基于电流矢量角的MTPV控制算法，前者控制电流工作点从MTPV轨迹切换至普通弱磁区时，电流和转矩发生震荡，而后者能够实现平滑切换，因为后者不使用开关来完成MTPV轨迹与普通弱磁区之间的切换。

未来工作从优化PI控制器和改进基于直轴电流差的MTPV控制算法两个方面开展。在优化PI控制方面，通过将智能控制算法与PI控制器结合，使得控制系统能够适应所有的电机运行工况。在改进基于直轴电流差的MTPV控制算法方面，使用限幅器代替开关以便实现MTPV轨迹至普通弱磁区的平滑切换，其中取MTPV轨迹上的直轴电流值作为限幅器的下限值。