水电站预应力闸墩锚块设置次锚索参数优化数值模拟研究
王昊元
(朝阳县水务局,辽宁 朝阳 122000)
1 工程背景
赵家堡子水电站是辽宁省东部爱河流域水利开发的重要工程,坝址位于辽宁丹东凤城市石城镇境内。水电站工程主要由大坝、引水发电系统和泄洪设施组成,主要建筑物按照百年一遇洪水标准设计、千年一遇洪水标准校核。工程规划设计电站装机容量为1.68万kW,库容为1550万m3,是一座以发电为主,兼具防洪和养殖等功能的综合性中型水利工程[1]。
水库大坝为混凝土重力坝设计,其溢流坝段位于大坝右岸部位,其溢流堰为WES实用堰设计,堰顶高程为55.10m[2]。闸墩采用预应力闸墩设计,其弧形闸门的墩顶高程为80.16m,墩体厚3.0m。由于各个闸墩的尺寸和水文参数类似,因此,研究中选取具有代表性的4号闸墩进行数值模拟研究。闸墩在弧门水推力以及主锚索共同作用下,其内部的应力状态比较复杂,在垂直于主锚索的方向上会产生范围比较大的拉应力,为了减轻不利影响,可以布置一定数量的次锚索[3]。显然,不同闸墩弧门推力和主锚索的布置型式不同,将会对次锚索的设置、布置型式产生显著影响。
2 有限元计算模型
2.1 有限元模型的构建
FLUENT软件是一款比较流行的商用有限元软件包,具有丰富的物理模型、先进的数值方法和强大的前处理和后处理功能,用户主要指定初始网格和运动壁面条件,其余的网格变化均可以通过解算器自动生成。因此,此次研究选取FLUENT软件进行闸墩的有限元计算模型构建[4]。根据相关研究经验,混凝土闸墩的黏结滑移载荷往往较大,其整体位移并不会受到锚索、钢筋和混凝之间黏结滑移作用的明显影响。因此,研究中将锚索和钢筋层直接嵌入有限元模型进行计算分析[5]。为了保证研究结果的科学性和有效性,模型地基的范围沿着上下游方向分别延伸80m,溢流堰的底面向下延伸90m。构建的几何模型以顺水指向下游的方向为X轴的正方向,以竖直向上的方向为Y轴的正方向,以垂直于X轴指向右岸的方向为Z轴的正方向。由于模型的计算范围较大,采用大小不等的六面体单元进行网格划分,最终获得约312890个离散单元。闸墩坝体部的有限元模型见图1。

图1 闸墩有限元模型
2.2 算法和边界条件
鉴于溢流坝闸墩之间设置有伸缩缝结构,相邻闸墩之间的影响作用对计算结果的影响极为有限,可以忽略不计,将模型的左右边界设置为自由边界条件[6]。鉴于闸墩底部和地基的接触十分牢固,其位移变形可以忽略不计,因此,将模型的底部设计为全约束条件。在模型计算过程中,将初始增量步长设置为0.01,最大增量步设置为10000,以保证模型的计算结果的收敛[7]。计算时选择运行期的最不利工况,也就是闸墩的左侧过流,另一侧的弧形门瞬时开启,此时闸墩呈偏心受拉状态,锚索的吨位为永存吨位。
3 计算结果与分析
3.1 设置次锚索的价值分析
按照工程设计,闸墩主锚索为单侧12根布置,其中外排8根、内排4根。两排主锚索之间的间距为0.6m,外排锚索与闸墩外表面的距离为0.5m。利用上节构建的有限元计算模型,计算单根主锚索永存吨位分别为2400kN、2700kN、3000kN、3300kN、3600kN时的锚块上下游面以及内部A-A、B-B、C-C和D-D四个竖直剖面等关键部位受力规律(见表1)。由计算结果可知,在主锚索以及弧门推力的综合作用下,锚块的表面和内部会产生与主锚索方向垂直的拉应力,并且上述拉应力会随着锚索吨位的增加而增大。其中,断面B-B和断面C-C以及下游面的拉应力值明显偏大,特别是主锚索吨位为3600kN时,上述三个断面垂直于主锚索方向的拉应力值分别为1.30MPa、1.27MPa和1.51MPa,均明显大于1.0MPa,这对于闸墩的安全运行显然是不利的。

表1 不同主锚索吨位下锚块关键部位应力计算结果
为了解决锚块关键断面拉应力较大的问题,保持主锚索吨位为3600kN不变,在断面B-B和断面C-C之间,以及断面D-D和下游面之间分别布置一排单排4束的次锚索,其超张拉吨位为2100kN,永存吨位为1800kN,并对相应关键部位的应力值进行计算(见表2)。由计算结果可知,除上游面之外,锚块的受力状态明显改善,特别是垂直于主锚索方向的拉应力大幅降低,且全部小于1.0MPa。由此可见,设置次锚索对改善锚块内部应力有显著作用。

表2 设置次锚索情况下的锚块关键部位应力计算结果
3.2 次锚索数量的优化分析
在保持次锚索的位置以及超张拉吨位为2100kN、永存吨位为1800kN两个参数不变的基础上,设计无次锚索以及单排2束、单排3束以及单排4束等四种不同的次锚索数量设置方案,分别记为方案1、方案2、方案3和方案4。对上述四种方案下的锚块关键部位应力进行计算(见表3)。由计算结果可知,锚块上游面垂直于主锚索方向的拉应力值随着次锚索数量的增加而增加,但是增加的幅度相对较小,其余各个关键部位垂直于主锚索方向的拉应力值随着次锚索数量的增加而减小,但是从单排3束增加到单排4束时,其减小的幅度较为有限。综合上述分析结果和经济性要求,建议采用方案3,也就是在断面B-B和断面C-C之间,以及断面D-D和下游面之间分别布置一排单排3束的次锚索,既可以有效控制关键部位垂直于主锚索方向的拉应力值,又可以保证工程的经济性。
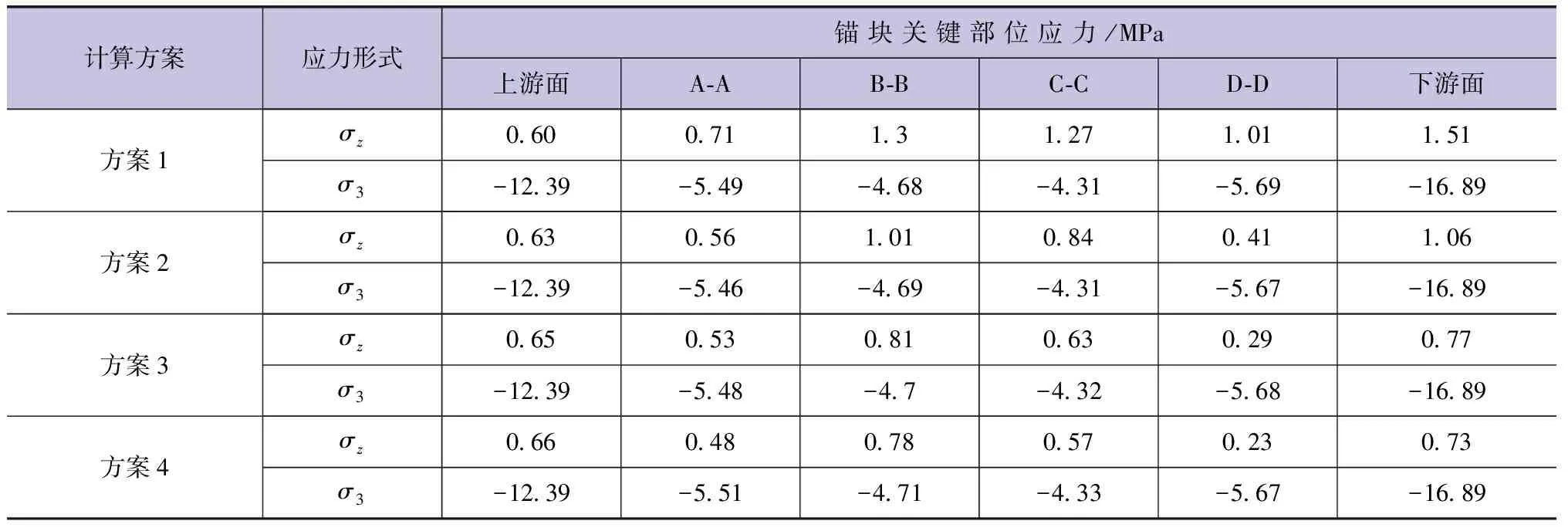
表3 不同次锚索数量下锚块关键部位应力计算结果
3.3 次锚索吨位的优化分析
为了进一步研究次锚索吨位对锚块应力的影响,设置1600kN、1800kN以及2000kN三种不同的次锚索永存吨位,分别记为方案5、方案6和方案7。利用上节构建的有限元模型,计算上述三种不同方案下的锚块关键部位应力值(见表4)。由计算结果可知,在不同次锚索吨位方案下,各个关键部位垂直于主锚索方向拉应力值的变化并没有统一的规律,其中上游面、C-C剖面以及下游面垂直于主锚索方向拉应力值随着锚索吨位的增加而增加;其余部位垂直于主锚索方向拉应力值随着锚索吨位的增加而减小。因此,结

表4 不同次锚索吨位下锚块关键部位应力计算结果
合计算结果和工程经济性,最终推荐方案6,也就是选择永存吨位1800kN的次锚索永存吨位,其超张拉吨位为永存吨位的1.167倍,也就是2100kN。
4 结 论
本文以具体工程为例,研究了预应力闸墩锚块设置次锚索的价值,并对次锚索的参数进行了优化研究,获得的主要结论如下:在主锚索以及弧门推力的综合作用下,锚块的表面和内部会产生与主锚索方向垂直的拉应力,并且上述拉应力会随着锚索吨位的增加而增大,对闸墩的安全运行不利;设置次锚索对改善锚块内部应力有显著作用,具有设置的必要性与可行性;结合受力分析结果和工程的经济性,建议在锚块的断面B-B和断面C-C之间以及断面D-D和下游面之间分别布置一排单排3束的次锚索,其永存吨位为1800kN,超张拉吨位为2100kN。

