增材制造技术中的流固耦合度影响因素

摘   要： 对流固界面的耦合程度为增材制造技术带来的挑战进行报道。以流体柱体外围绕无限远各向同性固体模型为基准，在角频率—波数域建立流体满足的声波方程、固体满足的弹性波方程和流固耦合边界条件。引入流固耦合度这一概念，导出法向位移断续、法向应力断续、切向应力为零的流固界面不完全耦合边界条件，考察不同中心频率的单极子声源在模型中激发的频散特征和波形特征。流体柱体与硬性固体相耦合，降低了各阶模式的截止频率，压制了各阶模式的传播速度，法向位移耦合度或法向应力耦合度的增大，分别使得各阶模式更加远离或靠近流体柱体外围不存在硬性固体的情形;流体柱体与软性固体相耦合，频散波仅存在一个具有较低截止频率的0阶模式，法向位移耦合度或法向应力耦合度的减小，均使得0阶模式更加远离流体柱体外围不存在软性固体的情形，且截止频率持续降低直至消失，甚至可能导致0阶模式发生反转。法向应力耦合度为零时的复杂波串并非频散曲线中的某阶模式，而是某种其他非频散波。留存于流体柱体内的“滞能纵波”和近乎于流体柱体外围绕横向各向同性固体时的传播特性，是流体柱体与软性固体相耦合时产生的特殊数学物理现象。

关键词： 增材制造;流固耦合度;角频率—波数域;流固界面不完全耦合边界条件;单极子声源;频散特征;截止频率;0阶模式;反转;非频散波;“滞能纵波”;横向各向同性

引言

声波、弹性波的传播特性，是评价增材制造工艺效果的基础指标，是检验增材制造技术制备所得物品性能的得力工具[1]。将声波、弹性波的传播特性研究贯穿于增材制造全生命周期始终，将有力推动增材制造行业精益生产，促进增材制造产品质量和竞争力提升[2]。

2017年，我国提出行动计划，明确要求提升增材制造装备、核心器件及软件质量[3]，其中数学物理方法和算法是支撑增材制造工艺智能规划、在线检测、过程控制等软件功能的核心[4]。声波、弹性波传播的数学物理研究方法涵盖理论法和数值法两种，理论法包括基于并矢格林函数的求解方法、角频率—波数域分析法等，数值法包括各时空域的有限差分法、有限元法等。文献[5]采用融合了完全匹配层全吸收边界的、适用于斜向各向同性（属于一种各向异性）介质的时域交错网格有限差分法，对弹性材料的各向异性为增材制造技术带来的挑战进行了报道，呼吁科研人员重视各向异性介质的Thomsen参数大小以及介质在各个方位的传播速度差异程度对弹性波传播特性的影响;文献[6]采用弹性波传播的并矢格林函数解，以增材制造工艺中常见的负泊松比超材料为研究对象，初步探索了超材料弹性参数线性化的普适方法，为增材制造领域共性技术创新提供了驱动力;文献[7]采用频域有限元方法，以1.5维声波、弹性波方程为例，对内在机理相对复杂、细节把控要求较高、求解具有一定技术门槛的半整数维波动方程进行了考察，尤其是对完全匹配层拉伸尺度选取、等效积分弱形式推导、流固耦合边界条件设置、极点规避等技术细节进行了注记，为更高维空间波传播特性的研究打开了局面;文献[8-9]基于声波和弹性波在流固界面的双向转换机制，推导了应用于时域有限元方法的，带有完全匹配层的声波—弹性波耦合（即流固耦合）方程的等效积分弱形式，并立足于增材制造技术应用需求，构思了若干声波—弹性波耦合模型，研讨了远场、近场条件下声波—弹性波耦合对波场传播的影响，得到了大量具有实际价值的结论和启示。文献[10]为流固耦合问题提出了一种来源于经验的传递矩阵校正方法，为流固耦合模型频散曲线的智能求取提供了便利。上述文献虽然覆盖了各维度、各时空域下基于各种数学物理方法和算法的声波、弹性波及二者之间相互耦合机制的研究，但并未考虑到声波、弹性波之间的耦合程度对波场传播的影响，而增材制造工艺的固有特点又是导致这种耦合程度的不确定性的根源所在。据此，本文引入流固耦合度这一概念，在角频率—波数域考察不同流固耦合度下波场传播的频散特征和波形特征，以期为增材制造工艺效果评价和物品制备性能检验提供更加严密、严谨的理论基础。

1  流体柱体中声波的传播

式（40）称作流固界面不完全耦合边界条件。其中，、分别称作法向位移耦合度、法向应力耦合度，处于区间[0， 1];称作切向应力耦合度，仅取0或1。当、、均为0时，式（40）退化为第1章所讨论的流体柱体中声波的传播情形;当三者均为1时，式（40）退化为第2章所讨论的流体柱体外围绕无限远固体，且流固界面完全耦合时，流体柱体内声波的传播情形;对于、（二者可以不相等）且的情形，本文将边界条件描述为：法向位移断续、法向应力断续、切向应力为零。

4  应用与讨论

4.1  模型与参数

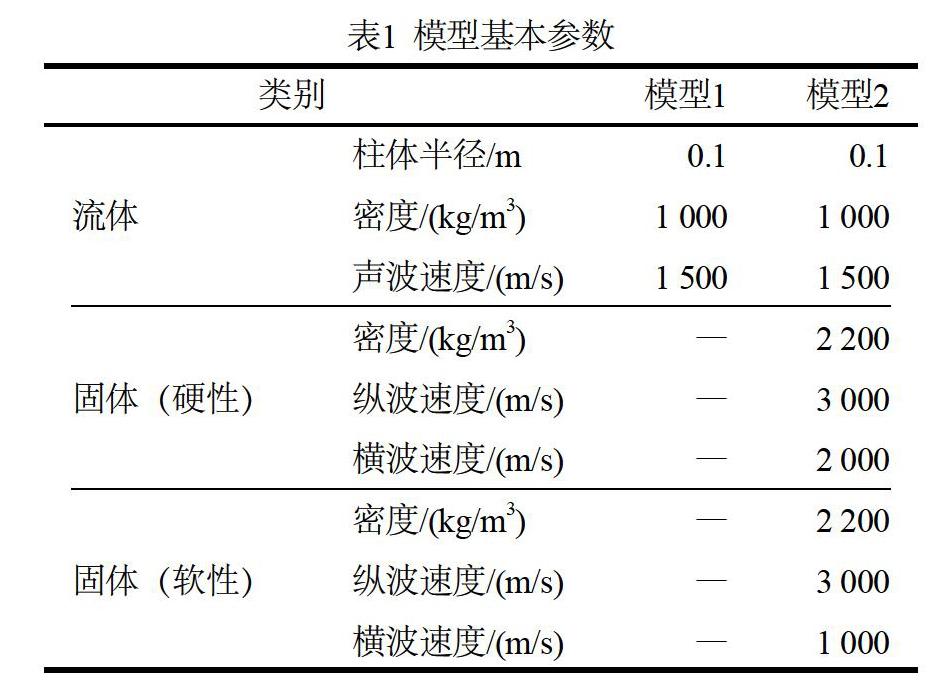
将第1章所述流体柱体的情形记作模型1，将第2章所述流体柱体外围绕无限远固体的情形记作模型2。限于篇幅，本文仅对单极子声源激发的波场进行考察。多极子声源情形的研究结论必然有所不同，但研究思路类似。

模型基本参数如表1所示，其中硬性固体指横波速度大于相邻流体中声波传播速度的固体，软性固体反之。

4.2  频散特征计算与讨论

所有满足式（46）的点集构成模型2的频散曲线。对于式（46），可根据文献[10]，首先在给定的波源频率和轴向相速度范围内对二维谱进行大体观察，判断二维谱的极性翻转特性，然后针对不同表现形式的极性翻转特性，采用校正因子实施“反翻转”，最后根据“反翻转”过程整理得到传递矩阵校正图谱，从而通过牛顿迭代法[11]求解。牛顿迭代法详见附录B。

4.2.1  流固界面完全耦合

首先，在模型2的流体柱体外围选用硬性固体，且将流固界面设定为完全耦合（即），绘制频散曲线，并与模型1相对比，如图1a所示。对比得知，在0～25 kHz频段，两个模型均具有0阶、1阶、2階模式，其中0阶模式无截止频率，其他阶模式具有较高的截止频率。此外，流体柱体与硬性固体相耦合，不仅降低了各阶模式的截止频率，而且压制了各阶模式的传播速度。在模型2中，1阶以上（含）模式在截止频率下传播速度最大，等于硬性固体的横波速度，而在模型1中，1阶以上（含）模式在截止频率下传播速度无限大（事实上，模型1的流体柱体模型是一个典型的“刚性壁”波导问题，其等效于流体柱体外围绕无限远“波速无限大的超硬性固体”的情形）。

其次，在模型2的流体柱体外围选用软性固体，仍将流固界面设定为完全耦合，绘制频散曲线，并与模型1相对比，如图1b所示。与图1a截然不同的是，模型2的频散曲线似乎与模型1毫无相关性。在0～25 kHz频段对模型2的频散曲线进行求解，仅可得到0阶模式，且该模式具有一个较低的截止频率（<1 kHz）。0阶模式在截止频率下传播速度最大，等于软性固体的横波速度。

4.2.2  流固界面不完全耦合

令人出乎意料的是，对于任意满足式（47）的流固耦合度，无论模型2采用硬性固体还是软性固体，计算得到的频散曲线均与流固界面完全耦合的情形重合。

进一步，考察法向位移耦合度、法向应力耦合度不同的情形。不失一般性，以下仅讨论0阶、1阶模式，并且为便于对比，模型1的上述模式也将在频散特征分析图中用虚线绘出。

（1）硬性固体

① 法向位移耦合度不变，法向应力耦合度变化

令不变，将分别取值为0.25、0.5、0.75、1，计算结果如图2a所示。在的不同取值下，计算结果完全相同，其中模型1和模型2的0阶模式发生了重合，1阶模式发生了交叉。与图1a对比得知，频散曲线交叉现象似乎是由模型2的1阶以上（含）模式之间相互交融而引起的。

令不变，将分别取值为0、0.25、0.5、0.75、1，计算结果如图2b所示。当时，模型2的0阶模式不存在，1阶模式在截止频率下传播速度无限大。随着的增大，模型2的0阶模式开始显现，并不断趋近于模型1的0阶模式。在的不同取值下，模型2的1阶模式近乎巧合地交于一点，当实际频率一定，且大于这一巧合交点所在的频率时，传播速度随着的增大而增大，反之亦然。初步推断这一巧合交点所在的频率为模型1的1阶模式的截止频率，该截止频率有理论解[12]，即

其中，为截止频率，为第一类变形Bessel函数的第一个虚部大于0的根[13]。将相关参数代入式（48），求得。采用牛顿迭代法在该截止频率附近对的不同取值进行精算，发现确凿如此。

分别令、、不变，取值同上，计算结果分别如图2c、2d、2e所示。除数值必然不同外，上述结果与时的规律相似，其中一个显著的区别是，当一定时， 的增大，使得模型2的0阶模式更加远离模型1。

② 法向应力耦合度不变，法向位移耦合度变化

限于篇幅，仅讨论的情形。将分别取值为0、0.25、0.5、0.75、1，计算结果如图2f所示。显而易见，当一定时，的增大，除了使得模型2的0阶模式更加远离模型1以外，也使得模型2的1阶模式更加稍微远离模型1。

（2）软性固体

章节4.2.1揭示了流体柱体外围绕无限远软性固体时频散特性的捉摸不定。因此，以下从流固耦合度由大至小开展试探性分析。

① 法向位移耦合度不变，法向应力耦合度变化

令不变，将分别取值为1、0.75、0.5、0.25、0，计算结果如图3a所示。刚减小到0.75，模型2的0阶模式的截止频率即消失;当减小到0.25时，模型2的0阶模式甚至发生了反转;当时，模型2的0阶模式不复存在。

令不变，取值同上，计算结果如图3b所示。与时不同，当减小到0.5时，模型2的0阶模式的截止频率方消失;和时的频散特性与时相似。

令不变，取值同上，计算结果如图3c所示。与以上情形不同，当减小到0.25时，模型2的0阶模式的截止频率方消失，且模型2的0阶模式未再发生反转。

令不变，取值同上，计算结果如图3d所示。在的不同取值下，模型2的0阶模式的截止频率均未消失，且模型2的0阶模式均未发生反转。此外，模型2的0阶模式对的敏感度已变得非常弱。

令不变，将分别取值为1、0.75、0.5、0.25，计算结果如图3e所示。在的不同取值下，计算结果完全相同，模型2的0阶模式频散极其轻微，且其截止频率在以上情形中最大（≈3 kHz）。

② 法向应力耦合度不变，法向位移耦合度变化

限于篇幅，仅讨论的情形。将分别取值为0.25、0.5、0.75、1，计算结果如图3f所示。显而易见，当一定时，的增大，使得模型2的0阶模式更加接近流固界面完全耦合的情形。

4.3  波形特征计算与讨论

结合章节4.2计算得到的频散特征，考察代表性中心频率3 kHz和10 kHz的单极子声源在模型1和模型2中激发的波形。声源与接收器之间的距离取1.0～2.0 m，接收器之间的间隔取0.2 m。

4.3.1  流固界面完全耦合

（1）硬性固体

绘制中心频率为3 kHz的单极子声源在模型1中激发的波形，并与其中直达波的贡献相对比，如图4a所示。在模型1中，直达波的贡献较为微弱，且衰减较快;反射波占据主要地位，为纯粹的0阶模式。进一步，绘制该声源在模型2中激发的波形，并与模型1相对比，如图4b所示。流体柱体外围硬性固体的存在，使得流体柱体内的模式波发生了迟滞，即传播速度降低，这与图1a所示的频散曲线相符合。

同理，绘制中心频率为10 kHz的单极子声源在模型1中激发的波形，并与其中直达波的贡献相对比，如图5a所示。在模型1中，直达波的贡献较为微弱，且衰减更快，但直达波与反射波的幅度比大于声源中心频率为3 kHz的情形。尽管如此，反射波依旧占据主要地位，且在一個0阶模式脉冲后有复杂波串紧随，这些波串很容易被认作1阶模式。进一步，绘制该声源在模型2中激发的波形，如图5b所示。如同章节4.2.1所提到的，流体柱体外围硬性固体的存在，压制了各阶模式的传播速度，充其量不会超过硬性固体的横波速度，这使得模式波特征得到了很大程度的简化。事实上，图5b的波串中也蕴含着多种模式，且以非频散波为主，但这已超出本文的讨论范畴，感兴趣的读者可与笔者私下讨论。

（2）软性固体

绘制中心频率为3 kHz的单极子声源在模型2中激发的波形，并与模型1相对比，如图6a所示。流体柱体外围软性固体的存在，使得流体柱体内的模式波受到了对冲，幅度严重衰减，其他模式波的幅度也远远不及流体柱体外围不存在软性固体的情形。事实上，模型2的波串中蕴含着两种模式，一是传播速度较快的，以固体纵波速度传播的非频散波，未在图1b中展示;二是传播速度较慢的，以低于固体横波速度传播的频散波，即图1b中的0阶模式。

同理，绘制中心频率为10 kHz的单极子声源在模型2中激发的波形，如图6b所示。此时，波串中仍蕴含着两种模式，一是幅度较大、传播速度较快的，以固体纵波速度传播的非频散波;二是衰减较严重的，与上述非频散波相交融的，以更加稍微低于固体横波速度传播的频散波。此外，将模型2中的波形与模型1（即图5a中实线）相对比，发现流体柱体外围绕软性固体时产生的非频散波，似乎是将流体柱体外围不存在软性固体时产生的反射波的一部分释放出去的结果，这使得留存在流体柱体内的这一部分持续了约1 ms左右即趋于平稳。部分文献将这一非频散波称作“漏能纵波”（Leaky P-wave），但按照上述分析，将留存在流体柱体内的这一部分称作“滞能纵波”（Hysteresis P-wave）似乎更为贴切。

4.3.2  流固界面不完全耦合

首先考察法向位移耦合度、法向应力耦合度相同的情形。与章节4.2.2的分析相一致，对于任意满足式（47）的流固耦合度，无论模型2采用硬性固体还是软性固体，计算得到的波形均与流固界面完全耦合的情形重合。进一步，考察法向位移耦合度、法向应力耦合度不同的情形。

（1）硬性固体

令不变，将分别取值为0.5、1，绘制中心频率为3 kHz的单极子声源激发的波形，计算结果与模型1完全相同。进一步，将单极子声源中心频率调整至10 kHz，依旧如是。

令不变，将分别取值为0、0.5、1，绘制中心频率为3 kHz的单极子声源激发的波形，计算结果对比图如图7a和7b所示。当时，复杂波串再次显现，根据图2c，3 kHz的中心频率远远小于模型2的1阶模式的截止频率，排除了这一复杂波串为1阶模式的可能，它可能是0阶模式或某种其他非频散波。随着的增大，上述复杂波串消失，此外流体柱体内的模式波传播速度相应提高，这与图2c所示的频散曲线相符合。进一步，将单极子声源中心频率调整至10 kHz，计算结果对比图如图7c和7d所示。当时，复杂波串再次显现，但由于模型2的0阶模式并不存在，进一步排除了这一复杂波串为0阶模式的可能，它只能是某种其他非频散波。与声源中心频率为3 kHz的情形相似，随着的增大，上述复杂波串消失，此外流体柱体内的模式波传播速度相应提高，这也与图2c所示的频散曲线相符合。但可意外发现，当时，波串持续时间相对更长。

令不变，将分别取值为0、0.5、1，绘制中心频率为3 kHz、10 kHz的单极子声源激发的波形，分析结论与时基本相同。限于篇幅，计算结果不再展示。

（2）软性固体

令不变，将分别取值为0.5、1，绘制中心频率为3 kHz的单极子声源激发的波形，计算结果与模型1完全相同。进一步，将单极子声源中心频率调整至10 kHz，依旧如是。

令不变，将分别取值为0、0.5、1，绘制中心频率为3 kHz的单极子声源激发的波形，计算结果对比图如图8a和8b所示。当时，复杂波串再次显现，只是比硬性固体的情形更规则有序一些，同样根据图3c，0阶模式并不存在，因此这一复杂波串只能是某种其他非频散波。随着的增大，上述复杂波串消失，此外流体柱体内的模式波传播速度相应提高，这与图3c所示的频散曲线相符合，但可以惊奇地发现，、时的模式波竟至于体现为近乎于流体柱体外围绕无限远横向各向同性（属于一种各向异性）固体时流体柱体内声波的传播特性！这极可能造成对流体柱体外围固体各向异性程度的误判。进一步，将单极子声源中心频率调整至10 kHz，计算结果对比图如图8c和8d所示。当时，复杂波串再次显现，与前文分析相同，其只能是某种其他非频散波。与声源中心频率为3 kHz的情形相似，随着的增大，上述复杂波串消失，此外流体柱体内的模式波传播速度相应提高，这也与图3c所示的频散曲线相符合，且仍可发现，当时，波串持续时间相对更长。

令不变，将分别取值为0、0.5、1，绘制中心频率為3 kHz、10 kHz的单极子声源激发的波形，分析结论与时基本相同。限于篇幅，计算结果不再展示。

5  结论与局限

本文以流体柱体外围绕无限远固体模型为基准，引入流固耦合度这一概念，在角频率—波数域考察了不同流固耦合度下波场传播的频散特征和波形特征，为增材制造工艺效果评价和物品制备性能检验提供了更加严密、严谨的理论基础。主要结论有：

（1） 流体柱体与硬性固体相耦合，不仅降低了各阶模式的截止频率，而且压制了各阶模式的传播速度。法向位移耦合度的增大，使得各阶模式更加远离流体柱体外围不存在硬性固体的情形;法向应力耦合度的增大，使得各阶模式更加靠近流体柱体外围不存在硬性固体的情形。

（2） 流体柱体与软性固体相耦合，频散波仅存在0阶模式，且该模式具有一个较低的截止频率。法向位移耦合度或法向应力耦合度的减小，均使得0阶模式更加远离流体柱体外围不存在软性固体的情形，且截止频率持续降低直至消失，甚至可能导致0阶模式发生反转。

（3） 流体柱体无论是与硬性固体还是软性固体相耦合，法向应力耦合度为0时的复杂波串均并非频散曲线中的某阶模式，而是某种其他非频散波。

（4） 留存于流体柱体内的“滞能纵波”和近乎于流体柱体外围绕横向各向同性固体时的传播特性，是流体柱体与软性固体相耦合时产生的特殊数学物理现象。

本研究尽管力求全面，但限于篇幅，仍存在一定的局限，包括但不限于：

（1） 当法向位移耦合度和法向应力耦合度相同且非零时，频散特征和波形特征并未显现出差别，表明流固耦合度的完备性有待加强;

（2） 多极子声源，如偶极子、四极子声源在流固耦合模型中的传播特性有待分析;

（3） 流体与各向异性固体相耦合时的波场传播特性有待考察;

（4） 固体—固体界面的弹性耦合度势必比流固耦合度更为复杂，有待深入;

（5） 为了有效检验由增材制造技术制备所得的更为复杂的物品的性能，流固耦合度、弹性耦合度在数值法，如各时空域的有限差分法、有限元法中的数学物理表达，有待探究。

参考文献

[1] 邵长金， 杨振清， 周广刚， 等. 场与波[M]. 东营： 中国石油大学出版社， 2015.

[2] 彼得 S. 潘迪， 罗伯特 P. 纽曼. 六西格玛管理法： 世界顶级企业追求卓越之道： 第2版[M]. 北京： 机械工业出版社， 2017.

[3] 增材制造产业发展行动计划（2017-2020年）[R].

[4] 顾樵. 数学物理方法[M]. 北京： 科学出版社， 2019.

[5] 张阔， 刘鹤. 增材制造技术中的弹性各向异性影响因素[J]. 工业技术创新， 2017， 4（4）： 53-58.

[6] 张阔. 各向同性负泊松比超材料弹性参数线性化初探[J]. 工业技术创新， 2018， 5（4）： 53-60.

[7] 张阔. 关于半整数维波动方程求解的几点注记[J]. 新一代信息技术， 2019， 2（21）： 13-21.

[8] 张阔. 增材制造技术中基于时域有限元方法的声波—弹性波耦合（一）： 理论[J]. 工业技术创新， 2019， 6（5）： 74-85， 90.

[9] 张阔. 增材制造技术中基于时域有限元方法的声波—彈性波耦合（二）： 应用[J]. 工业技术创新， 2019， 6（6）： 75-86.

[10] 张阔. 柱状模型传递矩阵校正图谱[J]. 新一代信息技术， 2020， 3（2）： 1-9.

[11] 李信真， 车刚明， 欧阳洁， 等. 计算方法： 第2版[M]. 西安： 西北工业大学出版社， 2010.

[12] 张海澜， 王秀明， 张碧星. 井孔的声场和波[M]. 北京： 科学出版社， 2004.

[13] 王元明. 数学物理方程与特殊函数[M]. 北京： 高等教育出版社， 2004.