紫外高光谱探测仪实验室辐照度定标研究

冀春延,赵敏杰,周海金,司福祺,刘建国

(1中国科学院合肥物质科学研究院安徽光学精密机械研究所,中国科学院环境光学与技术重点实验室,安徽 合肥 230031;2中国科学技术大学,安徽 合肥 230036)

0 引言

紫外高光谱探测仪在光路设计上包含地球观测光路(主光路)和太阳定标光路(定标光路),其中地球观测光路用于获取地球大气散射光光谱,太阳定标光路用于获取太阳参考谱,并经过反演得到地球大气污染物信息。因此太阳参考谱的定标精度决定了气体反演精度,需要在实验室完成定标光路的绝对辐照度定标[1,2]。

实验室辐照度定标常采用直接平行光定标法、间接平行光标定法以及直接发散光标定法[3]。美国航空航天局研制的太阳后向散射紫外探测仪(SBUV),定标时标准灯置于球面反射镜焦点,产生平行光源直接辐照仪器漫反射板,从而标定辐照度响应度,称为直接平行光定标法,该方法较难实现,并且最终引入了5.6%的绝对定标不确定度[4];中国科学院长春光学精密机械与物理研究所研制的空间紫外遥感仪器(SURSI)采用了间接平行光方式标定,氙灯位于离轴抛物面镜焦点处,产生的平行光经熔石英窗口辐照自身的漫反射板[5];欧洲航天局研制的对流层监测仪(TROPOMI)以及臭氧检测仪器(OMI)等采用直接发散光标定辐照度,选用标定后的卤钨灯直接对载荷内部的漫射板照射,实现辐照度定标[6−8]。三种方法相比,直接发散光定标引入更小的不确定度,且定标快捷容易实现。

本研究采用直接发散光标定法对紫外高光谱大气成分探测仪进行实验室辐照度定标,通过搭建定标平台对其定标光路全视场进行测量,确立了辐照度定标系数,并且对俯仰角、方位角等因素完成校正,对定标过程引入的不确定度进行了分析。

1 辐照度定标方法

紫外高光谱探测仪是基于二维面阵CCD阵列的遥感探测设备,一维用于记录太阳和大气辐射的光谱信息(光谱维),另一维用于记录辐射的空间分布信息(空间维)。图1为定标光路结构图。定标光路工作时,太阳挡板旋转一定角度,太阳光经过太阳窗口照射到安装在漫射板旋转座上的石英漫反射板或聚四氟乙烯漫反射板,经漫射板反射后,漫射光经光路切换凹面镜汇聚,依次到达望远镜次镜表面、狭缝,最终分光后进入光谱仪。

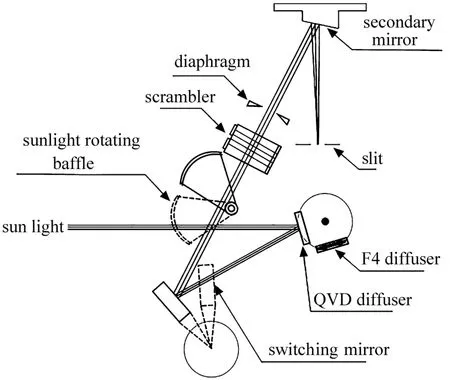
图1 定标光路结构图Fig.1 Calibration light path structure

定标光路需要在地面完成辐照度响应度定标,获得的辐照度定标系数将对日观测采集到的原始灰度值数据转化为太阳参考谱,结合主光路对地观测所获得的测量谱,借助差分吸收光谱技术(DOAS)实现对大气痕量气体的反演。采用直接发散光方式定标,紫外高光谱探测仪辐照度响应度计算公式为

式中:Ec(λ)为修正后的辐照度值;V(λ)为仪器的响应值;Ea(λ)为修正前的辐照度值;εc为辐照度修正因子,与入射角等因素有关。

搭建的辐照度定标平台如图2所示。定标装置包括高精度二维转台、1000 W标准灯、机械导轨等,紫外高光谱探测仪放置在转台中心。实验通过激光器调整光源中心与漫射板的位置:将激光器平行放置于定标灯后,激光经过定标光源中心照射在漫反射板,通过激光器和定标灯的上下调整,确保光源中心和漫射板中心高度一致。二维转台可进行水平和垂直方向的转动,其中旋转角度以图中旋转方向为正,实现定标光源不同角度的入射。定标灯放置于机械导轨上,机械导轨可通过输入参数调整定标灯与光谱仪之间的距离,来改变进入太阳窗口的辐照度。实验中调整合适的距离,保证定标灯入射光充满整个视场,使光谱仪响应具有较高的信噪比,其中定标灯到漫射板的初始距离由激光测距仪确定。平台搭建完成后采取控制变量法进行测试,采集不同角度、距离下的载荷响应以及暗背景,对数据进行分析,具体测试参数如表1所示。

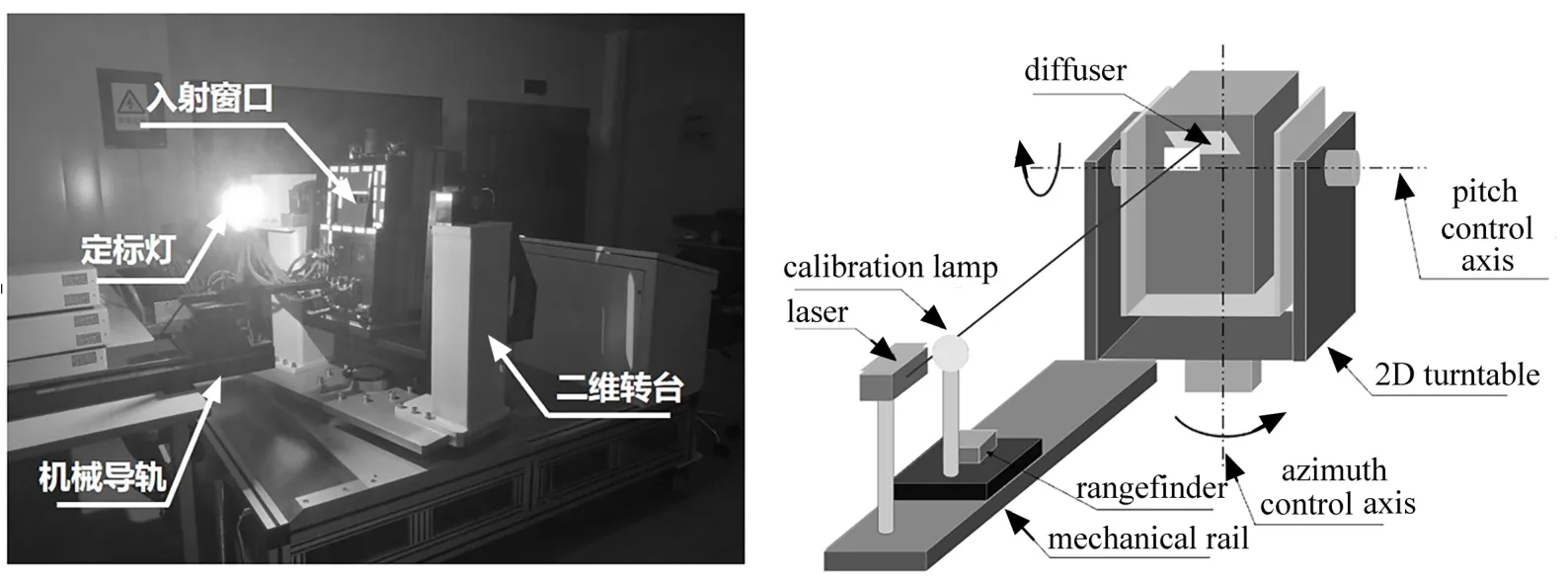
图2 辐照度定标平台Fig.2 Irradiance calibration platform

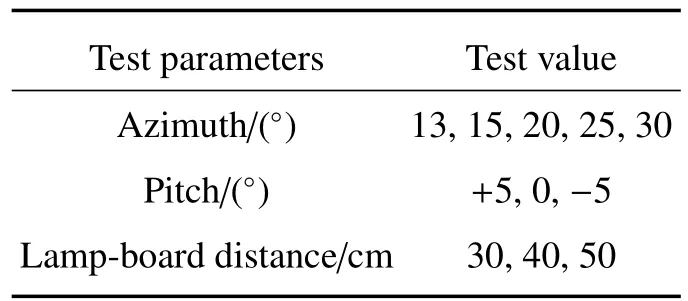
表1 辐照度定标实验测试参数Table 1 Irradiance calibration test parameters

2 辐照度定标数据及处理结果

2.1 辐照度定标数据

定标光路装配石英(QVD)漫反射板和聚四氟乙烯(F4)漫反射板,测试时通过地面测试系统切换到定标光路测试模式,并在系统中控制漫反射板的切换,根据表1的测试参数,对两板分别进行标准灯测试,实现辐照度定标,图3为QVD和F4漫射板对应的仪器采集光谱图。

图3 仪器采集光谱图。(a)石英漫反射板;(b)聚四氟乙烯漫反射板Fig.3 Instrument acquisition spectrum.(a)QVD diffuser,(b)F4 diffuser

对获得到的原始数据进行暗背景扣除,即可得到有效视场内的光谱结果,用于后续的分析计算。图4为在俯仰角0°、方位角13°、扣除暗背景后紫外2(UV2)和可见1(VIS1)通道三组入射距离30、40、50 cm下的中心视场光谱,其中入射距离均为激光测距仪测得的标准灯到漫射板中心的距离。由图可知,光谱测试结果平滑、完整。

图4 中心视场光谱。(a)UV2;(b)VIS1Fig.4 Spectrum of the central field of view.(a)UV2,(b)VIS1

2.2 辐照度的影响因素

辐照度响应与入射角度有关,包括方位角和俯仰角。直接发散光在空间辐射存在不均一性;标准灯照亮漫反射板形成面光源,随着入射角度的变化,入射光在漫反射板形成的不均一面光源发生改变,探测器的响应也随之变化。此外,辐照度响应与CCD自身的空间维和光谱维响应相关[9−13]。

实验测试中,三个入射距离为30、40、50 cm。紫外高光谱探测仪内置的QVD漫射板和F4漫射板尺寸均为横向46 mm、纵向5 mm,由于纵向宽度相对于横向宽度较窄,对于发散光源的空间分布影响较小,因此主要讨论发散光在漫射板的横向分布。在漫射板横向分布上,辐照度随着距离的增加以距离平方的反比而减小,标准灯到各点的实际距离与中心入射距离存在偏差。图5给出了实验测试的三组距离在四个方位角下的各空间维的偏差百分比示意图。由图5可知,同一方位角下对漫射板不均一性的影响随着距离的增大逐渐减小。载荷测得的太阳方位角范围由卫星的轨道参数决定,在此范围内方位角对入射光在漫射板的横向分布产生影响,使各点的偏差随着方位角的变化而改变。三个入射距离下各空间维在各方位角的偏差如图6所示,同一距离下偏差随着方位角的增大而增大。

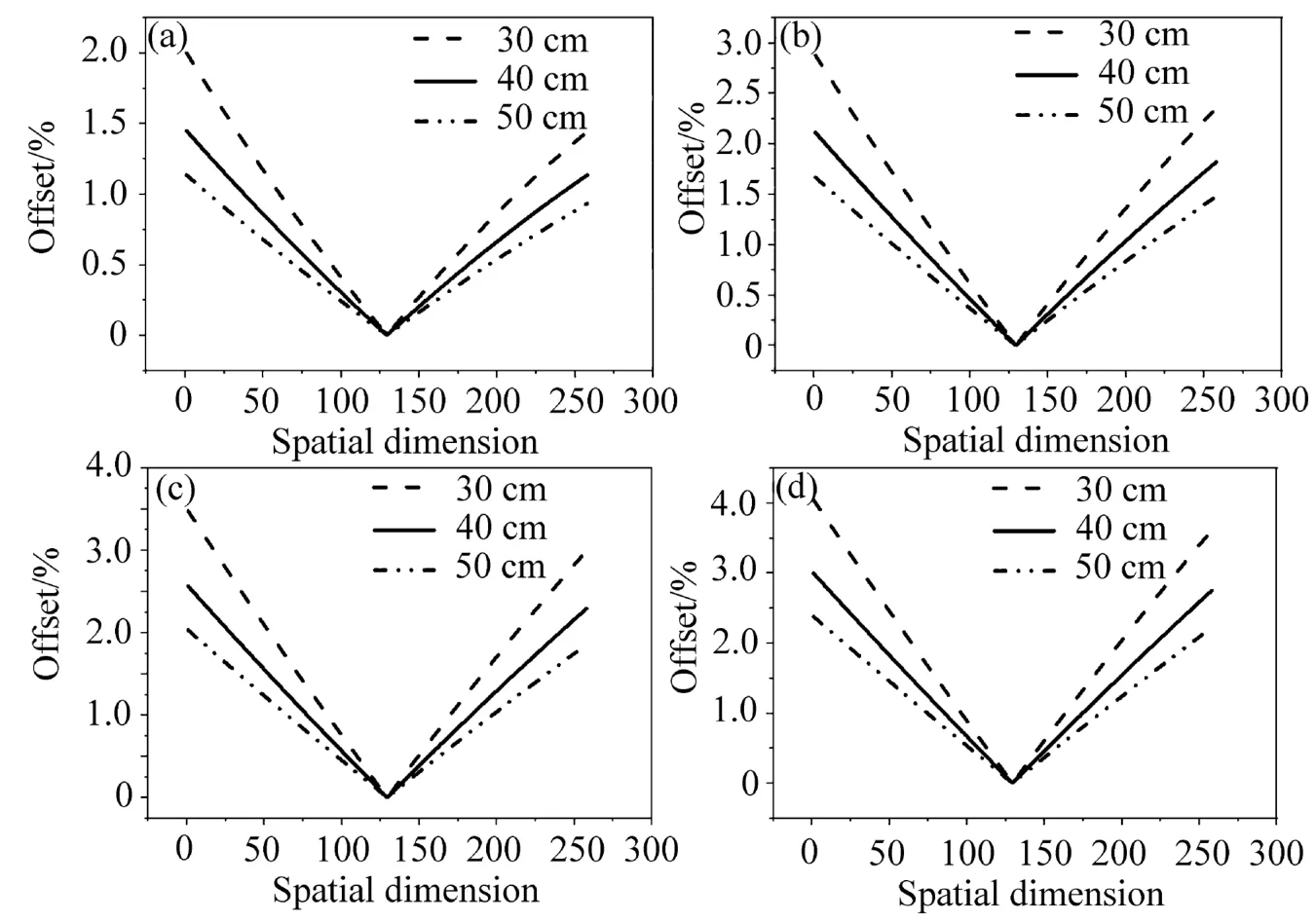
图5 四个方位角13°(a)、20°(b)、25°(c)、30°(d)下各空间维的偏差百分比Fig.5 Offset of each spatial dimension under four azimuth of 13°(a),20°(b),25°(c)and 30°(d)

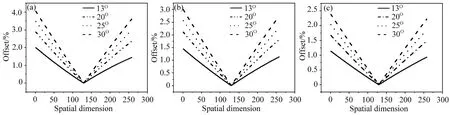
图6 三个入射距离30 cm(a)、40 cm(b)、50 cm(c)下各空间维的偏差百分比Fig.6 Offset of each spatial dimension under three distance 30 cm(a),40 cm(b)and 50 cm(c)

2.3 辐照度定标结果

将方位角因素修正后计算二维CCD上各像元点处的辐照度值,由于仪器各像元响应的差异性,需要根据各像元的光谱响应对标准灯的照度进行计算,结合标准灯到漫射板的实际距离计算响应像元点对应波长下的辐照度值。

利用美国国家标准与技术研究院(NIST)标定的特定波长下的辐照度值,采用三次样条插值法计算其他波长下的辐照度。三次样条插值法计算结果稳定、收敛性好,插值结果具有较高的光滑度[14,15]。以空间维100行为例,图7为对实验距离50 cm、方位角13°下校正后的UV2、VIS1、VIS2三个通道下的照度值,其中三角符号表示NIST给定的50 cm处的照度值。

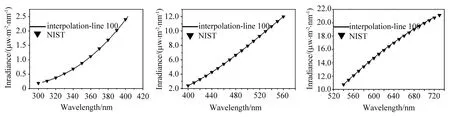
图7 NIST标定的辐照度与校正后的插值结果对比。(a)紫外2;(b)可见1;(c)可见2Fig.7 Comparison of NIST-calibrated irradiance and corrected interpolation results.(a)UV2,(b)VIS1,(c)VIS2

2.4 辐照度定标系数计算

对二维CCD探测器的每一个像元点计算修正后的三个距离30、40、50 cm处的照度值。用数组[Xl,i,j,Yl,i,j]表示响应值与辐照度值组合,Xl,i,j代表不同距离下的像元响应值,Yl,i,j为修正后的辐照度插值结果,下标l表示为三个实验距离,i代表行号,即空间维像元号,j代表列号,为光谱维像元号。建立辐照度定标模型,采用最小二乘法对数据线性回归分析求解辐照度定标系数a、b,其计算公式为

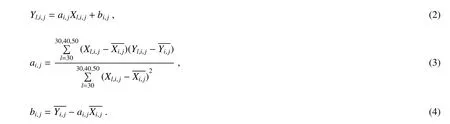
选择俯仰角5°、方位角20°下空间维85维、波长396.516 nm处的像元点为例,给出了UV2通道下对卤钨灯的线性回归结果,定标方程为

三个通道下的辐照度定标系数a、b在空间维100维、俯仰角5°、方位角20°的有效视场内的结果如图8所示。

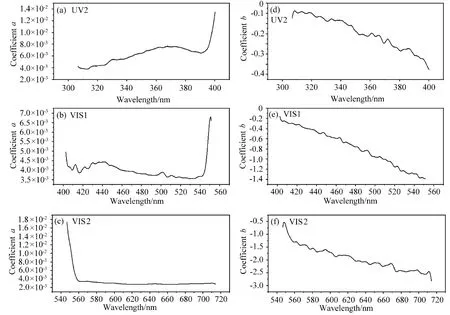
图8 三个通道UV2、VIS1、VIS2下的辐照度定标系数a(a)-(c)、b(d)-(f)Fig.8 Irradiance calibration coefficient results of three channels a(a)-(c)and b(d)-(f)

3 不确定度分析

紫外高光谱探测仪对于辐照度定标过程中的偏差要求为小于5%,通过分析紫外高光谱探测仪的辐照度定标过程,发现影响其定标精度的因素主要来自于定标灯的不稳定性、转台精度误差、仪器响应非稳定性、光谱定标不确定度以及回归计算误差。具体不确定度的主要来源分析如下:

1)定标灯的辐照度不确定度:1000 W卤钨灯辐照度由NIST标定,定标过程的不确定度由证书给出,由于不同波长处的不确定度存在差异,通过平均处理确定每个通道下的不确定度,如紫外2通道下平均不确定度为2.5%。

2)实验选用的二维转台由实验室自主制造,其机械定位精度为0.01°,转台不确定度将会传递到辐照度修正中。

3)实验过程中对同一测试条件下的标准光源采集了多组数据,设置CCD积分时间为0.4 s,连续采集100组数据,对采集的数据进行均值处理,计算各组数据的标准差,得到仪器的响应非稳定性不确定度。非稳定性不确定度δc的计算公式为:

式中:n为测试组数,DNi为第i次的测量数据,为测试期间的平均值,根据上式分别计算各角度的非稳定不确定度,对于同一通道下的计算结果,各角度下的不确定度偏差在±0.2%以内。

4)回归计算不确定度在辐照度定标系数计算过程中引入,由最小二乘法回归分析引起。由回归直线与标准值之差决定,采用残差标准差来计算每个像元点不确定度,通过对每一个通道各个像元点的不确定度均值计算得到线性回归不确定度。

对于以上不确定度进行合成,合成不确定度由各不确定度平方和开方得到,即误差传递公式

式中:δa为定标灯不确定度,δb为二维转台不确定度,δc为仪器响应非稳定性不确定度,δd为线性回归不确定度。各通道不确定度分析如表2所示。

表2 不确定度结果Table 2 Uncertainty results

4 结论

研究了紫外高光谱探测仪的辐照度定标技术。根据紫外高光谱探测仪的定标结构特点,选择了直接发散光定标方法,相应建立了定标平台,对不同的角度、距离进行了多组测试,通过线性回归分析计算其辐照度定标方程,获得了辐照度定标系数,同时完成了对方位角等因素的校正。分析讨论了整个实验过程中的各不确定度来源,最终计算得到的合成不确定度满足定标精度要求(5%以下)。辐照度定标工作的完成为紫外高光谱探测仪的应用提供了数据支持,不确定度分析为数据的可靠性提供了保障,辐照度定标系数对于后续的在轨测试、太阳参考谱获取等工作建立了工作基础。