Shadowing Homoclinic Chains to a Symplectic Critical Manifold

Sergey Bolotin

Moscow Steklov Mathematical Institute,Russian Academy of Sciences,Moscow,119991,Russia

Abstract.We prove the existence of trajectories shadowing chains of heteroclinic orbits to a symplectic normally hyperbolic critical manifold of a Hamiltonian system.The results are quite different for real and complex eigenvalues.General results are applied to Hamiltonian systems depending on a parameter which slowly changes with rateε.If the frozen autonomous system has a hyperbolic equilibrium possessing transverse homoclinic orbits,we construct trajectories shadowing homoclinic chains with energy having quasirandom jumps of orderεand changing with average rate of order ε|lnε|.This provides a partial multidimensional extension of the results of A.Neishtadt on the destruction of adiabatic invariants for systems with one degree of freedom and a figure 8 separatrix.

Key Words:Hamiltonian system,homoclinic orbit,shadowing.

1 Introduction

Consider a smooth Hamiltonian system(M,ω,H)with phase space M,symplectic form ωand Hamiltonian H.Let v=J∇H be the Hamiltonian vector field andφthe phase flow.Suppose H has a connected symplectic nondegenerate critical manifold N.Then any z∈N is a critical point of H with rank dH(z)=dim M−dim N,and the restriction ω|is nondegenerate.We also assume that N is normally hyperbolic,i.e.,nonzero eigenvalues of the linearizationΛ(z)=Dv(z)have nonzero real parts.Denote by

E={ξ∈TM:ω(ξ,η)=0 for allη∈TN}the symplectic complement to TN.Since N is symplectic,TM=TN⊕Eandω|is nondegenerate.Hence E=E⊕E,where EareΛ(z)-invariant Lagrangian stable and unstable subspaces of Ecorresponding to the eigenvalues with negative and positive real parts respectively.

Let

be the stable and unstable manifolds of z∈N and

W(N)=∪W(z)

the stable and unstable manifolds of N.The intersection W(N)∩W(N)N consists of orbitsγ:R→M homoclinic to N,i.e.,heteroclinic from z=γ(−∞)to z=γ(+∞).The heteroclinic orbit is called transverse if TW(z)∩TW(N)=R˙γ(t).

Define a multivalued partially defined symplectic scattering map F:N→N by F(z)=zif there is a transverse heteroclinic from zto z.We call a sequenceσ=(σ)of transverse heteroclinic orbits a heteroclinic chain ifσ(+∞)=σ(−∞)=z∈N.A heteroclinic chain corresponds to an orbit z=(z)of the scattering map.We call the chain strongly nondegenerate if the orbit z is hyperbolic.

Without loss of generality let N⊂Σ=H(0).Our goal is to construct,for smallµ,orbitsγ:R→Σ=H(µ)shadowing strongly nondegenerate infinite heteroclinic chains.This requires several assumptions which are different for real and complex eigenvalues.For degenerate heteroclinic chains we get weaker results.

Our research is motivated by two classical problems.The first is Poincar´e’s theory of second species almost collision solutions in celestial mechanics.This application was already discussed in[6,7],so we will be brief.Consider the plane 3 body problem with two small masses of orderµ≪1.Let the center of mass be at rest and let qbe the relative positions of small bodies with respect to the large one.Then we obtain the Hamiltonian

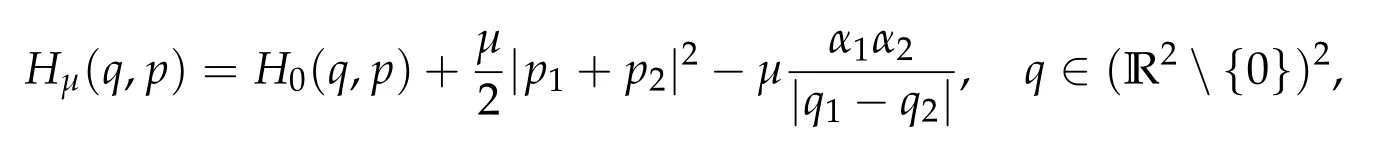
where

In the second application also complex eigenvalues may appear.Consider a slowly time dependent Hamiltonian system on a symplectic manifold M:

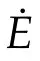
is an adiabatic invariant[1].For smallεthe change of I(t)=I(τ(t),E(t))on long time intervals is small:

Then the energy changes gradually:(τ,E)approximately follow a level curve I(τ,E)=const.

However,(1.2)fails for trajectories passing near equilibria,since then the frozen dynamics is slow,and the averaging method does not work.A.Neishtadt[19]considered the case when the plane frozen system has a hyperbolic equilibrium with a figure 8 separatrix–union of two homoclinic loops.The separatrix divides the plane in 3 regions.In the interior of each region there is an adiabatic invariant,so(τ,E)follows its level curves.Neishtadt showed that when a trajectory crosses the separatrix,the adiabatic invariant,and hence also the energy,have jumps of orderε.Then large measure of trajectories have quasirandom behavior,and the energy changes with average speed of orderε|lnε|.

Let us show how to reduce the problem to a general theorem on shadowing heteroclinic chains to a normally hyperbolic symplectic critical manifold.For simplicity suppose that H(z,τ)is periodic inτ∈T.Replacing H by H−H(z(τ),τ)we may assume that

Consider an autonomous Hamiltonian system

and symplectic structure

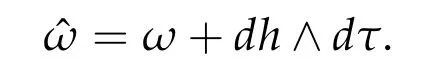
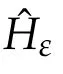
and homoclinics of the frozen system define families of homoclinics to the manifold N.

The shadowing theorems we prove have roots in many classical results in dynamical systems and calculus of variations which are too numerous to mention.Maybe the most important for us were the Turayev–Shilnikov theorem[23]and the works of P.Rabinowitz[12],E.Sere[21]and many others on the existence of multibump homoclinics by variational methods.Some ideas used in this paper were developed over the years in collaboration with Paul Rabinowitz.In particular[8]was a foundation to the present research.However we do not use global variational methods as in[8],since transversality of heteroclinics is assumed.

Phenomena similar to the ones studied in this paper appear in the problem of Arnold’s diffusion for nearly integrable Hamiltonian systems near a multiple resonance[2,11,14,20,26].Our research is also closely related to the theory of scattering maps[13]and of separatrix maps[25].

In this paper we use local variational methods,more precisely generating functions of symplectic relations and discrete action functionals.For Tonelli Hamiltonians one can use global methods of Aubry–Mather theory[2,11,20].However for general Hamiltonians considered in this paper only local variational methods work.

Next we formulate and prove general shadowing theorems for systems with a normally hyperbolic symplectic critical manifold.In the last section these results are applied to slowly time dependent systems.

2 Main results

Let Nbe a connected symplectic normally hyperbolic critical manifold of a Hamiltonian system(M,ω,H).We assume N⊂Σ=H(0).Define projectionsπ:W(N)→N byπ(x)=z if x∈W(z):

Following[13],define a scattering relation R⊂N×N setting(z,z)∈R if there is an orbit heteroclinic from zto z,i.e.,there is a∈W(N)∩W(N)N such that π(a)=z.If R is locally a graph,then it defines a branch of the symplectic scattering map F:N→N.The general theory of scattering maps was developed in[13].However,our case is different because the manifold N is critical and the energy levelΣcontaining N is not a manifold,so the results in[13]do not apply directly.

If a heteroclinic orbitγ(t)=φ(a),γ(±∞)=c∈N is transverse,then the following equivalent conditions hold.Let v be the Hamiltonian vector field.

•TW(c)∩TW(N)=R v(a).

•TW(c)∩TW(N)=R v(a).

•The symplectic formωdefines a nondegenerate modulo R v(a)bilinear form on TW(c)×TW(c).

TW(L)∩TW(L)=R v(a).

Then the scattering map F has a well defined smooth branch f:V→V,where V⊂N are neighborhoods of c.Let(x,y)∈Rbe local symplectic coordinates in Vsuch thatω|=d y∧d xand

L={y=b}=B×{b}, L={x=a}={a}×B,

where c=(a,b)and Bare small balls in Rcentered at aand brespectively. Then for(x,y)in a neighborhood of(a,b),the Lagrangian manifolds W({x}×B)and W(B×{y})intersect transversely inΣalong a heteroclinic trajectoryσ(x,y)joining the points z=(x,y)with f(z)=z=(x,y).We represent f by a generating function S(x,y):

Although the functional is formal,its derivative is a well defined sequence in l(R).It is well known that the orbit z is hyperbolic(has nonzero Lyapunov exponents)iff the Hessian A(z)has a bounded inverse in l.Then we call the chainσ=(σ)strongly nondegenerate.To shadow the chainσby a trajectory onΣ=H(µ)with smallµ/=0,we need more conditions.

LetΛ(z)=Dv(z)andΛ(z)=Λ|.Let

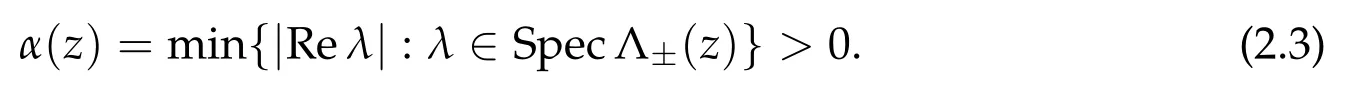
Then

We call an eigenvalueλofΛ(z)leading if|Reλ|=α(z).Generically leading eigenvalues are simple.Then there are 2 cases:

•Real case:±α(z)are real simple leading eigenvalues.

•Complex case:±α(z)±iβ(z),β(z)>0,are complex simple leading eigenvalues.

We assume that one of the cases hold for all z∈N.

The results in the real and complex case are different.The real case was studied in[7]under the assumption that the eigenvalues have maximal multiplicity.For N a single hyperbolic equilibrium with real eigenvalues the result was discovered much earlier by Turayev and Shilnikov[23],and the proofs(with different generality)were given in[8,24].For N a hyperbolic equilibrium with complex eigenvalues of a system with two degrees of freedom the problem was studied by Devaney[15].In[10],variational methods were used to extend the results of[15]to the case of nontransverse homoclinics.

First consider the real case.Then the flow on W(z)looks like a node:for any a∈W(z)there exist the limits

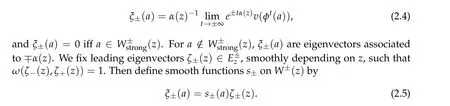
H(z,q,p)=−α(z)pq+O(p,···,p,q,···,q)+O(p,q),

we have s=−q+O(q)and s=p+O(p).

For a leading heteroclinic orbitγset

Note thatρ(γ)does not depend on the choice of the pointγ(0)onγ(R).

Letσ=(σ)be a leading heteroclinic chain corresponding to an orbit(c)of the scattering map.We callσpositive(negative)if

ρ(σ)ρ(σ)>0, (ρ(σ)ρ(σ)<0) for all i.

Positive heteroclinic chains can be shadowed by orbits with small positive energy,and negative chains with small negative energy.

Theorem 2.1.Suppose leading eigenvalues are real and simple.There isµ>0 such that for anyµ∈(0,µ]and any strongly nondegenerate positive heteroclinic chainσ=(σ)there exists an orbitγ:R→Σshadowing the chainσ.More precisely:

π(γ(t))shadows the orbit(c)of the scattering map:d(c,z)≤Cµ|lnµ|.

If the chainσis negative,then shadowing orbits exist onΣwithµ∈[−µ,0).If the chain is not positive or negative,then in general there are no shadowing orbits satisfying conditions in the theorem.

Theorem 2.1 is a generalization of the main result in[7].In[7]it is assumed that Λ(z)=∓α(z)I,and only periodic heteroclinic chains were considered.

For complex leading eigenvalues there are more shadowing trajectories.

C is a constant independent ofµand the chainσ.

Theorem 2.2.Suppose the leading eigenvalues are simple and complex.For any integer mthere existsµ>0 such that for any strongly nondegenerate leading heteroclinic chainσ=(σ),any integer sequence 0≤n≤m,and anyµ∈[−µ,µ]{0},

Remark 2.2.In the complex case there exist also shadowing orbits onΣ,including multibump homoclinic orbits.For two degrees of freedom and N a single equilibrium this was proved in[10].However we will not discuss this result since it does not apply to slowly time dependent systems.

It follows from the proof that the orbits in Theorems 2.1 and 2.2 are hyperbolic with nonzero Lyapunov exponents.Sinceµis independent of the chain,if F has a compact hyperbolic invariant set,then shadowing orbits form a compact hyperbolic invariant set inΣ.If the heteroclinic chain(and the sequence(n)in Theorem 2.2)are periodic,then the shadowing orbits will be periodic.

Unfortunately in our application to slowly time dependent systems the heteroclinic chains are degenerate.So we need weaker results for finite homoclinic chains.

In particular,

In the complex case we have

In particular,by(2.8),

The proofs of Theorems 2.3 and 2.4 are simplified versions of the proofs of Theorems 2.1 and 2.2,so we skip them.These theorems work for finite chains with n independent ofµ.But then one can continue the procedure using a version of the continuation lemma,see[25,26]and[17].The details will be published in another paper.

3 Proofs of the shadowing theorems

3.1 Generating functions of local symplectic relations

First we describe trajectories passing close to the critical manifold N.Take a small domain V⊂N with symplectic coordinates z=(x,y)and identify V with a domain in R.If V is small enough,a tubular neighborhood U of V in M can be identified with

in such a way that

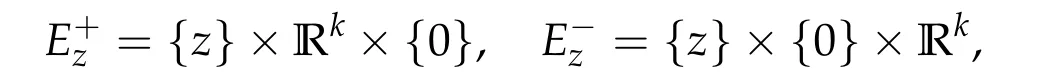
and the coordinates in U are symplectic:

ω|=d y∧d x+d p∧d q, z=(x,y)∈V.

Then

where

g=O(q), g=O(p), h=O(q), h=O(p).

They can be also represented by generating functions.

Proposition 3.1.There exist smooth functions

on open sets in R×R×Rsuch that for any z= (x,y) ∈ V and A=(x,y,q,p)∈U,

Equivalently,

Define a symplectic relation L⊂U×U as follows:(A,A)∈L if there exists z∈V such that A∈W(z).The relation is represented by the generating function

F(z,Z)=S(y,x,q)+S(x,y,p)−〈x,y〉, Z=(x,y,q,p),via the equations

Let

L(Z)=CritF(z,Z)=F(ζ(Z),Z),

which means taking the critical value at the nondegenerate critical point z=ζ(Z)with respect to z.We obtain

Proposition 3.2.The generating function L defines the symplectic relation(A,A)∈L by the equations

d L(Z)=yd x+xd y+pd q+qd p.

From now on we assume that r>0 is small enough.The next proposition is a minor generalization of Shilnikov’s theorem[22],orλ-lemma.The proof is an application of the contraction principle,see[7,16].

Proposition 3.3.For any(z,q,p)∈V×B×Band T≥1:

•There exists a unique solutionγ:[−T,T]→U,

satisfying the initial–boundary conditions

•γsmoothly depends on z,q,p,T.

•Letγ(∓T)=A=(z,q,p).Then

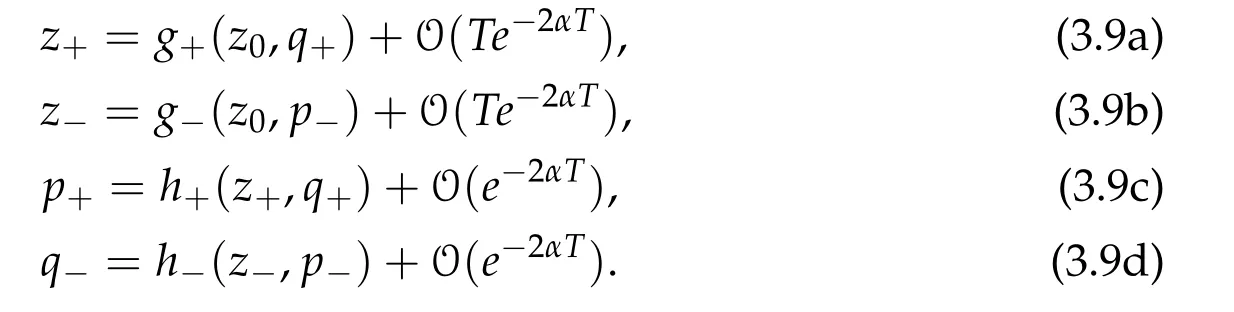
We write for simplicityα=α(z).Let

If Z=(x,q,y,p)is given,we can solve Eqs.(3.9a)–(3.9b)for z=ζ(Z)+O(Te).

Then we obtain a symplectic relation(A,A)∈Lif the points are joined by a trajectoryγ:[−T,T]→U.The relation Lis defined by the generating function

L(Z)=L(Z)+O(Te).

To construct trajectories with given energy we need to find H(γ(0))for the trajectory γin Proposition 3.3.Up to now it did not matter if the leading eigenvalues were real or complex.Now we have to consider these cases separately.

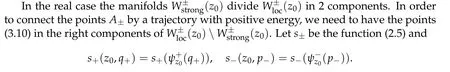
H(γ(0))=αes(z,q)s(z,p)+O(e), ν>0.

LetΩbe a compact set contained in

{(z,q,p)∈V×B×B:s(z,q)s(z,,p)>0}.

Later on we takeΩ=V×Q×P,where P,Q⊂BBare small closed balls.Letµ>0 be small enough andµ∈(0,µ].Solving the equation H(γ(0))=µfor T we obtain:

Proposition 3.4.For anyµ∈(0,µ]and(z,q,p)∈Ω:

•There exist

and a unique solution(3.7)onΣ∩U satisfying(3.8).

•γand T smoothly depend on z,q,p,µ.

•γconverges to the concatenationγ·γasµ→0.

•The boundary points Aofγsatisfy d(A,B)≤Cµ|lnµ|.

Proposition 3.4 was proved in[7]for equal real eigenvalues.In[16]the proof was extended to the generic real case.

We have a symplectic relation:(A,A)∈Lif there exists zsuch that the points Aare joined by a trajectory in Proposition 3.4.The generating function of the relation is

where L is the generating function in Proposition 3.2.

Lemma 3.1.We have whereν>0 and f,g are linear functions such that

The proof is a computation similar to the one in[10].LetΛ=Λ(z).We have

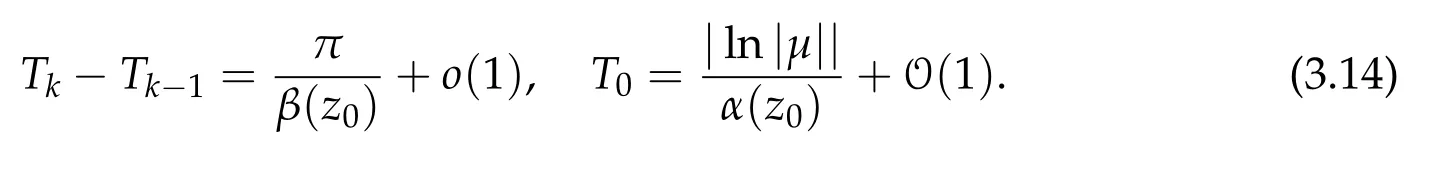
We obtain:

Proposition 3.5.For any integer mthere existsµ>0 such that forµ∈[−µ,µ]{0}and any(z,q,p)∈Ω:

•γand Tsmoothly depend on z,q,p,µ.

•γconverges to the concatenationγ·γasµ→0.

Without restricting toΩwe get a multivaluedψ.

•The boundary points satisfy d(A,B)≤Cµ|lnµ|.

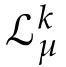
The following corollary works both for real and complex cases.Let the sets P and Q be chosen as above.In the complex case we fix an integer k∈[0,m]and drop the dependence on k from the notation.Letµ∈(0,µ]in the real case,andµ∈[−µ,0)∪(0,µ]in the complex case.Let F be the generating function in(3.6).

Corollary 3.1.The symplectic relation Lis given by the generating function

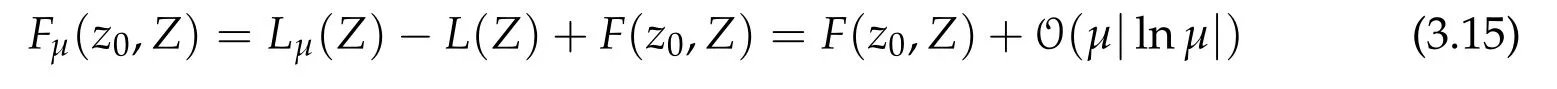
via the equations

3.2 Discrete variational problem

To formulate a variational problem for shadowing orbits we need to relate the generating functions of the stable and unstable manifolds W(N)and of the scattering map F.

Let f:V→Vbe a local branch of F represented by a generating function S as in(2.1).Then to any(x,y)in a small open set W⊂Rthere corresponds the transverse heteroclinicσ(x,y)joining z=(x,y)∈Vwith z=f(z)=(x,y)∈V.As in(3.1),let(x,y,q,p)be symplectic coordinates in a neighborhood

Let A(x,y)∈Ube the first intersection point ofσ(x,y)with the cross section|q|=r,and A(x,y)∈Uthe last intersection point with the cross section|p|=r.Let Obe a small neighborhood of A(W)in U.

We introduce a symplectic relation R⊂O×Oas follows:(B,B)∈R if there is a trajectory on the energy levelΣjoining Bwith Band close to the heteroclinics inσ(W).Under certain transversality conditions(nonconjugacy of Aand Aalongσ),which one can verify as in[7],to any X=(y,p,x,q)in an open set D⊂Rthere correspond points B=(x,y,q,p)∈Osuch that(B,B)∈R.We obtain:

Proposition 3.6.The relation R is given by a generating function R(X),X =(y,p,x,q)∈D,as follows:

We denote by B(X)the points corresponding to X∈D.

Suppose now thatµ>0 is sufficiently small and letµ∈[−µ,µ].Proposition 3.6 implies

Corollary 3.2.For anyµ∈[−µ,µ]and X=(y,p,x,q)∈D there exist x,p,y,qsuch that the points B(X,µ)= (x,y,q,p)∈ Σare joined by a trajectory inΣ,smoothly depending onµ.The symplectic relation Rbetween Bis given by a generating function R(X)=R(X)+O(µ):

(B,B)∈R⇔ d R(X)=pd q+yd x+xd y+qd p.

Let Sbe the generating functions(3.3)of the local stable and unstable manifolds W(V).Set

Eqs.(3.5a),(3.5b)and(3.16)imply:

Proposition 3.7.

•The critical value is the generating function of the scattering map:

Next we introduce a discrete action functional whose critical points correspond to heteroclinic chains.

In a neighborhood U～=V×B×Bof Vin M we will use symplectic coordinates(x,y,q,p)as in(3.1).Let

be the exit point ofσfrom U,and

given by the generating function R(X)via

are joined by a trajectory onΣclose toσ.

Let

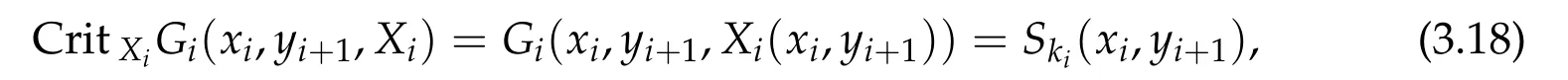
which is the generating function of the symplectic map f.

Let us define a formal discrete action functional

where

The functional is defined on V×D,where

Proposition 3.8.

•For any z∈V close to c(with small‖z−c‖),the function X∈D→B(z,X)has a strongly nondegenerate critical point X(z).

•The(formal)critical value equals the action functional(2.2):

A(z)=B(z,X(z)).

•If c is a strongly nondegenerate critical point of A,then(c,X(c))is a strongly nondegenerate critical point of B on V×D.

We call a critical point strongly nondegenerate if the Hessian has an inverse which is bounded in l.The first item of Proposition 3.8 follows from the fact that for fixed z the functional split into a sum of independent functions of X,and these functions have nondegenerate critical points with the critical values(3.18).The rest follows easily.

By Corollaries 3.1 and 3.2,

‖∇A−∇B‖≤Cµ|lnµ|.

By Proposition 3.8,the functional B has a strongly nondegenerate critical point(c,X(c)).

Now the proof is completed by the implicit function theorem in l.

4 Slowly time dependent systems

the stable and unstable manifolds of the equilibrium z(τ).Ifγ:R→W(τ)∩W(τ)is a transverse homoclinic orbit of the frozen system:

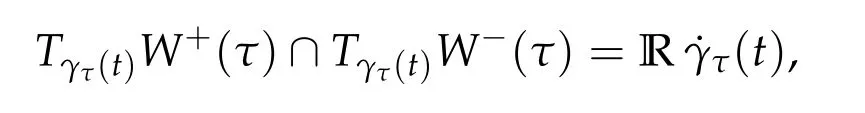
then it smoothly depends onτ.The Maupertuis action

is called the Poincar´e potential,and

is called Melnikov’s function.Ifωis nonexact,the Poincar´e potential may be multivalued,but P(τ)is always correctly defined.

Let us find the scattering map for the extended system(1.4).The stable and unstable manifolds W(τ,h)of a point(z(τ),τ,h)∈ˆN are

A homoclinicγof the frozen system defines a family of heteroclinics

of the extended system,where by(4.3),

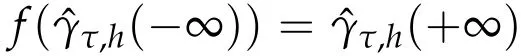
The Hamiltonian(1.5)is unbounded as h→0.Thus we fix smallδ>0 and study the system for h∈[δ,δ].Then we can try to apply the results of section 2 to the symplectic critical manifold

f(τ,h)=(τ,h+n P(τ))

S(τ,h)=τh+P(τ).

As in Section 2,we assume that the leading eigenvalues of the equilibrium z(τ)are simple.In the real case they are±α(τ),and in the complex case±α(τ)±iβ(τ).

We construct trajectories with negative energy corresponding to a negative code.For positive codes and positive energy there is a similar result.Theorem 2.3 withµ=−ε<0 implies the following:

•E(0)=−εhand E(t)<0 for 0≤t≤T=(τ−τ)/ε.

•The sequencesτand h=−E(t)/εsatisfy

Thus(τ,h)shadows a trajectory of the scattering map F.

Theorem 4.1 was proved in[4]by a different method.The complex case was not considered in[4].Then we use Theorem 2.4.The code is now a pair of sequences(k,n),where the sequence k∈K is arbitrary and 0≤n≤m.The assertion is the same except that(4.4a)is replaced by

where O(ε)is bounded independent of n.

Appendix

We have seen that for H=o(ε)the reduction(1.5)does not work.Let us discuss this case briefly.The frozen system has a compact normally hyperbolic invariant manifold N={(z(τ),τ):τ∈T}in M×T.Hence for smallεthere is a normally hyperbolic compact invariant manifold

N={(z(τ),τ):τ∈T}, z(τ)=z(τ)+O(ε).

By(1.3)we have H|=H(z(τ),τ)=O(ε).Let us describe multibump trajectories coming exponentially close to N.

0<δ

Atrajectory will correspond to a code which is a strictly increasing sequence(τ∈T).

Theorem A.1.Suppose thatε>0 is sufficiently small.Then for any code(τ)there exists a unique trajectoryγ(t)∈M,τ=τ+εt,such that for all i∈Z,

•d((γ(t),τ),N)≤efor min|τ−τ|≥δ.

Acknowledgements

This work is supported by the Russian Science Foundation under grant No.19-71-30012.