一种分步式建筑物屋顶面点云高精度提取方法
周钦坤 岳建平 李乐乐 杨 恒
1 河海大学地球科学与工程学院,南京市佛城西路8号,211100 2 苏州工业园区测绘地理信息有限公司,江苏省苏州市苏虹中路101号,215000
主流的基于机载激光雷达数据的建筑物三维模型重建方法包括基于模型驱动的三维重建与基于数据驱动的三维重建,其中建筑物屋顶面的提取是数据驱动方式中最为关键的一个步骤,提取质量的好坏直接关系到后续建筑物拓扑重建的成败[1]。由于受机载激光雷达点云分布不连续、不规则及建筑物多层次、多面片的复杂结构等因素的影响,从机载激光雷达点云数据中提取高精度建筑物屋顶面仍面临着较大的挑战。
学者们围绕屋顶面的高精度提取开展了众多研究,提出了数据聚类[2-3]、区域增长[4-5]、模型拟合[6-9]、能量函数最小化[10]等方法。本文针对现有方法存在建筑物屋顶面提取精度较低、适应性较差等问题,提出了一种分步式建筑物屋顶面点云高精度提取方法。
1 分步式提取方法
首先通过预处理选取可靠平面点,利用K-means算法实现可靠点在法向量空间上的聚类;再通过逐步平面估计,提取初始屋顶面片;在此基础上,进行面片的合并与未标记点的归属判断。
1.1 预处理
点云法向量是建筑物屋顶面提取的重要依据,其在屋脊线等屋顶面交互处通常难以被准确计算[11-12],在法向量空间域中表现为错乱分布的点,不利于后续的聚类操作。为保证面片提取的准确性,首先对屋顶点云进行预处理,以得到法向量下可靠的平面点,主要包括以下步骤:

(1)
(2)
2)可靠平面点的选取。每个点均被赋予一个可靠性指标,理论上该值越小,该点越可靠,可选取可靠性指标较好的点组成可靠平面点集seed:
seed={p|ασ<αn,n=L/k,
k=max(Kg,Kw)}
(3)
式中,αn为可靠性指标降序排列时第n个点对应的ασ值,L为建筑物屋顶面点云总个数,Kw为屋顶面片聚类数,数值上等于后续K-means算法中的参数K,参数K随后续的迭代计算而动态确定。Kg为固定值,可根据屋顶面实际情况在5~7中取值,以防止因去除过多的点而使屋顶面提取困难。
图1(a)~1(c)分别为建筑物屋顶面影像、屋顶点云可靠性分布及可靠平面点选取结果,图1(c)中黑色点云为选取的可靠平面点,经过预处理将法向量分布离散的点云去除,对应图1(d)中红色点云。典型建筑物屋顶由多个平面构成,每个平面点云的法向量会指向特定方向。图1(d)为屋顶点云的法向量空间分布,即屋顶点云法向量在高斯球上的分布情况,红色为根据可靠性指标去除的点云,其他不同颜色代表不同屋顶面的可靠平面点,可见同一屋顶面上可靠平面点在法向量空间上是较为集中的,不同屋顶面上则相互分离,因此可通过点云法向量空间分布提取建筑物屋顶面片。

图1 可靠性指标分布及可靠平面点选取Fig.1 Distribution of reliability index and selection of reliable plane points
1.2 屋顶面片初步提取
K-means算法是无监督的聚类算法,对于屋顶点云法向量这样的类球形分布,其聚类效果较好,且实现简单,调试的参数仅为聚类个数K。本文通过设置聚类指标实现参数K的动态确定,基本原理如下:K-means算法要求簇内各点尽量紧密连接在一起,而簇间距离尽可能大,当K值恰好等于实际所需的聚类数时,屋顶点云在法向量空间上正确聚类;随着K值的继续增大,某一屋顶面点云将会被分成数簇,即会存在法向量指向相近的数个簇,此后最大的簇间单位法向量点积会趋近于1且保持稳定。所以可取最大簇间单位法向量点积作为聚类指标,K值即为使聚类指标趋近于1且保持稳定的前一个聚类个数,如图2中红色标记点横坐标为对应的聚类个数。

图2 K-means算法聚类指标与聚类个数折线图Fig.2 K-means clustering index and clustering number
通过聚类操作,将法向量指向近似的点云归为同类,但若建筑物存在平行或近似平行的屋顶,即法向量指向相近但空间上相离的屋顶,则需对其进行进一步区分。本文采用逐步平面估计法进行此类屋顶面的提取,具体步骤如下:
1)取某一聚类全部点云单位法向量加权得到的聚类法向量n,并选此聚类中ασ最小的点pmin(ασ)(可认为此点是平面性最可靠的点),pmin(ασ)∈R3,构建平面方程P1:
n·(x,y,z)T-n·(pmin(ασ))T=0
(4)
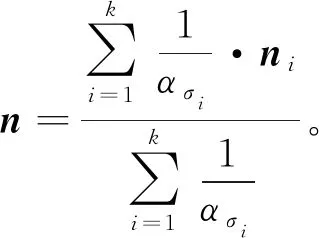
2)计算聚类中各点到平面P1的距离,若小于给定阈值,则判断此点为平面上一点,进行联通性分析,取最大联通子集为当前平面的内点;
3)对内点进行最小二乘拟合,确定平面P2;
4)计算聚类中各点到平面P2的距离,重复步骤2)的操作,记第i次估计平面P2时P2内点个数为num2i;
5)若相邻2次平面P2检测的内点数量趋近恒定,即|num2i-num2i-1|<ɛ,则跳转至步骤6),否则重复步骤3)和4);
6)从聚类中移除内点,并重复步骤1)~5)进行迭代,由于屋顶平行面片个数一般有限,迭代次数一般不大于10。
本文提出的逐步平面估计是一个寻找最佳屋顶平面的过程,由于法向量的计算误差与聚类中近似平行面片的存在,从整个聚类中得到的某一屋顶平面较为粗糙。通过步骤1)法向量加权与最可靠点的选取,使得P1大体逼近屋顶面片,P1的内点即为某一屋顶面上的点云,由此部分点可拟合出更优的屋顶平面P2,得到更多的屋顶面内点,通过数次内点拟合即可逐步修正平面P2,使其成为最佳平面。上述操作进行了2次连通性分析,第1次是为了剔除由于平面P1的误差纳入的其他屋顶点,进而依据剩余内点拟合得到更优平面;第2次是为了去除在数学意义上共面而在空间上分离的点,得到纯净的单一屋顶面片。逐步平面估计屋顶面的提取结果见图3(c),可以看出,该算法能较好地分离平行屋顶面。与RANSAC算法相比,该方法不用设置最小面片点数且不用随机选点以构成平面模型,避免了由于选点不在同一平面而造成的大量不必要的计算。

图3 聚类结果及逐步平面估计结果Fig.3 The results of clustering and stepwise plane estimation
1.3 面片后处理
面片后处理主要包括面片合并及未标记点的归类。由于法向量计算不准确及K-means聚类误差等因素,部分屋顶面经过粗提取后可能形成多个面片,如图4(a)所示。由于屋顶面A、B近似平行且存在上述误差,使得屋顶面B中的一部分与屋顶面A聚为一类,在逐步平面估计后,屋顶面B将会形成2个破碎面片,如图4(b)所示。为得到完整的屋顶面,需合并属于同一屋顶面的多个面片。令已找到的屋顶面片为M={m1,m2,…,mn},寻找面片mi的相邻面片,首先定义面片邻域Ner,即由面片中每个点的邻域点面片号构成的无重复标号集合,搜索面片mi的Ner,其中每个标号都代表面片mi的一个相邻面片,计算面片mi与各个相邻面片的最小二乘拟合平面残差平方和,若残差平方和小于阈值,则将面片mi与相应相邻面片合并。重复上述过程2~3次,即可实现屋顶面片的完整提取,面片合并结果见图4(c)。

图4 屋顶面片合并Fig.4 Merging of roof patch

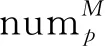

图5 未标记点归类Fig.5 Classification of unmarked points
2 实验与分析
2.1 实验数据与方法
为验证本文算法的可行性与稳定性,选取Vaihingen机载LiDAR数据集中部分建筑物的点云数据进行实验。由于本文研究主体为建筑物屋顶,因此地面点、植被点及建筑物立面点等数据均已被剔除。

2.2 实验结果及定性分析
各算法的提取结果如图6所示,图中不同颜色代表提取的不同屋顶面,其中红色点为未能提取出的屋顶面或屋顶附属物点。通过与航空影像进行对比可以看出,RANSAC算法及区域增长算法的提取效果与本文算法相比差异较大。

图6 单个建筑物屋顶面提取结果Fig.6 Extraction results of roof surface for single building
区域增长算法仅依靠种子点与待判断点之间的法向量夹角及粗糙度等局部特征进行生长,所以分割结果与局部特征的计算精度息息相关。由于局部特征计算的不稳定性,导致建筑物屋顶将存在不同程度的边界模糊问题,如建筑物4(矩形框区域,下同)。同时,对于较小的屋顶面如建筑物3,计算出的法向量指向杂乱,无法实现有效的聚类,而在过渡平缓的相邻屋顶面处,由于局部特征变化较小,会形成屋顶面的欠分割,如建筑物1和2。此外,在邻接关系复杂的区域容易形成过分割,如建筑物6。
RANSAC算法的每次随机采样估计模型会获取点数最多的屋顶面,两屋顶面相交处的点被优先划分到较大的屋顶面,形成屋顶竞争现象,造成边界不明确,如建筑物5。由于RANSAC算法需要设置最小面片点数阈值,而全局最优的阈值难以找到,当采用较大的阈值时,较小的屋顶面由于达不到阈值条件而无法提取,如建筑物3和10;当阈值设置较小时,较大的屋顶面可能会因为过早地满足阈值条件而变得破碎,如建筑物9。此外,受限于算法本身的原理,对于曲率变化较大的屋顶区域,如建筑物7,无法实现有效提取。
相较于以上2种算法,本文算法的提取结果更加优异,拓扑关系更加清晰,且不会受屋顶面大小差异、数量多少及复杂程度等的影响,具有更高的稳定性。但本文算法本质上是一种平面提取算法,对于如建筑物7的屋顶面,与RANSAC算法一样,提取效果较差。此外,本文算法依赖于可靠平面点,若屋顶面过小且点密度太低,导致计算出的法向量不准确,则屋顶面将不存在可靠平面点,该屋顶面的提取也会失败,如建筑物8。
2.3 定量分析与评价
建筑物屋顶面在空间上为平面,在机载LiDAR点云数据中表现为点集,故本文从点与面2个维度对提取结果进行定量分析,在面维度上借鉴文献[13]中的质量评价标准,在点维度上参考文献[3]与[14]的评价方法。
由表1(单位%)可知,RANSAC算法与区域增长算法在提取完整率上与本文算法精度相仿,其原因为对两者增加了连通性分析与未归类点的二次判断等措施;但在正确率与提取质量上,RANSAC算法及区域增长算法与本文算法依然存在较大差距,尤其是区域增长算法,说明这2种算法存在较为严重的过分割与欠分割等问题。结合表2可以发现,本文算法能正确提取绝大多数屋顶面,而RANSAC算法与区域增长算法的提取效果较差。观察建筑物影像可知,本文算法未能正确提取的主要为面积较小(包含的脚点数较少)的屋顶面或曲率变化较大的非平面屋顶面。此外,RANSAC算法与区域增长算法对过渡平缓及拓扑关系复杂的屋顶面也存在错误提取的情况。表1和2中维度的精度统计结果共同验证了§2.2中的定性分析结论,并进一步证明本文算法对不同复杂程度的建筑物屋顶面的提取具有适应性与准确性。

表1 屋顶面点维度提取精度统计

表2 屋顶面面维度提取精度统计
为比较不同算法的提取效率,统计各算法对不同屋顶面的提取时间,结果如图7所示。由图可知,本文算法的提取效率与区域增长算法相近,明显优于RANSAC算法。虽然本质上同为平面提取算法,但本文算法首先将近似平行屋顶聚类,然后通过逐步平面估计等措施提取屋顶面,避免了RANSAC算法因对建筑物屋顶面整体选点构建平面模型而造成的大量不必要计算,故提取时间较RANSAC算法明显缩短。
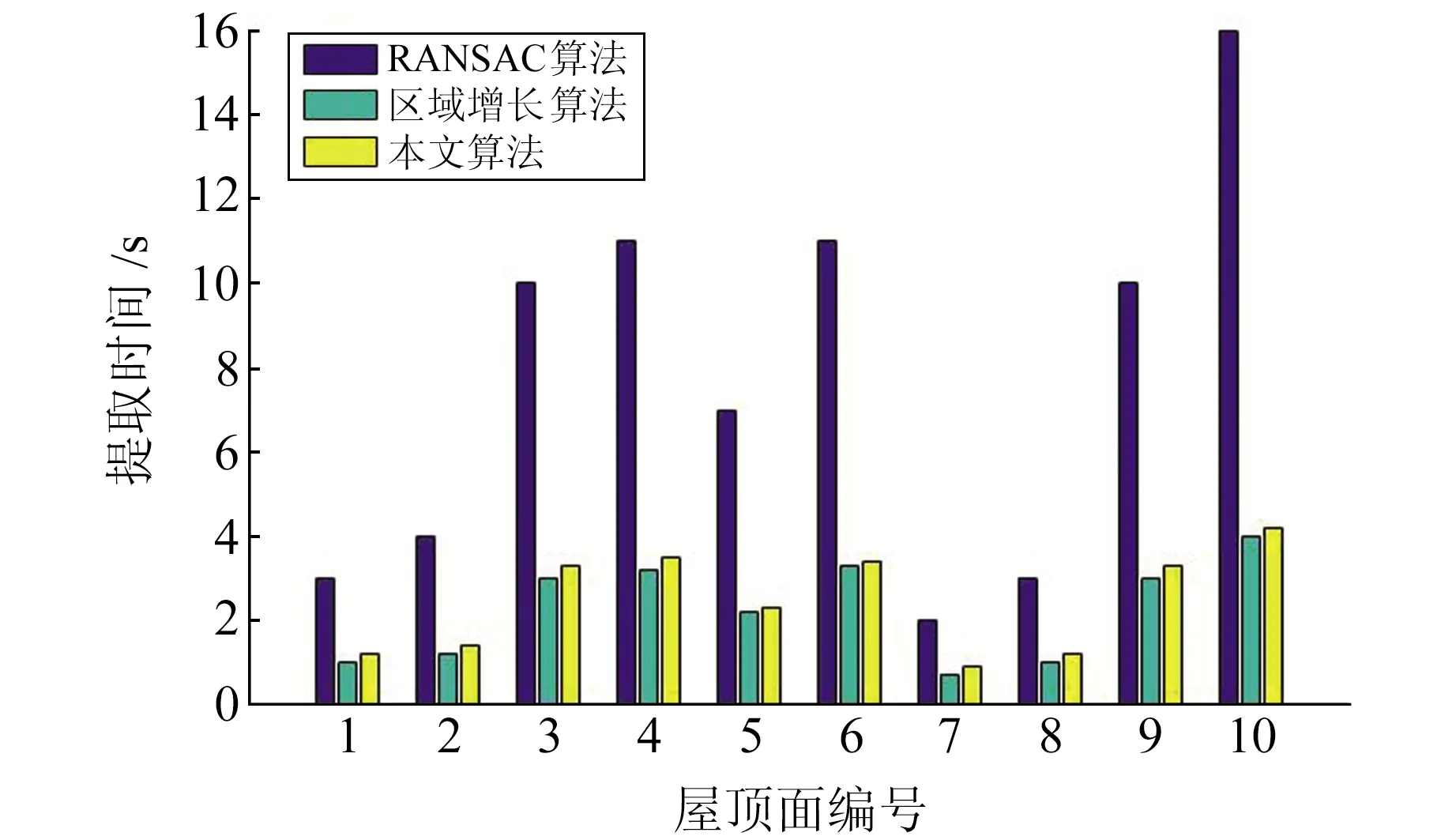
图7 各算法提取时间统计Fig.7 Statistics for extraction time of each algorithm
通过定性分析与定量评价可知,本文算法明显优于其他2种算法,对于屋顶结构复杂的各类建筑物也有较好的提取效果,其主要原因为:1)将可靠平面点与非可靠平面点分别进行处理,在将可靠平面点聚类得到平行屋顶面时,可避免非可靠点对聚类的影响;2)采用由粗到精的分步式处理方式,即先将平行屋顶聚类,然后通过逐步平面估计等措施提取初始屋顶面,再进行细化处理得到建筑物完整屋顶面;3)面片合并较好地解决了屋顶面的过分割,保证了屋顶面的完整性,对未标记点进行归属判断,避免了屋顶面的竞争现象,可得到更加清晰的面片边界。
3 结 语
本文针对复杂建筑物屋顶面提取存在的问题,提出一种分步式建筑物屋顶面点云高精度提取方法。实验结果表明,相较于传统方法,本文方法的提取结果更优,且提取效率较高,对不同复杂程度的建筑物屋顶面均能取得较好的提取效果,具有较强的适应性与准确性。由于本文算法本质上也是平面提取算法,故无法有效提取曲面屋顶,另外本文算法依赖于可靠平面点的选取,不能有效提取不存在可靠平面点的小屋顶面。如何准确估计点云法向量以得到小屋顶面的可靠平面点,将是后续研究的重点。

