长三角地区GNSS可降水量直接转换模型研究

范 頔 李 黎 刘 彦 韦 晔韦 云 周嘉陵 刘 宇

1 苏州科技大学地理科学与测绘工程学院，江苏省苏州市学府路99号，215009 2 苏州科技大学北斗导航与环境感知研究中心，江苏省苏州市学府路99号，215009 3 江苏省气象科学研究所,南京市昆仑路16号,210009

大气可降水量(precipitable water vapor, PWV)是表征大气中水汽含量的主要参数之一，在强降雨发生前后PWV值会出现快速聚集和释放的现象，对实际降水预报有很好的指示意义，PWV序列资料可应用于暴雨短期临近预报研究[1]。近年随着CORS站数量的快速增加，GNSS-PWV逐步被运用于大气遥感和气象预报中[2-3]。

国内外许多学者已经对获取GNSS-PWV及其气象应用进行了大量研究[4-8]。本文采用2017年长三角地区7个CORS站的GNSS和气象数据，利用线性回归及最小二乘拟合法建立GNSS-PWV与GNSS-ZTD、地面气温(T)、地面气压(P)之间的函数模型，并将利用该模型计算得到的PWV值与GNSS-PWV(作为真值)进行比较，以验证模型的精度，同时利用2018年长三角地区4个CORS站的GNSS-PWV数据对该PWV模型的预报精度进行评估。

1 数据来源及其相关性分析

1.1 数据来源

本文选取长三角地区7个测站2017年采样率为1 h的GNSS数据及2018年采样率为3 h的气象数据作为实验数据，主要包括PWV、ZTD、地面气温、相对湿度和气压等，表1为GNSS测站的空间位置。可以看出，用于研究的7个GNSS气象观测站位于26°～34°N、116°～122°E区域内，均匀覆盖了长三角大部分区域。

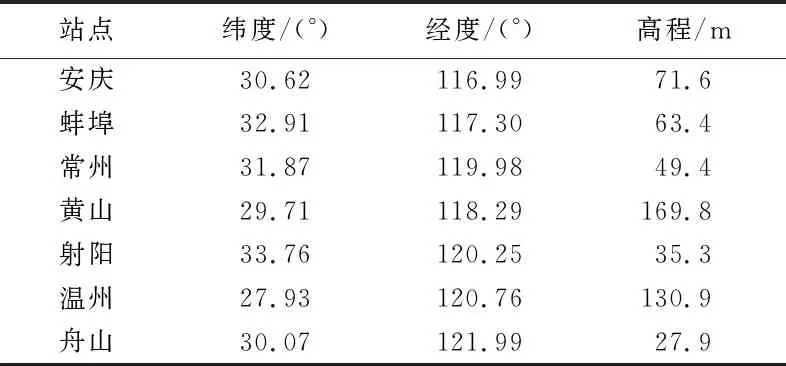
表1 选用的GNSS测站空间位置

1.2 影响因子相关性验证

在GNSS气象学中，PWV与ZTD、P、T之间存在一定的相关性，图1为其相关性分析，R为相关系数。由图可知，PWV与ZTD、T之间具有良好的正相关性，与P之间具有一定的负相关性。各因子中与ZTD的相关系数最大，达到0.99，说明ZTD对PWV的影响最大，气压P与气温T对PWV也有较大影响。

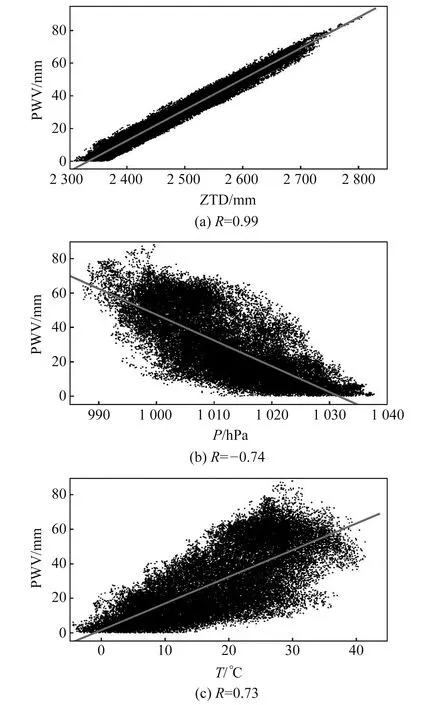
图1 PWV与ZTD、P、T之间的相关性分析Fig.1 Correlation analysis between PWV and ZTD, P,T

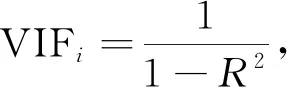
表2 不同参数间相关性分析统计

2 区域PWV直接转换模型的建立及精度分析

2.1 全年PWV模型

2.1.1 PWV建模方法

1) 多因子PWV模型。基于GNSS-PWV(作为真值)和ZTD、T、P之间的线性相关，利用多元线性拟合法，假设线性方程为：

PWV=a0+a1ZTD+a2T+a3P

(1)

将7个测站的PWV、ZTD、T、P代入式(1)，利用最小二乘原理计算出系数a0、a1、a2、a3，得到的多因子方程为：

PWV=-24.984 6+0.161 9ZTD+

0.096 2T-0.346 1P

(2)

式中，PWV和ZTD的单位为mm，气压P的单位为hPa，气温T的单位为℃。

2) 双因子(ZTD和T)PWV模型。对7个测站2017年的PWV和ZTD、T进行二元线性拟合，得到双因子PWV模型为：

PWV=-421.021 3+0.179 9ZTD+

0.180 4T

(3)

3)双因子(ZTD和P)PWV模型。对7个测站2017年的PWV和ZTD、P进行二元线性拟合，得到双因子PWV模型为：

PWV=-7.942 6+0.164 9ZTD-

0.368 8P

(4)

4) 单因子PWV模型。对7个测站2017年的PWV和ZTD进行一元线性拟合，得到单因子PWV模型为：

PWV=-444.110 0+0.189 8ZTD

(5)

2.1.2 精度检验

为验证PWV模型的精度，将计算的2017～2018年PWV模型值与GNSS-PWV(作为真值)进行对比，图2为安庆、常州、射阳、温州4个测站的PWV模型值与真值的偏差。可以看出，安庆、常州和射阳等3个测站的单因子模型和2种双因子模型的PWV模型值在夏、秋季节比真值大，在冬、春季节比真值小；温州站的单因子和双因子模型的PWV值绝大部分大于真值；多因子模型的PWV值均匀分布在真值两侧。尽管温州站的单因子和双因子模型均表现出显著负偏差，但多因子模型修正了这种偏差。从模型偏差来看，全年单因子PWV模型的偏差基本都在10 mm以内；不含P的双因子PWV模型的偏差大部分在7 mm以内；不含T的双因子PWV模型的偏差在5 mm以内；多因子PWV模型的偏差大部分在1 mm以内，精度最高。

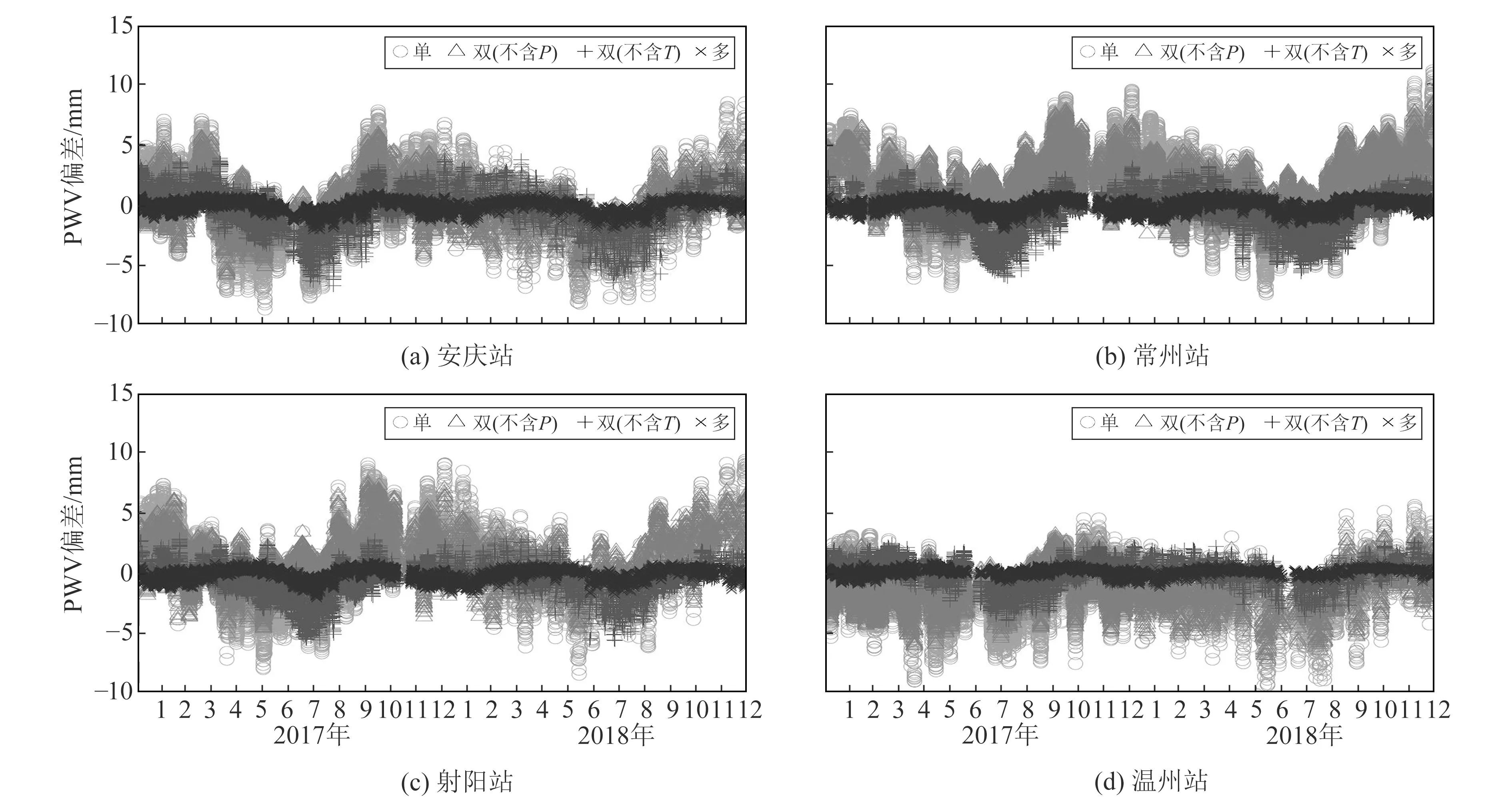
图2 2017～2018年4个测站的PWV偏差Fig.2 PWV deviation at 4 stations during 2017-2018

表3(单位mm)为PWV直接转换模型的精度统计，从表中可知，仅含有ZTD的单因子模型的RMS为3.07 mm，精度较低，加入P的双因子模型RMS降到2.35 mm，加入T的双因子模型RMS降低到1.18 mm，精度有一定的提高；含有ZTD、T、P的多因子模型RMS降到0.47 mm，精度有大幅度提高。由此可见，长三角地区选用多因子PWV直接转换模型最为合适。

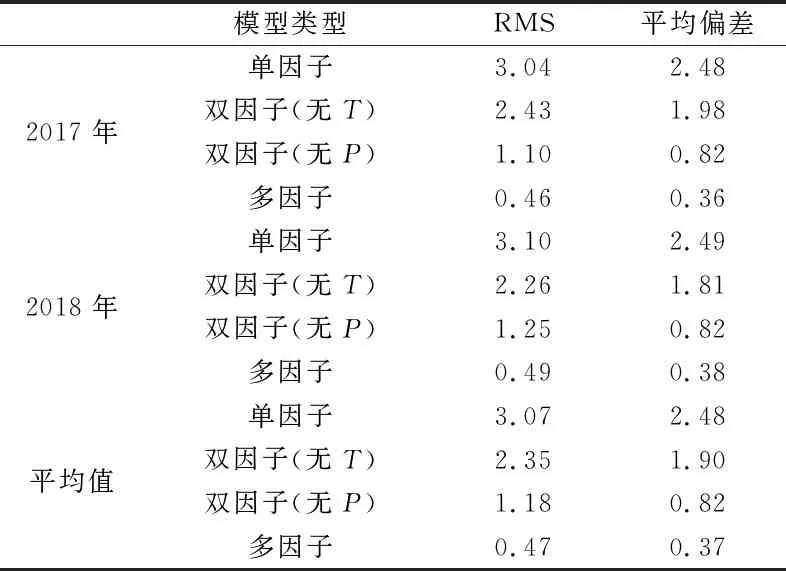
表3 PWV模型全年精度统计

2.2 分季节多因子PWV模型的建立及精度分析

分析可知，PWV值呈周期性变化，夏秋季节较高、冬春季节较低，因此PWV值与季节存在一定的相关性。由于多因子模型具有最佳的预报精度，本文将进一步建立分季节多因子PWV模型，具体见表4。

表4 分季节多因子PWV模型

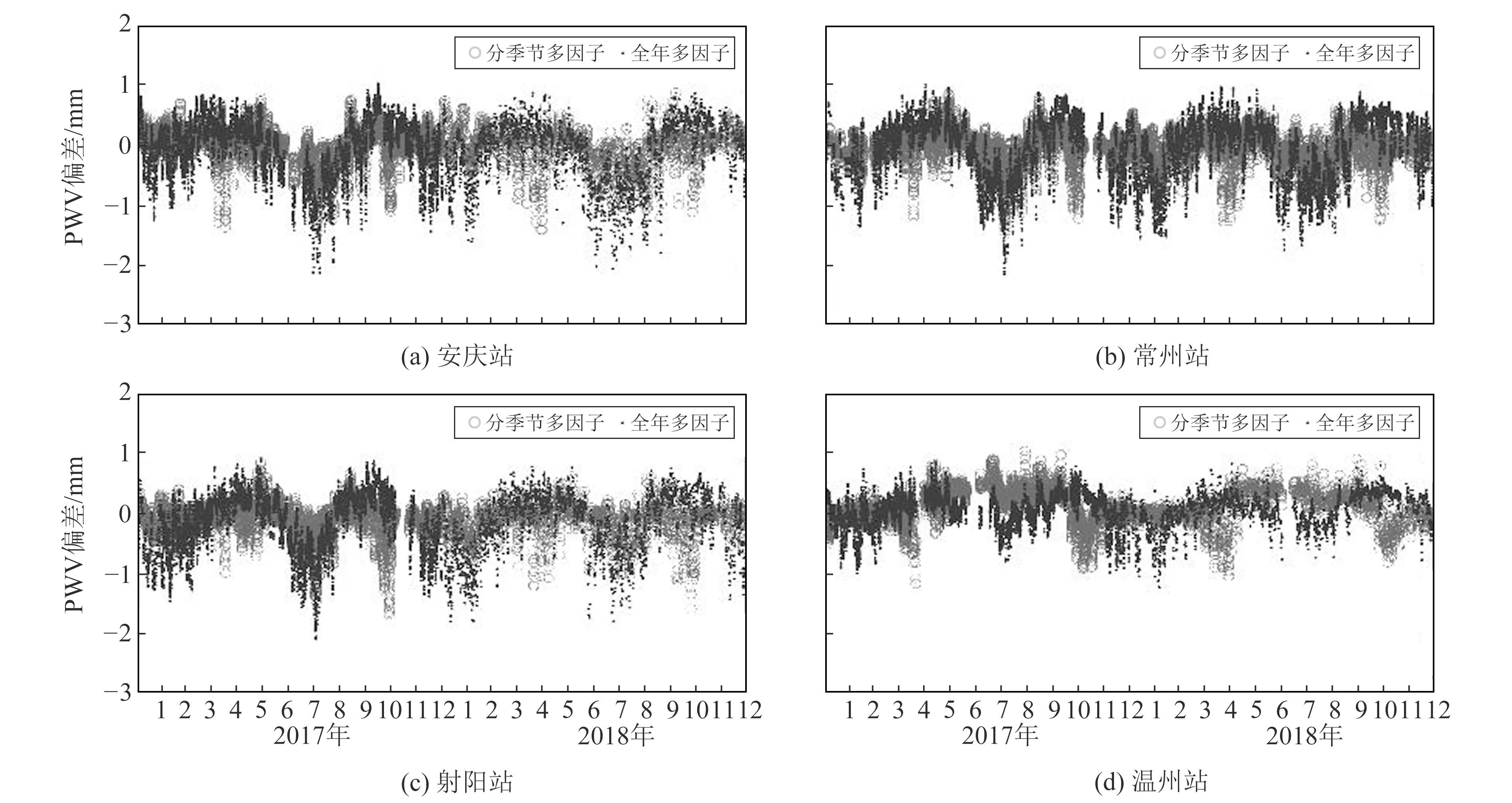
图3 2017～2018年安庆站、常州站、射阳站、温州站PWV模型值偏差Fig.3 Deviations of modelling PWV value at Anqing, Changzhou, Sheyang, and Wenzhou stations during 2017-2018

图3为安庆、常州、射阳、温州等4个GNSS测站利用分季节多因子模型及全年多因子模型得到的PWV模型值与GNSS-PWV真值之间的对比，可以看出，安庆站夏季和冬季的分季节多因子模型的精度比全年模型高；常州站分季节多因子模型偏差比全年模型小；射阳站在夏、冬两季采用分季节多因子模型可以降低模型偏差，而春、秋两季使用全年多因子模型具有更好的精度；温州站两种模型的偏差都非常小。

表5 (单位mm)为2017～2018年分季节多因子模型的精度统计，可以看出，分季节多因子模型较全年多因子模型具有更高的精度：春季的RMS从0.41 mm降低到0.24 mm，夏季的RMS从0.47 mm降低到0.32 mm，秋季的RMS从0.50 mm降低到0.37 mm，冬季的RMS从0.48 mm大幅降低到0.19 mm。虽然采用分季节多因子模型能够降低PWV模型值与真值之间的偏差，但分季节多因子模型与全年多因子模型的精度均在1 mm以内，均能满足GNSS-PWV业务应用的精度需要。

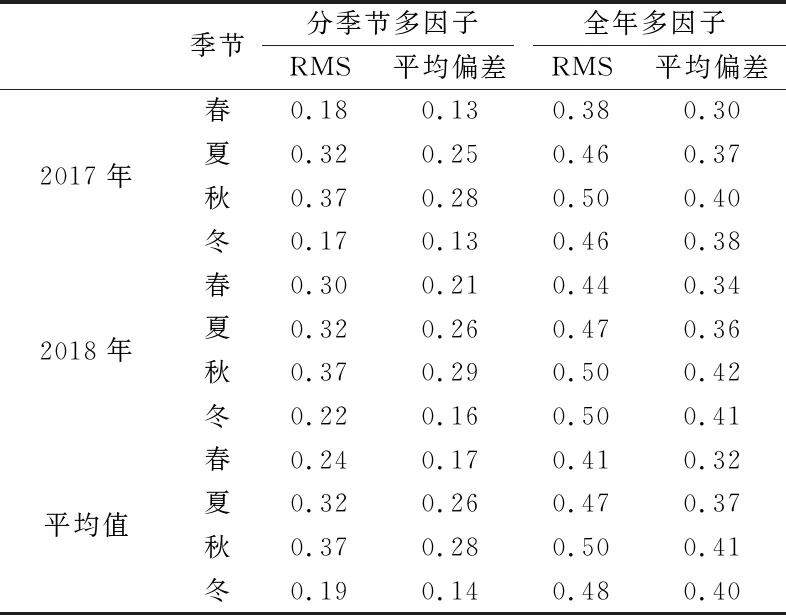
表5 分季节PWV区域模型精度统计

3 结 语

本文利用长三角地区2017～2018年7个测站的GNSS和气象数据，通过对PWV、ZTD、地面气温T、地面气压P等参数进行相关性分析，构建了长三角地区的PWV直接转换预报模型，得出以下结论：

1)PWV与ZTD之间具有良好的相关性，相关系数为0.99； PWV与P、T之间具有较好的相关性，相关系数分别为-0.74和0.73。

2)基于ZTD的单因子PWV模型平均偏差为2.48 mm、RMS为3.07 mm；基于ZTD和P的双因子PWV模型平均偏差为1.90 mm、RMS为 2.35 mm，基于ZTD和T的双因子PWV模型平均偏差为0.82 mm、RMS为1.18 mm；基于ZTD、T和P的多因子PWV模型平均偏差为0.37 mm、RMS为0.47 mm。

3)基于ZTD、T和P的分季节多因子PWV模型的平均RMS为0.28 mm，比全年多因子PWV模型的精度略有提高，长三角地区采用这两类多因子PWV模型均能获得预测精度优于1 mm的PWV预报值。