一种应用改进符号序列熵与滑动窗奇异值的退化特征提取方法

王微　王冰　胡雄　孙德建　张道兵

摘要： 为了准确跟踪岸桥关键部件的性能退化状态，提出一种基于改进符号序列熵与滑动窗奇异值的在线退化特征提取方法。针对岸桥工况特殊、振动随机冲击频繁的特点，引入阈值因子并改进序列符号化方法，在保留方向变化信息的同时兼顾“粗粒化”的幅值变化信息，从而提高符号序列熵滤除随机冲击、刻画振动信号复杂度大小的能力。在线计算振动信号的改进符号序列熵，结合滑动窗方法，循环提取改进符号序列熵序列的奇异值，以此作为岸桥关键部件的在线退化特征。分别采用来自上海港集装箱码头的起升减速箱与轨道铰点的全寿命振动信号进行实例分析，结果表明：滑动窗奇异值能够刻画起升减速箱和轨道铰点的性能退化程度，退化程度越深，取值越大;并且具有计算稳定、快速的优点，能够为准确跟踪并评估健康状态奠定方法基础。

关键词： 信号处理; 岸桥; 退化特征提取; 符号序列熵; 奇异值分解

中图分类号： TN911.7; TH132.4    文献标志码： A    文章编号： 1004-4523（2021）01-0211-08

DOI：10.16385/j.cnki.issn.1004-4523.2021.01.024

1 概 述

岸橋又称为岸边集装箱起重机、桥吊，是用来在岸边对集装箱进行装卸的大型港口起重设备。起升机构和轨道铰点是岸桥设备中重要的机构和结构部件。其中起升机构是集装箱升降运动的动力机构，一般由驱动电机、齿轮箱、卷筒以及钢丝绳等设备组成。轨道铰点是前、后大梁的结构链接器，是岸桥大梁结构稳固的重要保证。实景图如图1所示。岸桥运行环境恶劣且工况特殊，在高速、重载、大冲击的周期性吊装作业中，小车频繁通过轨道铰点引起强烈振动，集装箱瞬间启停引发的强烈动载也会对起升齿轮箱造成振动冲击。长期作用下会诱发这些关键部件的性能退化甚至突发故障^[1]，导致停工停产甚至是人员伤亡。目前，起升齿轮箱和轨道铰点已成为岸桥设备管理中的易损部件和健康薄弱环节。如果能够在线监测其振动信号，从中挖掘得到退化特征指标，就可以准确跟踪其性能退化趋势，为开展岸桥的视情维修，提高安全可靠性奠定方法基础。

特征提取是视情维修（Condition?Based Maintenance，CBM）中的关键步骤^[2]，是实现健康状态评估的基础。特征提取的目标是在监测信号中挖掘能够反映性能退化趋势的定量指标。目前应用较多的方法以时域、频域以及时频域等线性分析方法为主^[3?5]，提出了基于RMS谱^[6]、峭度^[7]、谱峭度^[8]等性能退化指标。考虑到机械振动信号的非线性、非平稳特性，近年来，基于信息熵与分形的复杂性分析方法开始应用到轴承、齿轮等旋转机械的退化规律分析中，文献[9]提出了S时频熵指标用来度量轴承振动信号的复杂度并反映其退化过程;文献[10] 提取轴承振动信号的多尺度模糊熵和VMD能谱熵作为退化特征向量，利用全寿命数据样本的退化特征向量训练不同退化状态下的HMM模型，最后通过建立的HMM模型库并根据最大对数似然概率原则识别轴承退化状态。除此之外，还包括多元多尺度熵^[11]、多尺度置换熵^[12]等退化特征。

前期研究表明，岸桥振动监测信号具有一定程度的复杂特性。但由于运行环境和工况特点，振动信号中包括了大量的随机冲击成分，直接影响了信息熵和分形维数的精确化计算，使得结果波动性强，无法准确反映信号内部的复杂规律。作为一种“粗粒化”的信号分析方法^[13]，符号动力学分析能够采用符号化方法处理时间序列，保留幅值变化的方向性信息。以此为基础的符号序列熵方法已经成功地应用在脑电信号分析中^[14?16]，具有计算简便、运算速度快、抗干扰能力强的优点。目前该算法较少应用在机械设备特征分析领域，考虑到岸桥振动信号非平稳、冲击大的特点以及该方法在幅值处理“粗粒化”的特性，采用符号序列熵挖掘岸桥设备性能退化特征具有一定的可行性。

针对岸桥工况特殊、振动随机冲击频繁的特点，本文以符号序列熵、奇异值分解为基础，提出一种基于改进符号序列熵与滑动窗奇异值的在线退化特征提取方法。引入阈值因子对符号序列熵进行改进，提出在线退化特征提取流程。以起升减速箱和轨道铰点的全寿命振动监测信号进行方法的有效性验证。

2 符号序列熵及其改进

4 实例分析

4.1 起升减速箱与轨道铰点全寿命数据集

采用岸桥起升齿轮箱和轨道铰点的全寿命振动监测信号进行实例分析。监测对象为上海港集装箱码头某岸桥。自该岸桥列装以来，课题组NetCMAS系统一直对该设备40多个关键测点的振动、温度、应力信号进行在线监测^[19]，该系统在功能、性能、安全管理等方面都满足欧盟工业控制系统纲要规范，达到ICS Compendium工业4.0四级标准，是中国制造2025工业控制系统自动化的一个典型应用实例。岸桥的不同测点安装有振动、温度传感器以及应变片，通过电缆连接至岸桥工控机，实现状态监测数据的采集与存储。其中，起升减速箱和轨道铰点的振动信号监测如图4所示。其中，减速箱为西门子SIMOGEAR卧式斜齿轮，最大输出功率30 kW。

课题组安装的NetCMAS系统在线采样频率为24 kHz，采样时间1 s，采样间隔10 s，系统计算并存储采样时段的有效值RMS，在线获取振动RMS序列。经过约两年3个月，岸桥铰点监测位置报警，经停机检修，故障模式为垫板严重磨损，原厚度为1 mm，磨损后厚度为0.24 mm，如图5（a）所示;约经过7年8个月，起升齿轮箱高速输入轴监测位置报警，经停机检修，失效位置为输入轴调心滚子轴承，失效形式为滚子磨损，如图5（b）所示。

系统自动滤出了海量数据中的停机等非工作态数据，形成全寿命起升减速箱RMS序列Dataset1和轨道铰点RMS序列Dataset2， 图6显示了两个数据集的时域波形图。波形幅值从整体上呈现不断增大的趋势，并且包括了繁多的冲击成分。相对而言，轨道铰点处的冲击成分更大，这是由于小车频繁经过轨道铰点引发的冲击造成的。设备检修之后，波形的幅值快速下降。可以看出，RMS有效值序列的冲击成分频繁且过大，难以精确跟踪性能退化状态，甚至造成误判，有必要进行准确的退化特征挖掘。

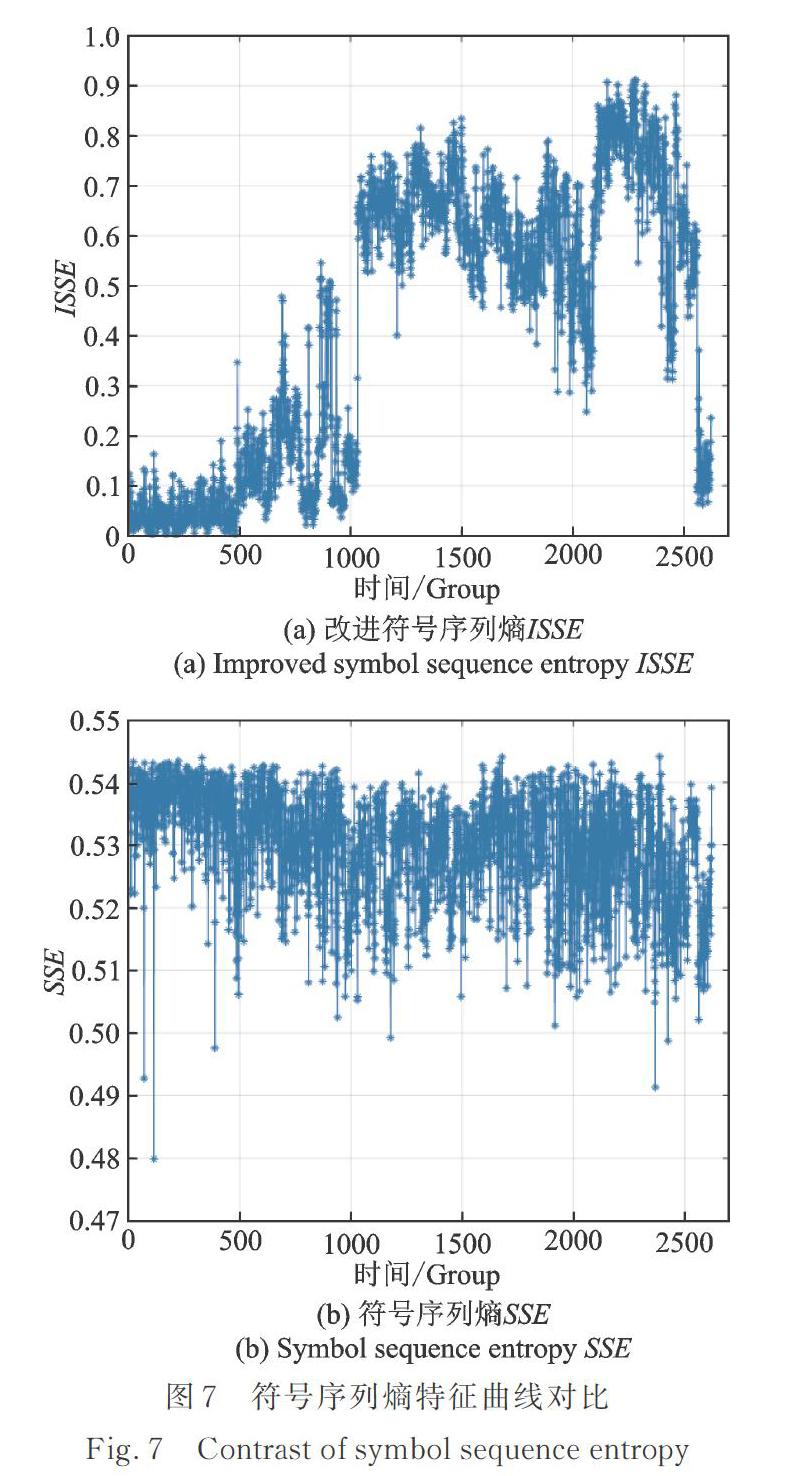
经过计算，起升减速箱全寿命演化进程中的ISSE特征序列I_j如图7（a）所示。退化程度越深，ISSE取值越大，并且具有明显的阶段性。由于RMS序列中较强的随机冲击，使得ISSE特征曲线中仍存在明显的随机波动，影响了对于性能退化趋势的精确跟踪。图7（b）对比了改进之前的SSE特征序列，该曲线随机波动性强，并且没有体现出与退化进程一致的变化趋势。主要原因在于原有的符号化方式对于随机冲击过于“敏感”，使得性能退化的主要规律“湮没”在RMS序列的随机冲击中。

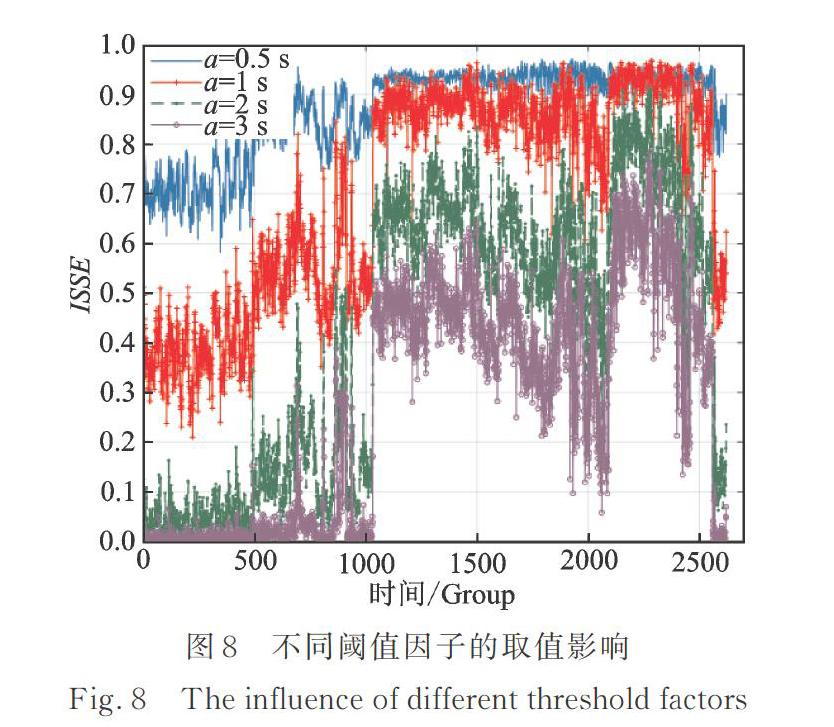
图8对比分析了采用不同阈值因子时的ISSE演化曲线。可以看出，四组曲线的整体趋势未变，但ISSE特征的值域以及阶段敏感性发生了变化。a取值越小，ISSE的值域越小，初期退化敏感性越高，后期退化曲线越平缓，敏感性越低;a取值越大，ISSE的值域越大，初期退化敏感性越低，后期退化趋势性明显，敏感性更强。主要原因在于阈值因子决定了符号化划分标准。当a值越小时，对弱冲击引起的模式变化越敏感，对强冲击的模式区分度越低。而齿轮箱性能退化的进程伴随着弱冲击成分越来越少，强冲击成分越来越多。因此，阈值因子a的取值决定了不同时期的性能退化敏感能力。为了兼顾性能整个退化过程的敏感性，本文选取阈值因子为a=2s。

图9对比分析了符号序列熵计算中m取值的影响。从图9（a）可以看出，m的取值并未影响全寿命过程中ISSE曲线的整体趋势。m取值越大，符号序列的模式种类越多，ISSE取值越大。以ISSE曲线中出现最大值的第G₂₁₅₀为例，图9（b）显示了不同m取值下该组的ISSE取值。当m值大于14时，ISSE取值几乎稳定在1。因此，为了提高ISSE对于失效的灵敏度，本文在计算中采用m=8。综上，m的取值对特征分析的影响较小，一般取3?8之间的整数，满足N>5^m即可。

为了提高退化特征的稳定性，降低随机冲击对于特征准确性的影响，采用滑动窗口?奇异值分解的方法提取奇异值，以此作为在线退化特征CV。本文设置滑动窗口宽度w=60，步长s=1。对每组滑动窗口内的ISSE序列进行奇异值分解，得到的奇异值演化曲线如图10所示。可以看出，奇异值演化曲线准确地反映了起升减速箱的退化进程，且呈现明显的阶段性。第427个滑动窗之前，奇异值SV基本上稳定在0.3附近，此时认为起升减速箱处于健康状态;之后，奇异值逐渐增大并且存在一定的波动性，SV最大值约为2.7左右，此时认为起升减速箱处于轻微退化状态;约第940个滑动窗之后，SV值迅速增至区间[3.5，5.2]之间，并出现一定的波动性。此时认为起升减速箱处于严重退化状态;约第2000个滑动窗之后，设备再次出现退化过程，SV取值再次增加，最大值达到6.1左右，并出现一定的波动，此时认为起升减速箱处于失效阶段;在约第2450个滑动窗时，齿轮箱进行了检修，并更换了损坏的轴承。设备经过一定阶段的磨合之后，SV取值快速下降，回落到运行初期的水平。

图11对比分析了窗口宽度参数w对奇异值SV的影响。可以看出，窗口宽度能够决定对于随机冲击成分的滤除能力。宽度越小，曲线的随机波动越明显，变化细节反映越充分;宽度越大，主趋势反映越明显。因此，可以根据实际需求设置恰当的滑动窗口宽度。

4.3 轨道铰点在线退化特征提取

采用轨道铰点全寿命数据集Dataset2验证本方法的有效性。设置分析周期T=500，Dataset2共划分为1272组G_i（i=1，2，…，1272）。分别计算每组的改进符号序列熵ISSE，阈值因子a设置为G₁标准偏差的2倍。轨道铰点全寿命演化进程中的ISSE特征序列I_j如圖12（a）所示。退化程度越深，ISSE取值呈现逐渐增大的趋势，同时也呈现了一定的阶段性。由于振动有效值序列中较强的随机冲击，使得ISSE特征曲线中也伴随有明显的随机波动，影响了对于性能退化趋势的精确跟踪。图12（b）对比了改进之前的SSE特征序列，该曲线随机波动性强，且并未体现出单调变化的主趋势。

采用滑動窗口?奇异值分解的方法提取奇异值。设置滑动窗口宽度w=60，步长s=1。对每组滑动窗口内的ISSE序列进行奇异值分解，得到的奇异值演化曲线如图13所示。可以看出，奇异值演化曲线准确地反映了轨道铰点的退化进程，阶段性较弱，但能够清晰地表现出性能退化的进程。第35组窗口之前，奇异值基本稳定在0.5左右。之后迅速增大，说明轨道铰点位置出现了一定的性能退化，并且不断加深，并在第382个窗口附近达到4.2左右。之后，奇异值保持稳定，并存在一些上下波动。最大值达到4.65，此阶段维持了较长的时间。约第1161窗口左右，轨道铰点进行了检修，并更换了磨损的垫板。维修完成后，轨道铰点结构不需要磨合的过程，奇异值迅速下降至正常状态。

5 结 论

研究并提出基于改进符号序列熵与滑动窗口奇异值的在线退化特征提取方法。采用起升减速箱和轨道铰点的全寿命状态监测信号进行了方法的验证。得到以下结论：

（1）改进的符号序列熵算法引入了阈值因子，既保留了序列方向变化的信息，又刻画了“粗粒化”的幅值变化信息。与改进前的符号序列熵相比，能够更有效地滤出随机冲击的影响，挖掘得到信号中蕴含的复杂度信息。

（2）采用滑动窗奇异值分解的方式能够有效滤除ISSE序列中的随机波动影响，提高退化特征的稳定性，得到的滑动窗奇异值能够刻画起升减速箱和轨道铰点的性能退化程度。

（3）退化程度越深，退化特征取值越大，并且退化特征曲线具有一定的阶段性。如何确定不同阶段的阈值和边界，将是下一步的研究重点。

参考文献：

[1]        Starykov M， Van Hoorn F. The influence of a quay crane sea transportation on its further exploitation[J]. Transport， 2018， 32（2）： 536-542.

[2]        Liu C， Zhang H， Xie Z， et al. Combined forecasting method of dissolved gases concentration and its application in condition-based maintenance[J]. IEEE Transactions on Power Delivery， 2019， 34（4）： 1269-1279.

[3]        张 龙，黄文艺，熊国良，等.基于多域特征与高斯混合模型的滚动轴承性能退化评估[J].中国机械工程，2014，25（22）： 3066-3072.

Zhang Long， Huang Wenyi， Xiong Guoliang， et al. Assessment of rouing bearing performance degradation using Gauss mixture model and multi-domain features[J]. China Mechanical Engineering， 2014， 25（22）： 3066-3072.

[4]        Hong S， Zhou Z， Zio E， et al. Condition assessment for the performance degradation of bearing based on a combinatorial feature extraction method[J]. Digital Signal Processing， 2014， 27： 159-166.

[5]        Wu J， Wu C， Cao S， et al. Degradation data-driven time-to-failure prognostics approach for rolling element bearings in electrical machines[J]. IEEE Transactions on Industrial Electronics， 2019， 66（1）： 529-539.

[6]        倪祥龙，赵建民，陈吉潮，等.行星变速箱退化特征参数提取方法[J].振动.测试与诊断，2019，39（2）： 359-368.

Ni Xianglong， Zhao Jianmin， Chen Jichao， et al. Method of planetary gearbox degradation feature extraction[J]. Journal of Vibration， Measurement & Diagnosis， 2019， 39（2）， 359-368.

[7]        Araneo R， Attolini G， Celozzi S， et al. Time-domain shielding performance of enclosures：A comparison of different global approaches[J]. IEEE Transactions on Electromagnetic Compatibility， 2016， 58（2）： 434-441.

[8]        Randall R B， Antoni J. Rolling element bearing diagnostics——A tutorial[J]. Mechanical Systems & Signal Processing， 2011， 25（2）： 485-520.

[9]        程道来，贾玉琛，潘玉娜.基于S时频熵的球轴承性能退化特征指标提取方法[J].轴承，2019，（4）： 59-62.

Cheng Daolai， Jia Yuchen， Pan Yuna. Extraction mothod for performance degradation characteristic indexes of ball bearings based on S-time-frequency entropy[J]. Bearing， 2019， （4）： 59-62.

[10]      王志霞，郭 利.基于熵特征与HMM的滚动轴承退化状态识别[J].组合机床与自动化加工技术，2018，（7）：64-68.

Wang Zhixia， Guo Li. Degradation state recognition of rolling based on entropy and HMM[J]. Modular Machine Tool & Automatic Manufacturing Technique， 2018， （7）： 64-68.

[11]      李凌均，金 兵，马艳丽，等.基于MEMD与MMSE的滚动轴承退化特征提取方法[J].郑州大学学报（工学版），2018，39（4）： 86-91.

Li Lingjun， Jin Bing， Ma Yanli， et al. The method of degradation feature extraction of rolling bearing on MEMD and multivariate multiscale entropy[J]. Journal of Zhengzhou Unversity （Engineering Science）， 2018， 39（4）， 86-91.

[12]      Gao Y， Villecco F， Li M， et al. Multi-scale permutation entropy based on improved LMD and HMM for rolling bearing diagnosis[J]. Entropy， 2017， 19（4）： 176-182.

[13]      辛 怡，赵一璋，母远慧.基于Poincaré散点图和符号动力学的心电分析方法[J].北京理工大学学报，2017，37（10）： 1084-1089.

Xin Yi， Zhao Yizhang， Mu Yuanhui. ECG feature analysis based on Poincaré plot and symbolic dynamics[J]. Transactions of Beijing Institute of Technology， 2017， 37（10）， 1084-1089.

[14]      李红利，王 江，邓 斌，等.癫痫脑电的互信息和同步性分析[J].计算机工程与应用，2013，49（6）： 19-22.

Li Hongli， Wang Jiang， Deng Bin， et al. Analysis of mutual information and synchronism for epileplic EEG signals[J]. Computer Engineering and Applications， 2013， 49（6）： 19-22.

[15]      杜 飞，王世通，戴加飞，等.少年与中年脑电信号的多尺度符号序列熵分析[J].北京生物医学工程，2016，35（6）： 599-603.

Du Fei， Wang Shitong， Dai Jiafei， et al. Multiscale sign series entropy analysis based on the young and middle-aged electroencephalogram[J]. Beijing Biomedical Engineering， 2016， 35（6）： 509-603.

[16]      卞春華，马千里，司俊峰，等. 短时心率变异符号序列的熵分析方法[J]. 科学通报，2009，54（24）：340-344.

[17]      潘峥嵘，谯自健，张 宁.基于符号序列熵的自适应随机共振的微弱信号检测[J].计量学报，2015，36（5）： 496-500.

Pan Zhengrong， Qiao Zijian， Zhang Ning. Weak signal detection of adaptive stochastic based on Shannon entropy of symbolic series[J]. Acta Metrologica Sinica， 2015， 36（5）： 496-500.

[18]      Zhang J， Zhang P， Hua C， et al. Improved method for bearing AE signal denoising based on K-SVD algorithms[J]. Journal of Vibration & Shock， 2017， 36（21）： 150-156.

[19]      唐 刚，李建霞，胡 雄.准确近似聚类算法及其在岸桥拉杆状态监测中的应用[J].东华大学学报（自然科学版），2018，44（4）： 590-594.

Tang Gang， Li Jianxia， Hu Xiong. Accurate approximate clustering algorithm and its application in the state monitoring of crane[J]. Journal of Donghua Unversity （Natural Science）， 2018， 44（4）： 590-594.

Abstract： In order to track performance degradation condition of shore bridge key components accurately， an online degradation feature extraction method based on improved symbol sequence entropy and sliding window singular value is proposed. In view of the special character of the shore bridge and the frequent random vibration impact， a threshold factor is introduced and the sequence symbolization method is improved. The information of the amplitude change of the “coarse grain” is also taken into account while retaining the direction information， thereby， improving the ability of filtering impact and characterizing signal complexity. The improved symbol sequence entropy of the vibration signal is calculated online， combining with the sliding window method， the singular value of the improved sequence entropy sequence is extracted cyclically， which is used as the online degradation feature of the key components of the shore bridge. The full-life vibration signals from the lifting gearbox and track hinge point of Shanghai Port Container Terminal are used to analyze the results. The results show that the sliding window singular value can describe the performance degradation degree of the lifting gearbox and track hinge point. The deeper the degradation degree is， the larger the singular value is. It has the advantages of stable and fast calculation. It can also lay a method foundation for accurately tracking and evaluating health status.

Key words： signal processing; shore bridge; degradation feature extraction; symbol sequence entropy; singular value decomposition

作者簡介： 王 微（1983?），女，讲师。电话：（021）38282600;E-mail：wwang@shmtu.edu.cn