强背景噪声振动信号中滚动轴承故障冲击特征提取

刘湘楠　赵学智　上官文斌

摘要： 针对机械早期故障引起的冲击特征微弱，易受强背景信号和噪声的干扰而难以提取的问题，提出一种奇异值分解（Singular Value Decomposition， SVD）差分谱与S变换相结合的微弱冲击特征提取方法。将原始信号构造成Hankel矩阵，采用SVD对重构矩阵进行分解;利用奇异值差分谱确定降噪阶次进行降噪;采用S变换对降噪后的信号进行时频分析，提取信号中的微弱冲击特征信息。通过数值仿真和实际轴承故障数据的对比，表明该方法可有效辨别轴承振动信号中故障引起的早期微弱冲击特征，为轴承故障诊断提供先验信息。

关键词： 故障诊断; 滚动轴承; 冲击特征; 奇异值分解; S变换

中图分类号： TH165⁺.3; TH133.33; TN911.7    文献标志码： A    文章编号： 1004-4523（2021）01-0202-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.01.023

引 言

滚动轴承是旋转机械设备中广泛使用的零部件之一，也是旋转机械最主要的故障来源之一^[1]。在实际运行过程中由于工况复杂、过载、安装精度差及润滑不良等原因，滚动轴承外圈、滚动体及内圈等部件容易发生故障，进而影响机械系统整体运行的安全性和可靠性^[2]。滚动轴承产生故障时，工作过程中会产生突变的冲击力，该冲击信号的频率即为损伤点撞击轴承元件的频率^[3]。滚动轴承振动信号蕴含了大量的运行状态信息，表现为非线性和非平稳性的调制信号，对振动信号进行分析，可有效获取振动信号中所包含的轴承故障引起的冲击特征信息。但由于旋转机械设备结构复杂以及工作条件的多样性，各种激励源产生的信号相互耦合，导致滚动轴承故障引起的冲击特征常常淹没在强背景信号和噪声中，比较难以识别，特别是早期故障信号，在强噪声背景下轴承振动信号故障冲击特征信息微弱，更加难以提取^[4?5]。因此，如何实现强噪声背景下轴承振动信号故障冲击特征信息的有效提取，对旋转机械设备正常运行具有重要意义。

传统的信号特征信息提取方法中，傅里叶变换由于缺乏时间、频率的定位功能，在非平稳信号分析中有很大的局限性。随着短时傅里叶变换（STFT）、连续小波变换（CWT）等时频分析理论的逐渐发展， 为快速精确提取非平稳信号时频特征提供了新的途径。但现有的时频分析方法都具有一定的局限性，如：STFT其时间窗口的大小、形状都是固定的，与频率无关，无法同时获得精准的时刻和频率^[6]。CWT结果受Heisenberg不确定性原理和小波基函数的影响，在实际处理中难以找到合适的小波基函数，而且CWT得到的小波系数谱会发生能量泄漏，使得瞬时频率能量分布被模糊化^[7]。S变换是一种新的时频分析方法，克服了STFT窗函数以及CWT基函数固定不变的缺点，是一种高效的自适应信号时频分析方法，适合分析非线性和非平稳信号，通过调整参数可以改变信号的时频分辨率，以便得到冲击信号在时频域中良好的能量集中性，并且其逆变换完全无损^[8?9]。Pinnegar等^[10]研究表明S变换在无噪声干扰下能够显著提高时频分辨率，但在强背景噪声时会出现时频模糊的特点，难以有效识别信号中的冲击特征信息。由于现场采集的轴承故障振动信号中往往存在着较强的环境噪声及其他振动源干扰，会严重影响S变换的时频分析精度，因此，在利用S变换对轴承振动信号故障冲击特征信息进行提取前，对信号进行降噪处理是十分必要的。

奇异值分解作为一种非线性信号降噪方法，在轴承振动信号^[11?12]、语音信号^[13]、电荷放电信号^[14]等不同性质信号降噪方面有着广泛的应用。利用SVD对信号进行降噪的关键在于如何利用信号构造合适的矩阵以及确定有效奇异值的个数。目前SVD降噪中应用最广泛的矩阵形式是Hankel矩阵，采用Hankel矩阵的突出特点就是能够消除信号中的噪声^[15?17]。另外，信号非零奇异值中有效奇异值个数的选取决定着降噪效果的好坏，奇异值个数选取过少容易导致信號有用信息丢失，有时甚至会导致信号波形出现畸变，而选取过多又会造成信号降噪效果较差^[18]。赵学智等^[19]研究表明，根据奇异值差分谱的峰值位置可以准确地确定有效奇异值的个数。

基于以上原因，本文提出一种基于SVD差分谱和S变换相结合的微弱故障冲击特征信息提取方法。该方法将SVD差分谱作为S变换的前置滤波单元，对信号滤波降噪后再进行S变换时频分析，根据信号时频谱图获取故障冲击特征。最后，将该方法应用于轴承故障信号分析，成功提取出其故障冲击特征，获得了较为满意的结果。

1 理论分析

3.1 内圈故障分析

结合旋转机械设备的实际工况，滚动轴承故障振动信号通常易受强背景噪声干扰，因此，本文在轴承内圈故障振动信号中添加信噪比为0的高斯白噪声，以模拟工程实际。图9为加噪前后轴承内圈故障振动信号波形图。

由图9（b）可知，加噪后轴承内圈故障引起的冲击特征微弱，从时域信号波形图中已无法获取冲击特征。本文采用STFT，CWT，S变换分别对加噪前后轴承内圈故障振动信号进行时频分析，其中CWT所用的小波为Morlet小波，尺度为64。

图10为内圈故障振动信号加噪前后时频谱图。由图10（b）可知，当轴承内圈故障引起的冲击特征呈现出强噪声背景下特征微弱时，采用STFT， CWT和S变换3种时频分析方法均难以有效获取内圈故障引起的冲击特征。为准确识别强噪声背景下轴承内圈故障引起的冲击特征，需对信号进行降噪预处理。

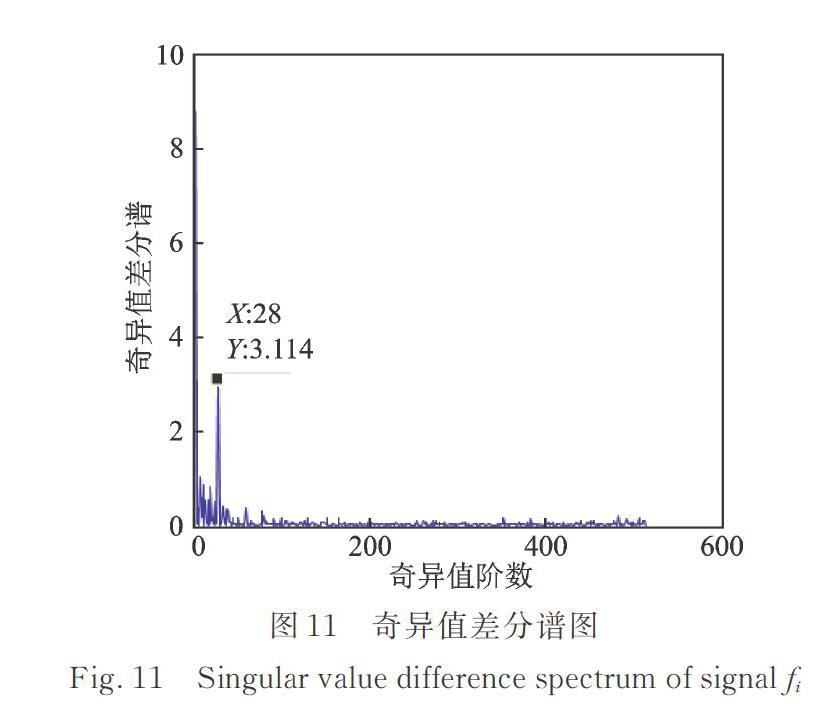
将加噪的轴承内圈故障振动信号构造成512×513阶Hankel矩阵，采用SVD对矩阵进行分解，根据奇异值差分谱选取有效奇异值。 图11为信号的奇异值差分谱图，将28个有效奇异值对应的信号组合重构，获得降噪后的轴承内圈故障振动信号。

采用STFT，CWT，SST三种方法对SVD差分谱降噪后的轴承内圈故障振动信号进行时频分析，图12为内圈故障振动信号降噪后时频谱图。

由图12可知，利用本文所提出的方法对降噪后的内圈故障振动信号进行时频分析，可有效获取微弱冲击特征。整个时间轴上，频率轴约3000 Hz处出现明显的周期性冲击特性，其周期约为0.006253 s，对应的频率为159.92 Hz，与内圈故障频率157.94 Hz基本一致。

对采用SVD差分谱降噪后的内圈故障振动信号时频谱进行S逆变换，提取轴承内圈故障振动信号中的时域冲击特征，如图13所示。

对比图9（a）和13可知，本方法所提取的内圈故障引起的冲击特征不可避免地出现一定的变形和失真，但作为最重要信息的冲击特征出现频率，则可以完全有效地提取出来。

3.2 外圈故障分析

将本文所提出的方法应用于滚动轴承外圈单点故障振动信号特征提取，图14为轴承外圈故障振动信号波形图。

由图14可知，轴承外圈故障引起的冲击特征在强噪声背景下特征微弱，由信号时域图难以获取信号冲击特征。

将外圈故障振动信号构造成512×513阶Hankel矩阵，采用SVD对矩阵进行分解，根据奇异值差分谱选取有效奇异值。图15为信号的奇异值差分谱图，将14个有效奇异值对应的信号组合重构，获得降噪后的外圈故障振动信号。

采用S变换对降噪后外圈故障振动信号进行时频分析。图16为降噪后滚动体故障振动信号的S变换时频谱图。

由图16可知，采用S变换对降噪后的外圈故障振动信号进行时频分析，可有效获取微弱冲击特征。整个时间轴上，频率轴约3500 Hz处出现明显的周期性冲击特性，其周期约为0.009667 s，对应的频率为103.44 Hz，与外圈故障频率104.57 Hz基本一致。

对采用SVD差分谱降噪后的时频谱进行S逆变换，提取轴承外圈故障振动信号中的时域冲击特征，如图17所示。

由图17可知，采用本文方法能实现强噪声背景下轴承外圈故障引起的冲击特征信息。

综上所述，实验模拟的轴承内圈分析结果验证了本文方法对强噪声背景下故障微弱冲击特征提取的有效性。在此基础上，将本文所提出的方法应用于轴承外圈故障振动信号进行分析，结果表明，该方法能够有效提取外圈故障引起的冲击特征，实现了对滚动轴承的故障诊断。

4 结 论

（1） 提出了一种基于SVD差分谱和SST相结合的信号弱冲击特征提取方法。首先将原始信号构造成Hankel矩阵，利用SVD对矩阵进行分解;再利用差分谱理论确定降噪阶次进行降噪，最后，采用S变换对降噪后的信号进行时频分析，实现了信号弱冲击特征的有效提取;

（2） 对比分析了STFT，CWT，S变换3种方法对信号冲击特征的识别能力，结果表明： STFT无法识别信号弱冲击特征;CWT能识别信号弱冲击特征，但其分辨率及时频聚集性不如S变换;S变换提高了时频聚集性，能够有效识别信号中的冲击特征。

参考文献：

[1]        El-Thalji I， Jantunen E. A summary of fault modelling and predictive health monitoring of rolling element bearings[J]. Mechanical Systems & Signal Processing， 2015，60-61（1）： 252-272.

[2]        Dyba?a J. Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal[J]. Applied Acoustics， 2014， 77（3）：195-203.

[3]        唐貴基， 蔡 伟. 应用小波包和包络分析的滚动轴承故障 诊断[J]. 振动、测试与诊断， 2009， 29（2）： 201-204.

Tang Guiji， Cai Wei. Rolling bearings fault diagnosis by using wavelet packet and envelope analysis[J]. Journal of Vibration， Measurement & Diagnosis， 2009， 29（2）： 201-204.

[4]        陈志新， 徐金梧， 杨德斌. 基于复小波块阈值的降噪方 法及其在机械故障诊断中的应用[J]. 机械工程学报， 2007， 43（6）：200-204.

Chen Zhixin， Xu Jinwu， Yang Debin. Denoising method of block thresholding based on DT-CWT and its applocation in mechanical fault diagnosis[J]. Journal of Mechanical Engineering， 2007， 43（6）：200-204.

[5]        李富才， 何正嘉， 陳 进. 小波域相关滤波法及其早期故 障预示应用[J]. 振动工程学报， 2005，18（2）：145-148.

Li Fucai， He Zhengjia， Chen Jin. Wavelet transform doma domain correlation filter and its application in incipient fault prognosis [J]. Journal of Vibration Engineering， 2005，18（2）：145-148.

[6]        刘义亚， 李 可， 陈 鹏. 基于同步压缩小波变换的滚动轴承故障诊断[J]. 中国机械工程， 2018，29（5）： 585-590.

Liu Yiya， Li Ke， Chen Peng. Fault diagnosis for rolling bearings based on synchrosqueezing wavelet transform[J]. China Mechanical Engineering， 2018， 29（5）： 585-590.

[7]        Sinha S， Routh P S， Anno P D， et al. Spectral decomposition of seismic data with continuous-wavelet transform[J]. Geophysics， 2008， 70（6）：19-25.

[8]        Pinnegar C R ， Mansinha L . The S-transform with windows of arbitrary and varying shape[J]. Geophysics， 2003， 68（1）：381-385.

[9]        Kazemi K， Amirian M， Dehghani M J. The S-transform using a new window to improve frequency and time resolutions[J]. Signal， Image and Video Processing， 2014， 8（3）：533-541.

[10]      Pinnegar C R， Mansinha L. Time-local spectral analysis for non-stationary time series： The S-transform for noisy signals[J]. Fluctuation & Noise Letters， 2012，3（3）：L357-L364.

[11]      王建国， 李 健， 万旭东. 基于奇异值分解和局域均值 分解的滚动轴承故障特征提取方法[J]. 机械工程学报，2015，（3）：104-110.

Wang Jianguo， Li Jian， Wang Xudong. Fault feature extraction method of rolling bearings based on singular value decomposition and local mean decomposition [J]. Journal of Mechanical Engineering， 2015，（3）：104-110.

[12]      Golafshan R， Sanliturk K Y. SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults[J]. Mechanical Systems & Signal Processing， 2016， （70?71）：36-50.

[13]      Zheng C， Peng R， Li J， et al. A constrained MMSE LP residual estimator for speech dereverberation in noisy environments[J]. IEEE Signal Processing Letters， 2014， 21（12）：1462-1466.

[14]      Ashtiani M B， Shahrtash S M. Partial discharge de-noising employing adaptive singular value decomposition[J]. IEEE Transactions on Dielectrics and Electrical Insulation， 2014， 21（2）：775-782.

[15]      李 华， 刘 韬， 伍 星，等. 基于SVD和熵优化频带熵的滚 动轴承故障诊断研究[J]. 振动工程学报， 2018， 31 （2）：180-186.

Li Hua， Liu Tao，Wu Xing， et al.Research on fault diagnosis of rolling bearing based on SVD and optimized frequency band entropy by entropy[J]. Journal of Vibration Engineering，2018，31（2）：180-186.

[16]      胥永刚，张志新，马朝永，等. 改进奇异谱分解及其在轴承故障诊断中的应用[J]. 振动工程学报， 2019， 32 （3）： 540-547.

Xu Yonggang， Zhang Zhixin，Ma Chaoyong， et al. Improved singular spectrum decomposition and its application in bearing fault diagnosis[J]，Journal of Vibration Engineering，2019， 32 （3）： 540-547.

[17]      王 超， 孔凡让， 黄伟国，等. 改进的奇异值分解在轴承故障诊断中的应用[J]. 振动工程学报， 2014， 27（2）： 296-303.

Wang Chao， Kong Fanrang， Huang Weiguo，et al. Application of improved singular value decomposition in bearing fault diagnosis[J].Journal of Vibration Engineering，2014， 27（2）： 296-303.

[18]      赵学智， 叶邦彦， 陈统坚. 奇异值差分谱理论及其在 车床主軸箱故障诊断中的应用[J]. 机械工程学报， 2010， 46（1）：100-108.

Zhao Xuezhi， Ye Bangyan， Chen Tongjian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J]. Journal of Mechanical Engineering， 2010， 46（1）：100-108.

[19]      赵学智， 叶邦彦， 陈统坚. 基于小波—奇异值分解差 分谱的弱故障特征提取方法[J]. 机械工程学报， 2012， 48（7）：37-48.

Zhao Xuezhi， Ye Bangyan， Chen Tongjian. Extraction method of faint fault feature based on wavelet-SVD difference spectrum[J]. Journal of Mechanical Engineering， 2012， 48（7）：37-48.

[20]      吕志民， 张武军， 徐金梧， 等. 基于奇异谱的降噪方 法及其在故障诊断技术中的应用[J]. 机械工程学报， 1999， 35（3）：85-88.

Lü Zhiming， Zhang Wujun， Xu Jinwu， et al. A noise reduction method based singular spectrum and its application in machine fault diagnosis[J]. Journal of Mechanical Engineering， 1999， 35（3）：85-88.

[21]      杨文献， 姜节胜. 机械信号奇异熵研究[J]. 机械工程 学报， 2000， 36（12）：9-13.

Yang Wenxian， Jiang Jiesheng. Research on mechanical signal singular entropy[J]. Journal of Mechanical Engineering， 2000， 36（12）：9-13.

[22]      何 田， 刘献栋， 李其汉. 噪声背景下检测突变信息的 奇异值分解技术[J]. 振动工程学报， 2006， 19（3）：399-403.

He Tian， Liu Xiandong， Li Qihan. An improved method singularity value of detecting abrupt information based on decomposition in noise background [J]. Journal of Vibration Engineering， 2006， 19（3）： 399-403.

[23]      Stockwell R G， Mansinha L， Lowe R P. Localization of the complex spectrum： The S transform[J]. IEEE Transactions on Signal Processing， 2002， 44（4）：998-1001.

Abstract： Aiming at the problem that the impact of early mechanical failure is weak and it is difficult to extract due to strong background signal and noise interference， a weak impact feature extraction method combining singular value decomposition （SVD） differential spectrum and S?transform is proposed. The original signal is constructed into a Hankel matrix， and the reconstruction matrix is decomposed by SVD. The noise reduction order is determined by singular value difference spectrum for noise reduction. The S-transformation is used to analyze the time-frequency of the denoised signal， the weak impact characteristic information of the signal is extracted. The comparison between numerical simulation and actual bearing fault data shows that the method can effectively distinguish the early weak shock characteristics caused by faults in the bearing vibration signal. It can provide a priori information for the bearing fault diagnosis.

Key words： fault diagnosis; rolling bearing; impact feature; singular value decomposition; S?transform

作者简介： 刘湘楠（1992?），男，博士研究生。电话：16607319453;E-mail：lxn920613@163.com