低振动旋翼桨尖代理优化设计
邓旭东 高乐 邓景辉


摘要: 为探索直升机低振动旋翼的工程设计方法,将代理优化与旋翼气弹耦合分析相结合,开展了旋翼桨尖几何外形设计,推导了非平直桨叶气弹动力学方程,训练了旋翼功率、模态阻尼以及振动载荷预测的Kriging代理模型。以气动性能与气弹稳定性为约束,以桨毂振动载荷最小化为目标,采用自适应加点准则设计了优化流程。以某旋翼为例,计算了其气动性能与振动载荷,通过与试验结果对比,验证了气弹模型的有效性。对该基准旋翼0.9R?1.0R(R为旋翼半径)桨叶段的后掠、下反以及扭转分布进行了优化设计,结果表明,基于样本点最小间距的自适应加点准则能够实现目标函数与约束函数代理精度的同步提升。通过优化结果可行性分析,得到了一种“双后掠+上、下反”桨尖构型,旋翼桨毂振动载荷降低了25%。
关键词: 旋翼; 桨尖; 气弹分析; 减振; 代理优化
中图分类号: V275+.1 文獻标志码: A 文章编号: 1004-4523(2021)01-0108-08
DOI:10.16385/j.cnki.issn.1004-4523.2021.01.012
引 言
直升机旋翼工作中,前行桨尖区域相对气流速度高,流场在时间与空间两个维度上变化剧烈,对旋翼整体性能有显著影响,因此改善桨尖设计是提升旋翼气动效率的有效途径,而且代价最小。
早期的旋翼桨尖被简单处理为弧形或矩形,到了20世纪70年代,复合材料逐步取代金属成为桨叶主要材料,为桨叶外形设计提供了更多可能性,欧美直升机厂商开始寻求通过改进桨尖形状来提高旋翼性能的方法。最初的思路是采用桨尖后掠与尖削设计来抑制高马赫数下的气流压缩效应,降低型阻功率,如西科斯基公司UH?60直升机旋翼采用的直线后掠桨尖,欧洲直升机公司的抛物线后掠桨尖,在提升旋翼气动性能方面均有良好收效[1]。桨尖后掠导致剖面重心与气动中心向后缘移动,削弱了桨叶气弹稳定性,须采取前突、前掠等补偿措施,令桨叶整体气动中心靠近变距轴线;前飞状态下桨尖后掠会产生明显的1Ω(Ω为旋翼转速)桨叶扭矩,使旋翼操纵载荷变大,下反设计恰好能减小这一操纵载荷,同时能令桨尖脱出涡向下移动,降低桨?涡干扰强度,有利于旋翼降噪。基于以上考虑,当前先进几何外形桨叶通常采用“前突、后掠、尖削、下反”组合的桨尖设计,如德?法合作研制的Blue Edge桨叶[2]、英国的BERP桨叶[3],已经在量产机型上成功应用。
非平直桨尖导致桨叶挥?摆?扭自由度产生强烈的运动耦合,对气弹响应影响显著。Celi[4]基于伽辽金有限单元法建立了非平直桨叶运动控制方程,揭示了后掠、下反所引起的桨叶运动自由度之间气动弹性耦合机理;Benquet等[5]系统分析了无铰旋翼前飞状态下桨尖后掠、下反对旋翼气弹响应的影响,结果表明5°的桨尖后掠就能使桨毂垂向动载荷降低14%。随着计算机技术发展,以CAMRAD,UMARC,2GCHAS,DYMORE为代表的直升机综合分析软件逐步发展完善,旋翼CFD技术也取得长足进步,研究人员开始采用更加精细的旋翼气动与结构模型,如CSD/CFD耦合模型,以提升性能或降低振动为目标,对桨叶气动外形、内部构造等详细设计特征进行了优化研究[6?13]。
随着设计变量增多,采用精细模型的优化运算规模愈发庞大,代理优化通过将运算规模较大的复杂目标函数、约束函数的代理模型作为算法直接调用对象,降低了复杂模型调用次数。Glaz等[14]、Ganguli[15]以最小化桨毂振动为目标,采用代理模型对桨叶剖面参数进行了优化;Leon等[16]、Sun等[17]、Andrew等[18]采用代理优化方法对桨叶气动外形进行了设计,提升了旋翼气动性能。在中国,代理优化方法在翼型设计方面应用较为成熟。韩忠华[19]概述了Kriging代理优化理论和算法最新进展,对优化机制与框架进行详细阐述,并讨论了影响优化模型鲁棒性与效率的若干关键问题,对研究代理优化在航空领域的应用具有重要参考价值;韩少强等[20]、宋超等[21]、王晓锋等[22]、许瑞飞等[23]、孙俊峰等[24]基于Kriging代理模型对翼型进行了优化设计研究,从而实现增升减阻;李耀辉[25]研究了基于Kriging模型的全局近似与优化方法,对代理建模、样本选取、优化流程、并行算法等技术细节进行了梳理。
直升机旋翼设计是一类多学科交叉的系统工程问题,需要综合考虑气动性能、动力稳定性、结构强度、以及振动响应等多个要素。中国型号研制中基本按照“气动外形设计、结构设计、动力学评估”等几个环节依次进行,气动外形与结构设计通常独立开展,忽略了重要的气弹耦合特性,设计迭代高度依赖工程经验,难以捕捉到最优设计点。基于高置信度CSD/CFD耦合模型的优化设计是当前直升机旋翼学术研究的前沿,但其工程应用仍面临困难,旋翼CFD网格自适应变形、大规模气动与结构数据交互等难点并未完全攻克,计算资源消耗巨大。在这种情况下,发展一种兼备全局寻优能力与高效迭代能力的气动弹性耦合设计方法,对直升机旋翼工程设计有重要意义。
本文以直升机旋翼减振设计为背景,在旋翼气弹耦合分析的基础上应用代理优化,开展基于Kriging模型的旋翼桨尖几何外形优化研究。针对直升机典型的稳态前飞状态,设计了以桨毂减振为目标,以气动性能与气弹稳定性为约束的旋翼桨尖优化设计流程,采用自適应加点准则实现目标函数与约束函数代理精度的同步提升。随后对某模型旋翼进行了算例分析,结果表明本文方法在旋翼性能与振动载荷预测方面可信度较高。通过对桨尖段后掠、下反以及扭转分布优化设计,得到了一种“双后掠+上、下反”桨尖构型,在不削弱气动性能与气弹稳定性的前提下,降低旋翼振动载荷25%。
1 旋翼气弹耦合模型
旋翼气弹耦合模型是优化设计的基础,随着仿真技术进步,以三维CSD/CFD全耦合模型为代表的高精度数值方法已成为学术研究的热点。尽管CSD/CFD耦合模型能够准确捕获旋翼流场与结构变形的非线性、非定常效应,但导致其求解不收敛的因素复杂,运行效率低,若无高性能并行计算能力支持,难以适应优化运算的大量迭代与频繁参数调整。相比之下,基于梁模型与叶素理论的旋翼气弹耦合方法较为成熟,其可靠性得到了充分验证,结合翼型非定常气动与自由尾迹模型,能够对影响旋翼性能与载荷的主要流动特性进行模拟,精度与效率同工程优化需求最为契合,因此本文采用该方法进行气弹耦合分析。
3 算例与分析
3.1 基准旋翼性能与载荷
本文基准旋翼为5桨叶球柔式旋翼,该旋翼在中国空气动力研究与发展中心8 m×6 m风洞中完成了吹风试验。采用本文方法计算其悬停与前飞状态下的性能与振动载荷,并同试验结果对比。
旋翼气动性能可由需用功率衡量。悬停状态下产生同样拉力所消耗的功率越小,悬停效率越高。对于前飞,在给定风速、拉力状态下,所需功率越小前飞性能越好。
图3中CT,CP分别代表旋翼拉力与功率系数。图3(a)为悬停状态拉力?功率曲线,旋翼转速Ω=1026 r/min;图3(b)为前飞状态功率系数随风速变化曲线,转速1033 r/min,拉力系数CT=0.0075。与实测值相比,悬停气动性能计算误差不超过7%;前飞气动性能不超过14%。
旋翼桨毂载荷在试验中主要由天平测量,但天平对高阶动载荷测量精度不高,需要专门的动态标定。考虑到桨毂载荷是各片桨叶的集成,一般通过应变片测量桨叶剖面动载荷,间接评估旋翼振动载荷。图4给出了前进比为0.2时桨根(0.205R)弯矩的计算值与实测值,图4(a),(b)分别为挥舞弯矩Mflap与摆振弯矩Mlag随方位角Azimuth变化曲线。
桨根载荷计算与实测相比,挥舞弯矩1/2峰?峰值相对误差为4.1%,摆振弯矩1/2峰?峰值相对误差为15.6%;计算值与实测值主要频率成分一致,1Ω低频载荷的幅值、相位吻合良好,高频载荷偏差也在可接受范围内。通过与悬停、风洞试验结果对比,表明本文所采用的旋翼气弹模型在性能预测方面具有较高精度,对旋翼动载荷预估可靠性良好,可用于旋翼桨尖几何外形优化研究。
3.2.2 优化迭代
采用拉丁超方实验设计生成20个初始样本,目标函数与非线性约束函数的Kriging建模采用1阶多项式回归函数及高斯相关函数,初始相关参数取0.5。采用梯度优化算法进行100次迭代,无量纲目标函数![]() 的变化历程如下。
的变化历程如下。
图6同时给出了旋翼气弹模型与Kriging模型在每个潜在最优点的目标函数估值,需要说明的是该潜在最优点此时并未更新到代理模型中。迭代30次以后,两条曲线逐步接近,表明Kriging模型在潜在最优点附近的代理精度显著提升,代理优化结果逐渐逼近气弹模型的最优解。
3.2.3 优化结果分析
受到非线性约束函数代理精度的影响,并不能保证每一个潜在最优点都可行,只有当潜在最优点同时满足所有约束时才是可行的。根据优化模型(13),可利用三个非线性函数的最大值![]() 作为可行性判断的依据,即
作为可行性判断的依据,即
图7给出了100个潜在最优点的Maxcon取值,共有25个可行点。从工程设计角度看,桨叶沿展向的弯折、扭转应平缓过渡,连续的前?后掠或上?下反交替变化在结构上是难以实现的。因此,采用相对简单的桨尖几何外形实现旋翼减振效果才是最佳方案,基于这一原则从25个可行点中选取一个最终设计点,优化结果如表3。
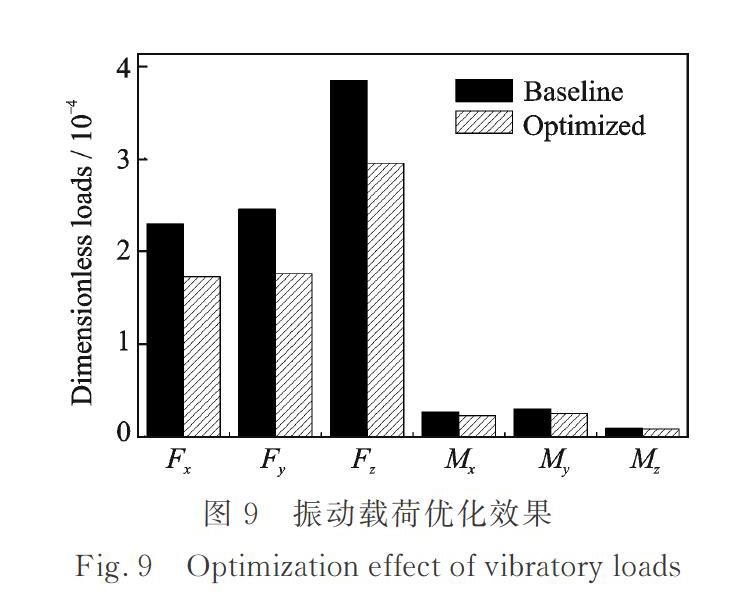
优化后目標函数相对于基准值降低了25%,1阶摆振阻尼略高于基准值,悬停及前飞功率系数均低于基准值,纵向周期变距![]() 略高于基准值。优化构型5Ω桨毂振动载荷(无量纲)同基准值对比如图9所示。
略高于基准值。优化构型5Ω桨毂振动载荷(无量纲)同基准值对比如图9所示。
可见,桨毂振动载荷6个分量均有所降低,力分量降幅均超过20%,力矩分量降幅也超过10%,达到了旋翼减振目的。
4 结 论
通过本文研究,得到如下几点结论:
1) 通过旋翼桨尖几何外形优化设计,得到了一种“双后掠+上、下反”的桨尖构型,在不削弱旋翼气动性能与气弹稳定性的情况下,使桨毂振动载荷降低了25%;
2) 将Kriging模型与自适应加点方法相结合,发展了一种面向减振的桨尖外形代理优化设计手段,可用于直升机旋翼这类复杂系统的快速工程设计。
参考文献:
[1] Brocklehurst A, Barakos G N. A review of helicopter rotor blade tip shapes[J]. Progress in Aerospace Sciences, 2013, 56: 35-74.
[2] Beaumier P,Wall B V D,Pengel K, et al. From ERATO basic research to the Blue EdgeTM rotor blade[C]. AHS International 72nd AHS Annual Forum and Technology Display, Florida, 2016.
[3] Rob Harrison, Simon Stacey, Bob Hansford. BERP IV the design, development and testing of an advanced rotor blade[C]. 64th AHS Annual Forum, Montreal,2008.
[4] Celi R. Aeroelasticity and structural optimization of helicopter rotor blades with swept tips[D]. Los Angeles: University of California, 1987.
[5] Philippe Benquet, Inderjit Chopra. Calculated dynamic response and loads for an advanced tip rotor in forward flight[C]. 15th European Rotorcraft Forum,Amsterdam, 1989.
[6] Yuan K A, Friedmann P P. Aeroelasticity and structural optimization of composite helicopter rotor blades with swept tips[R]. NASA-CR-4665, 1995.
[7] Joon W. Lim. Consideration of structural constraints in passive rotor blade design for improved performance[C]. 71st AHS Annual Forum,Virginia: 2015.
[8] Chae Sanghyun, Yee Kwanjung. Helicopter rotor shape optimization for the improvement of aeroacoustic performance in hover[J]. Journal of Aircraft, 2010, 47(5): 1770-1783.
[9] Le Pape A, Beaumier P. Numerical optimization of helicopter rotor aerodynamic performance in hover[C]. 29th European Rotorcraft Forum,Friedrichshafen, 2003.
[10] Droandi G, Gibertini G. Aerodynamic shape optimization of a proprotor and its validation by means of CFD and experiments[J]. The Aeronautical Journal, 2015, 119(1220): 1223-1251.
[11] Allen C B, Morris A M, Rendall T C S. CFD-based aerodynamic shape optimization of hovering rotors[C]. 27th AIAA Applied Aerodynamics Conference,San Antonio, 2009.
[12] Ganguli Ranjan, Chopra Inderjit. Aeroelastic tailoring of composite couplings and blade geometry of a helicopter rotor using optimization methods[J]. Journal of the American Helicopter Society,1997,42(3):218-228.
[13] Ku Jieun. A hybrid optimization scheme for helicopters with composite rotor blades[D]. Atlanta:Georgia Institute of Technology, 2007.
[14] Glaz B, Friedmann P P, Liu Li. Surrogate based optimization of helicopter rotor blades for vibration reduction in forward flight[C]. 47th AIAA Structures, Structural Dynamics, and Materials Conference, Newport, 2006.
[15] Ranjan Ganguli. Optimum design of a helicopter rotor for low vibration using aeroelastic analysis and response surface methods[J]. Journal of Sound and Vibration, 2002, 258(2): 327-344.
[16] Leon Enric Roca, Le Pape Aruaud. Concurrent aerodynamic optimization of rotor blades using a Nash game method[J]. Journal of the American Helicopter Society,2016,61(2):1-13.
[17] Sun Hyosung, Lee Soogab. Response surface approach to aerodynamic optimization design of helicopter rotor blade[J]. International Journal for Numerical Methods in Engineering, 2005, 64: 125-142.
[18] Booker Andrew J. A rigouous framework for optimization by sorrogates[R]. NASA-CR-208735, 1998.
[19] 韓忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报,2016,37(11): 3197-3225.
Han Z H. Kriging surrogate model and its application to design optimization:A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225.
[20] 韩少强,宋文萍,韩忠华,等. 基于梯度增强型Kriging模型的气动反设计方法[J]. 航空学报,2017,38(7): 120817.
Han S Q, Song W P, Han Z H, et al. Aerodynamic inverse design method based on gradient-enhanced Kriging model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 120817.
[21] 宋 超,杨旭东,宋文萍. 耦合梯度与分级Kriging模型的高效气动优化方法[J]. 航空学报,2016, 37(7): 2144-2155.
Song C, Yang X D, Song W P. Efficient aerodynamic optimization method using hierarchical Kriging model combined with gradient[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2144-2155.
[22] 王晓锋,席 光. 基于Kriging模型的翼型气动性能优化设计[J]. 航空学报,2005, 26(5): 545-549.
Wang X F, Xi G. Aerodynamic optimization design for airfoil based on Kriging model[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(5): 545-549.
[23] 许瑞飞,宋文萍,韩忠华. 改进Kriging模型在翼型气动优化设计中的应用研究[J]. 西北工业大学学报,2010, 28(4): 503-510.
Xu R F, Song W P, Han Z H. Application of improved Kriging-model-based optimization method in airfoil aerodynamic design[J]. Journal of Northwestern Polytechnical University, 2010, 28(4): 503-510.
[24] 孙俊峰,刘 刚,江 雄,等. 基于Kriging模型的旋翼翼型优化设计研究[J]. 空气动力学学报,2013, 31(4): 437-441.
Sun J F, Liu G, Jiang X, et al. Research of rotor airfoil design optimization based on the Kriging model[J]. Acta Aerodynamica Sinica, 2013, 31(4): 437-441.
[25] 李耀辉. 基于Kriging模型的全局近似与仿真优化方法[D]. 武汉:华中科技大学,2015.
Li Yaohui. The Kriging-based global approximation and simulation optimization methods[D].Wuhan:Huazhong University of Science & Technology, 2015.
Abstract: To establish efficient design methods of a helicopter rotor with low vibration, blade tip shape design is conducted through the combination of surrogated-based optimization and aeroelastic analysis. The aeroelastic equations of rotor blades with unstraight tips are derived. The Kriging surrogate-based models for predicting rotor power, modal damping and vibratory loads are trained. By using the aerodynamic performance and aeroelastic stability as constrains and minimizing the hub vibratory loads as objective, optimization strategy is developed based on an adaptive infill sampling criteria. Taking a scaled model rotor as an example, its performance and vibratory loads are calculated. The aeroelastic model validity is obtained through the comparison with experimental results. Design optimization of the blade sweep, droop and twist distribution from 0.9Rto 1.0Ris performed. The result indicates that the accuracy of the surrogates of objective function and constraint functions can be improved simultaneously with this adaptive infill sampling criteria based on minimum distance between two training samples. Through the feasibility analysis for optimization results, an optimized blade with double swept and negative/positive anhedral tip is obtained, which results in a 25% reduction of the vibratory hub loads.
Key words: rotor; blade tip; aeroelastic analysis; vibration reduction; surrogated-based optimization
作者簡介: 邓旭东(1986?),男,高级工程师。电话:13879875693;E?mail: dengxu2639@163.com

