大跨度连续梁拱桥多点多维地震响应分析

李小珍 ，杨得海 ，雷康宁 ，肖 林 ，戴胜勇

（1. 西南交通大学土木工程学院，四川 成都 610031；2. 中铁二院工程集团有限责任公司，四川 成都 610031）

连续梁拱桥作为一种新型大跨度组合结构桥梁，其主要特点是结构刚度大、动力性能稳定以及造型美观等. 与同等跨度连续梁桥相比，梁拱组合结构能减小跨中和支点处主梁的截面高度，使得桥梁的跨越能力与桥下净空得到提高. 然而，梁拱组合桥的跨径大、上部结构较重，是抗震的不利体系[1]. 随着桥梁跨度的大幅度提高，在进行地震动力响应分析时，地震动的空间变异性则不应忽视[2].

较多学者对非一致地震激励下桥梁结构的动力响应做了研究，李晰等[3]采用时程分析法系统地研究了脉冲型地震作用下钢管混凝土拱桥的抗震性能，并考虑了地震动的多维性，表明了随着脉冲周期的减小，地震动多维性对结构动力响应的影响会逐渐增大；王立宪等[4]分析了钢管混凝土拱桥的非一致地震响应，表明局部场地效应的影响大于行波效应和部分相干效应；Li等[5]基于振动台试验探究了地震动空间效应和碰撞效应对桥梁非弹性阶段动力响应的影响，表明地震动的空间变异性会对碰撞和塑性铰的发展产生影响，仅针对桥梁弹性阶段进行研究可能会高估桥梁可能发生的破坏；Bi等[6]对一座钢管混凝土拱桥在非一致地震激励下的动力响应作了研究，数值结果显示了在钢管混凝土拱桥的地震可靠性分析中，地震动多维输入以及空间变异性的影响不可忽视；马凯等[7]分析了一座大跨度漂浮体系斜拉桥在非一致地震激励下的易损性，表明一致激励会高估桥梁结构的抗震性能，失相干效应和场地效应对结构易损性的影响不能忽视. 综合而言，大量的研究都表明地震动的空间效应对桥梁结构地震反应具有较大的影响.

以往关于多点多维地震动的研究中，大多都是针对斜拉桥、悬索桥及拱桥等常规大跨度桥梁结构，而对于大跨度连续梁拱桥这一新型组合结构鲜有涉及. 本文基于某大跨度公路连续梁拱桥，人工合成非一致地震动，综合考虑行波效应、失相干效应以及场地效应等因素对连续梁拱桥动力响应的影响规律，并与一致地震动激励的结果进行对比分析.

1 桥梁模型

选取我国南方的一座大跨度连续梁拱桥为研究对象，其跨径布置为（56+139+56） m，桥梁的立面如图1所示. 大桥的主梁为变高度连续箱梁，中支点及跨中部分的箱梁高度分别为5.5 m和3.0 m. 大桥的拱肋采用哑铃形钢管混凝土截面，上下钢管及腹腔内灌注C55微膨胀混凝土，拱肋的计算跨度为139 m，设计矢高为27.8 m，矢跨比为1/5，拱轴线采用二次抛物线，为拱梁固结体系. 大桥共设14对连接拱肋与主梁的吊杆，采用PES（FD）7-109型低应力防腐拉索，外套复合不锈钢管.

图1 连续梁拱桥立面（单位：cm）Fig. 1 Elevation of the continuous beam-arch bridge (unit: cm)

桥梁的2# 与3# 主墩采用矩形实体墩，墩身的横桥向宽17.0 m，纵桥向宽3.8 m. 1# 与4# 边墩采用双柱式异型门墩，双柱间采用横梁连接，柱底截面尺寸为2.5 m × 2.5 m，柱顶截面尺寸为3.0 m × 3.5 m.桥址处场地类别为Ⅲ类，场地特征周期为0.40 s.

基于有限元软件OpenSEES，建立大桥的空间非线性分析模型. 采用弹性梁柱单元（elastic beam column）模拟主梁，拱肋及桥墩以基于位移插值的纤维梁柱单元（disp beam column）来详细模拟，吊杆以桁架单元（Truss）来模拟. 主梁与桥墩连接的支座采用零长度单元（zerolength）来模拟，并根据支座特性赋予6个自由度方向不同的材料强度，其中支座的竖向承载力为50000 kN，水平向非约束方向取其2%，水平约束方向取为20%，以单轴弹性材料（uniaxialmaterial elastic）模拟. 材料本构方面，为考虑材料非线性的影响，针对不同区域的混凝土选用不同的材料本构模型，其中，桥梁拱肋的约束混凝土采用具有Han模型本构[8]的Concrete02混凝土材料来模拟，桥墩的约束及非约束区混凝土均采用具有Kent-Scott-Park本构模型[9]的Concrete02混凝土材料进行模拟. 拱肋和横撑的钢管、吊杆以及桥墩中的纵向主筋均采用具有Giuffre-Menegotto-Pinto 本构关系模型[10]的Steel02材料来模拟.

全桥空间非线性有限元模型如图2所示. 对桥梁施加阻尼比为2%的瑞利阻尼，并计入P-Δ（竖向荷载-水平位移）效应的影响，经过特征值分析，桥梁的前5阶自振周期如表1所示.

图2 桥梁有限元模型Fig. 2 Finite element model

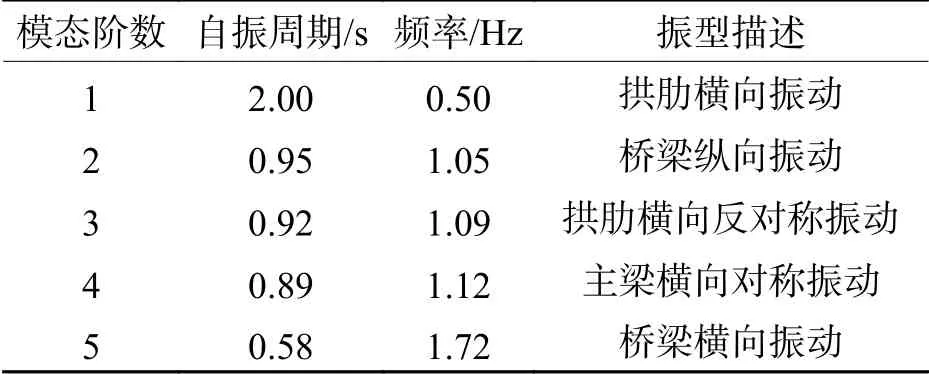
表1 桥梁自振特性Tab. 1 Vibration characteristics of bridge

2 多点多维地震动合成

地震动的空间效应包括行波效应、失相干效应以及场地效应. 因为地震台记录的天然地震动具有不同的位置差异，与实际大跨度结构的实际位置有所不同，在工程实际中，常用的做法是人工合成与特定反应谱相结合来生成空间变异性地震动. 以往的学者提出了大量的人工合成随机地震动的方法[11-12].本文选取Bi等[13]提出的方法进行空间变异性地震动合成，并且按照《公路桥梁抗震设计细则》中的规定考虑不同场地条件的影响，将场地类型划分为3个级别，分别是软土、中软土和硬土（分别以S、M、F表示）. 假定1# 与4# 墩底的场地条件为坚硬类型，2# 与3# 墩处场地类型一致. 不同点失相干公式采用Hao等[14]对SMART-1地震动序列分析推导得到，如式（1）.

式中： β为常数；djn为点j、n间的距离；vapp为地震波传播速度； γjn(iω)为两支撑点j、n间的相干损失；α(ω) 如式（2），ω为圆频率.

式中：a、b、c均为常数.

为对比不同地震波传播速度的影响，本文假定vapp分别为250、500 m/s和1 000 m/s. 为考察失相干程度的影响，考虑了高、中等、弱相干性地震动，其相应参数取值详见文献[15]. 地震波的采样频率和上截断频率分别为100 Hz和25 Hz，地震波持时为20.48 s.

本文共设置了10种空间变异性工况，并列于表2. 表中：场地类型为4个支撑点的场地类型. 在工况1中，地震动传播速度假定为无限大，并且无失相干损失，即表示一致地震动激励；在工况2中，仅在桥梁顺桥向设置地震波的传播速度为500 m/s，无相干损失，即仅具有行波效应的空间变异性地震动；同理，工况3仅有中等程度的相干损失，不考虑行波效应；后面7种工况为同时考虑失相干效应、场地效应以及行波效应的分析工况.

表2 空间变异性地震动工况Tab. 2 Spatial ground motion cases

为得到更为准确的结构响应，每个工况随机生成了20组地震波时程，计算时地震波纵向与横向的地震加速度（PGA）取为一致，竖向地震动的强度假定为水平分量的2/3. 在实际的计算中，为获得较为明显的结构响应，将水平地震动的PGA调幅至0.5g，竖向地震动按同样比例调幅. 以工况4的第1组地震波为例，图3表示的是各个支撑点处的加速度和位移时程曲线. 图4对比了人工生成的非一致地震动的反应谱与目标反应谱（坚硬场地），可以看出吻合程度较高. 图5给出了人工模拟地震动与经验函数得到的失相干损失对比情况.图中，|γ12|、|γ13|、|γ14|为1号支撑点与其余3个支撑点间的失相干损失. 同样吻合情况良好，这足以说明按照上述方法合成的多点多维地震动样本满足要求，可以进行下一步计算分析.

图3 各支撑点处非一致地震动加速度与位移时程曲线(工况4)Fig. 3 Generated spatially varying ground motions on different sites (case 4)

图4 人工生成地震波反应谱与设计反应谱对比（坚硬场地）Fig. 4 Comparison of the simulated acceleration and the code response spectrum (firm)

图5 人工生成地震波失相干损失与经验函数对比Fig. 5 Comparison of the coherency loss between simulated ground motions and the empirical function

3 桥梁多点多维地震反应结果分析

3.1 综合对比

为避免由于地震波的随机性所引起结果偏颇，分别计算出每种工况下的20组人工地震动作用时桥梁结构响应的平均值. 绘出前4种工况下桥梁拱肋内力及位移响应峰值的包络图，如图6所示，并统计出2# 和3# 主墩的内力及位移峰值的平均值如表3所示，其中剪力为纵桥向，拱肋和墩底的弯矩均为面内弯矩，表格中的位移则代表墩顶的纵向位移.由图3可知：地震动的空间变异性效应对拱肋的地震响应影响显著，一致地震动作用下桥梁上部结构的地震响应普遍偏高. 同综合考虑行波效应、失相干效应及场地效应的非一致地震动相比，一致地震动激励下拱肋的轴力峰值增大约10%，左拱脚处的面内弯矩增大约30%，仅考虑行波效应或者仅考虑失相干效应时拱肋的地震响应结果与一致激励的结果相近. 类似地，从表3可以看出：与其他几种形式的非一致地震激励相比，一致地震激励会明显加剧连续梁拱桥主墩的内力及位移响应. 另外，当仅考虑行波效应时，会严重低估桥梁下部结构的内力及位移响应. 综合而言，仅考虑一致地震动激励可能会过高估计桥梁结构的地震响应，仅考虑行波效应可能会过低估计桥墩的内力及位移响应. 因此，在大跨度连续梁拱桥的地震反应分析时，宜综合考虑地震动的空间变异性效应.

3.2 失相干效应的影响

为研究失相干效应对桥梁结构地震响应的影响，对比了工况10、4和9（分别代表高、中等和低相干）下桥梁结构的地震响应. 绘出桥梁结构拱肋的内力及位移的峰值响应包络图如图7所示，统计出2#和3# 主墩的内力及位移峰值的平均值如表4所示.从图中可以看出：地震动的失相干程度对连续梁拱桥上部结构的地震响应影响显著，随着失相干程度的增大，拱肋轴力、拱脚处的弯矩响应不断增大，而拱肋的位移响应恰恰相反，其与地震动的失相干程度呈正相关. 对下部结构而言，2# 墩墩底的内力和3# 墩的位移均在失相干程度较低时取得极大值，而3# 墩墩底的剪力与2# 墩的位移均在失相干程度较高时取得极大值，这可能与人工生成地震波的失相干损失曲线具有较大的波动性有关. 总体而言，在考虑地震动的空间效应时，应注意恰当衡量地震波的失相干损失程度.

图6 多点多维地震动下桥梁拱肋峰值响应包络图Fig. 6 Peak seismic responses envelope of arch rib under multi-point and multi-dimensional ground motions

表3 多点多维地震动下桥墩峰值响应Tab. 3 Peak seismic responses of pier under multi-point and multi-dimensional ground motions

图7 不同失相干程度时拱肋峰值响应包络图Fig. 7 Peak seismic responses envelope of arch rib with different coherency loss

表4 不同失相干程度时桥墩峰值响应Tab. 4 Peak seismic responses of pier with different coherency loss

3.3 场地效应的影响

同样地，为研究不同场地类型对大跨度连续梁拱桥地震响应的影响，对比了工况4、5和6（分别代表1#和4# 墩底为坚硬土质的情况下，中间2# 与3# 墩底场地类型分别为坚硬、中等与松软）下桥梁拱肋及桥墩的地震响应情况. 作出3种不同场地类型下桥梁结构拱肋及桥墩的内力峰值响应包络图，如图8所示，统计出桥梁2# 和3# 主墩的内力及位移峰值响应的平均值如表5所示. 由图表可见，场地效应对大跨度连续梁拱桥地震响应的影响规律极其清晰，随着场地条件逐渐变松软，桥梁拱肋和桥墩的内力及位移响应均逐步增大，并且增幅较大. 这是由于场地越软，场地的卓越频率越接近于结构的基频，容易激起结构共振. 由此，在桥梁结构的抗震分析中，应准确判定支撑处的场地条件.

图8 不同场地类型时拱肋峰值响应包络图Fig. 8 Peak seismic responses envelope of arch rib with different soil conditions

表5 不同场地类型时桥墩峰值响应Tab. 5 Peak seismic responses of pier with different soil conditions

3.4 行波波速的影响

类似地，图9给出了不同地震波传播速度下（1000、500 m/s与250 m/s）桥梁结构拱肋的内力及位移峰值响应包络图. 表6给出了不同行波波速下桥梁主墩墩底的内力及墩顶的位移峰值响应情况. 可以看出，行波效应对桥梁结构地震响应的影响也不容忽视. 随着地震波传播速度的减弱，拱肋的轴力响应呈先减后增的趋势，低速（250 m/s）时的响应最为剧烈，拱肋的面内弯矩也是在低速时响应较为剧烈，拱肋的纵向及横向位移与行波波速呈正相关关系. 对下部结构而言，地震动传播速度为1000 m/s时，2# 和3# 墩底的纵向剪力及面内弯矩大多取得极大值，墩顶的位移基本不受行波波速的影响. 综合来看，行波效应对桥梁结构的地震反应没有较为明确的规律，拱肋及桥墩的动力响应可能在波速较低或较高时取得极值，在考虑地震波的行波效应时，应尽可能多选几个波速，取最不利结果.

图9 不同行波波速时拱肋峰值响应包络图Fig. 9 Peak seismic responses envelope of bridge with different apparent wave velocities

表6 不同行波波速时桥墩峰值响应Tab. 6 Peak seismic responses of pier with different apparent wave velocities

4 结 论

本文对主跨为139 m的连续梁拱桥进行了多点多维地震激励下的动力响应分析，探究不同非一致地震参数对桥梁结构响应的影响规律，得到如下结论：

1） 地震动的空间效应会对连续梁拱桥的动力响应产生较为明显的影响，仅考虑一致地震动激励可能会高估该类桥梁的地震反应，采用一致激励的计算结果偏于安全、保守；

2） 地震动的失相干效应会显著影响连续梁拱桥的地震响应，随着失相干程度的增大，拱肋轴力、拱脚的弯矩响应不断增大，拱肋的位移响应不断减小，而下部结构的响应可能增大，也可能减小；

3） 桥梁支撑点的场地效应对桥梁结构地震响应影响最为突出，随着支撑点处的场地越来越松软，桥梁各个部位的内力及位移响应均大幅增加；

4） 地震动的行波效应对桥梁的地震响应没有较为明确的影响规律，但不可忽视其作用，地震波传播速度较低或较高时，连续梁拱桥关键部位的地震响应可能取得极大值，但仅考虑行波效应时会严重低估下部结构的地震响应.