小游戏引出大道理

文 陆余庆

图形的平移、旋转和翻折是几何中最基本的三种变换，它们都不会改变图形的形状和大小，自然界中许多图案的设计灵感都是来源于此。其中，由旋转这一变换提出了中心对称图形的概念，进而介绍了一种特殊的中心对称图形，即平行四边形。其实，这一内容的背后可有着许多有趣的数学故事和思想方法，同学们，你们知道多少呢？

先看这样一则小游戏：甲乙两人轮流往一张圆桌面上放一枚五分硬币且不能重叠，谁放完一枚以后而使得对方无法往桌面上放硬币时，谁就是胜利者。如果甲先放，有没有稳操胜券的策略？请大家先独立思考，试着找到必胜的策略。事实上，如果甲先在圆心处放上一枚硬币（如图1），占据主要地位，那么之后无论乙把硬币放于何处，甲只要在乙所放位置关于中心点对称的位置上放上另一枚硬币就可以了（如图2）。我们知道，只要乙有可放硬币的地方，那么甲就总是可以找到与之对称的另一位置，如此，甲必胜。其实，这一游戏还可推广到一般的情形，可将圆桌换成平行四边形、正六边形或其他任意的中心对称图形，则甲仍有先手优势。制胜策略正是借助中心对称图形的特征，将实际问题抽象成数学问题，转化为在中心对称图形中依次取点的问题。从特殊到一般的思想方法在解决问题的过程中是非常常见的，除此之外，通过逆向思维，再回到最特殊的情形，往往也能更快得出答案。例如，上述游戏中，不妨将圆桌取为最极端的情况——一个点，显然谁先放硬币谁就取胜，先手优势不言自明。

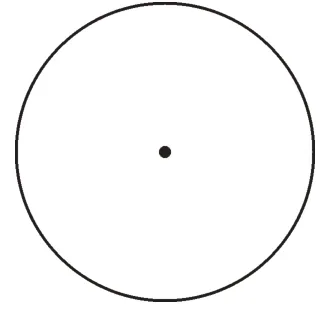
图1

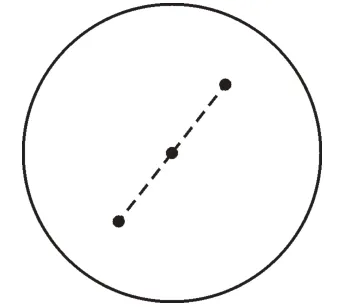
图2

此外，中心对称图形还在分形这一数学理论中占有一席之地哦！分形通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”，即具有自相似的性质。分形理论是芒德勃罗提出来的，分形原意具有不规则、支离破碎等意义。自然界中存在着许多分形现象，如花椰菜、冻豆腐、磁铁等，而人造的分形现象若和中心对称图形结合起来，则会碰撞出另一种火花。比如，科赫雪花曲线就是中心对称图形（如图3），局部放大后的图形仍和本体的形状是相似的。它是以等边三角形三边生成的科赫曲线组成的。它的面积是，其中s是原来三角形的边长。这一几何图形的周长无限大，但面积却是有限的。想不到外形独特美丽的它还有如此有趣的结论。同学们，你能尝试着设计出分形现象中的中心对称图形吗？

图3