基于云模型的西藏高原灌区参考作物蒸散量时间变化特征与影响因子研究

刘静霞，蒙强，曹志翔，李玉庆，张文贤

（西藏农牧学院水利土木工程学院，西藏林芝 860000）

0 引言

【研究意义】参考作物蒸散量（ET0）是估算作物需水、制定灌溉制度、建立生态模型[1]及评价区域水资源利用情况的基础参数，开展ET0的理论研究对优化农田水分管理与农业种植模式、提高农业灌溉智能化等生产实际问题具有重要的指导意义[2]。但ET0的时空变异性较大，且时间上的随机性、模糊性和空间上的相似性、特殊性共存。同时，影响ET0的因子较多，其中ET0对气象因子的变化比较敏感，但气象因子时空变异性大且各因子间的组合复杂多样[3]，这给学者从理论上进一步揭示ET0的时空变异机理及其成因带来困难，同时也影响不同时空尺度下ET0的精确测算。

【研究进展】目前，针对ET0的研究主要采用的方法包括趋势分析[4]、相关分析[5]、地统计学法[6]、经验正交函数[7]等，这些方法虽能定量表达ET0的时空分布规律，却难以定量描述ET0时空分布的均匀性、稳定性等不确定性特征。然而，定量化表达ET0变化的不确定性不仅是揭示ET0时空变异规律及其变化成因的有效途径[8]，也是进一步扩展ET0理论研究尺度及提高ET0预测精度的基础。当前，由李德毅院士提出的云模型[9]是实现定性概念与定量表示的相互转化的模型，且该模型能将自然界中的随机性、模糊性定量表示。目前，已有学者将云模型的应用从降水量预测[10]、空气质量评价[11]、水资源承载力分析[12]等领域逐步扩展到ET0的相关研究中，已直观地将ET0时空变化的随机性、模糊性、均匀性等不确定性特征通过云模型的数字语言进行了定量表达。例如，赵璐等[8]首次基于云模型研究了四川省ET0的时空分布，发现空间尺度上ET0分布不均匀且不均匀性在时间尺度上存在波动；殷长琛等[13]、康燕霞等[14-15]采用云模型分析了甘肃省ET0的时空变化，认为在时间尺度上甘肃省ET0的分布相对均匀、稳定，而空间尺度上的均匀性和稳定性随研究区域的变化而变化；此外，许健等[16]运用云模型研究了我国ET0的时空分异特征，发现研究的时间尺度越长，ET0时间分布的不均匀性及不均匀性的稳定性越大。

【切入点】然而，西藏地区有关ET0的理论研究起步较晚，前人虽采用趋势分析[4]、相关性分析[5]、贡献率分析[14]等方法对ET0的时空分布变化及其成因进行了定量描述，但有关ET0时空分布的均匀性及稳定性的描述以及云模型在西藏地区ET0的变化中的应用鲜见报道。【拟解决的关键问题】综上，鉴于云模型在我国其他区域ET0研究中的成功应用，本研究拟选取西藏高原典型灌区为研究区域，利用灌区 1991—2016 年逐日气象资料通过 FAO56 Penman-Monteith 方法计算ET0，并采用云模型对ET0的时间变化特征及其影响因子进行研究，以期为西藏高原灌区建立成熟的灌溉制度与发展智慧型节水技术提供理论参考。

1 数据与方法

1.1 研究区概况及数据处理

西藏的灌区主要分布在日喀则、山南地区。其中，满拉、墨达、江北灌区是分别位于日喀则、拉萨、山南地区灌溉面积超过2×104hm2的大型高原灌区。本研究综合分析了灌区面积、行政区划、农业种植等条件后，选取满拉、墨达、江北3 个灌区作为典型研究区域，灌区研究站点的基本情况见表1。

表1 研究站点的基本情况[17-19]Table1Characteristics of the studied site[17-19]

满拉、墨达、江北灌区附近的气象站点分别为江孜、墨竹工卡和贡嘎，各站点1991—2016 年的逐日气象观测资料（日最高气温、日最低气温、平均气温、相对湿度、降水、日照时间等）均来源于中国气象数据中心。在数据处理方面，针对个别气象数据日缺失值及异常值采用该值的前后日均值代替；对于长期月缺失值和异常值采用该站点其他年份对应月的均值代替[12]。云模型采用MATLAB 软件编程处理；ET0及气象因子的倾向率采用线性相关趋势方程斜率的10 倍描述。

1.2 研究方法

1.2.1 参考作物蒸散量（ET0）的计算

采用FAO 推荐的FAO 56Penman-Monteith 模型计算ET0，其计算式[20]为：

式中：ET0为参考作物蒸散量（mm/d）；∆为饱和水汽压—温度曲线斜率（kPa/℃）；Rn为太阳净辐射（MJ/（m2·d））；G 为土壤热通量（MJ/（m2·d））；γ为湿度计常数（kPa/℃）；T 为2 m 高度处日平均气温（℃）；es为温度为T 时的实际水汽压（kPa）；ea为温度为T 时的饱和水汽压（kPa）；U2为2m 高处的日平均风速（m/s）。以下与此公式中的参数、符号相同者意义均相同。

1.2.2 云模型

云模型是由李德毅院士1995 年提出的处理定性概念与定量表示的不确定性转换模型，该模型反映了自然界中的模糊性、随机性及二者间的关联性[21]。而云模型数字特征期望Ex、熵En、超熵He（图1）是语言值数学性质的表达。其中，Ex 表示ET0在论域空间中分布的期望[13]；熵En 表示数域空间中能被定性概念所接受的ET0的范围，同时也表示ET0的大小相对于其均值的离散程度；超熵He 取决于En 的随机性和模糊性，能反应“云滴”分布的凝聚性，即云的“厚度”。He 越大，表示云滴的离散度越大，即云滴凝聚的“厚度”也越大，云分布则越不稳定[22-23]。此外，根据正态分布的特征，数域中表征定性概念的有贡献的云滴主要分布区间为[Ex-3En，Ex+3En]，因此忽略上述数域区间之外云滴的贡献，即为正向正态云的“3En”规则[22]。

1）正向云算法

正向云发生器描述了定性概念到定量表示的不确定性转换，按照云模型的数字特征Ex、En、He 产生云滴，当云滴凝聚到一定量级后汇聚为云。具体计算步骤[21-23]如下：

①以En 为期望，He2为方差生成一个正态随机数Eni'，Eni'=NORM (En，He2)；

②以Ex 为期望，Eni'为标准差生成一个正态随机数Xi，Xi=NORM (Ex，)；

③计算隶属度ui，计算式为：

④ui与xi共同确定出隶属于数域中的云滴；

⑤重复上述步骤，直至产生n 个云滴为止。

2）逆向云算法

逆向云发生器是实现将定量数据转换为Ex、En、He 所表示的定性概念的过程，具体计算步骤[21-23]如下：

①依次计算ET0的样本均值X、一阶样本绝对中心矩a 和方差S2，其中期望Ex=X，各项计算式分别为：

②由一阶样本绝对中心矩a 计算熵En，计算式为：

③由样本方差S2和熵En 计算超熵He，计算式为：

1.2.3 Mann-Kendall(M-K)检验

世界气象组织推荐的Mann-Kendall 法是一种非参数检验方法[24]，该方法不受样本（x1，x2，…，xn）分布情况及少数异常值的影响，具有较强的适用性。当该检验方法的统计指标Z 为正值时，表明样本的时间变化呈增长态势，其中若Z＞1.64，则说明增长趋势显著（置信度α=0.05）；当Z 为负值时，表明样本的时间变化呈降低趋势，其中若Z＜-1.64，则说明降低趋势显著（α=0.05）；当-1.64≤Z≤1.64 时，表明样本的时间变化不显著（α=0.05）[25-26]。

1.2.4 通径分析

通径分析（Path analysis）是研究变量相互间及自变量对因变量作用效果的统计方法。与一般相关分析相比，通径分析能进一步的量化变量间的相互作用效应[27]。因此，运用该分析方法不但能衡量自变量对因变量的直接及间接作用效应，而且也能找出由自变量间的强相关性而引起多重共线影响的自变量[27-28]。在具体分析过程中，运用SPSS 中的多元回归法计算相关系数，并将其分解为不同作用路径下的直接通径系数、间接通径系数及总通径系数，然后据此评价指标间的影响效应。

2 结果与分析

2.1 ET0 年际变化分析

图2 为西藏3 个灌区ET0年际变化情况，由图2可知，江北、满拉、墨达灌区的ET0在年际间呈持续性上下波动，年ET0分别介于965.12～1100.71、923.46～1074.83、926.42～1088.45mm 之间。线性趋势变化显示，江北灌区年ET0（Shapiro-Wilk 检验值W=0.973）以27.97 mm/(10a)的倾向率递减，其中M-K 统计指标Z=-3.75＜-1.64，表明降低趋势显著（α=0.05）。满拉灌区年ET0（W=0.951）以9.99 mm/(10a)的倾向率递增，其中统计指标Z=1.32，表明递增趋势不明显；墨达灌区年ET0（W=0.974）以6.41 mm/(10a)的倾向率递减，其中统计指标Z=-0.35，表明递减趋势不明显。5a 滑动平均曲线变化表明，满拉、墨达灌区年ET0在1991—2005 年浮动频率大，均呈“先降低后升高”的变化趋势，但2005 年之后墨达灌区年ET0的浮动变化较平稳。整体上，江北灌区1991—2016 年间的ET0浮动变化较平稳。

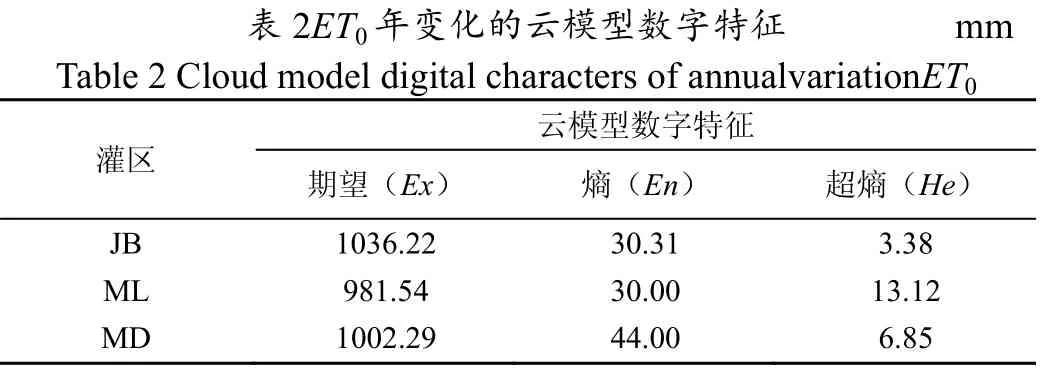
Table2Cloud表2ET0 年变化model digital的云模型数字characters of a云模型数字特特征nnualvariation E征mm T0灌区期望（Ex）熵（En）超熵（He）JB 1036.22 30.31 3.38 ML MD 981.54 1002.29 30.00 44.00 13.1 6.85 2

2.2 ET0 季节及月变化分析

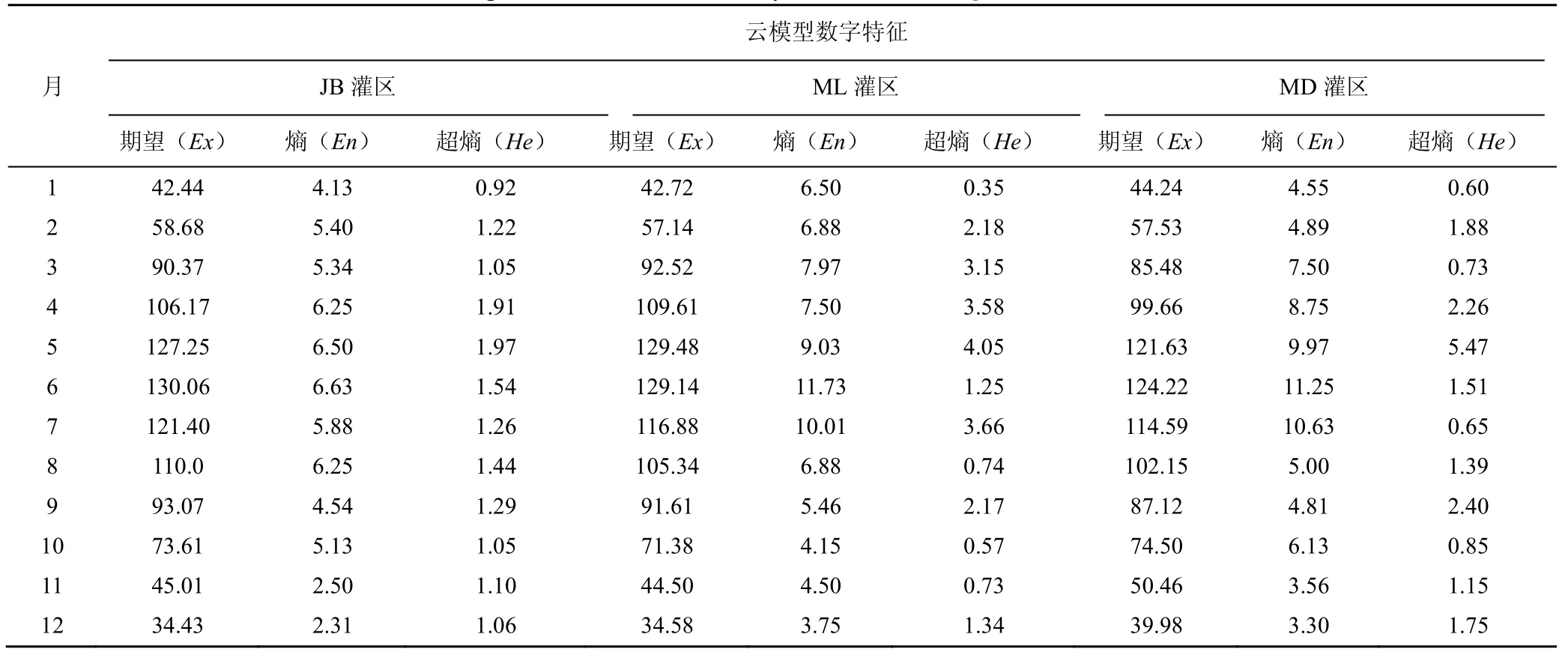
表4 西藏3 个灌区ET0 月变化的云模型数字特征Table 4Cloud model digital characters of monthly ET0 in three irrigation districts in Tibet mm

2.3 气象因子变化分析

表5 为西藏3 个灌区气象因子的变化及云模型数字特征。由表5 可知，1991—2016 年江北、满拉、墨达3 个灌区多年平均气温分别为8.95、5.50 和6.63℃。其中，满拉、墨达灌区的平均气温在年际间分别以0.40、0.70 ℃/(10a)速率呈显著增加趋势；江北灌区的平均气温在年际间增长趋势不显著，增长速率为0.23℃/(10a)。江北、满拉灌区平均温度的En 小于墨达灌区，表明江北、满拉灌区平均温度分布的均匀性高于墨达灌区。总体上，3 个灌区平均温度的He较小，介于0.11～0.12 之间，且云图显示（图6）云滴的凝聚性均高、云“厚度”较薄，表明3 个灌区平均温度分布的稳定性整体较好。

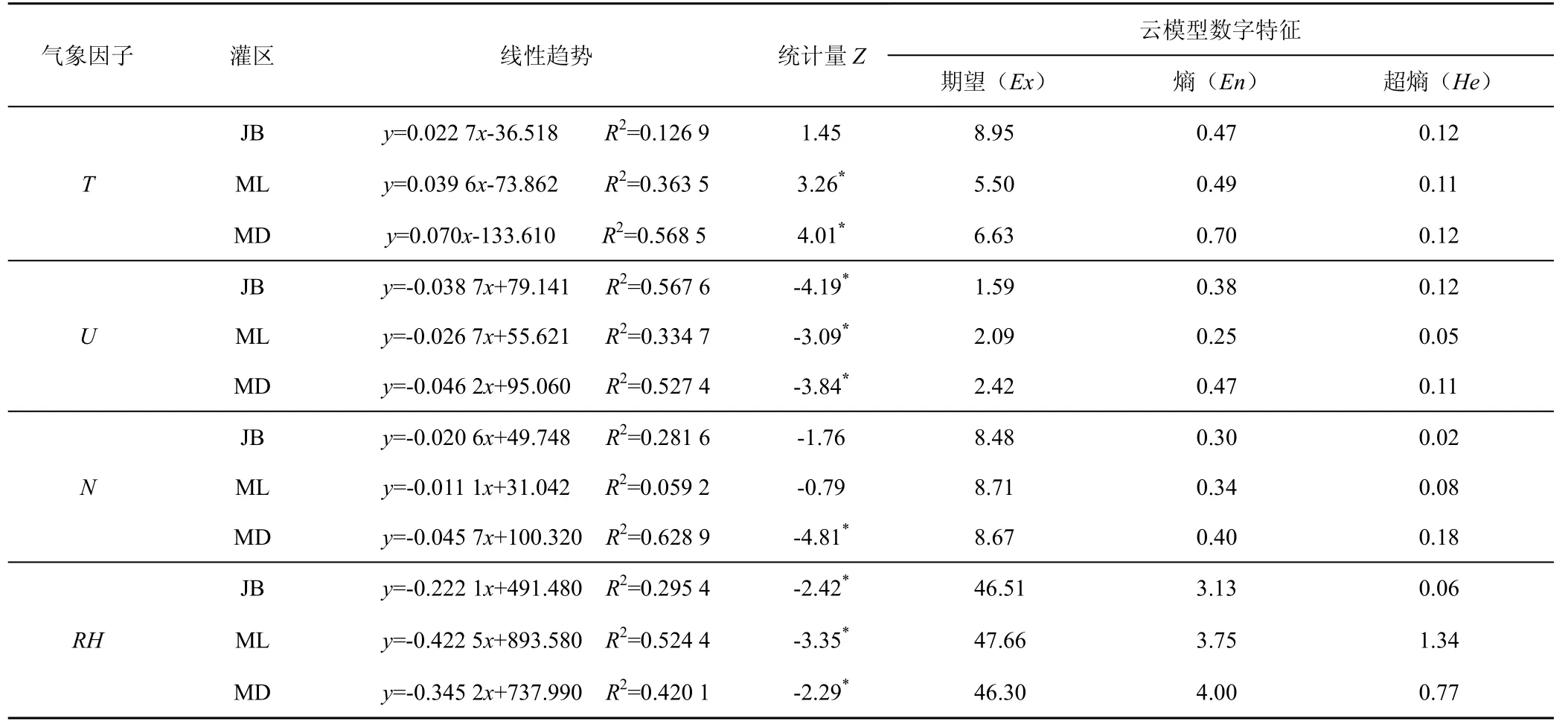
表5 西藏3 个灌区气象因子的变化及云模型数字特征Table 5 Annual change of meteorological factors and cloud model digital characters in three irrigation districts in Tibet

1991—2016 年江北、满拉、墨达灌区的多年平均风速分别为1.59、2.09 m/s 和2.42m/s，且均在年际间的递减趋势显著，其递减速率分别为0.39、0.27 和0.46m/(10a)。云数字特征结果显示，江北、满拉、墨达灌区的En 分别为0.38、0.25 和0.47，表明满拉灌区平均风速分布的均匀性最高，江北灌区次之，墨达灌区最差。满拉灌区的He 最小，为0.05，同时云滴的凝聚性最高且云“厚度”最薄，表明26a 来满拉灌区平均风速分布的稳定性最高，其他2 个灌区的稳定性较差。

1991—2016 年江北、满拉灌区的多年平均日照时间分别为8.48、8.71h，且在年际间的递减趋势不显著，递减速率分别为0.21、0.11h/(10a)。墨达灌区的多年平均日照时间为 8.67 h，且在年际间以0.46h/(10a)的速率显著增加。3 个灌区日照时间的En相对较小，介于0.30～0.40 之间，表明日照时间分布的均匀性总体较高。江北灌区的He 最小，云滴凝聚性最高且云“厚度”最薄，表明江北灌区日照时间分布的稳定性最高，满拉灌区次之，墨达灌区最差。

1991—2016 年江北、满拉、墨达灌区的平均相对湿度分别为46.51%、47.66%和46.30%，且在年际间的递减趋势显著，递减速率分别为2.22%/(10a)、4.23%/(10a)和3.45%/(10a)。3 个灌区平均相对湿度的En 相对其他气象因子较大，介于3.13～4.00 之间，表明平均相对湿度分布的均匀性较低。江北灌区的He最小、云滴凝聚性最高且云“厚度”最薄，表明其日照时间分布的稳定性高。

综上所述，江北、满拉、墨达3 个灌区中平均温度均呈递增趋势，平均风速、日照时间、平均相对湿度均呈递减趋势。平均相对湿度、日照时间分布的均匀性及稳定性以江北灌区的最高；平均风速分布的均匀性及稳定性以满拉灌区的最高；3 个灌区平均温度分布的均匀性及稳定性整体较高。

2.4 ET0 与气象因子的通径分析

表6 为不同气象因子与江北、满拉、墨达灌区ET0的通径分析结果。由表6 可知，平均气温（T）、平均风速（U）、日照时间（N）和平均相对湿度（RH）均对ET0产生影响，且各气象因子的直接、间接作用效果均存在差异。总体上，各气象因子对江北、满拉、墨达灌区ET0的直接作用程度分别为U＞N＞RH＞T、RH＞N＞U＞T、RH＞N＞U＞T；其中RH 对3 个灌区的ET0均产生负向直接作用，其余气象因子为正向直接作用。RH 对满拉、墨达灌区ET0直接作用最显著，直接作用系数分别为-0.531 和-0.543；U 对江北灌区ET0直接作用最显著，直接作用系数为0.914。

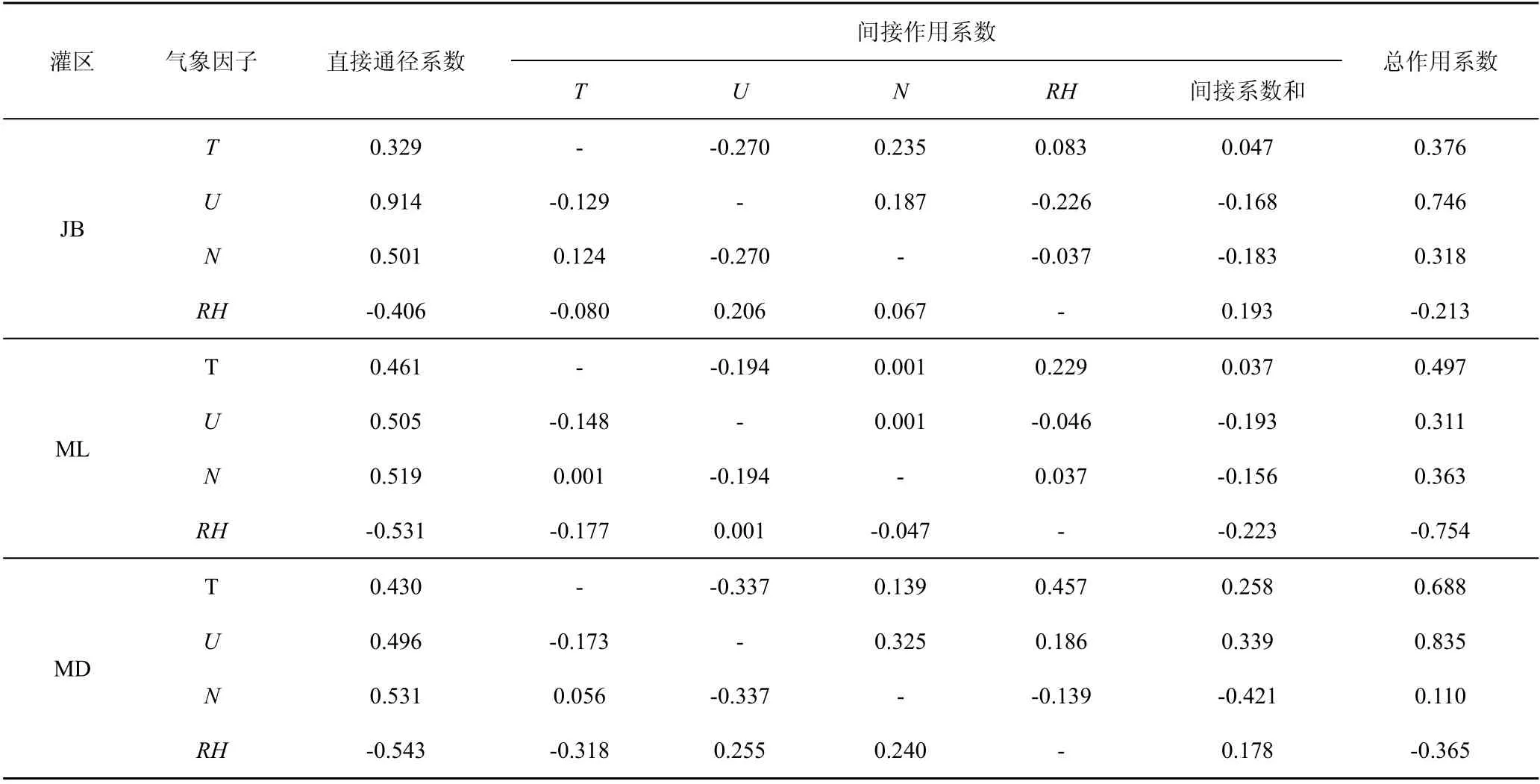
表6 气象因子与年ET0 的通径分析Table6 Path analysis between meteorological factors and the annual ET0

分析各气象因子对ET0的间接作用可知，RH 对江北、满拉灌区ET0的间接作用最为显著，间接作用系数分别为0.193、-0.223；N 对墨达灌区ET0的间接作用最为显著，作用系数为-0.421。由气象因子间的相互作用可知，T 与RH 间的相互作用最强，T 与U的相互作用次之。综上可知，各气象因子间存在相互制约和相互影响的关系，且ET0的变化受各气象因子的综合影响。

3 讨论

近几十年来，随着全球气候不断变化，不同尺度下ET0时空变异规律及其成因的研究引起了学者的广泛关注[20]。目前，有关西藏地区ET0研究报道及积累的研究成果较少且前人主要采用趋势分析[4]、相关分析[5]、地统计学法[6]等方法仅定量分析了ET0的时空分布特征，而对西藏ET0时空分布的随机性、稳定性的研究从未见报道。因此，本研究借助李德毅院士提出的定性概念与定量表示能相互转化的云模型[9]，将江北、满拉、墨达灌区ET0时间尺度上分布的随机性与稳定性通过云模型的数字语言（期望Ex、熵En、超熵He）结合云分布图的形式直观地表达出来，以期为西藏ET0时空变化规律的研究提供新的思路。

趋势分析发现，江北、墨达灌区多年ET0分别以27.97、6.41 mm/(10a)的倾向率递减，满拉灌区多年ET0以9.99 mm/(10a)的倾向率递增，但变化趋势均不显著，这与杨永红等[29]、张娜等[19]研究发现西藏整体上ET0呈降低趋势的研究结论不一致。其原因可能与杨永红等[29]、张娜等[19]的研究结论是基于西藏整体气候区，而本研究结论仅针对西藏不同气候区中的半干旱气候区有关。同时也间接表明同一气候类型下西藏不同区域的多年ET0变化趋势存在区域性差异。此外，趋势分析结果也显示，3 个灌区的平均温度、平均风速、日照时间、平均相对湿度呈递减趋势，而平均温度呈递增趋势。对比同一灌区ET0及其影响因子的变化趋势发现，江北、墨达灌区多年ET0呈降低趋势，而平均温度却呈上升趋势，显然温度上升并未引起ET0增加，即存在“蒸发悖论”现象[30]，这与武剑飞等[31]、陈超[32]、冯禹[33]等的研究结果一致。同时也间接说明平均温度并不是影响江北、墨达灌区ET0变化的主要因子，这与本研究通径分析结果相互印证，即平均风速、平均相对湿度分别为影响江北灌区ET0变化直接和间接作用最显著的气象因子；平均相对湿度为影响满拉灌区ET0变化直接和间接作用最显著的气象因子；平均相对湿度、日照时间分别为影响墨达灌区ET0变化直接和间接作用最显著的气象因子。这与张娜等[19]基于偏相关分析得出的平均气温对西藏ET0的影响程度最大的结论不一致，可能原因是张娜等[19]忽略了气象因子间的强相关性而引起多重共线影响外，也与不同区域的地理、气候环境下影响ET0变化的气象因子不同有关。

由各灌区气象因子、年ET0变化趋势及通径分析结果可知，平均风速、平均相对湿度是影响3 个灌区年ET0变化的主要因子，其次为平均温度。进一步对比各影响因子分布的均匀性及稳定性发现，同一灌区中影响ET0变化最显著的气象因子在时间尺度上分布的均匀性及稳定性较差，然而该结论是否具有较广的普适性，还需进一步在其他区域进行验证。

4 结论

1）江北、墨达灌区多年ET0分别以27.97、14.84mm/(10a)的倾向率递减，满拉灌区年ET0以9.99mm/(10a)的倾向率递增，但变化趋势均不显著。江北灌区年ET0分布的均匀性及稳定性最高；墨达灌区的均匀性及稳定性最差。季节尺度上，3 个灌区的ET0均呈夏季＞春季＞秋季＞冬季的分布特点，且冬春季ET0分布的均匀性及稳定性最高，夏秋季的均匀性及稳定性最差。月尺度上，ET0呈中间高、两端低的单峰形分布。

2）江北、满拉、墨达3 个灌区中平均温度呈递增趋势；平均风速、日照时间、平均相对湿度呈递减趋势。平均相对湿度、日照时间分布的均匀性及稳定性以江北灌区的最高；平均风速分布的均匀性及稳定性以满拉灌区最高。

3）平均风速、平均相对湿度是影响江北、满拉、墨达灌区年ET0变化的主要气象因子。