基于机器学习方法的土壤转换函数模型比较

左炳昕，查元源

（武汉大学水资源与水电工程科学国家重点实验室，武汉430072）

0 引言

【研究意义】农业水肥管理、作物模型估产、陆面模型建模、生态环境治理与修复等，都离不开土壤水分状态及运动过程的准确描述与预测[1-2]。土壤水分特征曲线和水力传导度（又称为渗透系数）曲线，作为描述土壤水力性质最基本的2 条曲线，在非饱和土壤的物理、化学、生物过程的定量化描述中起着基础性的作用[3]。某含水率下的相对水力传导度为该含水率下的（绝对）水力传导度与饱和水力传导度的比。研究表明，相对水力传导度是可以由土壤水分特征曲线推导得到，所以，水力传导度曲线可以由土壤水分特征曲线与饱和水力传导度确定。因此，土壤水力参数可以认为由土壤水分特征曲线参数与饱和水力传导度组成。土壤水力参数的直接测量要么昂贵费时费力，要么适用性有限。间接法通常包括土壤转换函数（PedoTransfer Functions，PTF）、分形方法、土壤形态学方法、数值反演方法、经验公式法等[4]。其中，土壤转换函数模型只需要输入土壤粒径信息、体积质量、有机质量等简单易得的物理量，就可以估算土壤水力参数，简单方便，大大降低了土壤水力参数获取的时间成本和操作难度，因而得到了广泛使用。

【研究进展】在土壤水力参数简便获取方法的探索中，20 世纪初期，Briggs 等[5]研究了易获得的数据和待预测数据之间的关系。20 世纪80 年代后，随着新的土壤水分特征曲线模型的提出，土壤参数获取方法的研究也更为广泛。Bouma 等[6]首次提出了土壤转换函数的概念，Bouma[7]与Hamblin[8]将土壤转换函数表述为土壤较易测量的数据与难以测量的数据之间的函数关系。

建立土壤转换函数的方法主要包括线性回归、非线性回归、人工神经网络等。这些方法中，以神经网络方法应用最广，很大程度是神经网络不需要预先设定函数的形式（如指数形式等），预测精度比较高等原因。近年来也有采用新的方法建立土壤转换函数，如最近邻居法、支持向量机、多尺度贝叶斯神经网络等。

Nemes 等[9]使用分层的预测变量集，基于最近邻居法，预测了330cm 与15000cm 负压下的含水率。Lamorski 等[10]基于支持向量机（机器学习领域替代性的数据驱动的方法），提高了模型的效率。Zhang 等[11]使用加权改进的神经网络算法建立了适用于全球的土壤转换函数。关于土壤转换函数，国内也做了很多研究[12-15]。

【切入点】虽然土壤转换函数的研究较多，但不同研究在建立土壤转换函数时所使用的数据集不同。由于缺乏物理基础，以及在建模时使用的数据有限，土壤转换函数在应用时应注意其适用性。例如，Gijsman 等[16]比较了8 种土壤转换函数，由于构建模型的数据来自不同地区，不同土壤转换函数模型的预测效果显示出了明显的差异。因此，使用同一数据集定量比较建立土壤转换函数的方法，对于建立合理高效的土壤转换函数模型，具有重要意义。

【拟解决的关键问题】本研究采用UNSODA 数据库中土壤样品的基本性质数据（包括土壤砂粒、粉粒、黏粒百分比、土壤体积质量）作为土壤转换函数的输入项；利用van Genuchten（简称VG）模型[17]拟合土壤含水率-负压数据（土壤基本性质相对应的数据）得到VG 参数作为模型的输出项，采用多种机器学习方法，建立土壤样品的基本性质数据与VG 模型参数之间的关系，对比不同机器学习方法的预测效果，并讨论其计算效率。

1 材料与方法

1.1 试验数据

本文采用全球土壤非饱和水力性质数据库UNSODA（UNsaturatedSOilDAtabase）。该数据库记录了野外场地条件和实验室条件下的土壤样本的含水率、负压、非饱和水力传导度、扩散度等关系，以及相对应的土壤理化性质指标，如土壤粒径分布、土壤颗粒密度、体积质量、有机质量、pH 值、阳离子交换量等。由于其样品空间分布范围广、样品数量多、土壤质地类型丰富等特点，常用于分析土壤物理基本性质[18]。

本文整理了UNSODA 数据库中实验室条件下测得的含有8 个以上含水率-负压数据且包含一个330 cm 以上负压值的土壤样品（以保证土壤样本不被过度拟合，且在田间持水率以下有一个代表性的数据点）；在此基础上筛选出其中可以提取到质地信息和土壤体积质量信息的土壤样本，并剔除其中含有明显错误数据的样本（θ-h 数据对明显为异常值），得到筛选后的样本共计408 个，其中包含饱和水力传导度Ks数据的样本共247 个。各质地条件下的土壤样本数量如表1 所示。

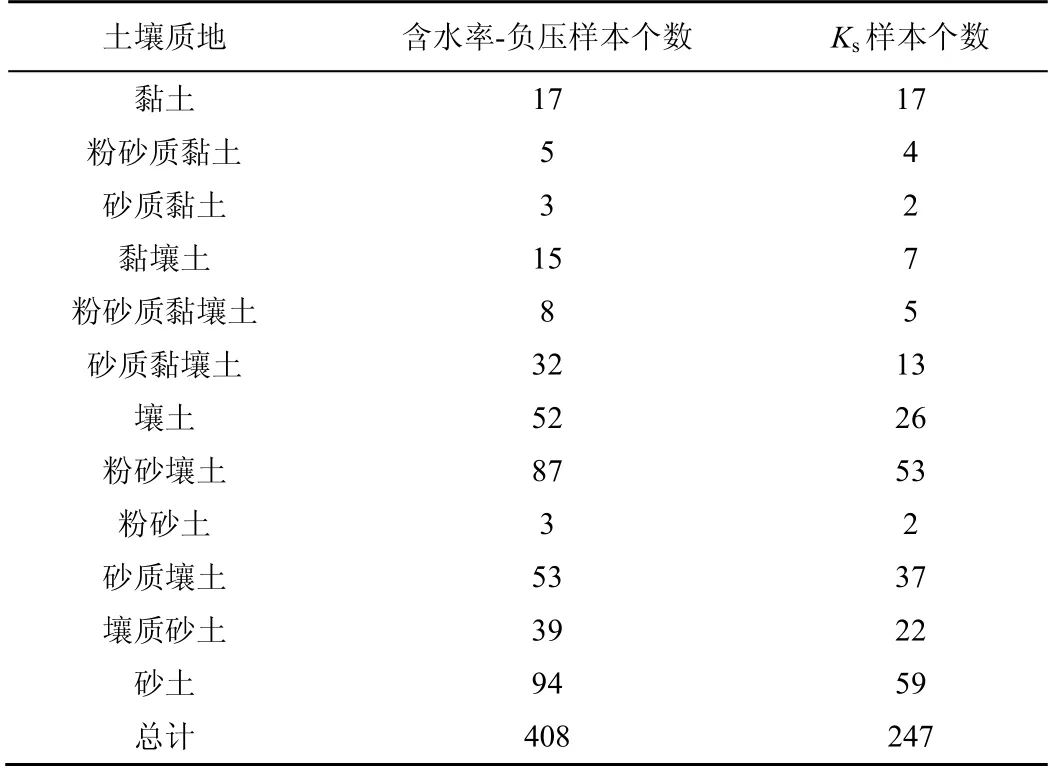
表1 各质地条件下的土壤样本数量Table 1 Number of soil samples for each texture

1.2 数据处理方法

土壤水分特征曲线模型有较多种，其中VG 模型由于其形式简单，适用性好，是当前应用范围最广的土壤水分特征曲线模型。其形式如式（1）所示。

式中：θ 和h 为含水率和负压；θr、θs、α、n 分别为待拟合的土壤水力参数，即本研究所述VG 参数。

对VG 参数进行拟合的方法有很多，本研究拟采用遗传算法与非线性最小二乘法相结合的方法。遗传算法具有一定的随机性，且若终止条件设置不合理，会使得优化结果虽然可以接近全局最优位置，但不一定恰好达到拟合的适应度函数最小的最优解。而非线性最小二乘法可以很好地解决这个问题。本研究使用遗传算法优化的结果作为非线性最小二乘法的初始参数。遗传算法与非线性最小二乘法相结合的优化方式使得拟合结果可以达到全局最优，同时避免了非线性最小二乘法初始参数设置不合理导致的算法不收敛的问题。

在此基础上，利用UNSODA 数据库中的土壤砂粒、粉粒、黏粒百分比、土壤体积质量等基本物理指标为模型的输入，以VG 参数和Ks为模型的输出，建立机器学习模型。对于拟合得到的VG 参数，由于α、n、Ks的绝对值跨越多个数量级，为了获得可靠的预测结果，首先对这3 个参数进行对数化处理。由图1 可以看出，处理后的数据更集中，其中α、Ks更接近于正态分布。此外，在建立机器学习模型之前还需要将数据（包括输入和输出）进行标准归一化处理。处理后的数据被划分为了训练集和验证集。本研究通过交叉验证，测试了训练集和验证集数据的统计分布规律，结果显示其统计量均在正常范围，说明数据集的划分方法具有可靠性。

1.3 土壤转换函数模型方法

本研究拟采用多隐含层神经网络（Artificial Neural Network, ANN）作为待评价的一种机器学习方法。对于预测VG 参数的神经网络模型，通过超参数搜索，平衡模型复杂度与模型过度拟合的程度。本研究拟采用包含4 层隐含层的神经网络，各层神经元数目分别为10、12、5、13。对于预测Ks的神经网络模型，由于建模所用的数据量较少，因而拟采用3 个隐藏层的神经网络结构，各层神经元数目分别为10、5、5。

支持向量机（Support Vector Machine, SVM）最初是用于分类的一种机器学习方法，其原理是通过构造适当的核函数，将数据点投影到高维空间，然后在数据点之间寻找最大边缘超平面作为决策边界，由于该决策边界取决于离决策边界最近的若干数据点，即支持向量，故该方法被称为支持向量机。在回归问题中，超平面即为所建立的回归模型。支持向量机有坚实的理论基础，适用于小样本数据量的运算，故本研究选取支持向量机作为一种待评价的机器学习方法。本研究的支持向量机模型采用高斯径向基核函数，并通过参数搜索选取了合适的建模参数。

最近邻居法（K-Nearest Neighbor，KNN）的思路是将特征空间中离待预测样本最近的K 个数据的属性值作为待预测样本的预测值，该方法思路简单直观，预测值取决于周围几个样本点的值，不需要进行模型训练，且在直观上计算结果也较为可靠，因而本研究将该方法作为待评价的一种机器学习方法。本研究中选取的K 值为40。

1.4 评价指标

本研究选取均方根误差（RMSE）和决定系数（R2）作为评价指标。

式中：N 为样本的数据点数量；yi和分别为实际值和预测值；y为数据的均值。

2 结果与分析

2.1 对模型参数的预测效果

各模型在训练集和验证集上预测VG参数的效果如图2 所示。从图2 可以看出，模型预测饱和含水率θs和n 的效果较好，而预测残余含水率θr和lg(α)的效果较差，可能是由于其数值的绝对值较小，接近于0，因而在以决定系数为评价指标时，效果较差。

从训练集和验证集来看，各模型的训练集的预测效果大部分要略好于验证集。值得注意的是，参数lg(n)在验证集上的表现效果要优于训练集，可能的原因是由于数据集样本量较小，使得某些异常值留在了训练集中，造成了训练集的预测效果反而降低。

从所选用的模型来看，在验证集上，ANN 预测的饱和含水率θs和lg(Ks)明显好于SVM 与KNN，且在其他参数上的预测效果也不明显弱于别的模型。而SVM 模型在验证集上对于lg(n)的预测效果较好，且在预测其他参数的时候也仅次于ANN 模型。

2.2 对样本的预测效果

以UNSODA 数据库中编号1351 的土壤样本（该样本被划分在验证集）为例，预测得到的土壤水分特征曲线数据与实测数据点如图3 所示。该样本使用ANN、SVM、KNN 预测参数并得到VG 模型的RMSE分别为0.0118、0.0159、0.0139。

对于整个数据集上样本的表现，如表2 所示。从总体上，SVM 在训练集和验证集上均有较好的表现，ANN模型次之，KNN模型的表现稍逊于其他2个模型。

为了直观显示各机器学习模型对不同土壤质地样本的预测精度，本研究将各模型的预测效果在土壤质地三角形中进行了展示（图4）。由图4 可知，SVM 模型对各土壤质地在训练集和验证集上都有较为均衡的表现，ANN 模型的预测效果次之，但对于黏性土的预测效果逊于SVM 模型。对于KNN 模型，无论在验证集还是训练集上，对于处于土壤质地三角形边缘的样本的预测效果欠佳，尤其是在样本稀疏的区域。这可能是由于KNN 模型在进行预测时只与最临近的若干点有关，而对于土壤质地三角形边缘的数据点，由于边缘数据点较少，预测效果较差。

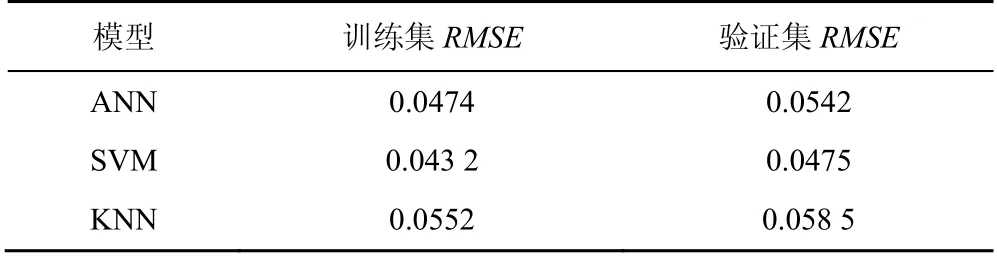
表2 各机器学习模型的效果Table 2 The performance of each machine learning model

2.3 各模型运行效率比较

模型运行效率如图5 所示。对训练数据，ANN建立模型所需要的时长最长，而SVM 模型次之，KNN模型所需时间最短。而对验证数据来说，ANN 模型预测用时明显低于其他2 个模型。

从原理上来看，ANN 模型在训练时，需要进行迭代运算，使得计算成本加大。然而，对于训练好的模型，计算时只需将待预测的数据输入模型，无须进行迭代运算即可获得所需的参数，因此，模型在训练与预测上的用时可能会相差若干个数量级。KNN 模型并不需要训练，而只需要数据读入电脑内存，KNN模型的训练用时即为数据传输的用时。在模型预测时，KNN 模型需要将待预测数据距离每个训练集中数据的欧氏距离计算出来，并进行排序比较，故模型预测用时会远大于训练用时。

需要指出的是，虽然ANN 模型训练耗时较长，但对于大型数据集，可以采取mini-batch 等方法在基本不增加或少量增加计算成本的同时处理更大量的数据。ANN 模型在验证或预测时，训练模型常常已完成，无须考虑ANN 模型训练耗时较长的问题。因而，在大型的数据集上要综合考虑计算成本、预测精度等方面，ANN 模型在大数据集上构建土壤转换函数模型具有较大的优势。

3 讨论

将所建立的ANN，SVM，KNN 模型与广泛使用的Rosetta 模型[19]进行对比。Rosetta 模型是2001 年提出的，并耦合于RETC、Hydrus 等土壤常用软件中。其中，该模型根据输入数据信息量的多少，分为5 个子模型，H1 模型只输入样品的土壤质地分类；H2 模型输入样品的砂粒、粉粒、黏粒百分比（SSC）；H3模型增加了土壤体积质量（BD）；H4 模型增加了在330cm 负压下的含水率（θ33），通常认为该含水率可以代表田间持水率；H5 模型增加了在15000cm 负压下的含水率（θ1500），通常认为该含水率可以代表植物萎凋点。Zhang 等[11]根据样本拟合效果进行加权，对Rosetta 模型进行了改进，在各模型后加字母“w”表示（如H1w 等）。各模型对样本含水率的预测效果（RMSEw）如表3 所示。

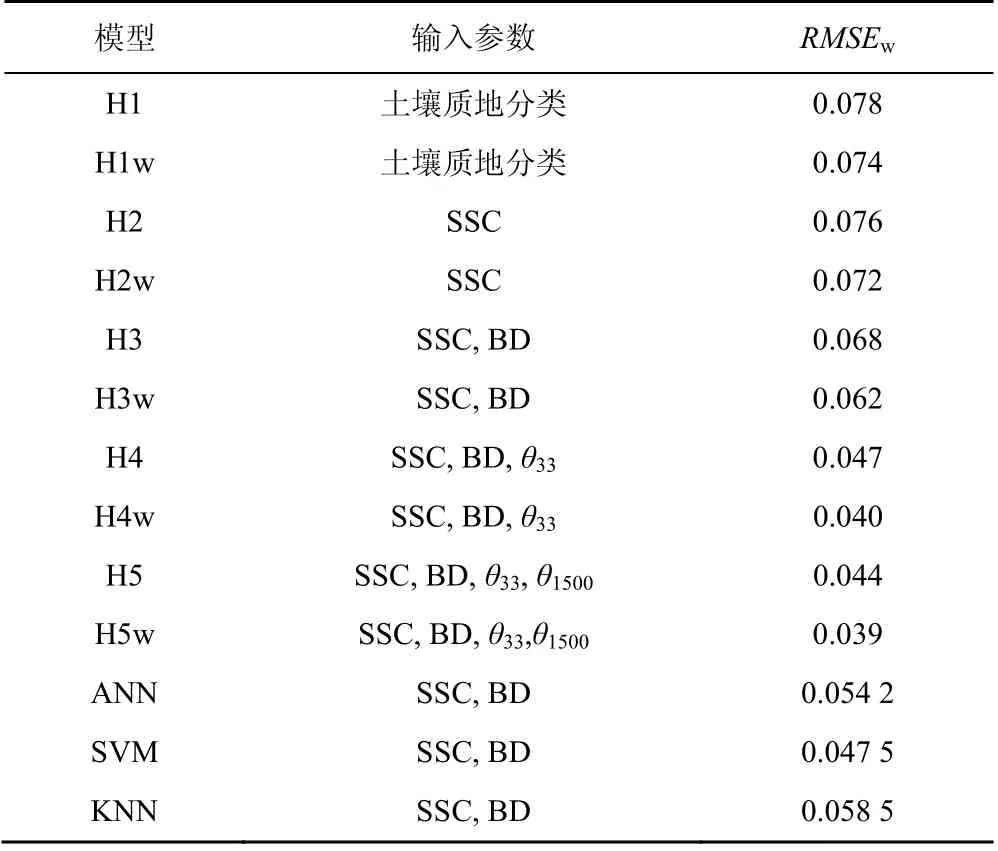
表3 本研究建立的模型与Rosetta 模型的比较Table 3 Comparison between the model established in this study and the Rosetta model

由表3 可知，随着输入数据信息量的增加，Rosetta 模型的各个子模型的预测精度均有所增加（从H1 到H5，或从H1w 到H5w）。而在同一层级，对样本进行加权改进后的模型（H1w 到H5w）较原模型（对应的H1 到H5 模型）均有所提高。本研究建立的ANN，SVM，KNN 模型与Rosetta 模型的H3 或H3w 子模型所使用的输入数据信息量相同。然而，Rosetta 模型由于采用单隐含层神经网络，模型结构简单，其预测精度仍低于本研究使用的ANN 模型，说明增加模型的复杂度对于提高预测精度有积极意义。而本研究建立的KNN 模型和SVM 模型同样优于H3 模型或H3w 模型，说明改进建模方法同样有利于提高预测精度。

值得注意的是，建立Rosetta 所使用的样本容量更大，而本研究所采用的UNSODA 数据库只是建立Rosetta 所使用的样本的一部分。因而，在对比模型效果的时候，还应该仔细考虑样本量及数据质量对标定模型的影响。

4 结论与展望

4.1 结论

1）从VG 模型的参数预测来看，ANN 模型和SVM 模型均优于KNN 模型，且二者对于不同的参数预测效果各有优劣。从样本的预测效果来看，SVM模型在训练集和验证集上的预测精度要优于另外2个模型，ANN 次之，KNN 逊于SVM 与ANN。

2）从模型运行效率来看，在训练集上，ANN 建立模型所需要的时长最长，而SVM 次之，KNN 所需时间最短。而从预测用时来看，ANN 模型预测用时明显低于SVM 和KNN 模型。

3）SVM 模型的样本预测精度最优，然而，SVM模型的计算复杂度会随着数据量的增加而呈二次方增加；相对而言，ANN 算法在大数据量的时候可以选取mini-batch 等方法在基本不增加或少量增加计算成本的同时处理更大量的数据。因而，本研究推荐在小数据集上使用SVM，而在更大型的数据集上要综合考虑计算成本、预测精度等方面合理选取土壤转换函数模型。

4.2 展望

由于土壤取样和土壤水分特征曲线测试成本很高，本研究使用的UNSODA 数据库样本相对稀疏，导致其代表性并非特别好。随着全球土壤物理数据库的发展，数据量的增加、土壤水力特性的影响因素信息的进一步完善性，数据库的代表性会进一步增强，届时可以建立适用性更佳的土壤转换函数模型。

限于研究者的水平和本文的篇幅，关于土壤转换函数，仍可以进行相关的探索，如在大型数据集上按照区域或土壤类型分组对土壤转换函数的精度是否有提高效果；土壤转换函数的不确定性来源以及可靠性如何量化；更合适的、可解释性更好的土壤转换函数建模技术；增加哪些土壤信息输入最有利于提高土壤转换函数的预测精度等。

致谢：感谢天津大学地球系统科学学院张永根副教授在数据库选取和土壤转换函数理论方面的指导和帮助。