实验为主、信息化为辅的立体几何教学探索
——以“平面与平面所成的角”为例
宁波经贸学校 孟晓安
虽然中职学生的数学基础薄弱,对待数学兴趣淡薄,在立体几何上更是“老大难”,但他们动手能力强,喜欢在实践中学习,喜欢上台展示自我,喜欢口头表达多过书面表达。
课堂活动的开展往往基于学情,秉承这一种理念,笔者采用“以实验为主,信息化为辅”的方式开展“平面与平面所成的角”的教学。
一、动手实验,猜想概念
建构主义学习理论认为:学习是引导学生从原有的经验出发,进而生长或建构起全新的经验。而对于立体几何教学体系的建构,需遵循“直观感知—操作确认—推理论证—度量计算”这四个认知过程。
基于以上,笔者采用实验为主、信息化为辅的混合式教学方式,帮助学生突破“二面角及其平面角”的概念这一教学重点,化解“二面角及其平面角”的确定这一教学难点。
1.实验一:初识二面角大小
任务一:折出二面角。
在 4 张彩色小卡纸上各画出一条线,沿着这条线将卡纸对折,然后打开进行观察。
任务二:给二面角排排队。
请按你的理解给这些二面角模型排排队,并说出这样排的理由。
提问:这个大小你是怎么看出来的?此时眼睛的视线和二面角的棱呈现什么位置关系?
设计意图:通过实验一的两个任务,让学生在潜意识中感受二面角的平面角及其大小,并通过及时提问,帮助学生初步了解二面角的平面角的概念,为下一环节做了铺垫。
2.实验二:呈现二面角大小
任务三:二面角的投射。
用手电筒模拟眼睛视线,按你们排列的顺序对模型进行一一投影,使得屏幕上出现的图像是一个平面角,并将这个平面角用笔描在屏幕(或A4纸)上。
提问:(1)对比描出的角与观察到的角的排列顺序是否一致? (2)平面角的两边和顶点分别由二面角的哪部分投影而来?

设计意图:通过投射活动,将二面角的平面角直观呈现在白纸上,体会降维的思维方式。
3.实验三:刻画二面角大小
下面这些模型,能否通过手电筒投影的方式找到它的平面角?


4.任务四:摆角和比角
请同学用算术棒在你们的模型上摆出它的平面角,并将摆出的角与其投影在屏幕(或A4纸)上的角(投影时用笔描在屏幕上了)比较。
提问:哪些作品摆放正确?观察正确的作品,角的顶点落在哪里?两条射线落在哪里?与棱呈现什么位置关系?

5.任务五:猜想概念
二面角的平面角的概念:过( )上的一点,分别在二面角的两个( )内作与棱( )的射线,以这两条射线为边的( )。
设计意图:通过手电筒投射去找二面角的平面角的方法是具有局限性的,因此,通过摆角和比角实验,帮助学生猜想出二面角的平面角的概念。
二、论证、完善概念
实验往往存在误差,此时借助信息化手段可以弥补实验带来的误差。
验证猜想:请看小视频,看看你们的猜想是否正确。
展示如下动画:
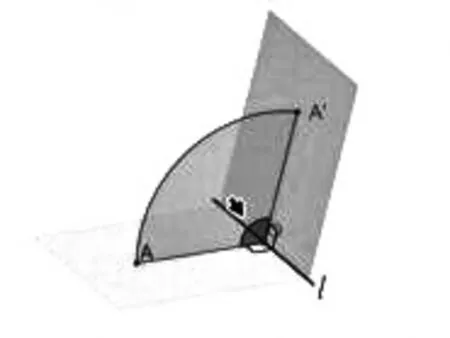

提问:这个二面角的平面角的范围是什么?
展示如下动画:
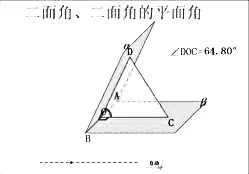
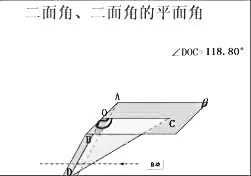
设计意图:通过观看小视频,论证并完善定义,同时得到二面角的平面角的范围。
纯信息化的立体几何教学,虽然能让学生享受视觉上的“精彩”,但往往会出现“过目即忘”的现象。传统的立体几何教学,一般借助图形直观来研究空间图形位置关系的判定与性质,课堂往往枯燥乏味,慢慢加剧学生的畏难情绪,使得他们普遍感觉“立体几何抽象难懂”。此外,无论是纯信息化或传统的立体几何教学,课堂上的生成往往是教师占据主导地位,学生的主体地位大大削弱,这不利于培养学生的学习主动性和创造性。而采用实验为主、信息化为辅的混合式教学方式后,教师退居幕后,把课堂真正还给学生,实现以生为本。动手实验不仅能让学生延迟数学新知识的遗忘时间,还能弥补薄弱的空间想象能力,提高直观想象、数学抽象的核心素养。
本文止于论证“二面角的平面角”的概念及其确定,此种教学设计是否能够普遍推广,等待更多的教师来交流验证。

