基于机器视觉的人机象棋平面控制系统

朱晨曦，高军伟，房国栋，孔德帅

（青岛大学 自动化学院，青岛 266071）

0 引言

作为娱乐机器人的一个分支，人机象棋正逐渐成为人们研究的热点。早期，人们通过设计和制作电子棋盘传感器的方式定位和识别人机象棋棋子，但制作电子棋盘的过程繁琐；伴随机器视觉的发展，图像处理相关算法被广泛应用，人机象棋在视觉定位和识别方面正深入研究。

象棋定位方面，传统字符[1]的定位方法需要不断调整每个阈值,过程繁琐。文献[2]使用依据圆检测和棋子修正的二次定位方法，存在流程运算时间和个别字符识别准确度的问题；象棋识别方面，关于年轮统计[3]的识别方法虽可避免文字任意性，但特征值与字体有关，王殿君等[4]提出采用BP神经网络对棋子进行识别，但算法过程存在局部极值和拟合现象，收敛速度慢，出现新加样本需对整体重新训练。文献[5]提出的使用文字连通数与孔数的方法，在非理想情况下进行字符识别，受实际光线等因素影响较大。

故针对以上问题，本文以三自由度机械臂为例，以人机象棋平面博弈为任务，通过剪切法和对数极坐标&傅里叶变换的模板匹配法定位与识别棋子，后续调用博弈算法和蚁群算法，结合机械臂运动学的模型分析，给出了人机象棋平面博弈的实现方法。

1 系统总体设计

系统总体设计主要由棋子定位和识别、走法产生、路径规划、机械臂控制四部分组成。

1）摄像头捕捉棋盘图像并传进计算机，计算机使用象棋识别算法识别棋盘信息。

2）结合图像识别结果，通过调用博弈算法获得棋局下一步走法。

3）将走法赋给蚁群算法规划走法间路径并得出坐标信息。

4）根据坐标信息，结合运动学逆解，Arduino控制机械臂实现棋子起落及平面移动，完成人机对弈，系统框图如图1所示。

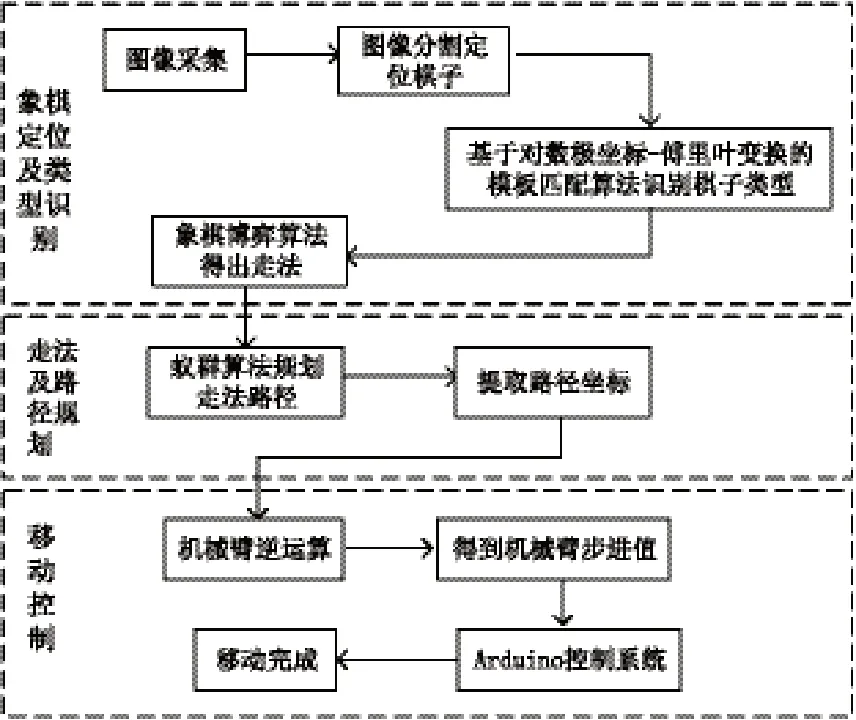
图1 人机博弈系统框图

2 象棋类型定位和识别

2.1 图像预处理

1）桶形畸变矫正 系统使用分辨率1280×1024的摄像头捕捉图像，因镜头使用凸透镜，故需对图像进行桶形矫正，如图2所示。

图2 桶形畸变矫正

2）图像区域裁剪

对于定位问题，由棋盘本身布局所决定，棋子仅会在90个固定交叉点位置起落，故摄像头固定后，利用image viewer分别测出图片90个交叉点坐标值，再根据坐标值依次将整张图片裁剪成以各个交叉点为中心的90张小区域图片，并对这些裁剪图片进行内容识别即可。

3）象棋有无与颜色判断

已知RGB颜色模型，转换成HSV彩色空间后通过调整其分量阈值[6]，可对交叉点区域内的象棋有无与颜色进行判断。

4）棋子提取及处理

判断90张小区域图片中存在棋子后，通过中值滤波保存边缘信息；通过灰度二值化和hough变换圆检测法提取图片中棋子，通过腐蚀膨胀使棋子平滑，并统一成50×50尺寸。如图3所示。

图3 提取的棋图

2.2 棋子种类识别

面对棋子在移动时存在的旋转变化量问题，本系统使用对数极坐标&傅里叶的模板匹配法[7]识别旋转量棋子。将棋子图像的旋转变化经对数极坐标变换转化为平移变化，再结合Fourier平移变换的模值不变性，实图像的旋转不变性。

2.2.1 对数极坐标变换

在图像处理中，对数极坐标变换是将图像从笛卡尔坐标系（x，y）经极坐标系（ρ，θ）过渡后,转换至对数坐标系（u，v）[8]，转换公式为：

式中，（xc，yc）为坐标变换中心，k1，k2为如需放大图像所引入的细化常量。图4为笛卡尔-对数极坐标对应示意图。

图4 笛卡尔-对数极坐标对应示意图

根据式(1)，当原图像旋转βrad时，有：

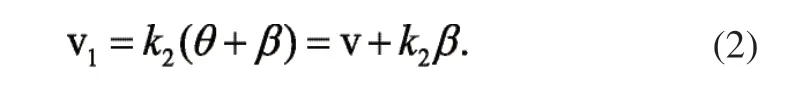
式中，v和v1表示对数极坐标中图像转动前后对应的横坐标。由此可知，笛卡尔坐标系中旋转变化可转化成对数极坐标系中平移变化。图5为棋子“车”在不同旋转角度下的平移变化。

图5 图像旋转及对数极坐标变换

2.2.2 傅立叶变换

在时域空间中，傅里叶变换的模值具有平移不变特性。在图像处理时，图像给出的信号为二维离散型，所以采用二维离散傅里叶变换[9]。则尺寸M×N的图像函数f（x，y）对应二维离散傅里叶变换f（u，v）为：

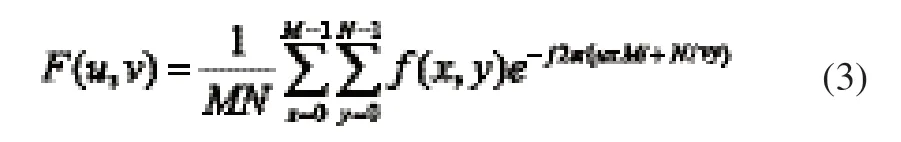
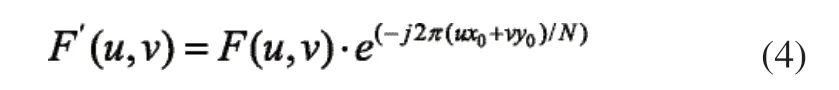
得到平移前后的模值为：

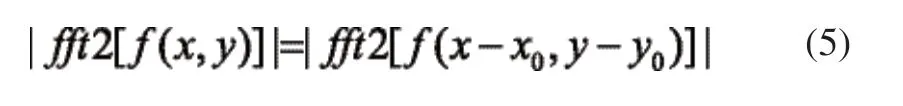
由此模值知，其时域平移不变的特性，故图像通过式(1)～式(5)实现自身旋转不变性。

2.3 算法检验与结果

为检验算法效果，本文利用11张各类型的棋子图片进行测试，分别对这些图片做出一定的角度转动，并计算转动前后两张图像间相关系数。计算如表1所示。

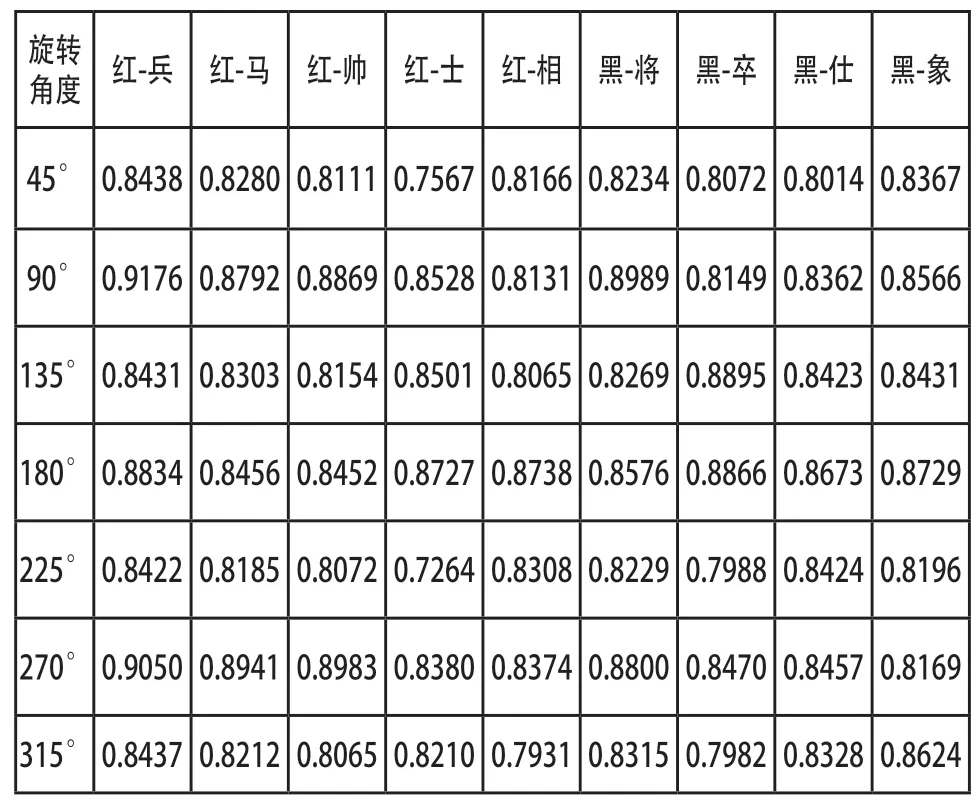
表1 棋子转动前后两图像间相关系数

表中数据知，部分角度如90°270°时相关系数良好，部分角度如45°、135°时相关系数稍低点，其主要是受亮度、位置等实际因素的影响。

为建立模板库，对11种棋子类型的每种图片（对于颜色不同但变换相同的棋子，黑車和红車，黑炮和红炮，黑馬和红馬则归为一类），每张依次选择0°、10°、20°、30°、40°、50°、60°、70°、80°各9个不同旋转状态的图片，共 99张图片作为模板储存和调用。

综上过程，本系统棋子识别流程为：

1）建立模板库。

2）判断裁剪的90张小图片中有无棋子及颜色，再经灰度、二值化等步骤提取棋子。

3）将待识棋子图像和模板库里的图像作对算法变换并得到相关系数，最后将其匹配至模板库中相关系数最大的一类。匹配结果如空白、黑将、黑车等分别用0、1、2等数字表示。

4）以10×9的矩阵形式呈现出所识别的90张小图片数字结果，以利于后续博弈及蚁群算法对识别结果的调用。

5）下次识别重复步骤2）～4）。

为测试识别方法的有效性，本文选取100张棋子位置、旋转方向皆不同的棋盘图像在MATLAB环境下运用，经检测，识别后正确率约为98%。

每当棋子完成移动，棋盘出现变化的位置，有且仅有两处，所以不需对全部90张区域小图片进行重复识别，只需对位置发生变化的小图片进行识别。故系统选用差分法[10]对每张小图片信息是否发生变化进行判断，之后对信息变化的小

图片按序识别其内容，并以新的10×9数字矩阵显示结果，可有效提高系统识别速度与可靠性，图6为棋子识别结果。

图6 棋子识别结果

3 中国象棋人机博弈算法

博弈算法的作用是列出棋局当前所有可能走法，并在可能走法中搜索得出最优走法，最后用四个数字，如1234的形式（1行2列移至3行4列）将走法表示出来，其共有四个核心部分。

棋盘表示部分，通过使用[10]×[9]的二维数组方式来存取棋盘信息，在棋盘上每一个交点[11]都对应数组中一个字节，所呈现的数值则代表在此交点有无棋子或种类。

走法部分列出棋局当前所有可能走法，由估值部分对局面当前情况进行优劣评估，后经搜索部分搜索出最佳走法。搜索部分选用Alpha_Bate剪枝搜索算法，具有减少不必要节点搜索的优势。

c++为人机博弈算法编程语言，Visual Studio 2017为其开发平台，先在开发平台中调试好该博弈算法，然后再通过MATLAB软件的mex功能使MATLAB能对其进行读取。将视觉识别所得的数字矩阵传入象棋人机博弈算法，通过节点搜索，择优得到棋局下一步走法，之后调用蚁群算法，对棋子走法间平面移动路径进行规划。

4 路径规划

棋子存在两种移动，一种按走法移动，另一种被吃掉后放在指定位置的移动。蚁群算法的作用是对棋子平面移动路径进行避障规划，避免棋子在平面移动中受其他棋子的阻碍。

4.1 路径产生

系统对博弈算法当前调用的10×9棋盘数字矩阵进行实时扩充并栅格化，有棋子位置置1，其余位置置0，最终得到一个20×20的01矩阵。

在棋盘栅格中，粒子和障碍物面积应都按照象棋半径大小膨化，即将粒子视为一个质点时，粒子只能沿栅格水平或竖直方向移动，即满足：

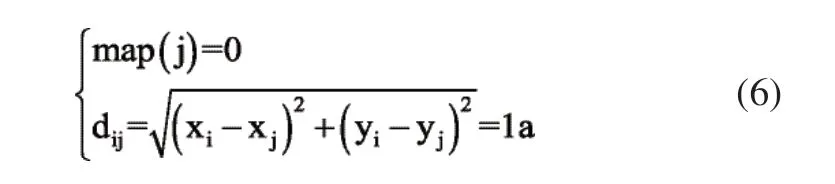
式中，i为质点当前栅格，j为质点下一栅格，a为栅格边长，map（j）为非障碍栅格，dij为栅格i和j间距离。

棋局栅格化后，经蚁群算法得出的转移概率为相邻栅格中心节点间的选择概率[12]，在t时刻，蚂蚁k从xi转移至xj的概率公式如下：

式中，α为信息素浓度相对重要程度，τij（t）为信息素浓度，β为启发性因子相对重要程度ηij（t）为实际距离倒数。图7为棋子被吃掉后从当前位置移至棋局外指定位置的路径仿真图。

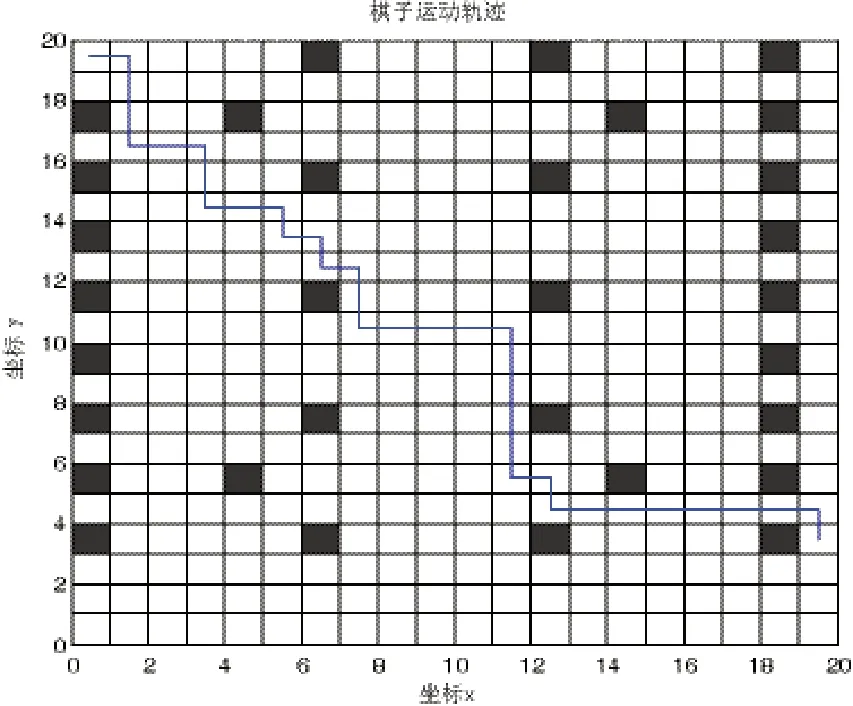
图7 路径图

将博弈算法所得走法起止点换算成栅格号，赋给蚁群算法后得到一条由起止栅格编号及无障碍栅格编号结合的路径，可用一维数组表示，并保存在文本中，以备坐标转换。

4.2 坐标定位及转换

栅格坐标系中坐标，并不能直接作为机械臂起落棋子的定位坐标，须将其从栅格坐标系{B}转换到机械臂基底坐标系{A}下表示。

如图8所示，{B}为栅格坐标系，{A}为基坐标系。xB、yB表示棋子在栅格坐标系OB下的位置，xA、yA表示棋子在基坐标系OA下的位置。

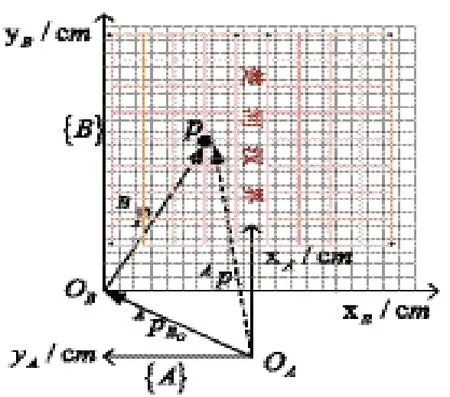
图8 坐标系

棋子位置及移动路径皆对应一个小栅格编号，每个小栅格号都可换算成直角坐标下小栅格中心位置[13]，换算公式如下：

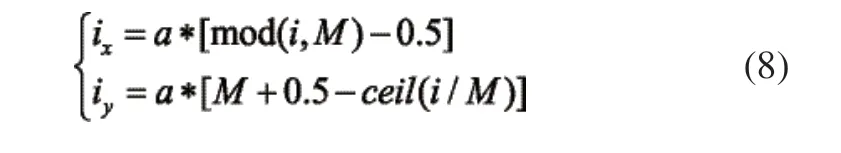
式中，a为小栅格边长，i为栅格编号，为每行栅格个数，mod()为取余，ceil()为正方向舍入，（ix，iy）为栅格中心直角坐标。

根据式(8)可得到棋子在栅格坐标系中位置，但要作为机械臂末端最终用来抓取的定位坐标，还需要将其转换至基坐标系{A}下表示。对本系统三自由度机械臂而言，末端执行器只需要描述其位置，通过式(9)进行旋转变换和平移变换二者的相加，可得点p相对于基坐标{A}的最终定位坐标Ap。

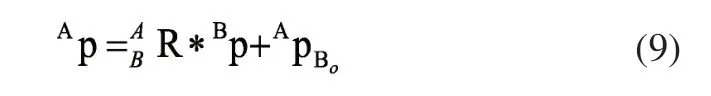
将蚁群算法得到的路径栅格号代入式(8)、式(9)可得棋子在基坐标{A}下的最终定位坐标。将其横纵坐标值分别放入px，py向量中，机械臂在抓取棋子时，需确定棋子在三维空间下的坐标[14]，故令设一组定值向量pz，表示棋子在空间中的高度。

5 机械臂控制

三自由度机械臂结构，如图9所示，腰部作水平方向旋转运动，大臂和小臂作垂直于基座水平旋转平面的俯仰运动。小臂尾部装配一个电磁铁，通过控制其电磁得失来控制对棋子的取置。图10为本系统实物图。

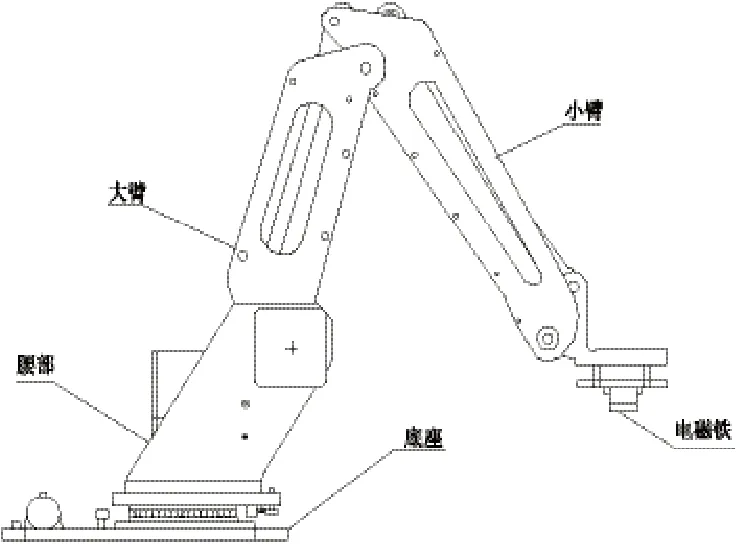
图9 机械臂结构图

图10 系统实物图

要想使机械臂末端准确的运动到棋子上方，需要控制好每个机械臂关节转动的角度。为此，系统需要通过已解算得的定位坐标代入机械臂逆运算，求取每个机械连杆的转动角度。对本系统的机械臂建立如图11所示的连杆坐标系，然后结合表2中连杆参数，通过D-H法[15]建立三轴机械臂运动学模型。

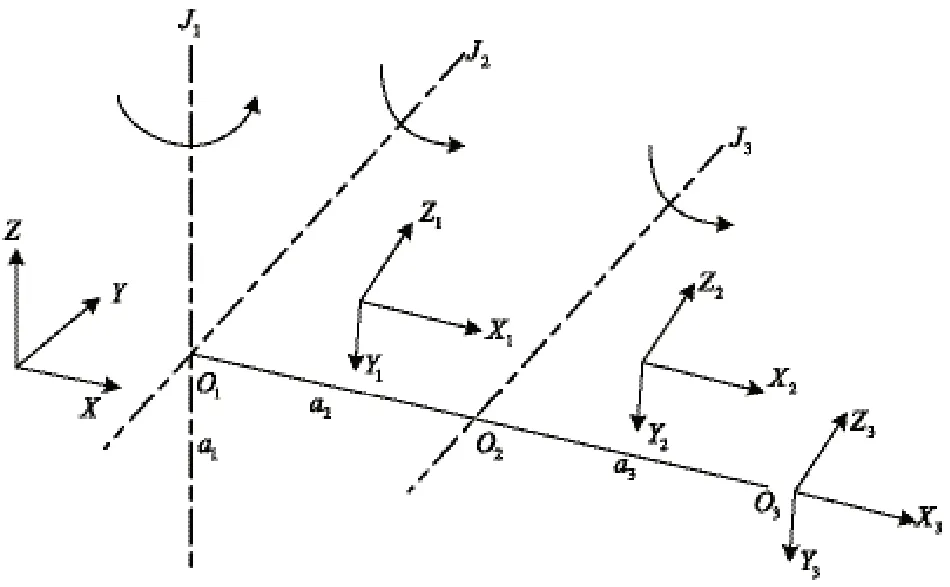
图11 机械臂连杆坐标系

根据表2和式(10)所示的相邻两连杆坐标系间变换法则求取机械臂正解，可到机械臂末端与基坐标系{A}之间的变换矩阵，如式(11)所示。

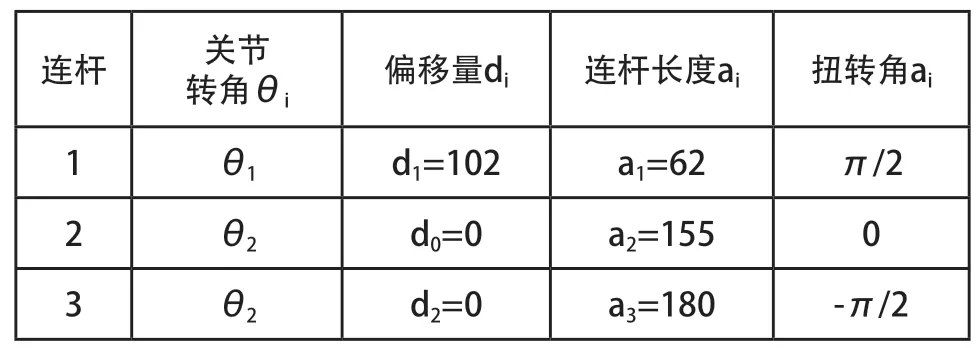
表2 各关节D-H参数表

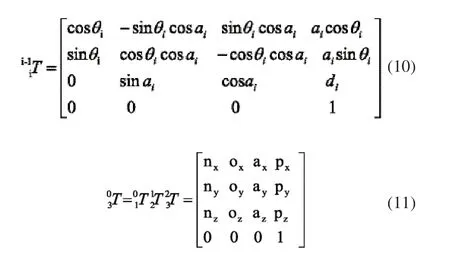
式中，nx、ny、nz，ox、oy、oz，ax、ay、az分别为机械臂末端坐标系x、y、z轴在A坐标系中的方向矢量，px、py、pz表示机械臂末端位置在基坐标系中的坐标。

然后求取机械臂逆解，用未知的连杆逆变换同时左乘式(11)两端，把关节变量分离[16]出来，从而得到即：

令方程两边元素(4)、(5)、(6)分别对应相等得：

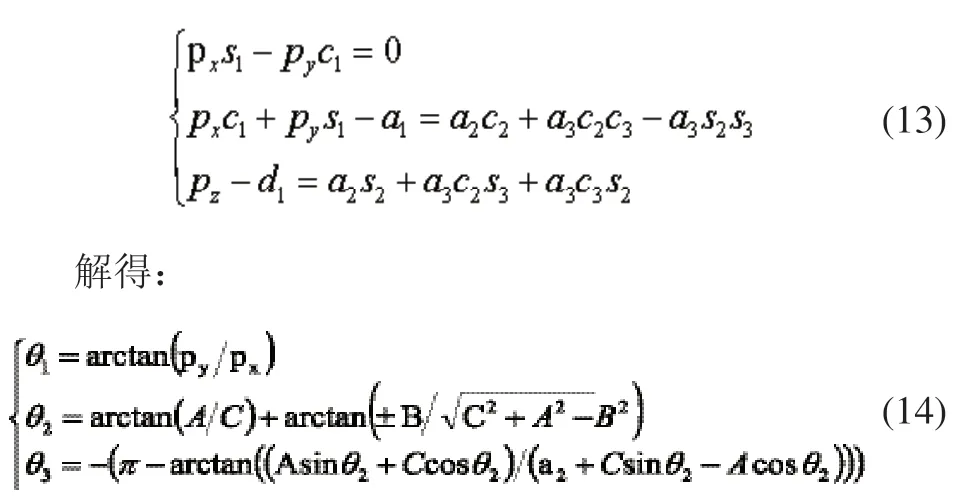
此时，只需要知道机械臂末端即将运行到目标位置的情况[17]，即知道工件的定位坐标px、py、pz，便可得到每个机械连杆的转动角度。

6 系统测试

本系统机械臂核心处理器采用Arduino控制板及Arduino IDE编程环境，机械臂为三自由度机械臂，控制机械臂运动的步进电机通过A4988驱动模块控制，Arduino与A4988之间为脉冲宽度调制。为保证精度选用1/16步进模式，搭配自身10:1减速比，步进电机转动一圈需32000个步进脉冲，即每个脉冲驱动电机转动0.01125°。摄像头捕捉棋盘图像后，经计算机处理得到棋子及路径坐标值，将其代入运动学逆解[14]得出转动角度，根据公式steps=θ/0.01125得到每个机械臂转动步进值，之后将步进值经串口通信发送给下位单片机，下位单片机得到上位机的控制命令后，通过控制每个机械臂的步进电机实现机械臂平面运动。

最后对系统进行整体测试。马的实验测试数据如表3所示，图11为对弈中马的执行过程。

图11 对弈棋子执行过程

表3 实验测试数据

7 结语

本文设计基于机器视觉的人机象棋平面控制系统，棋子正确识别率约为98%，得出棋子当前走法并规划走法间路径后，对棋子和路径所在坐标的定位误差约3.5mm，方向误差小于3°。系统各模块联机后进行人机博弈，各模块间稳定配合，能对棋盘上棋子在平面移动中实现良好的人机对弈，提高了棋子识别率，减小机械臂作业空间，基本达到其设计要求。