基于振动信号分析的滚动轴承寿命预测方法研究

谈智玲，陈才明，徐胜朝，吴志宏，宋寅，王朋飞

（1.湖北华电襄阳发电有限公司，湖北襄阳441000；2.襄阳五二五泵业有限公司，湖北襄阳441004；3.武汉理工大学机电工程学院，武汉430070）

0 引言

电力企业浆液循环泵、氧化风机、球磨机等环保关键机泵可能发生的故障种类、征兆、机理各不相同，很难直接根据征兆对关键机泵设备进行寿命预测。但可针对关键机泵故障多发部件进行预测分析［1］。电动机作为环保关键机泵的核心动力设备与易失效部件，如若发生故障，将会影响工厂其他生产设备的正常运转，甚至会导致整个生产系统瘫痪，给企业带来严重的经济损失。

滚动轴承寿命预测作为电机滚动轴承寿命管理的一个关键步骤，对于电机安全运行尤为重要。通过对电机滚动轴承进行可靠的寿命预测，能够准确掌握电机的运行状况，判断轴承的剩余寿命和故障情况，便于及时制定维修计划。

随着滚动轴承的寿命预测和状态监测理论与技术的不断发展，电机轴承寿命管理系统的预测结果变得更加精准。目前，滚动轴承寿命预测方法主要包括以下3种［2］。

（1）基于力学的滚动轴承寿命预测。该方法主要从滚动轴承的失效和破坏机理的动力学特征来预测滚动轴承的剩余使用寿命。文献［3］对轴承裂纹的扩展速度展开研究。文献［4］对滚动轴承的接触疲劳进行了研究。文献［5］等基于滚动轴承碎裂萌生理论对滚动轴承的寿命进行预测。这些方法普遍存在理论性强，建模困难的问题，在实际工程项目中应用较少。

（2）基于概率统计的滚动轴承寿命预测。该方法是指采用正态分布或威布尔分布模型等，使用大量的轴承试验数据训练模型参数，预测滚动轴承的失效率和可靠性。文献［6］提出了Tallian寿命理论，在L-P模型的基础上优化概率系数。文献［7］根据滚动轴承存在的无限寿命情况和材料的疲劳强度，构建了Y-H模型。文献［8］等提出基于动力学的轴承载荷分布模型。在工程实际应用中，不同轴承的工作状态存在差异，基于部分样本的概率很难满足所有轴承的实际状况，其使用局限性较强。

（3）基于信息技术的滚动轴承寿命预测。包含神经网络、模糊计算、专家系统、进化算法、粗糙集理论等人工智能方法，可以应用于不确定因素较多的电机滚动轴承寿命预测上。文献［9］等采用机器学习——支持向量机方法预测了滚动轴承的剩余寿命。文献［10］等使用神经网络算法预测了滚动轴承的剩余寿命。文献［11］等基于相关系数和反向传播（BP）神经网络算法搭建了滚动轴承的性能退化模型。

剩余寿命预测算法作为滚动轴承寿命管理系统中最为核心的部分，算法的准确性、检测速度和稳定性对滚动轴承寿命管理系统的性能起着关键性作用。针对滚动轴承剩余寿命预测问题具备多类别、多特征的复杂特性，本文通过提取能表征滚动轴承退化状态的特征值作为电机滚动轴承寿命预测的协变量，从而实现对滚动轴承剩余寿命的精准预测。

1 基于小波包样本熵的时频域特征提取

小波包分解理论［12］是由Wickerhauser等在正交小波基的基础上提出的一种新的非线性和非平稳信号的分析方法。小波包分解理论将振动信号的时频平面划分得更加精细，对振动信号高频区域的分解分辨率要大大高于小波变换，能够自适应地选择合适的基函数，与原始振动信号匹配，进一步提高振动信号分解能力。

3层小波包分解示意如图1所示，其中H是低频分量，G是高频分量，S是原始振动信号。

图1 3层小波包分解Fig.1 Three-layer wavelet packagedecomposition

样本熵［13］是表达时间序列的无规律程度和复杂度的定量描述方法。样本熵的值越大，说明滚动轴承振动信号的时间序列越复杂，系统越不稳定；反之表明时间序列自相似度越高，序列取值也更加规则。基于滚动轴承振动信号的特点，样本熵能够很好地对振动信号进行分析。鉴于小波包变换能够很好地分解滚动轴承振动信号，而且样本熵能够描述振动信号的复杂性和不规则性，本文把小波包变换与样本熵组合起来，提出一种基于小波包样本熵的时频域特征提取方法，其流程如图2所示。

图2 滚动轴承时频域特征提取流程Fig.2 Feature extraction in timeand frequency domainsfor a rolling bearing

归一化后的8个频率子带的样本熵在滚动轴承全生命周期中的变化过程如图3所示，其中第1，4，5，6，7，8子带的样本熵，在轴承正常工作时期保持稳定，随着轴承磨损加剧，产生突变并持续呈上升趋势；第2子带的样本熵随采样次数的增加产生的变化比较混乱，相关性很弱；第3子带的样本熵随着轴承的磨损加剧呈下降趋势，有一定相关性。

图3 基于小波包样本熵的振动信号时频域特征集Fig.3 Featureset of vibration signal in timeand frequency domainsbased on wavelet packet sampleentropy

2 基于皮尔逊相关分析的特征选择

通过时域、频域、时频域特征提取获得的振动信号特征参数多达20种，它们与滚动轴承的磨损状态及剩余寿命预测的相关程度各不相同。剔除这些与轴承剩余寿命预测相关性不大的特征参数，能提高寿命预测的精度和准确性。

皮尔逊相关分析法是目前常用的相关性分析法，它能衡量数据之间的关联程度［14］。数据X与数据Y之间的皮尔逊相关系数为

式中：Cov(X，Y)为数据X与Y的协方差；D(X)，D(Y)分别为数据X与Y的方差。

PCC(X，Y)的取值范围为［-1，1］，其绝对值越大，表示数据X与Y的相关性越大；反之则表示数据的相关性越小。滚动轴承的振动信号的特征参数经过归一化处理后，通过皮尔逊相关分析，获得这些特征参数与滚动轴承剩余寿命值的皮尔逊相关系数PCC，从中筛选出PCC较大的特征参数。

图4展示了滚动轴承全生命周期中获取的振动信号的20种时域、频域及时频域特征参数与PCC的绝对值。

通过图4可以直观地发现这些特征参数与滚动轴承剩余寿命值的相关性强弱关系。图中-X，Xrms，C，Kr，CL，CW分别表示时域特征参数中的绝对均值、均方根值、峰值因子、峭度值、裕度因子、偏斜度；fa，fc，msf，vf，Rvf，S分别表示频域特征参数中的平均能量、重心频率、均方根频率、频率方差、频率标准差、信号能量。sk(k=1，2，…，8)表示时频域特征中前8个小波包分解子频带的样本熵。

本文选取PCC的绝对值大于0.8的特征参数作为滚动轴承磨损分析和剩余寿命预测的特征参数集。由图4可以看出，绝对均值，均方根值，平均能量，均方根频率，频率标准差，s1，s6，s7都是与滚动轴承寿命相关性较大的特征参数。

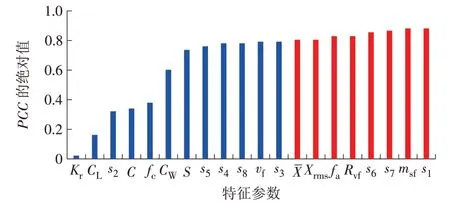
图4 特征参数的皮尔逊相关系数值Fig.4 Pearson correlation coefficientsof characteristic parameters

3 基于改进PSO-GRNN算法的轴承寿命预测模型

3.1 GRNN算法的改进

广义回归神经网络［15］（GRNN）是一种基于径向基神经网络改进的前馈式神经网络。当采集的轴承振动信号样本数据较少时，GRNN有很好的预测效果。

虽然经过皮尔逊相关分析筛选后的特征参数和滚动轴承剩余寿命的相关性都很强，但是在滚动轴承实际工作过程中，转速、动载荷、时域特征、频域特征及时频域特征等相关因素之间存在一定联系，这种联系会导致信息重复，造成GRNN算法的训练速度和预测准确度下降。为了消除这一影响，本文在输入层和模式层之间加入数据处理层，通过主成分分析（PCA）类似的方法对输入层的样本数据进行了压缩处理。以转动速度、工作时间、径向力、特征参数等作为输入的改进后的GRNN 5层网络结构如图5所示。其中，X（x1，x2，x3，x4，…，xk）为神经元输入特征参数，d（d1，d2，…，dp）为数据压缩处理结果，p（p1，p2，p3，p4，…，pm）为神经元的传递函数，s（s1，s2）为模式层输出的神经元求和结果，Y为输出结果。

图5 改进后的GRNN 5层网络结构Fig.5 Improved GRNN with five-layer network structure

假设输入层的观测值是X，函数方程y是输出层的最大概率回归结果，则y的期望为

式中：Y i是第i个样本的输出变量。将f^(X，y)代入式（2），整理后得到GRNN的基本方程为

在改进后的GRNN中，神经元的层数固定为5层且每层神经元的个数可以由输入的样本确定，即可以通过筛选后的特征参数确定。与BP神经网络相比，它不需要设置神经元的层数及激励函数，只需要设置平滑因子，减少了寻优的参数数量。寻找最优的平滑因子σ是影响轴承寿命预测模型好坏的关键因素，本文采用粒子群优化（PSO）算法来寻找最优的平滑因子。

3.2 PSO算法

PSO算法［16］是一种群体智能优化算法，该算法中赋予所有粒子记忆性，在粒子移动的过程中，通过与其他粒子共享信息以获得最优解。PSO算法流程如图6所示。在这个过程中，粒子的初始化及适应度函数的选择尤为重要。

（1）粒子群的初始参数设置：需要初始化粒子群中粒子的位置和速度并设置粒子群的种群大小n、最大迭代次数m、学习因子c1和c2等。本文选取的粒子种群大小n=30，最大迭代次数m=1 000，学习因子c1=c2=2，粒子群搜索范围为(0.01，2.00)，惯性因子采用线性递减的权值策略为其赋值。

（2）粒子群的适应度函数：适应度函数用均方根误差RMSE表示，即滚动轴承寿命预测模型的输出值与期望值之间的标准差，其表达式为

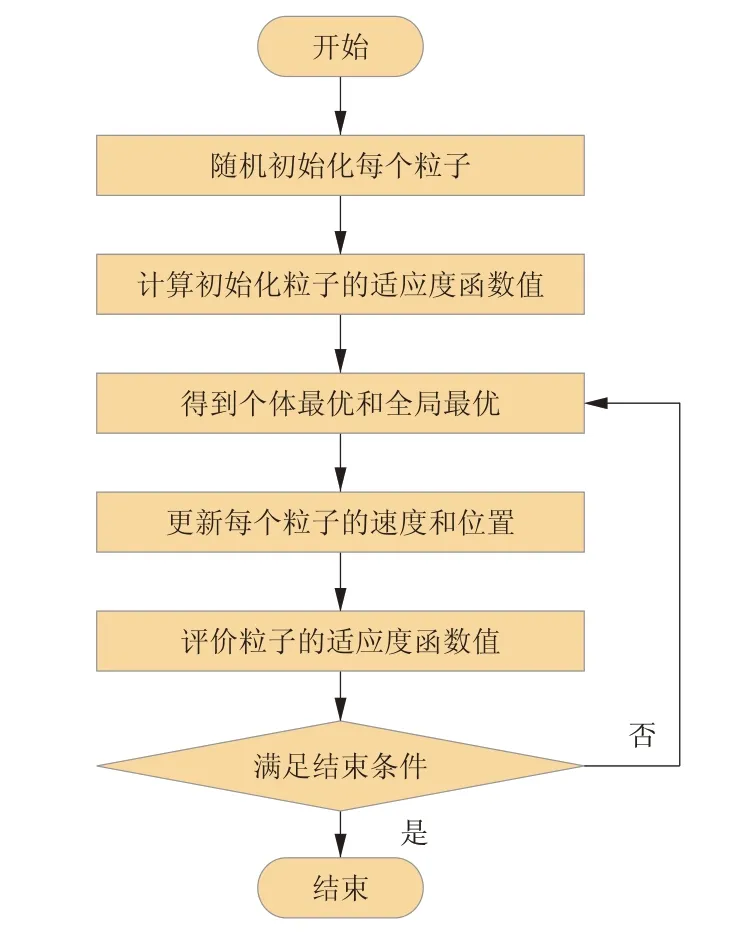
图6 PSO算法流程Fig.6 PSO algorithm flow

式中：Ti和T'i分别表示第i个样本的输出值与期望值。

PSO寻优的过程即寻找RMSE最小值的过程。某次优化过程中均方根误差RMSE随平滑因子在(0.01，2.00)取值的变化过程如图7所示，最后得到平滑因子为0.62时，均方根误差RMSE最小，即其为输出的最优的平滑因子。

图7 RMSE随平滑因子的变化曲线Fig.7 Curveof RMSE varied with thesmoothnessfactor

3.3 滚动轴承剩余寿命预测模型

本文建立的滚动轴承剩余寿命预测模型架构如图8所示。具体步骤如下。

第1步：滚动轴承振动信号采集，对获取的振动信号进行预处理，主要包括去空值和剔除错点。

第2步：对预处理后的振动信号进行特征提取，本文采用小波包样本熵特征提取方法，将小波包分解后的8个子频带的样本熵作为时频域特征参数。

图8 滚动轴承剩余寿命预测模型架构Fig.8 Framework of residual lifeprediction model for antifriction bearing

第3步：通过皮尔逊相关分析法，筛选出与滚动轴承剩余寿命相关性较强的特征参数，能显著提高滚动轴承寿命预测的准确性。

第4步：利用PSO算法求出最优的平滑因子，建立优化后的GRNN模型，再将筛选后的特征参数、转速、径向力等作为学习样本，输入模型中进行训练，建立基于改进PSO-GRNN的轴承寿命预测模型。

第5步：将第1步获取的实时振动数据，通过信号预处理和特征处理后输入到优化后的GRNN模型中得到滚动轴承的预测剩余寿命。

4 滚动轴承寿命预测结果分析

本文选择滚动轴承的转动速度、工作时间、径向力、特征参数等作为学习样本的输入，借助Matlab分析工具对BP神经网络模型和PSO-GRNN模型进行训练，分别得到基于BP神经网络和PSO-GRNN模型的滚动轴承寿命预测模型。在获取滚动轴承振动信号测试样本数据时，选取LDK UER204滚动轴承作为试验对象，水平和垂直方向的加速度传感器固定在轴承外圈上，从而采集轴承振动信息。试验装置如图9所示。

图9 轴承振动信号采集试验装置Fig.9 Bearing vibration signal acquisition and test device

为避免试验出现单一性结果，通过试验装置中的液压加载系统与电动机转速控制器搭配不同的转速与载荷，设定了3种工况进行样本参数的提取，见表1。

本文选取了在试验装置稳定运转时，试验轴承在正常状态、外圈故障、保持架断裂和内圈磨损4种典型状态下的各项数据，整理其时域与频域信号波形如图10所示。其中左侧为时域信号波形图，右侧为对应的频域信号波形图。

表1 测试样本参数Tab.1 Parameters of the test sample

经过PSO-GRNN模型训练后，轴承时域和频域的重构信号波形如图11所示，其中左侧为时域信号波形图，右侧为对应的频域信号波形图。

图10 4种状态下轴承的时域和频域信号波形Fig.10 Time and frequency domains signal waveforms of the bearing in four states

为了验证本文基于改进PSO-GRNN模型的效果，在表1所示的3种不同转速和载荷工况下，采集试验用滚动轴承全生命周期的振动信号，依照时间顺序将采集到的振动信号均匀分为多组样本数据。

将上述样本数据分别利用BP神经网络、PSOGRNN模型、改进后的PSO-GRNN模型各自进行运算，得到试验用滚动轴承的预期剩余寿命，与实际使用寿命进行对比，得到3种模型在3种工况下的剩余寿命预测结果，如图12所示。

其中横坐标为试验轴承各工况的采集时间，纵坐标为剩余寿命百分比。

图11 经过PSO-GRNN模型训练后轴承的时域和频域信号波形Fig.11 Signal waveforms of thebearing in timeand frequency domainsafter the training of PSO-GRNN

由图12可知，BP神经网络模型预测值的波动情况最为剧烈，由于BP神经网络容易陷入局部最优，从而使预测结果不准确。

GRNN神经网络在学习速度、分类能力和逼近能力等方面均优于BP神经网络，但仍存在局部预测值波动较大的情况。

改进后的PSO-GRNN模型的剩余寿命预测性能最好，预测值波动最小，且寿命后期的误差很小，这对轴承寿命预测尤为重要，能够给更换零部件提供更准确的参考时间。

为了定量分析剩余寿命预测算法的优劣，以均方根相对误差RMSEf为指标衡量不同预测算法的预测精度，其表达式为

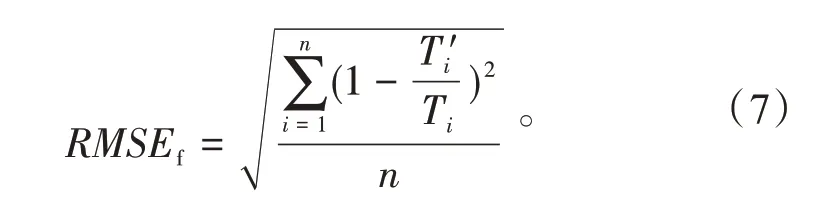
3种模型在3种工况下的滚动轴承预测寿命与实际剩余寿命的均方根相对误差见表2。

由表2可见，改进后的PSO-GRNN模型的均方根相对误差在这3种模型中最小，这也表明了改进后的PSO-GRNN模型的寿命预测值比BP神经网络模型和PSO-GRNN模型更加准确和稳定。

图12 3种模型在3种工况下的剩余寿命预测结果Fig.12 Residual lifepredicted by threemodelsunder three working conditions

表2 不同工况下预测值与实际值的均方根相对误差Tab.2 RMSE between thepredicted and themeasured value with different working conditions %

5 结束语

本文对采集到的滚动轴承振动信号进行时域、频域、基于小波包样本熵的时频域特征参数提取，将提取到的振动信号的高维特征参数通过皮尔逊相关性分析进行筛选，选择出与滚动轴承剩余寿命值相关性较大的特征参数集。将筛选后的特征参数与加工参数作为学习样本，利用基于PSO优化的改进后的GRNN算法构建滚动轴承剩余寿命预测模型并与其他2种方法进行对比，验证了本文提出的滚动轴承寿命预测模型具有更高的准确性及更好的稳定性。