均衡运动旋转振动筛DEM数值模拟

侯勇俊，祝敬涛，李华川，吴先进，蒋锐

（1西南石油大学机电工程学院，四川成都610500；2四川宝石机械专用车有限公司，四川广汉618300；3宝石机械成都装备制造分公司，四川成都610052）

引 言

旋转振动筛广泛应用于采矿、煤炭、石油、化工、电力、食品、环保、医疗等行业对于粉体和胶体的分级[1-5]。单电机旋振筛结构如图1所示，工作时电机带动上下偏心块旋转产生离心惯性力，使与电机固联的筛筒体和筛网（合称为振动体）振动。由于两偏心块产生的离心惯性力的合力不通过振动体质心，上下偏心质量将产生一个激振主矢和一个激振主矩，使振动体随质心作圆运动和绕质心作圆锥摆运动。这种运动使得筛面上的垂直振幅不均匀，存在着颗粒物料向筛面周边扩散较快、物料层较厚、筛分效率较低、颗粒均匀度较差的问题。

图1 单电机旋振筛结构简图Fig.1 Structure diagramof single motor rotary vibrating screen

目前，国内外很多学者[6-11]均采用筛分效率这个指标来评价振动筛在筛分过程中对物料的分离程度，如何提高振动筛的筛分效率一直是国内外学者的研究重点之一。陈亚哲等[12]通过实验比较了不同振动参数对旋振筛筛分效率的影响，并验证了在筛面上作用一均匀纵向超声振动波可以提高旋振筛的筛分效率。杜逸穹[13]通过DEM模拟分析了不同参数对旋振筛筛分效率的影响，并利用BP神经网络得到了一组最佳工艺参数。Alkhaldi等[14]运用离散元方法研究了多层旋转筛在筛分过程中颗粒的透筛、分布及分层情况，比较了不同几何参数和接触参数、连续筛分与批量筛分情况下旋转筛的筛分效率。Lawinska等[15]通过筛网实验，比较了不同工作参数下物料对旋转筛筛孔堵塞的影响。董杏昕等[16]通过改变筛网结构，增大筛网面积，从而提高筛分效率。杨晋[17]设计了一种筛网倾斜式旋振筛，通过反复利用倾斜筛面，提高筛分效率。闫宏伟等[18]分析了不同电动机转速对筛网倾斜式旋振筛物料运动特性的影响，并通过筛分效率实验对仿真结果进行了验证。Sobolev[19]通过实验研究了不同含水量的物料对旋转筛筛分过程的影响。赵平等[20]利用振动电机产生的平旋垂直复合振动设计了一种湿式标准筛旋振筛机，实现了湿式筛分的高效率。谭海军等[21-22]研究了双电机旋振筛的自同步理论，比较了筛面上各点处物料的运动特性。张强等[23]通过现场实验验证了采用多级筛分方式，控制合理的进料速度及将物料进行均匀分散可以提高旋振筛的生产效率。洛传锋等[24]设计了一种圆形转动盘离心式振动筛分机，保证了物料沿筛面分布的均匀性。朱宏政等[25]设计了一种旋转振动筛分机，通过倾斜筛面、多级筛分组、旋转机构和振动机构的共同工作，提高了生产效率与筛分颗粒的均匀度。

国内外学者主要通过调整相关参数及入料方式、增加纵向振动、改变筛网结构、采用多级筛分方式等方法来提高旋振筛的筛分效率，但其基本运动原理均相同。对于不同运动原理的旋振筛，学者们并未从筛分效率的角度进行对比研究。离散单元法（discrete element method，DEM）作为一种计算散体介质系统力学行为的数值算法[26]，在建立参数化颗粒模型及相应接触条件，设置系统特性参数和对几何模型添加动态运动后，即可较为真实地模拟系统颗粒群的流动及颗粒间的碰撞现象，适用于振动筛分过程中对于物料运动特性及筛分效率的研究[27-31]。本文提出了一种均衡运动原理的旋振筛，通过DEM数值模拟，在振幅相似、频率相同的条件下，从筛分效率的角度直观比较了旋振筛在常规运动和均衡运动下的筛面物料运动规律、颗粒粒度分布情况、固相筛分效率及颗粒运动速度，从而来评价哪种运动更利于筛分作业的进行。

1 运动原理及参数计算

1.1 单电机旋振筛

取垂直于筛框体的任一截面，则单电机旋振筛的运动可简化为图2所示。振动体在随质心作圆运动的同时还绕质心作圆锥摆运动，且圆锥摆角位移始终比圆运动位移相位超前1.5π-δ。

图2 单电机旋振筛运动简化图Fig.2 Simplified motion diagramof single motor rotary vibrating screen

振动体在以其静止时质心所在位置为坐标原点的空间固定坐标系下的运动规律可表达如下[32]：

筛面上任一点(x0,y0,z0)的垂直振幅由圆锥摆运动产生，其振幅可表达如下：

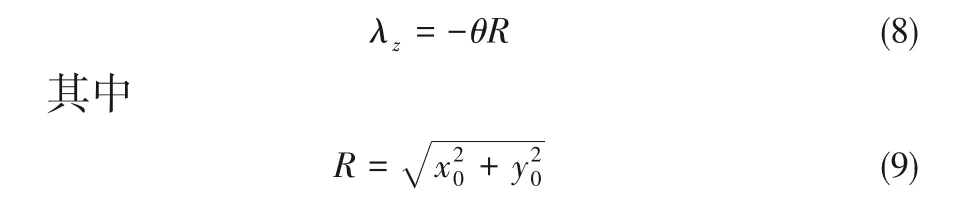
这种运动使得筛面上的垂直振幅不均匀，径向方向上距离筛面中心越远的点，垂直振幅越大。位于同一圆周方向上的点，垂直振幅相同。取筛面直径为600 mm，则整个筛面的平均垂直振幅计算如下：

1.2 均衡运动旋振筛

图3为本文研究的均衡运动旋振筛的一种实现结构。相对于旋振筛质心对称安装的两个激振电机作等速反向旋转，使筛箱实现上下振动。同时，另外一个电机通过皮带驱动偏心转轴发生转动，使筛箱在偏离主轴线一段距离后绕主轴线作周期性的旋转振动。

图3 一种均衡运动旋振筛结构简图Fig.3 Simplified structure diagram of a rotary vibrating screen under balanced motion

筛箱在水平方向上的运动可简化为图4。当系统稳定时，均衡运动可简化为两个自由度的振动，即筛箱绕主轴线方向的往复回转振动和沿主轴线方向的垂直振动。

图4 筛箱水平方向运动简化图Fig.4 Simplified motion diagramof screen box in horizontal direction

振动体在以其静止时质心所在位置为坐标原点的空间固定坐标系下的运动规律可表达如下：

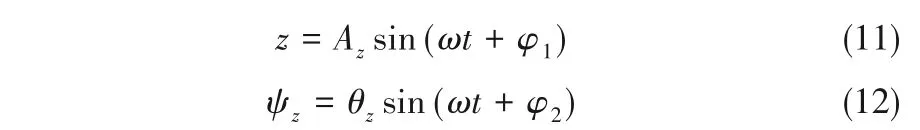
振动体质心运动轨迹满足（水平方向）：

振动体沿主轴线方向作垂直振动和绕主轴线方向作旋转振动，因此筛面上的振幅可分为垂直振幅和水平圆周振幅两部分。其中垂直振幅在整个筛面上都相同，而水平圆周振幅与筛面上点的位置有关。筛面上任一点(x0,y0,z0)的圆周振幅可表达如下：

整个筛面的平均圆周振幅与式(10)计算类似，同理可得整个筛面的平均圆周振幅：

为确保两种运动的能耗相同，即惯性力相等，取平均圆周振幅λˉ=A，垂直振幅Az=λˉz，以保证振幅相似。相位差φ1-φ2=π，以保证旋振方向一致。振动频率23.56 Hz，以保证振动频率相同。

给定单电机旋振筛系统参数如表1所示，其仿真参数通过式(5)～式(7)计算得到，计算结果如表2所示。均衡运动旋振筛仿真参数通过与常规运动旋振筛振幅相似得到，计算结果如表3所示。

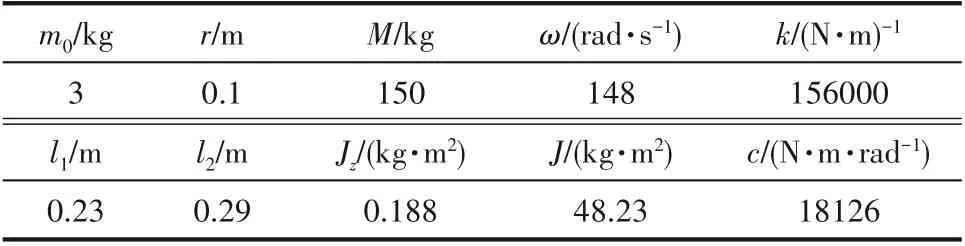
表1 单电机旋振筛系统参数Table 1 System parameters of single motor rotary vibrating screen

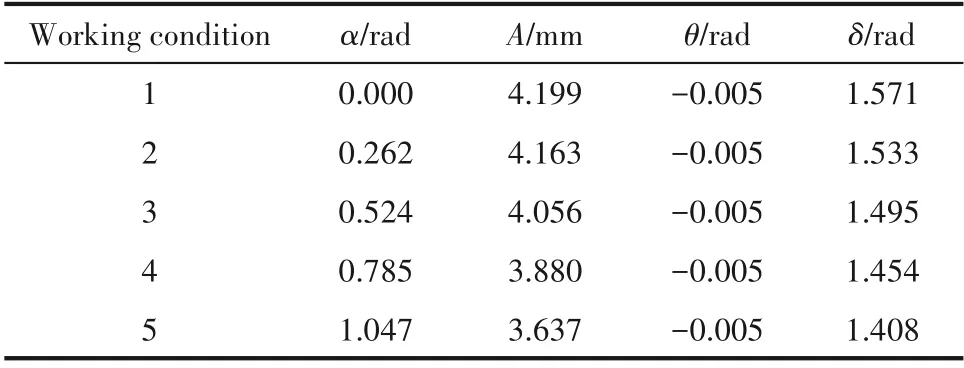
表2 单电机旋振筛仿真参数Table 2 Simulation parameters of single motor rotary vibrating screen

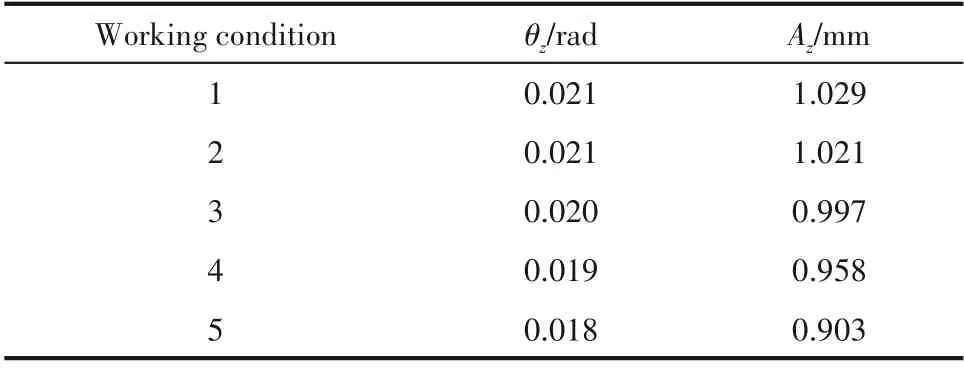
表3 均衡运动旋振筛仿真参数Table 3 Simulation parameters of rotary vibrating screen under balanced motion

2 DEM模拟模型的建立

旋振筛DEM仿真的几何模型如图5所示。其中筛面直径600 mm，筛网厚度10 mm。筛孔为4 mm圆形筛孔，开孔率为34.40%。入料口（颗粒工厂）直径250 mm，位于筛面上方190 mm处。出料管直径100 mm，布置在筛箱圆周方向上。

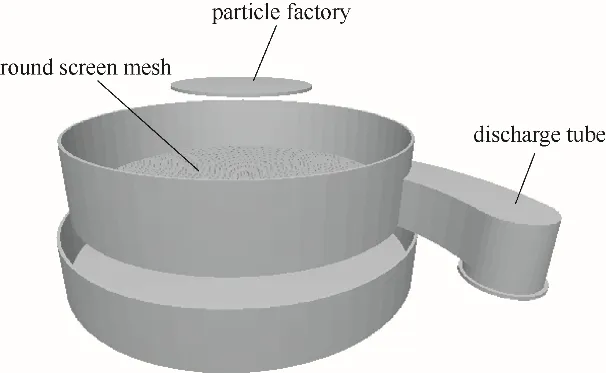
图5 旋振筛DEM仿真的几何模型Fig.5 Geometric model of DEM simulation of rotary vibrating screen

旋振筛主要用于粉体和胶体的分级，且本文主要比较旋振筛在常规运动和均衡运动下的固相筛分效率，暂不考虑颗粒含水量的影响。在其他工作参数相同的情况下，颗粒的形状对筛分结果的影响不大，且球形颗粒能有效提高振动筛DEM的仿真效率[13,33]，故本文将物料单元简化为固相球形颗粒，颗粒接触条件采用Hertz-Mindlin(no slip)模型[34-35]。Rayleigh时间步长取40%，网格总数83200个。入料颗粒由5000个球形颗粒组成，颗粒初速度0.2 m·s-1，进料方式为连续进料，整个仿真时间为5 s。

采用均衡运动工况3工作参数，其他几何参数不变的情况下，改变旋振筛的计算网格数量，使计算网格总数分别达到67680、83200和107800个。三种网格数量下均衡运动旋振筛的固相筛分效率分别为90.73%、90.07%和91.67%，可见，网格数量大于83200时，数值仿真结果变化不大，本文采用83200个网格的仿真结果满足网格无关性。

杜逸穹[13]将实际实验得到的筛分效率与旋振筛DEM仿真得到的筛分效率进行了对比，验证了旋振筛DEM数值模拟的准确性。本文在旋振筛建模及仿真参数设置上虽然与文献[13]有所不同，但针对单电机旋振筛所表现出来的物料运动规律及颗粒速度变化特性是相近的，因此本文旋振筛DEM仿真的模型是有效的。

常规运动旋振筛运动原理如图2所示，在导入EDEM前就应使几何模型先偏离振动体静止时的质心A，同时几何模型应绕振动体运动时的质心偏摆-θ，且圆锥摆初始角位移应比圆运动初始位移相位超前1.5π-δ。将几何模型导入EDEM后，依次按式(1)～式(4)添加动态运动即可（需先添加圆运动，再添加圆锥摆运动，以保证振动体运动时的质心绕静止时的质心作圆运动），振动频率均为23.56 Hz。

均衡运动旋振筛运动原理如图4所示，筛箱除了沿主轴线方向作垂直振动外，还绕主轴线方向作往复回转振动，筛面上任一点的振动表现为垂直振动和水平圆周振动，故在均衡运动旋振筛的DEM仿真过程中不用考虑偏心的影响。将几何模型导入EDEM后，依次按式(11)和式(12)添加动态运动即可，振动频率均为23.56 Hz。

材料特性参数如表4所示，碰撞特性参数如表5所示。入料颗粒粒径分布情况如表6所示。

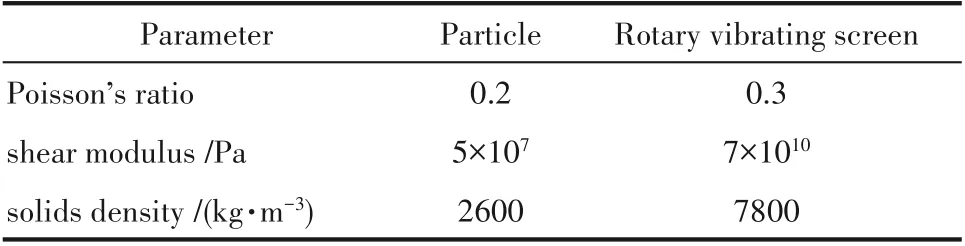
表4 材料特性参数Table 4 Material characteristic parameter

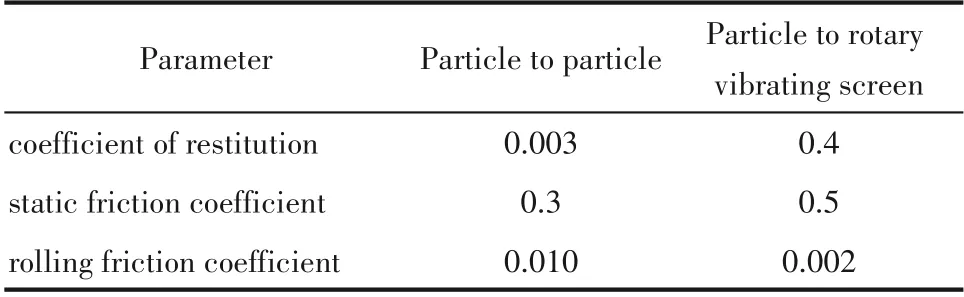
表5 碰撞特性参数Table 5 Collision characteristic parameter

表6 入料颗粒粒径分布情况Table 6 The initial size distribution on particles

3 仿真结果分析

3.1 物料运动规律

旋振筛在常规运动和均衡运动下，筛面上颗粒物料的分布情况分别如图6和图7所示，物料在筛面上的扩散轨迹如图8所示，颗粒迹线的分布情况分别如图9和图10所示。

图6 常规运动筛面上颗粒物料的分布情况（工况5）Fig.6 The distribution of granular materials on the screen surface under normal motion(working condition 5)

均衡运动下，物料在筛面上的扩散轨迹与常规运动（工况2～5）类似，均是从筛面中部以螺旋线轨迹向周边旋转扩散。当物料从进料口落至筛面中部，在圆周切向往复回转力矩和垂直方向激振力的共同作用下，筛面上在除中心外的各点处都在以各自一小段空间螺旋轨迹作高频微幅振动，迫使物料在筛面上作均匀抛掷圆运动。

图7 均衡运动筛面上颗粒物料的分布情况（工况5）Fig.7 The distribution of granular materials on the screen surface under balanced motion(working condition 5)

物料不断地被抛起，因而变得松散和分层。当物料落回到筛面时，小于筛孔尺寸的物料通过筛孔成为筛下物，这部分物料通过旋转扩散从细料出料管排出。筛面上的物料则通过旋转扩散从粗料出料管排出，从而实现物料的分级。

在t=5.00 s，物料基本集中在筛箱周边分布，此时粒群的运动主要表现为颗粒物料绕筛箱周边的旋转输送运动。物料在筛分过程中由筛面中部向周边旋转扩散，两种运动筛分效果的差异已表现得较为明显，暂可不用再增加额外的仿真时间，直至整个筛分过程完成。

图11为两种运动的物料层分布情况。在物料筛分过程中，较大的颗粒会在振动作用下移动到床层上部，而较小的颗粒会移动到床层下部，形成较为明显的分层现象，即巴西果效应[36]。均衡运动下，随着物料在筛面上径向位移的增加，物料层厚度会变得越来越薄，因此就缩短了小粒度颗粒通过大粒度颗粒所组成的物料层而到达筛面的距离和时间，增加了小粒度颗粒与筛面的接触机会，有利于提高颗粒透筛概率。

由于物料向筛面周边旋转扩散，故取同一时刻筛面上一定区域内所有颗粒角速度的平均值作为物料在该区域内的输送速度。物料在整个筛面上的输送速度及在筛面半径0 mm≤R≤100 mm范围内的局部输送速度变化曲线如图12所示。

图9 常规运动颗粒迹线的分布情况（工况5，t=5.00 s）Fig.9 Distribution of particle traces under normal motion(working condition 5,t=5.00 s)

图10 均衡运动颗粒迹线的分布情况（工况5，t=5.00 s）Fig.10 Distribution of particle traces under balanced motion(working condition 5,t=5.00 s)

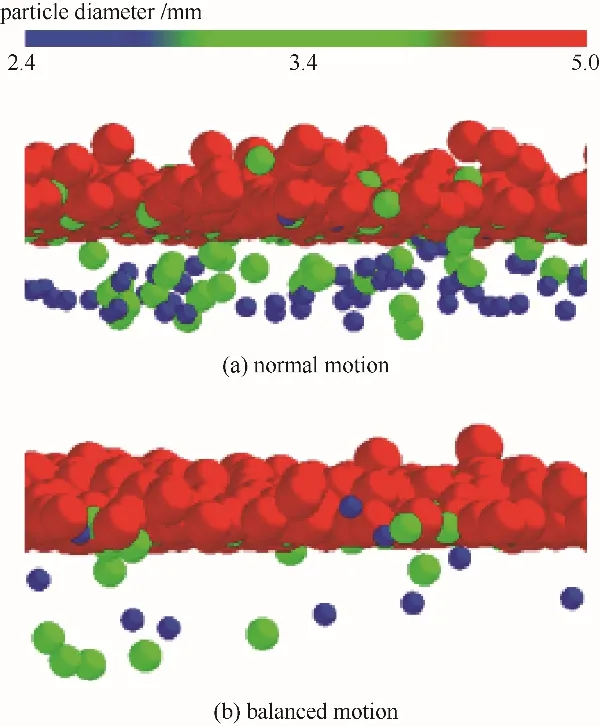
图11 两种运动的物料层分布情况（工况3，t=1.40 s）Fig.11 Distribution of material layers under two kinds of motions(working condition 3,t=1.40 s)

当颗粒物料全部生成并落至筛面后（t≥1.30 s），常规运动下物料在筛面中部的局部输送速度基本大于整体输送速度，最大输送速度达到了137 rad·s-1，且变化规律不稳定。这种情况使得物料较快地从筛面中部向周边扩散，其在筛面中部的颗粒含量远小于其在筛箱周边的颗粒含量[图6(b)～(d)]。物料的整体输送速度主要表现为颗粒物料集中在筛箱周边的旋转输送运动，输送角速度大致为78 rad·s-1，其整体输送速度的变化范围不大(图9)。

当颗粒物料全部生成并落至筛面后（t≥1.30 s），均衡运动下物料在筛面中部的局部输送速度小于整体输送速度。随着物料在筛面上径向位移的增加，筛面上对应点的圆周振幅逐渐增大，使得物料在筛面上的局部输送速度也逐渐增大。由于筛面边缘点的圆周振幅较大，当颗粒物料旋转扩散至筛箱周边时，旋转输送速度会明显大于整体输送速度(图10)。物料的整体输送速度变化范围为63～77 rad·s-1，局部输送速度变化范围为27～58 rad·s-1。物料沿整个筛面充分散开，保证了筛分物料粒度沿筛面分布的均匀性，降低了物料层厚度，提高了物料筛分的效率。

3.2 固相筛分效率

筛分效率指实际筛下物的质量与入料中小于筛孔粒级的所有细粒物料质量的比值，本文采用量效率公式[37]计算筛分效率，其表达式为：

两种运动下旋振筛的固相筛分效率及小粒度颗粒透筛率计算结果分别如表7和表8所示。

在振幅相似、频率相同的条件下，均衡运动旋振筛的固相筛分效率更高，其优势主要体现在对粒径比在d/a=0.7～1.0之间颗粒透筛效果的处理能力上。对于所有粒径比在d/a=0.5～0.7之间的颗粒，两种运动的颗粒透筛率基本都可以达到97%以上，只有极少部分颗粒不能透筛而在筛面振动作用和颗粒碰撞作用下随粒群一起运移排出。

透筛速度表征着颗粒的透筛概率，决定了筛分效率。取同一时刻筛面上所有某类型颗粒透筛速度的平均值作为该类型颗粒物料在该时刻的透筛速度。图13为颗粒物料透筛速度变化曲线（d/a=0.5～0.7），其中常规运动颗粒透筛速度的平均波动范围为-0.05～0.04 m·s-1，均衡运动颗粒透筛速度的平均波动范围为-0.09～0.12 m·s-1。均衡运动无论是颗粒透筛速度的最大值还是其平均波动范围均要优于常规运动，表明均衡运动颗粒透筛概率更高。

图12 颗粒物料输送速度变化曲线（工况3）Fig.12 Change curve of conveying velocity of granular materials(working condition 3)

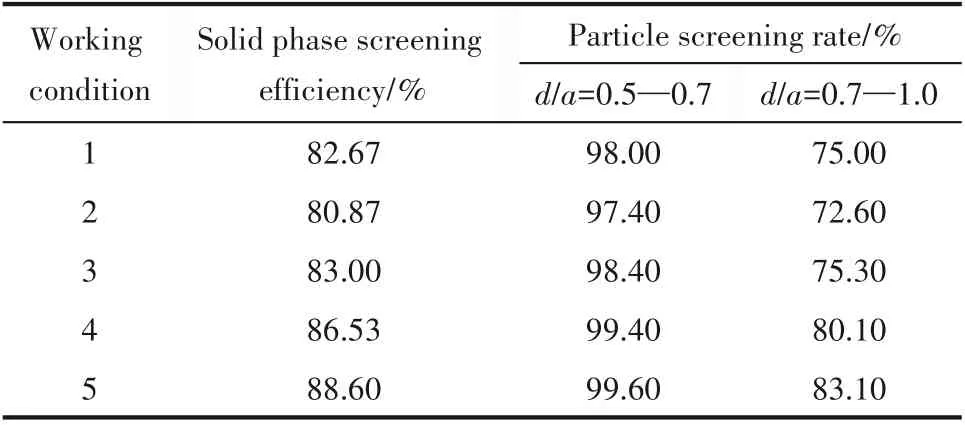
表7 常规运动旋振筛的固相筛分效率及颗粒透筛率Table 7 Solid phase screening efficiency and particle screening rate of rotary vibrating screen under normal motion

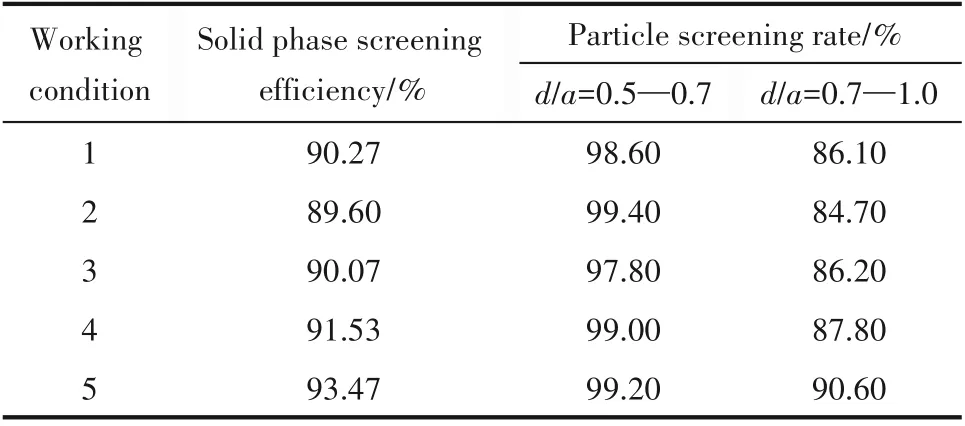
表8 均衡运动旋振筛的固相筛分效率及颗粒透筛率Table 8 Solid phase screening efficiency and particle screening rate of rotary vibrating screen under balanced motion

同时颗粒的透筛速度是正负交替变化的，当颗粒透筛速度为负数时，颗粒背离筛面向上运动。即颗粒的透筛并不是一个连续过程，粒群的运动交替发生于颗粒物料接触透筛和脱离筛面两种情况之间。为提高颗粒透筛概率，应适当增大颗粒的透筛速度。

图14为颗粒物料透筛速度变化曲线（d/a=0.7～1.0），其中常规运动颗粒透筛速度的平均波动范围为-0.01～0.01 m·s-1，均衡运动颗粒透筛速度的平均波动范围为-0.08～0.10 m·s-1。常规运动无论是颗粒透筛速度的最大值还是其平均波动范围均相对均衡运动较小，存在着颗粒透筛相对困难的问题。

以垂直筛面向上为正方向，筛面上物料以粒径比在d/a=1.0～3.0之间颗粒为主，其垂直方向速度变化主要表现为粒径比在d/a=1.0～3.0之间颗粒垂直方向的运动变化趋势，如图15所示。常规运动颗粒物料垂直方向速度的平均波动范围为-0.01～0.01 m·s-1，均衡运动颗粒物料垂直方向速度的平均波动范围为-0.10～0.09 m·s-1。均衡运动下大粒度颗粒（d/a=1.0～3.0）更容易被抛起，粒群会变得更松散和分层，物料层相对更薄，也更利于小粒度颗粒的透筛。

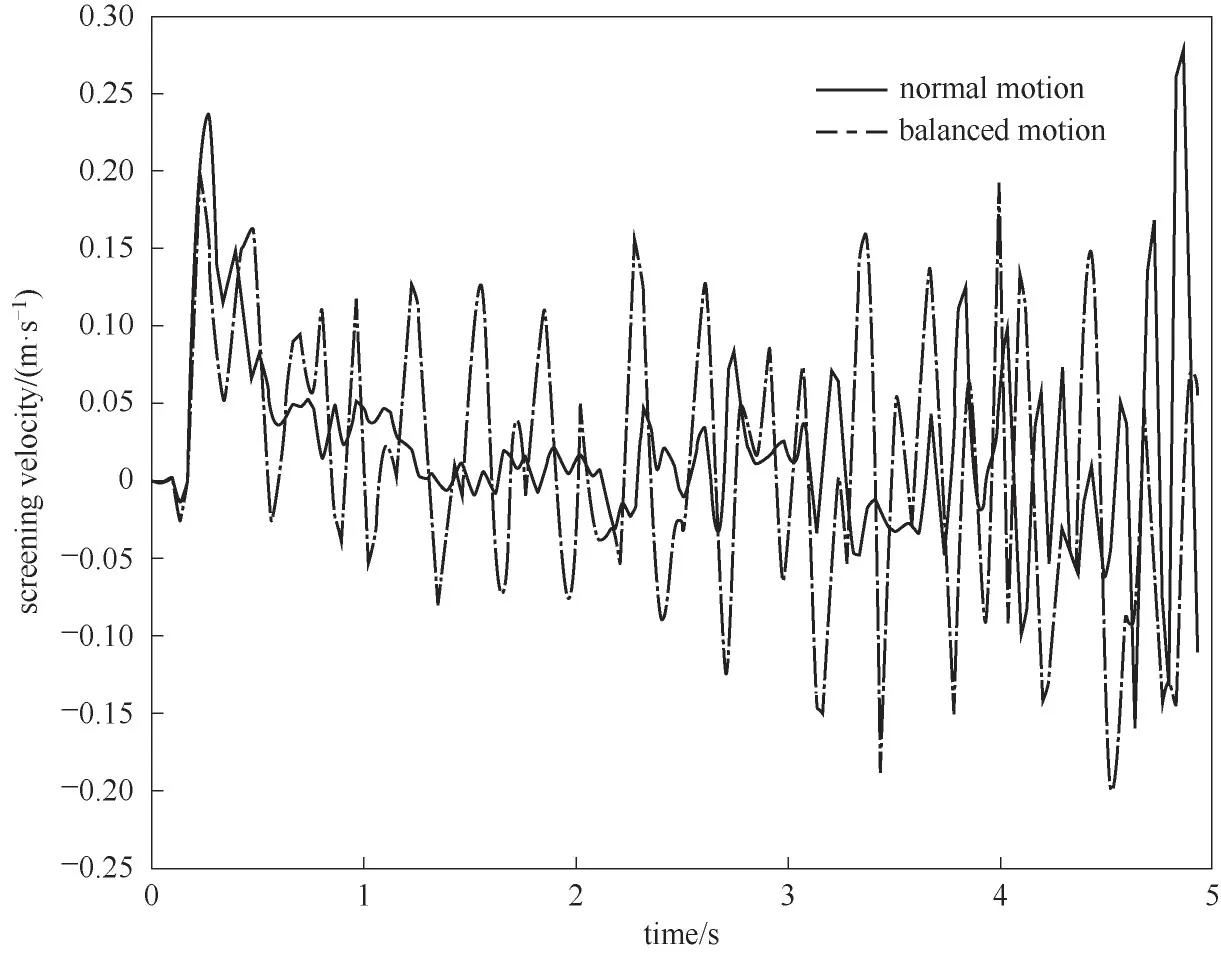
图13 颗粒物料透筛速度变化曲线（工况3，d/a=0.5～0.7）Fig.13 Change curve of screening velocity of granular materials(working condition 3,d/a=0.5—0.7)

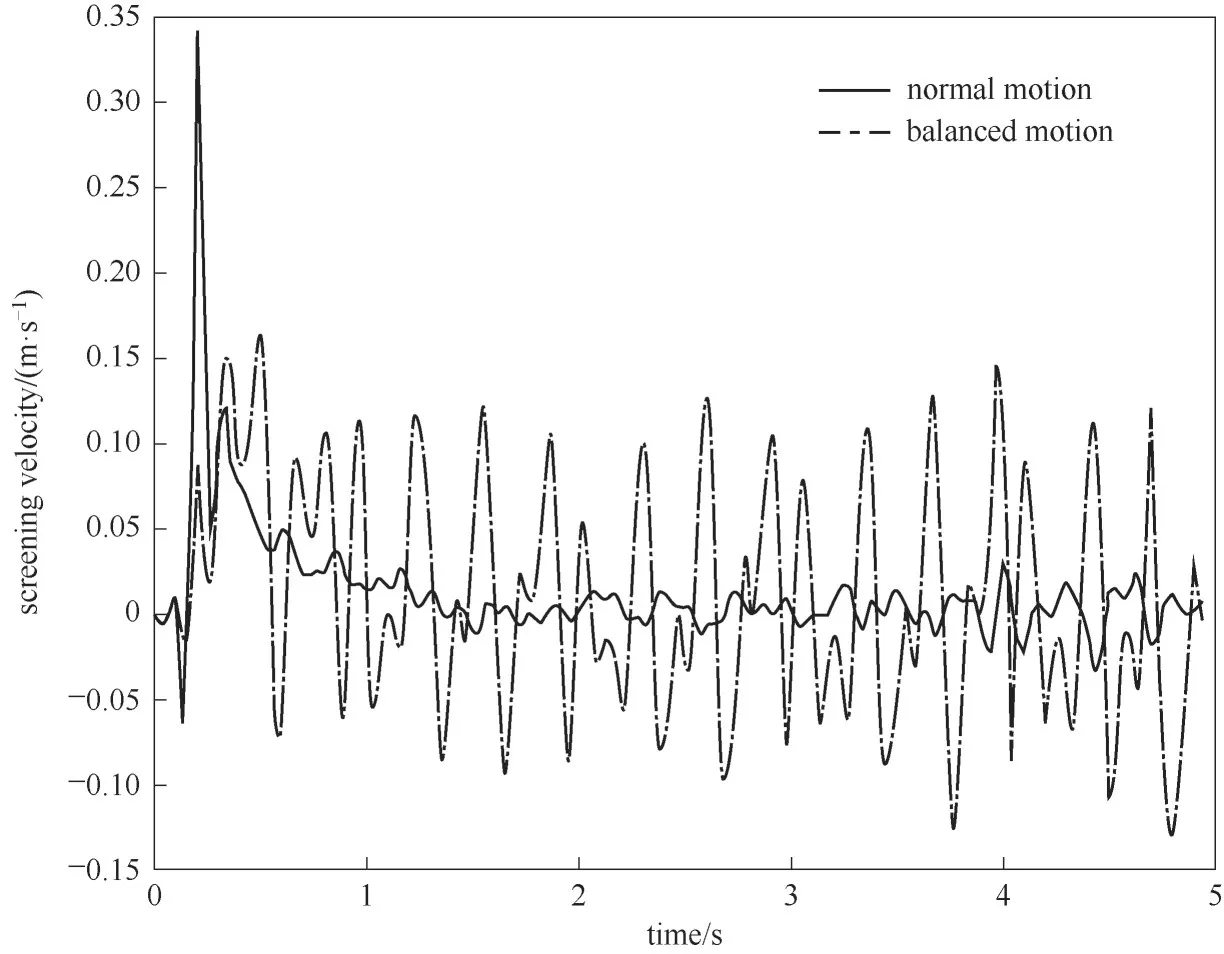
图14 颗粒物料透筛速度变化曲线（工况3，d/a=0.7～1.0）Fig.14 Change curve of screening velocity of granular materials(working condition 3,d/a=0.7—1.0)

在工况3工作参数及其他几何参数不变的情况下，分别改变旋振筛DEM仿真几何模型的筛孔孔径为6 mm和8 mm，则两种运动下旋振筛的固相筛分效率及小粒度颗粒透筛率计算结果如表9所示。均衡运动由于筛面上均匀分布的垂直振幅及物料在旋转扩散过程中相对较薄的物料层，使小粒度颗粒落至筛面中部时就具有较大且较稳定的透筛速度波动范围，有利于提高颗粒透筛率及均匀度，可较好解决颗粒粒径与筛孔孔径比在0.7～1.0之间时颗粒透筛相对困难的问题。

4结 论

本文提出了一种均衡运动原理的旋振筛，通过DEM数值模拟，在振幅相似、频率相同的条件下，从筛分效率的角度直观比较了旋振筛在常规运动和均衡运动下的筛面物料运动规律、颗粒粒度分布情况、固相筛分效率及颗粒运动速度，主要结论如下。

（1）均衡运动下，物料以螺旋线轨迹从筛面中部向周边旋转扩散，其物料层较薄，具有较好的均匀性。

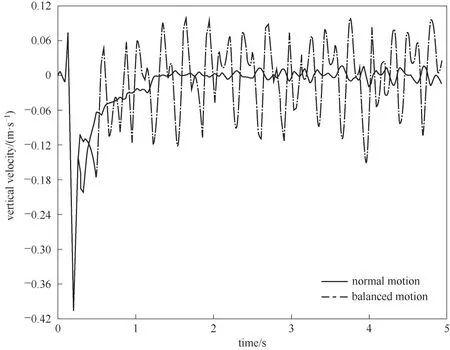
图15 筛面上颗粒物料垂直方向速度变化曲线（工况3）Fig.15 Change curve of vertical velocity of granular materials on the screen surface(working condition 3)

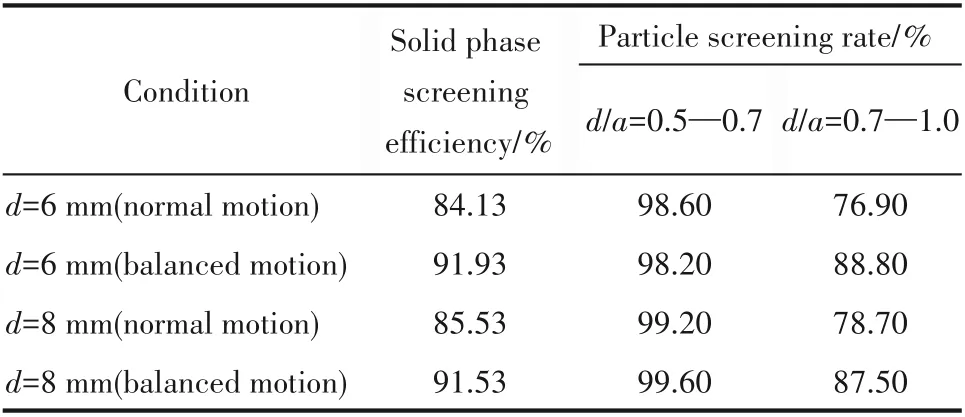
表9 不同筛孔孔径下旋振筛的固相筛分效率及颗粒透筛率（工况3）Table 9 Solid phase screening efficiency and particle screening rate of rotary vibrating screen under different aperture size（working condition 3）

（2）在振幅相似、频率相同的条件下，均衡运动能有效提高旋振筛的固相筛分效率，可较好解决颗粒粒径与筛孔孔径比在0.7～1.0之间时颗粒透筛相对困难的问题。

（3）均衡运动下，物料在筛面中部的局部输送速度小于整体输送速度。随着物料在筛面上径向位移的增加，局部输送速度也逐渐增大。同时无论是小粒度颗粒透筛速度的最大值还是其平均波动范围也均要优于常规运动，有利于提高颗粒透筛率及均匀度。

符号说明

A——质心圆平动幅值，mm

Axy——振动体质心偏离主轴线的距离，mm

Az——振动体的垂直振幅，mm

a——筛孔孔径，mm

c——振动体绕质心水平轴转动方向上的阻尼系数，N·m·rad-1

D——筛面上点的定义域

d——颗粒粒径，mm

J——振动体绕质心水平轴的转动惯量，kg·m2

Jz——激振轴绕自身轴线的转动惯量，kg·m2

k——弹簧水平方向总刚度，N·m-1

l1——上下偏心块间的垂直距离，m

l2——上偏心块与振动体质心间的垂直距离，m

M——振动体总质量，kg

m0——单个偏心块质量，kg

Ni——第i种颗粒的入料总数

n——筛下颗粒数量

ni——第i种颗粒的透筛数量

R——筛面上任一点相对筛面中心的半径值，mm

r——偏心距，m

t——振动时间，s

x——振动体沿x方向的位移，mm

x0——筛面上任一点的横坐标，mm

y——振动体沿y方向的位移，mm

y0——筛面上任一点的纵坐标，mm

z——振动体沿z方向的位移，mm

z0——筛面上任一点的竖坐标，mm

α——下偏心块超前上偏心块的相位角，rad

δ——主矢超前主矩的相位角，rad

ε——第i种颗粒的透筛率，%

η——筛分效率，%

θ——摆动角位移幅值，rad

θz——振动体对主轴线方向的振动幅角，rad

κ——筛上物中小于筛孔粒级的细粒含量，%

λ——筛面上任一点的圆周振幅，mm

λz——筛面上任一点的垂直振幅，mm

λˉ——整个筛面的平均圆周振幅，mm

λˉz——整个筛面的平均垂直振幅，mm

μ——入料中小于筛孔粒级的细粒含量，%

σ——积分区域圆域极角，rad

φ1，φ2——分别为振动体沿主轴线方向作垂直振动和绕主轴线方向作往复回转振动对应的初相位，rad

ψx，ψy——分别为振动体绕质心向x、y轴摆动的角位移，rad

ψz——振动体绕主轴线方向作往复回转的角位移，rad

ω——旋转角速度，rad·s-1