区域气候模式CWRF对我国极端温度时空变化的模拟评估

刘旗洋 乔枫雪 ,3 朱奕婷 梁信忠 柳雨佳 张焓 王瑞

1 华东师范大学地理信息科学教育部重点实验室，上海 200241

2 华东师范大学地理科学学院，上海 200241

3 崇明生态研究所，上海 200062

4 南京信息工程大学大气科学学院，南京 210044

5 马里兰大学帕克分校大气与海洋科学系 美国

6 马里兰大学地球系统科学跨学科中心 美国

7 上海中心气象台，上海 200030

1 引言

政府间气候变化专门委员会第五次评估报告（AR5）指出，全球平均陆地和海洋表面温度的线性趋势计算结果表明，在1880～2012年期间温度升 高 了 0.85°C（0.65～ 1.06°C）（IPCC,2013），全球气候正经历以变暖为主要特征的变化。《中国气候变化蓝皮书（2019）》指出，1951～2018年中国年平均气温上升速率为0.24°C/10 a，升温率明显高于同期全球平均水平，其中1980年以来的升温尤为显著（中国气象局气候变化中心,2019）。全球变暖不仅体现在平均气温的升高，更重要的是极端气候事件的变化。极端气候事件具有突发性、难预测性和强破坏性的特点，其中区域性的极端高温或低温事件直接影响农业生产和人体健康，对生态环境和社会经济可持续发展构成巨大的挑战，从而引发人们更多的关注。2000年以来，我国区域性极端温度事件频发，且影响范围大、持续时间长，例如我国2008年南方持续性低温雨雪事件和2013年华东异常罕见的连续高温事件，造成了巨大的经济损失（马宁等,2011; 邹海波等,2015）。

已有大量研究基于观测数据，利用不同的极端气候指数，分析我国极端温度阈值或事件的变化趋势和时空分布，这些研究显示我国极端温度指数的变化趋势对气候变化的响应较为复杂，存在显著的区域差异（翟盘茂和潘晓华,2003; 马柱国等,2003;周雅清和任国玉,2010; You et al.,2011）。自 1960年以来，我国整体上极端温度指数表现为冷指数的变暖幅度大于暖指数，夜指数的变暖幅度大于昼指数（杨萍等,2010; 王琼等,2013; 王晓利和侯西勇,2017），极端低温事件的频次、强度和范围呈减弱趋势（王晓娟等,2012），但冷日持续指数（CSDI）的变化趋势不显著；各极端温度指数在南方地区的变化幅度小于北方，且随着海拔的升高变化幅度变大（张大任等,2019）。极端最高/最低温度的升温幅度在东北地区最显著，暖日和暖夜在西南地区逐步增加，高温日数在中部地区显著增加；北方的冷昼和冷夜指数大幅减少而暖昼和暖夜指数显著增加，中部地区的各极端温度指数年际变化较不显著（Zhou and Ren,2011; 肖冰霜等,2016）；青藏高原地区的最低温度极小值的上升速率最快，最高温度极大值的上升速率最慢，存在显著的冷暖不对称性（周玉科等,2017）。我国极端低温和极端高温的年代际变化趋势较为一致，但具有明显的阶段性特征，不同区域极端气温指数主周期介于2～8年，无显著的年代际振荡周期变化，不同区域的极端温度指标在1986～2015年的变化趋势相对1956～1985年更为显著，突变集中发生在1980年代和1990年代期间（Zhou and Ren,2011; 王晓利和侯西勇,2017; 张大任等,2019）。因此，本研究着眼变化趋势显著的1980～2015年，较为细致的研究我国8个气候区域基于阈值的极端温度指数的变化特征。

全球气候模式（Global Climate System，GCM）和降尺度的区域气候模式（Regional Climate System，RCM）是研究气候过程和气候变化机理的重要方式，为了准确可靠地预测未来极端温度的变化，需要对数值模式的模拟结果进行评估。已有大量的研究对耦合模式比较计划（Coupled Model Intercomparison Project，CMIP）的多模式结果进行温度模拟评估和未来变化的预估（Jiang et al.,2015）。王冀等（2008）指出7个全球海气耦合模式模拟平均结果优于单个模式，但对我国平均霜冻、暖夜和热浪的空间分布都存在系统性高估；姚遥等（2012）评估了8个CMIP5 耦合模式对我国极端气温的模拟效果，表明模式集合能够模拟极端温度指数的平均状态和年际变化特征，但对气候极值的模拟存在较大的不确定性，高温热浪指数的模拟偏差超过8%，暖指标的年际趋势模拟优于冷指标。GCM对大尺度环流特征的模拟较好，但受制于分辨率较低，无法细致地描述天气气候过程，对极端温度的区域及年际变化特征的模拟及预测能力有限，需要进行多模式集合和偏差订正对输出结果进行修正（Seo and Ok,2013; 高谦,2017）。经过动力降尺度后的 RCM 具有较高的分辨率，对于刻画我国区域性的气温、降水的分布及变化有一定优势，能较好地模拟到四川盆地的高值中心，而且对青藏高原平均气温的低估得到明显的改善（Gao et al.,2011,2013; Liu et al.,2013; Wang et al.,2015; Yu et al.,2015）。其中，RegCM（Regional Climate Modeling system）系列模式在我国极端温度模拟和变化预估上有着广泛的应用（Feng et al.,2011; Gao et al.,2012,2017; 高学杰等,2012; Xu et al.,2013; Ji and Kang,2015）。李东欢等（2017）指出RegCM3对日最高气温极大值模拟偏差表现为西部2～4°C的冷偏差和长江流域1～3°C的暖偏差；日最低气温极小值模拟在大部分地区存在3°C的冷偏差，在青藏高原达到5°C以上；Kong et al.（2019）比较了 WRF 和 RegCM4对我国极端温度的模拟结果，WRF对极端温度指数的年际趋势模拟较好，RegCM4对我国极端气温的平均气候态模拟较好，但低估了青藏高原极端高温的年际变化的增暖趋势；高谦（2017）指出经过动力降尺度的LMDZ4模式对我国极端温度的平均模拟偏差减少且空间相关系数提高，一定程度上体现了青藏高原、四川盆地等复杂地形的极值中心；张玉静（2017）指出 PRECIS（Providing Regional Climates for Impacts Studies）模式能够模拟极端温度阈值的空间分布特征，但对西北、东北和四川盆地等的高温阈值模拟高估2°C，对青藏高原南部和东部的高温阈值模拟低估超过5°C，对我国大部分的低温阈值存在普遍的低估。虽然RCM模式模拟分辨率有所提升，但对青藏高原等高复杂地形区域的温度模拟仍存在较大的挑战，除了模式物理过程参数化的不足以外，也与气象观测站稀疏且海拔较低有关（Yu et al.,2015）。

本研究着重评估基于中国本地化季节气候预测的区域气候模式 CWRF（regional Climate–Weather Research and Forecasting model）（Liang et al.,2019），该模式引入了较完备的物理过程参数化方案，同时增加了对温度模拟影响最为直接的云—气溶胶—辐射（Cloud–Aerosol–Radiation，CAR）相互作用的耦合模块（刘冠州和梁信忠,2017）。已有研究表明CWRF具有模拟东亚季风区大气环流与气候特征的能力，对中国地区季节平均降水、夏季极端降水的模拟能力较好（刘术艳等,2008; 董晓云等,2019）。Liang et al.(2019)目前只初步分析了控制方案对平均温度与日最高、最低温度的季节模拟偏差，尚未进行基于不同极端温度指标的区域分布及变化特征的模拟评估。因此，本文将基于1980～2015年的全国气温观测数据和模式控制版本的连续积分结果，从空间分布、概率分布、年际变率和年际趋势方面，系统地评估区域气候模式CWRF对我国不同区域的极端温度指数的模拟能力及偏差所在，为完善模式的物理过程、提升模式模拟预测能力提供依据。

2 数据和方法

2.1 模式介绍及模拟数据

本研究使用的区域气候模式CWRF自2001年研发以来，结合卫星遥感数据，考虑人类活动、植被等动态演变，优化30 km水平分辨率的下垫面及侧边界数据（Liang et al.,2019）；针对关键物理过程，在WRF模式的基础上，集成了多种参数化方案（刘冠州和梁信忠，2017）。CWRF模式的模拟区域中心点位于（35.18°N，118°E），采用地形跟随坐标系，垂直方向包括36层；水平网格采用Lambert投影的232（纬向）×172（经向）个格点的30 km的等距网格。海温数据采用欧洲中心再分析资料ECMWF-Interim日平均海表温度（1979～1980年）和美国国家海洋大气管理局NOAA的最优插值日海表温度（OISST，1981～2015年，0.25°）（Reynolds et al.,2007; Banzon et al.,2016）。经过多次敏感性试验和验证，确定了基于中国地区气候模拟预测的控制实验方案，包括ECP对流方案（Qiao and Liang,2016,2017）、GSFCGCE 微物理方案（Tao et al.,2003）、GSFCLXZ 辐射方案（Chou et al.,2001）、CAM3 边界层方案（Rontu,2006）、CSSP 陆面方案（Liang et al.,2005）和XRL 气溶胶方案（Liang et al.,2004）。关于该模式在中国地区的相关改进及具体物理方案的设置详见 Liang et al.(2019)。研究使用 ERA-Interim（Dee et al.,2011）作为初始场和边界场驱动CWRF模式，从1979年11月1日连续积分至2015年12月31日的3 h模拟数据，前两个月为模式的启动时段，着重评估1980年1月1日至2015年12月31日的温度数据。

2.2 观测资料和极端温度指数

历史气温观测数据来自中国地面气象台站观测的格点化逐日平均气温、日最高气温、日最低气温观测资料（CN05.1），水平分辨率为0.25°（纬度）×0.25°（经度），其原始数据来自我国2000多个站点的均一化长序列气温数据，能够较真实地反映历史极端温度的趋势和变率（Xu et al.,2009;吴佳和高学杰,2013）。本文选取的时间范围为1980～2015年的日资料，为了便于与模式的比较，利用双线性插值将格点观测数据插值到与模式对应的等间距30 km的Lambert投影格点。由于我国南北跨度大，气候、地形和下垫面因子复杂多变，参照了 Hui et al.（2015）、Yu et al.（2015）、Zhou et al.（2016）等的研究分区，本文划分8个区域对极端温度的区域差异特征进行细致的研究（图1），包括东北、华北、华东、华南、西南、青藏高原、西北、西北东部。

合适的极端温度指数需要同时具有对气候变化敏感且稳定性高的特点，对于研究结论的可靠性具有重要作用。气候变化检测和指数专家组（ETCCDI）和“欧洲地区极端事件统计和区域动力降尺度”（STARDEX）提出的极端气候指数，是国际上常用的极端气候评价指标，能够定量描述极端温度事件的变化，具有低噪声和强指示性的优势（Alexander et al.,2006; 胡彩虹等,2013）。本文参照陈正洪等（2010）提出的极端温度指数计算方法，首先是将1981～2010年作为气候基准期，得到某一天及其前后两天（共计5天）在30年气候基准期内共计150天的日最高、最低气温数据，对样本取90%或10%的分位值作为阈值，并以超过90%或低于10%分位值的气温作为极端温度，相比采用绝对阈值得到的极端气候指数，该方法能同时体现我国区域性和季节性的极端温度差异。本文选用暖昼指数（TX90）、冷昼指数（TX10）、暖夜指数（TN90）、冷夜指数（TN10）、暖日持续指数（WSDI）和冷日持续指数（CSDI）来研究中国极端温度的变化（表1）。

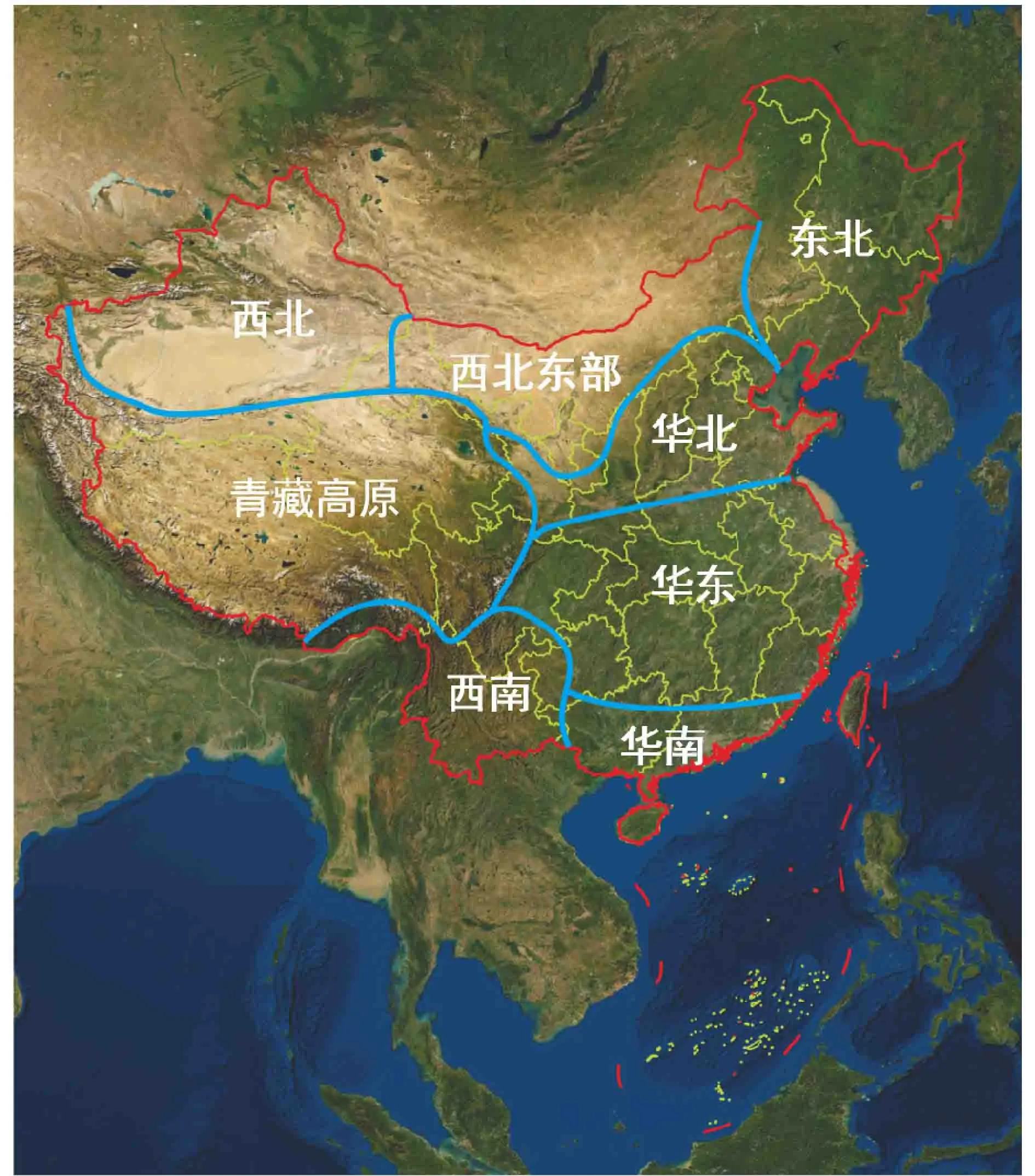
图1 中国 8 个子区域的地理位置划分Fig.1 Geographic locations of eight subregions in China

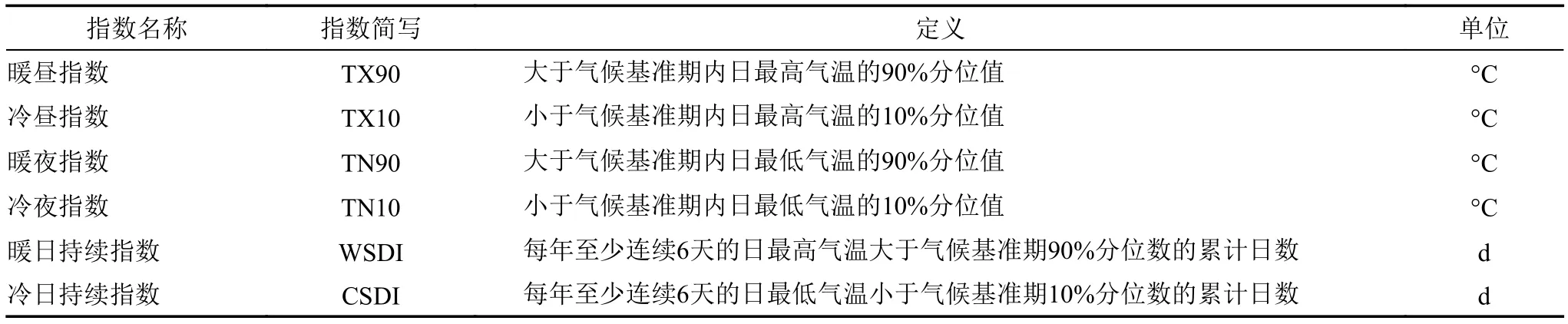
表1 极端温度指数的定义Table 1 Definition of extreme temperature indices used in this study

2.3 统计分析方法

（1）泰勒图

泰勒图（Taylor,2001）可以全面直观地比较模拟的极端温度与观测的极端温度的一致性，它是由模拟场与观测场的空间相关系数、相对标准差及其中心化的均方根误差组成的极坐标图，中心化的均方根误差越接近0，空间相关系数和相对标准差越接近1，模式模拟能力越好。本文利用泰勒图综合评估CWRF模式对不同区域极端温度指数的模拟效果。

（2）概率分布模拟

为了衡量两个分布之间的相似性，常用的方法有 KL散度（Kullback-Leibler divergence）和 JS散度（Jensen-Shannon divergence），常用作模型的拟合损失评价指标。JS散度的计算基于KL散度做了改进，解决了KL散度非对称的问题。对于两个概率分布p(x)和q(x)，JS散度计算公式如下：

其中，

因此，JS散度是对称且有界的，其取值在0到1之间。利用上式，本文将极端温度指数（TX90、TN90、TX10、TN10）的观测和模拟概率分布分别作为P(x)和Q(x)，以此来定量评估CWRF对不同区域的极端温度分布特征的模拟效果。JS散度值越小，则表示观测和模拟的概率分布的越接近，模拟效果越好。

（3）年际变化趋势分析

常用的趋势分析方法包括最小二乘法线性回归估计，该方法对离群值敏感且要求数据满足正态分布，而Theil–Sen 的趋势估计和Mann–Kendall（MK）检验要求时序数据不具有自相关性。张嘉仪和钱诚（2020）指出高温热浪数据大多数不服从正态分布且存在较强自相关，传统的趋势分析方法存在一定缺陷。考虑到极端温度变化具有不连续性和突变性的特点，波动较大且离群点较多，Yue and Wang（2002）基于MK趋势分析做了改进，对时间序列进行了预白化处理，不易受离群值影响且无需满足正态分布，对于极端温度的年际趋势估计结果更具稳定性和可靠性，因此本研究主要采用改进的MK趋势分析方法，对我国不同区域极端温度指数的年际变化趋势进行分析。

3 区域极端温度指数的时空分布特征及变化趋势的模拟评估

3.1 年极端冷、暖指数的空间分布特征

图2比较1980～2015年观测和CWRF模拟的TX90、TX10、TN90、TN10的年平均空间分布特征。这4个指数着重体现日、夜的高温和低温的强度特征。首先从观测中可看出，暖指数（暖昼、暖夜）、冷指数（冷昼、冷夜）具有显著的不同的区域型分布特征。其中，暖指数（TX90、TN90）的极大值区均位于华南地区（年均阈值分别是34°C、28°C以上），高值区域向北扩展经过华东华北，分别向东、西两侧伸展，在西北内陆以及东北三省暖指数温度均较高；暖指数的显著低值区域均位于青藏高原地区。然而，冷指数（TX10、TN10）的高值区域集中分布在华南及华东（年均阈值分别是23°C、13°C以上）以及西北地区天山以南地区（年均阈值分别是18°C、5°C以上）；冷指数的低值区域主要位于高原以北—西北东部—东北偏北一线，其中冷昼TX10、冷夜TN10在高原北部、东北北部温度最低（年均阈值分别在0°C、−15°C以下）。

图2 1980～2015年平均 TX90、TX10、TN90、TN10 指数的观测（OBS）、模拟（CWRF）、模式偏差（BIAS）和均方根误差（RMSE）的空间分布Fig.2 Spatial distributions of annual mean extreme temperatures indices (TX90,TX10,TN90,and TN10) from 1980 to 2015 from observation(OBS),CWRF simulation,and model biases (BIAS) as well as the root mean square errors (RMSE)

从年空间分布的CWRF模式模拟来看，模式基本再现了观测的暖、冷指数总体的空间分布特征。基于模拟偏差的空间分布图，可以发现：（1）模式对暖指数（暖昼、暖夜）的温度模拟存在系统性的低估，青藏高原比较显著，在全国大部分区域均有2°C左右的冷偏差；其中暖昼在华南、西南地区的低估偏多（局地超过−4°C）；（2）模式对冷指数（冷昼、冷夜）的温度模拟偏差存在区域性的差异，在青藏高原南侧均存在系统性的低估，但高估华东及华北地区的冷昼温度（局地超过3°C），以及西北—东北地区冷夜温度（局地超过4°C）；由此可见，CWRF模式对1980～2015年的暖指标温度较高的地区存在系统性低估，冷指标温度较低的地区存在系统性的高估，说明模式对这些地区的日最高温度的模拟偏低，对日最低温度的模拟偏高，但对青藏高原地区的日极值温度（高温、低温）存在系统性的低估。对于高原以外地区极端温度的变率模拟偏低的问题，原因可能比较复杂，Liang et al.（2019）指出模式对我国中部及南部地区夏季平均温度的年际变化特征的模拟性能有限，并指出了该区域存在强的对流活动与复杂的海陆气相互作用。因此，该地区极端温度模拟的偏差，可能与大尺度环流的强迫与区域因素和物理过程之间的反馈相关，尤其需要进一步发展优化的多物理过程集合来提高模式对关键的对流—微物理—辐射以及下垫面—大气相互作用的表达。

图3为1980～2015年平均的我国暖日持续指数（WSDI）和冷日持续指数（CSDI）的空间分布特征。这两个指数与图2中的阈值强度不同，着重表征暖冷指标的持续性特征，能够反映持续性极端温度事件的区域性分布特征。由观测可知：1980～2015我国年平均WSDI在西北、青藏高原和西南地区偏高，其中部分地区长达10 d以上；CSDI在西南南部、华南南部、东北北部和西北地区较高，长达8 d以上；整体而言，WSDI的持续性比CSDI更为明显。

CWRF模式对我国大部分地区暖日和冷日持续指数的模拟偏差较小，存在显著优势，尤其对西北地区天山一侧、青藏高原南部、西南云贵的持续高温事件，以及我国东部地区包括华东、华南以及东北地区的持续低温事件模拟误差普遍较小；WSDI的偏差范围和偏差幅度都小于CSDI，模式对WSDI模拟优于对CSDI模拟。然而，模式仍存在的问题是对华东中部地区的WSDI、西北地区的CSDI存在系统性的高估（年均3 d和5 d以上）。

图3 1980～2015年平均WSDI指数（第一列）、CSDI指数（第二列）的（a、b）观测、（c、d）模拟、（e、f）模式偏差的空间分布Fig.3 Spatial distributions of annual mean WSDI (warm spell duration indicator,first column) and CSDI (cold spell duration indicator first column,second column) from 1980 to 2015 from (a,b) observation,(c,d) CWRF simulation,and (e,f) model biases

3.2 区域模拟误差统计特征评估

图4为 1980～2015年 CWRF模拟的 TX90、TX10、TN90、TN10在8个不同区域的平均偏差盒须图。结果显示，暖指数的模拟在8个区域均为系统性的冷偏差，但偏差幅度存在区域差异。其中，暖昼TX90在西南和青藏高原地区的冷偏差较大（5°C以上），其余地区冷偏差约2～5°C；暖夜TN90相比于TX90，冷偏差幅度较小，在西南和青藏高原地区约偏低3～4°C；冷指数的模拟在青藏高原地区均为冷偏差，其余地区均以暖偏差为主；其中青藏高原地区，冷昼TX10和冷夜TN10的温度模拟分别偏低 2°C和 1°C；除此之外，冷昼TX10在西南地区出现弱的冷偏差；对于西北—西北东部—东北地区，冷夜TN10的暖偏差超过2°C，普遍高于冷昼TX10的偏差幅度。该统计结果与前面模拟偏差的空间分布特征一致，表明模式对青藏高原地区的暖、冷指数的模拟均偏低；然而，对其他大部分地区，模式系统性低估暖指数的温度，其中对暖日的低估幅度较大；模式系统性高估北方地区冷指数的温度，尤其冷夜的高估幅度较大。

图5是 CWRF模拟的 TX90、TN90、TX10、TN10在8个不同区域的极端温度指数的JS散度，用于衡量极端温度的观测概率分布与模拟概率分布之间的差异，其数值越接近于0，说明两个分布重合度越高，其数值越接近于1，则说明两个分布重合度越低。结果显示：（1）模式模拟的暖指标（暖昼TX90、暖夜TN90）的概率JS评分均在南部地区（华南、西南、青藏高原）偏高，模拟偏差显著，对应图2中暖指标在对应区域存在显著的冷偏差；并且，模式对于暖昼TX90的JS评分普遍高于暖夜TN90，表明模式模拟的暖夜TN90的偏差相对较小，与图2中两者的区域偏差数值较一致；（2）模式模拟的冷指标（冷昼TX10、冷夜TN10）的概率JS评分与图2中的偏差分布也较为一致。其中，冷昼JS评分偏大的区域为华北和华东，对应图2中的TX10暖偏差高值区；冷夜JS评分偏大的区域为西北—西北东部—华北—东北的北部地区，对应图2中TN10暖偏差高值区；因此，模式模拟的JS评分也定量的指出，模式对暖指标模拟冷偏差较大的地区主要在南部地区（华南、西南、青藏高原），且暖昼模拟的偏差比暖夜要大；然而，模式对冷指标模拟暖偏差较大的区域分别在中部偏东（华北、华东）、北部地区（西北—西北东部—华北—东北）。

图6为 CWRF模拟的 8个不同区域 1980～2015年的年平均的 TX90、TX10、TN90、TN10指数的泰勒图。结果显示，暖、冷指标在8个区域的相关系数基本都超过0.8，表明模式对于这4个指数的区域空间分布基本特征模拟较好；标准差体现了模拟误差的波动程度，结果表明CWRF模式对北方（西北、东北）和青藏高原的极端温度模拟的标准差较大，而对南方（华南、西南和华东）的极端温度模拟的标准差较小。结合图5可知，与北方地区相比较，南方地区模拟的极端温度指数的标准差较小，说明该地区极端温度的变化阈值范围小于北方地区；同时，南方地区的JS散度较大，说明该地区模式模拟极端温度概率密度分布与观测的分布不重合度较高。二者综合分析得出，南方地区的极端温度指数概率大值区的模拟存在较大偏差，对应图7中极端温度指数，TX90，TX10，TN10在南方尤其是青藏高原、华东地区的极值温度的较大偏差。

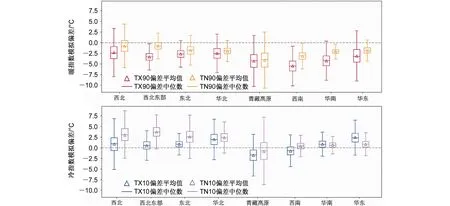
图4 1980～2015年平均的（a）TX90和TN90、（b）TX10和TN10指数在中国8个不同区域的模拟偏差盒须图Fig.4 Boxplot of model biases for annual mean (a) TX90 and TN90,(b),TX10 and TN10 indices over eight subregions in China from 1980 to 2015

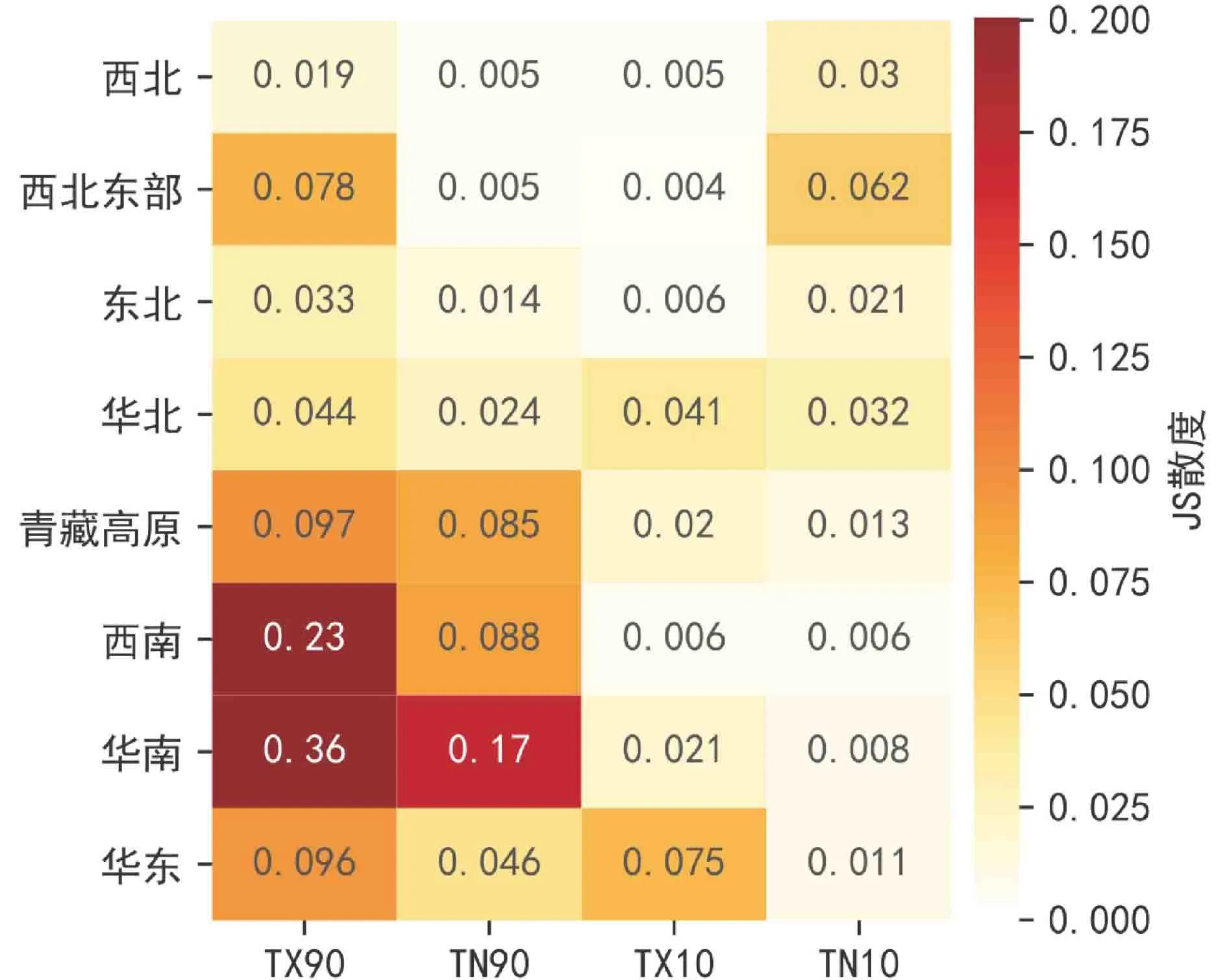
图5 CWRF模拟的中国8个区域极端温度指数的概率分布JS散度Fig.5 Jensen –Shannon divergence of CWRF simulated probability distribution of extreme temperature indices over eight subregions in China

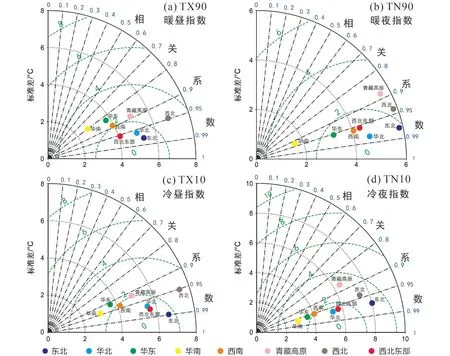
图6 CWRF 模拟的中国 8 个不同区域 1980～2015年平均（a）TX90、（b）TN90、（c）TX10、（d）TN10 指数的空间分布泰勒图Fig.6 Taylor diagrams of (a) TX90,(b) TN90,(c) TX10,and (d) TN10 indices simulated by CWRF averaged over eight regions in China from 1980 to 2015

3.3 极端温度指数的年际变率空间分布特征

极端温度指数年际变化的标准差可以反映区域极端温度波动的特征，图7为基于格点的1980～2015年观测和CWRF模拟的TX90、TX10、TN90、TN10指数的年际变化的标准差分布及其偏差、二者相关系数的空间分布。1980～2015年观测的4个极端温度指数的年际变化的共性特征是北方的年际变率的幅度明显高于南方。其中，暖指数中的TX90的年际变率在西北和东北地区显著高于TN90，而冷指数的TX10和TN10的年际变率分布近似。CWRF模式对4个极端温度指数年际变率的模拟较好，能够体现北方地区年际变率大于南方的特征；然而CWRF模拟的偏差主要位于西北、青藏高原以及东北地区，在青藏高原地区和西北地区都出现了不同程度的高估；特别的是，东北地区的TX10出现高估，而TN10出现低估。从相关系数的分布来看，模式较好地模拟了我国大部分地区1980～2015年的4个极端温度指数的年际变化特征。其中，在北方的相关系数整体高于南方，大部分地区达到0.98以上，而不同指数在南方的相关系数分布存在一定差异。西南地区的TX90、华南南部的TN90、华东地区的TX10和青藏高原的TN10相关系数较低。因此可见，对于年际变率较大的北方地区，CWRF模式能较好的模拟其大范围地区观测的极端温度指数的年际变化，但低估（高估）了在东北偏北、西北偏西地区（青藏高原、华东地区）的极端指数的年际变率幅度。

图7 1980～2015年观测（OBS）和模拟（CWRF）的TX90、TX10、TN90、TN10指数年际变化的标准差分布（第一行、第二行）、模式偏差（BIAS，第三行）和年际变化相关系数（Temporal R，第四行）的空间分布Fig.7 Spatial distributions of the interannual variances (the first line and second line) of TX90,TX10,TN90,and TN10 indices from observation(OBS) and CWRF simulation (CWRF),and their biases (the third line) as well as the interannual correlation coefficients (the fourth line)

3.4 极端温度指数的年际趋势特征的模拟评估

图8为1980～2015年观测和CWRF模拟的区域平均的极端温度指数年际变化的时间序列。观测显示极端温度指数存在较大幅度的年际波动，暖指数（TX90、TN90）在我国大部分地区都是较为显著的年际上升趋势，但冷指数（TX10、TN10）主要在北方地区（西北、东北）为年际下降趋势，而且不同暖冷指数的年际趋势的变化幅度存在区域差异。结合表2，对于暖指数，青藏高原、西南和华南地区的暖夜上升幅度超过暖昼；西北东部地区的暖昼上升趋势明显，而暖夜无显著的上升趋势；对于冷指数，青藏高原地区，冷昼出现显著的上升趋势，冷夜表现为下降趋势；西北和西北东部的冷夜下降幅度明显超过冷昼。对于持续性极端温度指数（WSDI、CSDI）的年际波动显著，CSDI总体呈下降趋势，WSDI总体呈上升趋势且更为明显。北方地区（西北、西北东部和青藏高原）的WSDI上升的趋势和CSDI下降的趋势均较大，而南方地区的WSDI和CSDI的变化趋势并不显著。CWRF模式能够很好地模拟到我国大部分地区的极端温度指数的年际变化趋势，但对于暖冷指数的强度模拟在一些区域存在较大的偏差，如南方地区，包括青藏高原、西南、华南及华东地区普遍低估的暖昼和暖夜指数，以及青藏高原低估的冷昼等。

图9进一步展示了基于改进的MK分析方法的观测和CWRF模拟的TX90、TX10、TN90、TN10指数的年际变化趋势的空间分布及模拟偏差；CWRF基本模拟到了观测中4个极端温度指数的气候变化趋势的总体分布特征及区域差异。首先，对于观测中的暖指数（TX90、TN90），我国大部分地区表现出增暖趋势。其中，模式模拟到暖昼TX90在西北、东北和四川盆地的显著增暖（局地超过1°C/10 a），在华东和华南沿海的弱增暖，在青藏高原地区弱变冷的趋势特征；然而在青藏高原和华东地区的趋势模拟出现负偏差。同时，模式较好地模拟到了观测中暖夜TN90在全国大部分地区显著增暖的趋势特征，但模式高估了青藏高原的变暖趋势，低估了华东地区的变暖趋势。其次，观测中的冷指数（TX10、TN10）在北方地区普遍表现为显著变冷的趋势（Xu et al.,2020），尤其是 TN10 变冷幅度和范围更广；其中，模式模拟到冷昼TX10在西北、东北显著变冷，而南方大部分地区增暖的年际趋势特征，但模式低估了在西北和西北东部的冷昼TX10变冷趋势，以及在华东地区冷昼TX10变暖的趋势。同时，模式较好地模拟到冷夜TN10在西北、西北东部和华东显著变冷，在华北、青藏高原东部、西南地区弱增暖趋势，但对于西北、西北东部和华东的变冷趋势模拟存在负偏差。

总体来说，暖指数在我国大部分地区为增暖趋势，其中暖夜TN90增暖的幅度和范围较广，而暖昼TX90主要在西北、东北和四川盆地增暖显著，模式能较好地捕捉到这些特征，但高估了青藏高原地区暖昼TX90变冷、暖夜TN90变暖的趋势，低估暖昼TX90和暖夜TN90在华东地区均增暖的趋势。然而，冷指数在我国北方地区的变冷趋势显著，其中冷夜TN10的变冷幅度和范围更广，而冷昼TX10主要在西北、东北变冷趋势显著，但在南方地区多为增暖趋势；模式能捕捉到冷指数年际趋势的空间分布特征，但低估冷昼TX10在西北、西北东部的变冷趋势，高估冷夜TN10在西北、西北东部、华东的变冷趋势。因此，CWRF模式模拟的暖指数趋势偏差主要在青藏高原、华东地区；冷指数趋势偏差主要在北方地区（西北、西北东部）和华东地区。

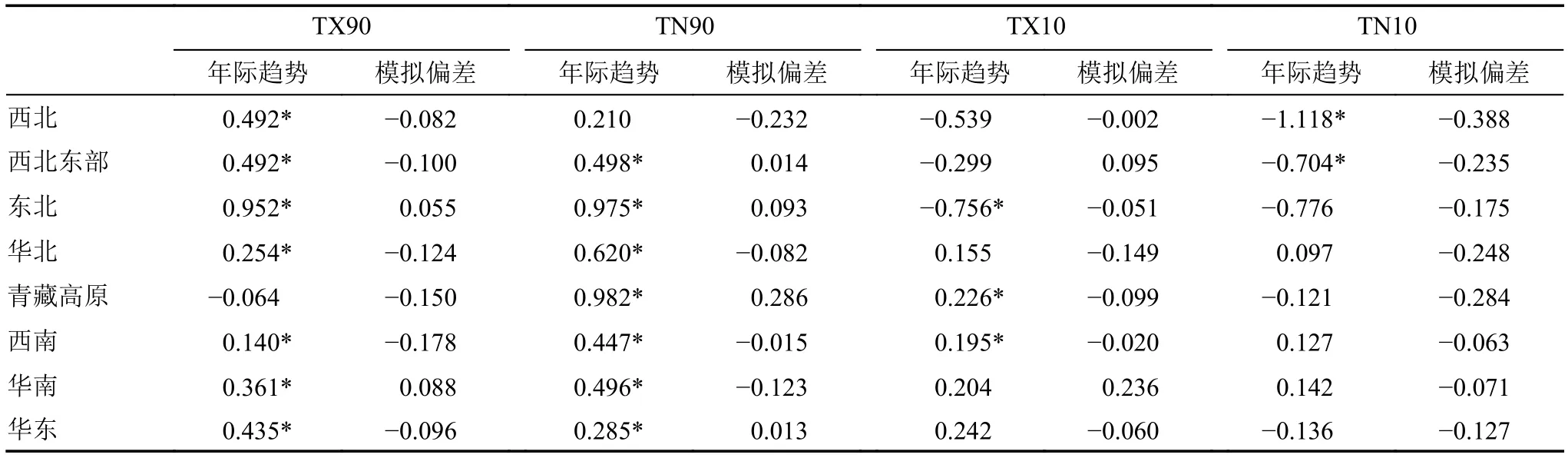
表2 1980～2015年8个不同区域的TX90、TN90、TX10、TN10指数的年际趋势及模拟偏差Table 2 Interannual trend and simulation bias of TX90,TN90,TX10,and TN10 indices over eight regions from 1980 to 2015°C (10 a)−1

4 结论及展望

本文基于1980～2015年的全国气温观测数据和区域气候模式CWRF控制版本的连续积分结果，结合暖昼指数（TX90）、暖夜指数（TN90）、冷昼指数（TX10）、冷夜指数（TN10）、暖日持续指数（WSDI）和冷日持续指数（CSDI）6个极端温度指数，利用相关系数、均方根误差、JS散度概率分布、改进的MK趋势分析等多种统计方法，从年空间分布、概率分布、年际变率、年际趋势方面，对我国东北、华北、华东、华南、西南、青藏高原、西北、西北东部8个不同气候区域的极端温度的观测特征进行细致定量的研究，系统地评估区域气候模式CWRF对1980～2015年我国不同区域的极端温度指数的模拟能力及偏差所在。得出的主要结论如下：

（1）观测的暖指数（TX90、TN90）和冷指数（TX10、TN10）的高值区均位于华南地区和西北内陆，低值区位于青藏高原和东北；CWRF模式基本再现了观测的暖冷指数的纬度地带性分布特征，但在青藏高原地区无论暖、冷指数均较观测显著偏低，存在系统性的低估；然而，模式对暖指数高值区（如华南、西南）的暖昼指数低估显著，说明该地区模拟的日最高温度偏低；同时，模式较显著高估冷指数低值区，即北方地区（西北—东北）的冷夜温度，说明该地区模拟的日最低温度偏低；

（2）观测的极端温度持续性指数（WSDI、CSDI）表明，暖事件的持续性比冷事件显著，前者大值区位于西北、青藏高原和西南地区，后者大值区位于西南南部、华南南部、东北北部和西北地区；CWRF模式对我国大部分地区持续性指数的模拟偏差小于3天，尤其对西北地区天山一侧、青藏高原南部、西南云贵的持续高温事件，以及我国东部地区包括华东、华南以及东北地区的持续低温事件模拟误差普遍较小；然而，模式仍存在的问题是对华东中部地区的暖日持续指数、西北地区的冷日持续指数存在高估；

（3）观测的极端温度指数在北方的年际变率的幅度明显高于南方，暖指数中的暖昼TX90的年际变率在北部地区显著高于暖夜TN90，而冷指数的冷昼TX10和冷夜TN10的年际变率分布近似。CWRF模式较好地模拟到4个极端温度指数在北方地区年际变率大于南方地区的特征，且对北方地区的极端温度的变化模拟更有优势，相关系数整体高于南方。然而，CWRF模拟的偏差主要位于西北、青藏高原以及东北地区，在前两个地区均为不同程度的高估，但高估东北地区的冷昼指数，低估冷夜指数；

（4）模式能够较好地模拟到暖指数在我国大部分地区的增暖趋势，以及冷指数在我国北方地区显著的变冷趋势以及冷昼指数在南方地区的增暖趋势。然而，模式高估青藏高原地区暖昼变冷、暖夜变暖的趋势，高估冷夜在北方地区和华东的变冷趋势；低估暖昼和暖夜在华东地区均增暖的趋势，低估冷昼在西北的变冷趋势。

尽管本文从气候平均、概率分布、年际变率和年际趋势方面评估了CWRF对极端温度指数的模拟能力，但本研究尚未深入分析误差的来源与成因。区域气候模式的误差主要来源于对物理过程和侧边界条件的描述不够准确（刘术艳等,2008），由于极端温度受到气候系统内部与外部强迫过程的复杂影响（黄荣辉,2006），因此模式中多个物理过程参数化方案间复杂的相互作用也十分重要，例如，陆面/海洋—对流—微物理过程、云—气溶胶—辐射过程等，都会从不同程度上影响区域极端温度变化的模拟和预测（王乐,2018）。因此，在本研究的基础上，需要结合精度更高的观测数据，利用CWRF模式较全面的物理过程及方案，进行不同物理过程的敏感性实验，分析关键区域模式模拟的误差来源，并对典型的区域持续性的极端温度事件个例进行物理机制和成因探究，进一步加深对极端温度事件形成机制的理解，改进模式对极端气候事件的模拟和变化的预估。