波流共同作用下潜丁坝受力情况的二维数值研究

罗兰媛 海南省交通规划勘察设计研究院

郭杰 湖北省港路勘测设计咨询有限公司

1.前言

长江南京以下太仓～南通河段一直为长江南京以下著名的卡口航段之一，航道维护水深长期偏低，严重影响长江南京以下深水航道的畅通。对该段进行12.5m深水航道建设，有利于进一步发挥长江口12.5m深水航道治理工程的综合效益。

由于本项目中涉及到的丁坝群除个别丁坝坝根部位在设计低水位期间会露出水面外，其他全部为潜丁坝。丁坝主要受水流以及波浪作用，而现行的《港口工程荷载规范》（JTS144-1-2010）中对于结构物在水下部分所受水流力并没有较为准确的计算方法。

为了能够得到较为准确的混合式潜丁坝结构在波流共同作用下的受力情况，本文建立了二维波流数学模型进行计算，以便对后期将要进行的的结构稳定计算，以及结构内力计算提供一定的借鉴作用。

2.基本资料及数学模型

2.1 基本条件

设计高水位：2.76m（85国家高程系统）

设计低水位：-0.69m

设计高水位对应波高：2.16m；

设计低水位对应波高：1.845m；

波浪周期：T=6s；

流速：3m/s;

结构段顶高程：-1.94m

2.2 设计堤身形式

本工程中通州沙段潜丁坝采用斜坡式与直立式组合的混合式堤身结构，典型结构形式见图1、2。

如图1、2所示，堤身方案一中，采用直径为6m的半圆体下部抛石基床为高4m，底宽约36m，两侧坡比为1:2的混合结构。方案二中将上部结构换为异形沉箱，基床部分与方案一完全相同。

图1 混合式堤身断面（方案一）

2.3 数学模型

本文中数学模型采用标准k-ε方程封闭的N-S方程对流场进行模拟。

图2 混合式堤身断面（方案二）

2.3.1 基本控制方程

连续方程：

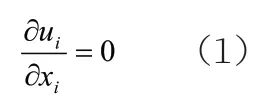
动量方程：

选用标准k-ξ方程用以封闭N-S方程。

紊动动能方程：

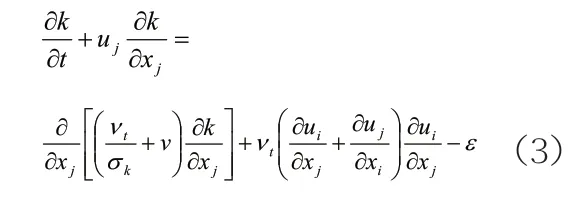
紊动耗散率方程：

以上（1）～（4）各式中，i=1，2，j=1，2，v为流体运动粘滞系数；f1为质量力强度；Cμ为无量纲数；常数σk=1.0，σε=1.3，σε1=1.44，σε2=1.92，均由实验所得；方程经过无量纲化之后ρ=1，v=1/Re。

2.3.2 方程求解

建立的立面二维数学模型在计算波流共同作用时不考虑在水流作用下结构物的变形以及移动，因此为非流固耦合的情况，其中运动方程的离散采用刘清朝等在进行水跃研究时提出的离散方法。

2.3.3 边界条件的处理

（1）固壁边界的处理。计算区域上下边界条件均设定为无滑移边界条件，左右为入流出流边界条件。本文中在其近壁附近采用壁函数技术进行处理。在近壁结点选取时，取近壁处1/2步长为结点。考虑到结构物对于波浪存在的反射作用，为更有效的保证入射波在传递过程中的准确性，将结构物安置位置放置在距造波位置30m处。

（2）自由面的处理。采用VOF法模拟水体自由表面。较为精确的自由面处理技术可以更准确的模拟波浪在传递过程中的变形，最终影响到速度场以及压力场的精确性。能得到较为准确的波压力。

2.3.4 计算结果的处理

由于计算程序并不能计算结构物的受力情况，因此本次计算所采用的结果是将临近结构物表面的水体所受压力等效为结构物所受压力。计算所得到的结果为结构物表面分布的压力情况，在进行结构物稳定计算时，需将其分解为水平方向和竖直方向两部分。

3.数学模型结果验证

为验证计算结果的准确性，采用第一方案结构物在只受波浪作用，不考虑水流力时的结果。从其中选取三个典型位置与《防波堤设计与施工规范》（JTS--2011）中半圆体波浪力计算公式所得结果相比较。

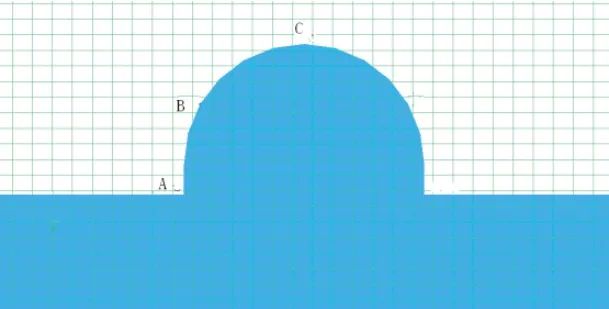
图3 典型位置示意图

表1 方案一设计低水位时计算结果数据对比

图4 方案一设计高水位水压力云图

图5 方案二设计高水位水压力云图

图6 方案一设计低水位水压力云图

图7 方案二设计低水位水压力云图

图8 位置A所受波压力随时间变化图

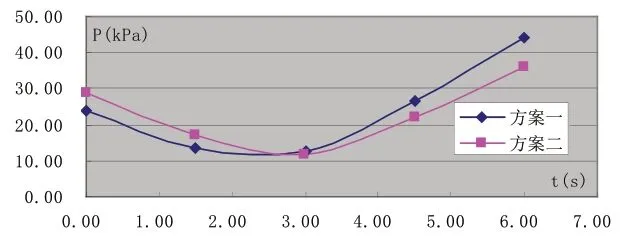
图9 位置B所受波压力随时间变化图

图10 位置C所受波压力随时间变化图

图11 位置A所受波压力随时间变化图

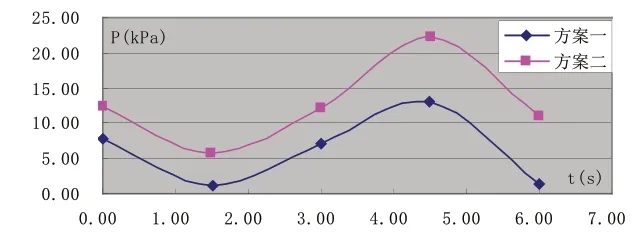
图12 位置B所受波压力随时间变化图

如图3所示，A、B、C三点分别位于半圆体距下部抛石基床顶面0.00m、2.76m、5.00m的位置。

数值计算所得到的结果为结构体外表面所受的压力。为便于后文的对比分析，将结构体一侧所受的水平方向的压力与沿中轴线对称的一侧所受的压力相减，从而得到结构体在各个高度所受到的合力。各位置水平方向的合力与公式计算结果比较见表1。由表1可知，模型与公式计算结果十分接近。

4.水流波浪共同作用的受力分析

在原数学模型中增加3m/s的流速，对两种结构分别在设计高水位，设计低水位两种条件下进行计算。所得计算结果见图4～图7。

为对比两种结构在设计高水位及设计低水位时所受水压力随周期的变化情况，分别取图3中A、B、C处的三个点在一个波周期内所受水压力的数值进行分析。

设计低水位时，图8～图10所描述的为一个完整波浪周期内，其中横轴为一个波周期内不同的时刻（s），与之相对应的波浪相位从第0s到第6s分别为平衡位置、波峰、平衡位置、波谷、平衡位置；纵轴为该点由于波流共同作用所产生的压强（kPa）。两种方案的断面在三种不同位置所受的波浪与水流的压力变化情况。可以看出，在水流及波浪共同作用下，方案二的结构物所受的压力要稍大于方案一。

图11～图13所描述的为设计高水位时，两种方案的断面上三个不同位置所受的波浪与水流的压力变化情况，其中横轴为一个波周期内不同的时刻（s），与之相对应的波浪相位从第0s到第6s分别为平衡位置、波峰、平衡位置、波谷、平衡位置；纵轴为该点由于波流共同作用所产生的压强（kPa）。可以看出，在水流及波浪共同作用下，方案二的结构物所受的压力要稍大于方案一。

图13 位置C所受波压力随时间变化图

最后，通过表4-1～4-6所述内容可以看出，结构方案一优于方案二。

5.成果应用

结构物在波流共同作用下受力成果可用于结构物稳定计算和内力计算，从而达到合理确定结构物断面的目的。

6.结论

本次计算通过二维数学模型以模拟在波流共同作用下两种方案结构物所受波浪及水流作用力，可以得出以下结论：

所用计算程序基本上能够满足对于结构物所受波流共同作用下的受力情况进行计算。

本次计算为后期进行的结构物稳定计算以及内力计算提供了一定的借鉴。