基于MPC-SSA的动态无人机航路规划

仇钧正，宁芊

（四川大学电子信息学院，成都610065）

0 引言

现代战争中无人机发挥着越来越大的作用，无人机的军用甚至可以追溯到一战时期。自20世纪70年代以来，军用无人机广泛出现在局部战争中，无人机的发展也被越来越多的国家置于重要地位[1]，军用无人机有望重塑21世纪的作战模式。无人机可以在战场或者敌后执行各种任务，如侦察、监视、电子干扰、攻击拦截等。那么如何让无人机可以在复杂的地理环境和雷达、武器等威胁环境下可以仍可以顺利执行任务，就至关重要了。近十几年来人工智能的兴起引发了大量的算法相关研究，在航路规划问题上学者们提出了众多算法以应对各类复杂环境。

启发式算法（Heuristic Algorithm）是一种基于直观或经验构造的算法，在可以接受的花费（计算时间、计算空间）下给出待解决优化问题的一个可行解，该可行解与最优解的偏离程度一般无法预计。而元启发式算法（Meta-Heuristic Algorithm）是启发式算法的改进，一般结合了随机算法和局部搜索算法。因为元启发式算法可以快速找到相对最优解，所以适合解决动态航路规划这种复杂条件下的寻优问题。文献[2]使用改进的粒子群算法对编队无人机航路进行寻优，文献[3]使用灰狼算法进行三维空间的无人机航路规划，文献[4]针对动态航路规划问题提出了一种结合粒子群算法和遗传算法的路径规划算法，文献[5-6]综合了遗传算法和蚁群算法进行军用无人机在复杂环境下的航路规划，这些文献使用不同的元启发式算法针对具体环境下的无人机航路规划。本文采用一种具有优秀寻优性能的新式元启发式算法社会蜘蛛算法（SSA），结合模型预测控制技术（MPC）进行战场环境下的航路规划。航路规划过程中通过马尔科夫生存状态模型来对无人机的生存状态概率进行实时评估，直观观察航路规划全过程中无人机的生存状态变化和生存概率。

1 无人机航路规划问题建模

1.1 威胁模型

战场下无人机的威胁主要来自于以下几个方面：山地、丘陵、盆地等复杂地形；敌方侦察雷达以及敌方地面火力。

地形威胁的场景主要包括高低差较大的山地和盆地，本文研究的场景建模中采用三维空间建模，模拟真实的高山和盆地地势，并在无人机生存代价评估时考虑飞行高度代价。

雷达威胁区域可以简化为顶面为球面的圆锥体区域[7]，其垂直投影为扇形，水平投影为圆形，如图1所示。最大探测范围为R即雷达探测半径，Pos为无人机当前所在位置，无人机与雷达中心的距离为r。

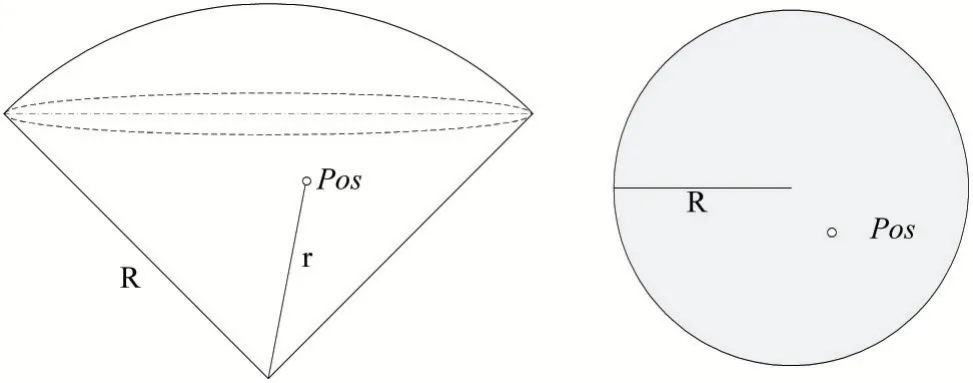
图1

无人机距离雷达中心越近，被侦察到的概率就越大。无人机被雷达侦察到的概率计算如公式（1）所示。在1.2小节中会介绍将雷达威胁模型与马尔科夫生存状态模型相结合进行无人机生存状态评估。

本文中地方火力模型设置为火力覆盖网，与雷达威胁模型类似，敌方火力覆盖区域也简化为顶面为球面的圆锥区域。相比于雷达威胁区域，敌方地面火力具有更大的威胁，无人机如果在多个雷达重叠区域或者雷达与敌火力重叠区域飞行将会受到叠加的威胁，1.2小节中将着重讨论这一问题。

1.2 马尔科夫生存状态模型

本文利用时间连续状态的离散马尔科夫链建立无人机生存状态模型，模型中包含五种生存状态[8]，分别是未被探测、被侦测、被追踪、被攻击和被击落，简记为U、D、T、E、H。通过计算并记录无人机飞行过程中的状态转移情况。

1.2.1 状态转移强度

无人机飞行过程中，其状态会在上述五种生存状态之间转移，根据马尔可夫性质，状态转移只会发生在相邻的状态之间。例如无人机可能从未被侦测状态转移到被侦测状态，但是不会从未被侦测状态直接转移到被攻击状态。在该马尔可夫链中，被击落（H）状态为吸收态即不存在从被击落（H）状态转移到被攻击（E）状态的可能性。相邻状态之间的转移概率计算方式如下：

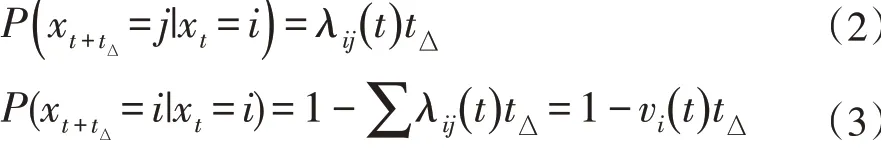
式中i、j分别表示生存模型中的某两个相邻且不同的生存状态，tΔ表示无限小的时间，λij()t表示当前时刻由i状态转移到j状态的转移强度，P描述了状态之间的转移概率，v i()t为转移到其他状态的转移强度和。观察上述两式可知，当前时刻下无人机处于i状态的条件下，在tΔ后转换为j状态的概率只依赖于当前时刻和tΔ。

转移强度描述了无人机从一种状态转移到另一种状态的变化可能性，转移强度的确定涉及到两个因素：无人机与雷达区域、火力区域之间的相对位置和转移前后的无人机状态。

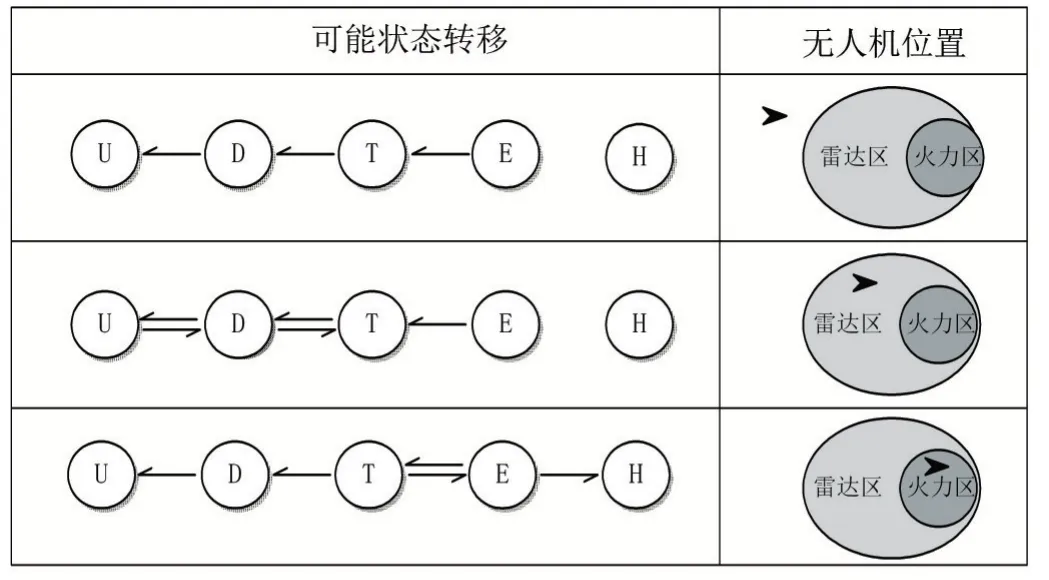
图2

图2 展示了不同的相对位置条件下无人机可能出现的状态转移情况，例如无人机既不在雷达探测范围也不在火力覆盖范围，那么无人机不会出现被雷达探测到这一状况，也就是无人机不会从未被侦测状态转移到被侦测状态，所以此时状态U到状态D的转移强度应设置为零。如果无人机此前处于被攻击、被追踪、被侦测状态，那么离开威胁区域后，无人机有机会回到更安全的状态，所以均应设为大于零。图示三种情况从上到下依次为：无人机既不在雷达区域内也不在火力区域内；无人机在雷达区域内，但不在火力区域内；无人机在雷达与火力重叠区域。转移强度的最大值参考文献[9]，转移强度随无人机距离威胁区域中心的距离变化，计算如（4）所示：

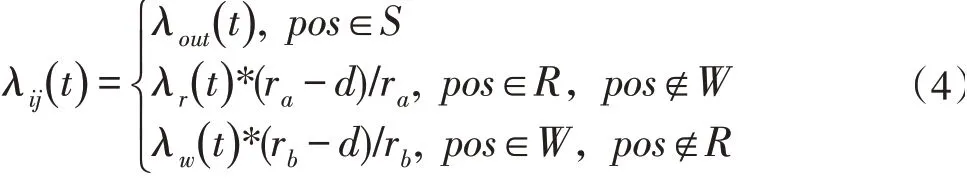
式中d表示无人机距离雷达区或火力区中心的欧氏距离，r a、r b分别表示雷达区域和火力区域的覆盖半径，S、R、W分别表示安全区域、雷达区域和火力区域。为无人机在威胁区域外的最大转移强度，分别表示无人机在雷达区域内和火力区域内的最大转移强度。如果无人机位于火力区和雷达区的重叠部分，将会面对更严重的威胁，此时需要使用如下公式计算转移强度：

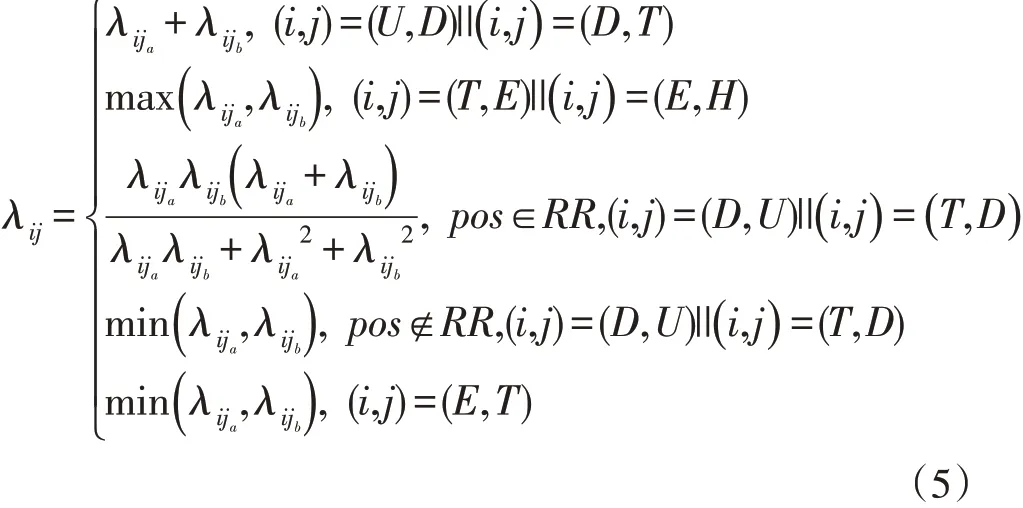
λija表示第一威胁区域的转移强度，λija表示第二威胁区域的转移强度，重叠的两个威胁区域可以是雷达区域或者火力区域，RR表示重叠的两区域都是雷达区域。由上式可知，两个重叠雷达区域对无人机恢复安全状态的影响要小于存在火力区的重叠区域[10]，同时无人机一旦进入被攻击（E）状态，相对不容易再回到前一个状态（T）。

1.2.2 状态概率和生存代价

通过上面讨论的状态转移强度可以计算无人机飞行过程中的状态概率，本文给与每种状态一个状态代价来计算无人机飞行过程中的生存代价。b i表示无人机飞行过程中处于i状态单位时间的代价，C d为无人机从被攻击（E）转移到被击落（H）的击落代价。通过评估一条步长为n的飞行过程中的累计生存代价，来判断这条路径的优劣。P i(n)为第n步长时无人机处于i状态的状态概率，ξ(n)为经过n步长后这一段路径的累计生存代价，并假设两步长间的执行时间为Δt，则动态路径的生存概率和生存代价如下公式进行计算：

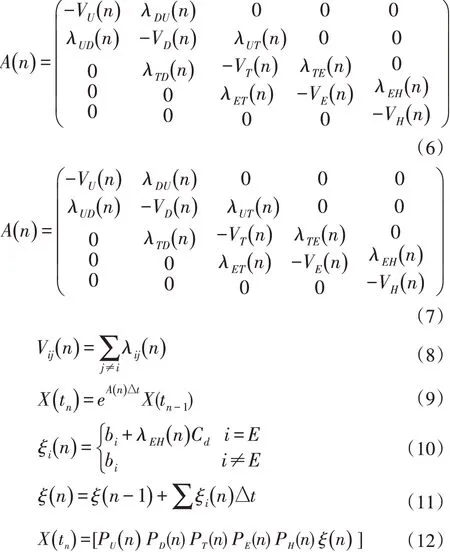
式中A(n)为转移强度矩阵，X(t n)记录路径经过n步长后的状态概率和累计生存代价。

2 MPC-SSA航路规划算法

2.1 社会蜘蛛算法

社会蜘蛛算法（Social Spider Algorithm）是一种模仿蜘蛛种群行为的元启发式算法，蜘蛛在自然界常被认为是独居动物，但是也存在有具有一定社会行为的蜘蛛种群，蜘蛛利用织网震动来进行信息交换，完成交配或捕猎。求解空间可以看作蜘蛛网，求解空间中的随机样本点看作在网上的蜘蛛。在文献[11]中模拟了蜘蛛种群的交配过程，通过繁衍适应度值更高的后代来筛选最优样本点，该方法具有蚁群算法和遗传算法两者的思想。Yu J J Q等人[12]模拟了蜘蛛种群的集体捕猎行为，提出了另一种社会蜘蛛算法，相比于文献[11]中的社会蜘蛛算法，该算法的收敛性更快。本文在该算法基础上，将其运用到无人机路径规划的寻优过程，添加了MPC方法提高路径的总体质量。

社会蜘蛛算法中将解空间的样本点看作没有质量和大小的蜘蛛，在算法开始时，会在网（解空间）初始化多个蜘蛛。每只蜘蛛根据自己的位置计算适应度值，并向其他蜘蛛发送震动，同时每只蜘蛛都会接收来自其他蜘蛛的震动，根据震动强度和自己的历史移动记录进行移动。每一个蜘蛛s需要保存下列参数信息：

●s在网上的位置

●s位于当前位置时的适应度函数值fi t

●在前次迭代中s的目标蜘蛛s tar

●s距离上次目标蜘蛛的更换经过的迭代次数iter

●s在前次迭代中的移动m

●前次迭代中指导s进行移动的维度码

前两个参数描述了蜘蛛当前的信息，其他参数决定蜘蛛本次迭代中的爬行过程。社会蜘蛛算法的关键参数是震动强度，每个蜘蛛都会接收到种群所有其他蜘蛛的震动，震动强度由两蜘蛛间的距离和蜘蛛的适应度值决定。记蜘蛛a在t时刻所在位置为P a，用V(Pa,P b,t)表示t时刻蜘蛛b受到蜘蛛a的震动强度，V(Pa,P a,t)表示蜘蛛a产生的震动强度，将蜘蛛a的适应度值记为f(P a)，那么震动强度可以表示为：

C是一个自定义的参数，比所有可能的适应度值都小。蜘蛛b受到蜘蛛a的震动强度表示为：

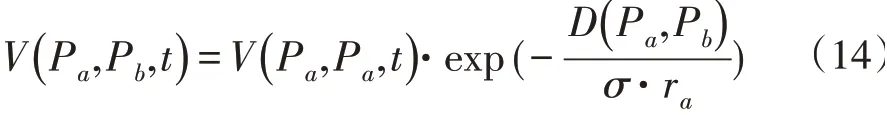
D(P a,P b)表示两蜘蛛间的欧氏距离，r a为人为控制参数，该参数越大，距离对震动强度的影响就越小。

搜索过程主要分为两个阶段：

（1）初始化阶段：在固定的解空间里随机分散生成若干个样本点即蜘蛛，计算这些点的适应度值和震动强度，将它们的目标蜘蛛s tar设为自己。

（2）迭代阶段：每次迭代都会改变处于网上的蜘蛛的位置，迭代阶段流程如图3所示。

以蜘蛛a为例，在计算了全部蜘蛛的适应度值和震动强度后，选择收到震动中最大的一个蜘蛛，将其与前一次的目标蜘蛛的当前震动强度进行对比，用震动较大者更新为新目标蜘蛛s tar。

之后蜘蛛a会向s tar方向进行随机游走，蜘蛛保存信息中的维度码将指导其运动，维度码m是取值为0或1的长度为D的矩阵，D是解空间维度。在每次迭代中，蜘蛛a的维度码分别有1-p iter c的概率变化P c为人为规定概率，小于1。iter为蜘蛛a存储的信息中距离上次目标蜘蛛的更换经过的迭代次数，如果蜘蛛a多次迭代过程中都没有改变目标蜘蛛，那么它本次迭代中随机游走的概率就会变大，该性质保证了算法不易陷入局部最优。蜘蛛随机游走后的目标位置按照如下公式计算为：

式中ma,i为维度码随机变化后蜘蛛a在第i个维度上的维度码。r标示种群中的随机蜘蛛，蜘蛛a随机游走时部分维度向目标蜘蛛移动，部分维度向随机蜘蛛移动，以此来避免陷入局部最优。蜘蛛a确定目标位置后按公式（16）进行移动。

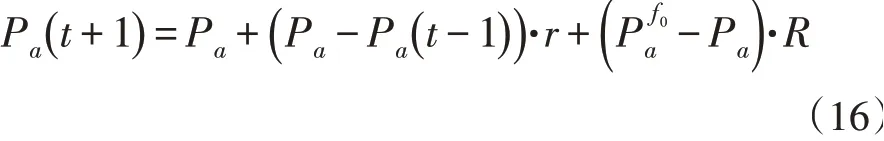
蜘蛛a更新后的位置为其当前位置与惯性位置和目标位置的加和。R为0-1间的随机数。如果蜘蛛在随机移动中超出了解空间，本文的解决方法是边界法，即限制维度的最值，超过则按最值进行计算。

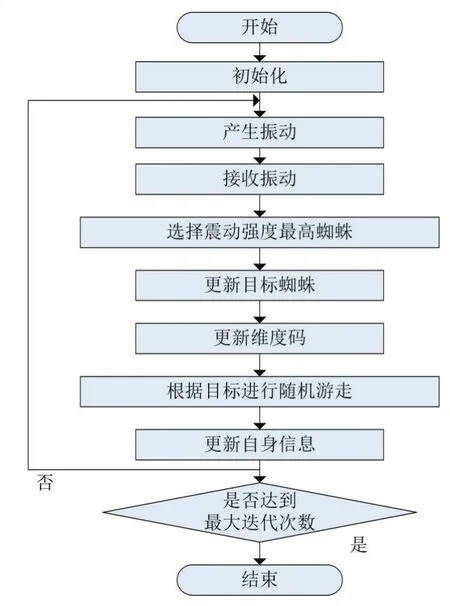
图3

2.2 适应度函数计算

在算法执行过程中，适应度函数作为判断航路优劣的依据，也指导蜘蛛在网上的移动。本文综合无人机航行中多种代价的加权和作为适应度函数。

（1）生存代价：在1.2小节中讨论了基于马尔科夫链的五状态生存模型，通过式（7）-（12）可以计算无人机在第n次搜索后的生存代价C s(n)

（2）任务代价：经过任务点并完成任务是无人机的重要目标，任务完成代价可如下式计算：

P tar为下一个要去的任务点，p n为无人机当前位置。

（3）参考路径代价：无人机飞行过程中，需要尽快飞向任务点，引入参考路径代价即无人机，当前位置与起点到任务点连线的垂直距离：

其中L为参考路径，即起点到任务点的连线。

（4）油耗代价：

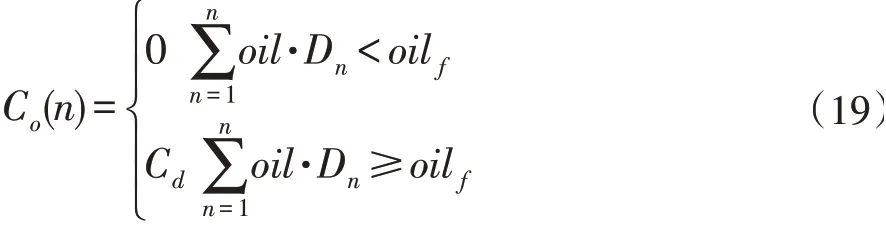
oil表示单位距离耗油量，oil f表示无人机总油量，当航路油耗大于总油量时，该航路需要承担C d的代价

（5）高度代价：本文限制了无人机可以飞行的最高高度Hmax和最低高度Hmin与油耗代价类似，如果航路中无人机高度超出范围，该航路需要承担C d的代价。

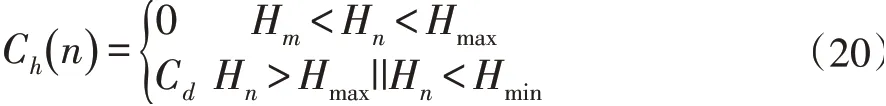
对上述5种代价分别设置权重为：W s,W q,W r,W o,W h，则适应度函数由式（21）表示：

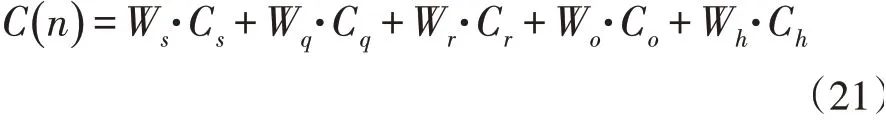
2.3 模型预测控制

本文模拟的是实时战场环境下无人机在敌侦察雷达区域和火力区域执行任务，由于环境威胁较多，无人机飞行过程中执行悬停转向会让其处于危险之中，因此本文对无人机飞行过程中的转向角进行了限制，即当前目标点会影响后续目标点的选区。无人机在飞行过程中，如果只针对当前点寻找下一个目标点，无人机会出现顾此失彼的情况，例如：低威胁区域有两个较优点A和B，通过算法选择A点，但是选择A点势必会让无人机接下来飞入高威胁区域，此时B点应该是更好的选择，为了避免出现顾此失彼的情况，引入模型预测控制。

模型控制预测[13-14]MPC作用机理描述为：在每一个采样时刻，根据获得的当前测量信息，在线求解一个有限时间开环优化问题，并将得到的控制序列的第一个元素作用于被控对象。MPC可以分为三步：

（1）预测未来动态：本文使用MPC-SSA算法在航路规划过程中单单只寻找下一个目标点，而是寻找步长为N的航迹。

（2）求解开环优化问题：通过1.1小节和1.2小节中介绍的威胁模型及马尔科夫生存状态模型计算步长N的航迹的总体适应度值，选取最优航迹作为解。

（3）将优化解的第一部分作用于系统：在获取步长为N的最优航迹后，只选取其前E个步长让无人机执行。

循环上述三步操作，算法每次执行会让无人机飞行E步，直到无人机达到目标点。社会蜘蛛算法部分可以看作MPC控制器，步长为N的航迹作为预测范围，预测范围约束包括：最大最小水平转向角αhmax,αhmin，最大最小竖直转向角αvmax,αvmin，最大最小速度vmax，vmin。在3.2小节的结果分析中会比较使用模型控制预测的MPC-SSA算法和不使用模型控制预测的SSA的结果。

3 仿真与分析

3.1 参数设置

本文仿真实验环境为：Intel Core i5-7300，8G内存硬件环境，MATLAB 2016b版软件环境。仿真设置参数如表1-表5。

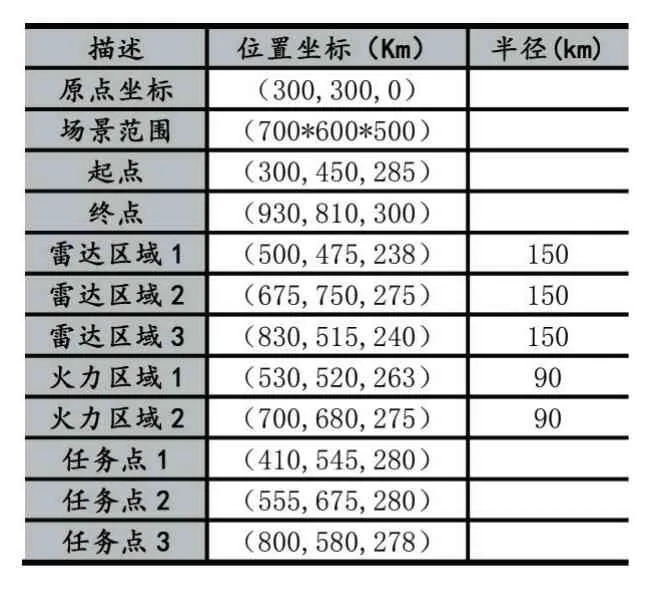
表1 场景参数

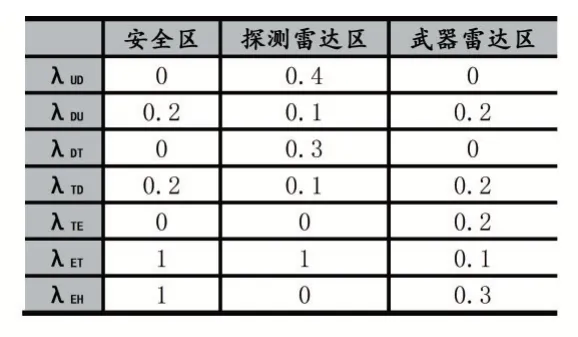
表2 转移强度参数

表3 状态代价参数

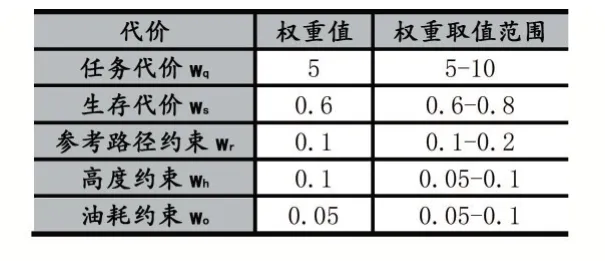
表4 权重值设置

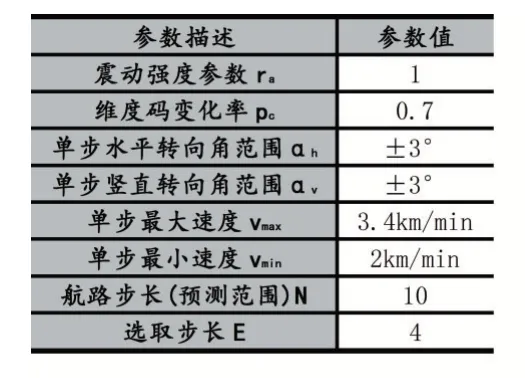
表5 其他参数设置

3.2 结果分析

3.2.1 MPC-SSA与PSO对比

通过MPC-SSA算法和传统PSO算法进行路径规划结果分别如图3.1（a）和图3.1（b）所示。

本实验为了对比SSA与PSO算法，在PSO算法的基础上也添加了相同的模型控制预测

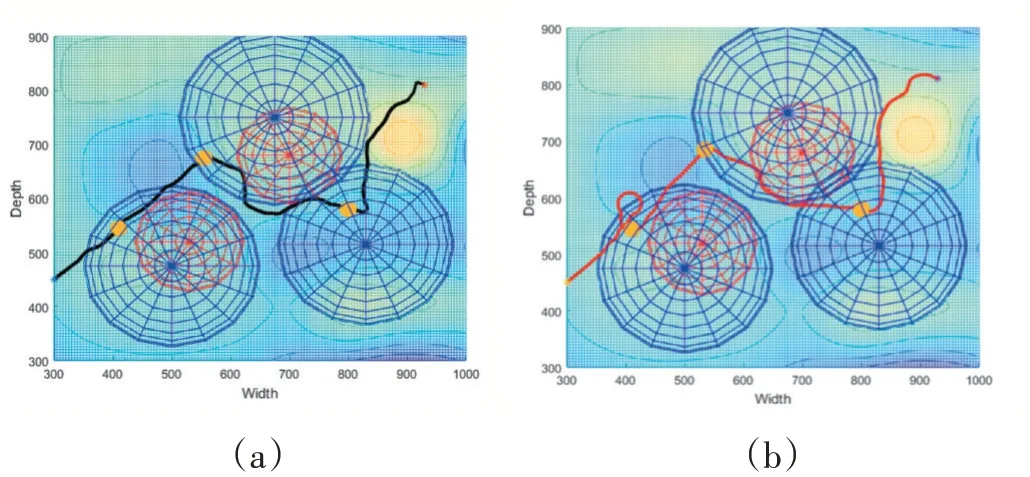
图4

图4 中黑色曲线即为无人机飞行路线，蓝色区域为地方雷达区域，红色区域为地方火力区域，黄色点为任务点。结果图为俯视图，明亮黄色区域为高海拔地形，暗淡蓝色区域为低海拔盆地。观察图4（a）可以发现，使用MPC-SSA算法进行路径规划，无人机在完成任务后可以迅速脱离火力区域，并选择合适路径前往下一个任务点。对比图4（b），使用传统PSO算法进行路径规划的无人机完成任务后会进入火力区域，且在第一个任务点附近出现了不必要的盘旋状态。通过观察分析可以初步判定MPC-SSA算法相比PSO具有更好的寻优性能。

本文在仿真过程中统计了无人机飞行过程中处于各个状态的状态概率，图5（a）为图4（a）路径对应的航路生存状态概率，图5（b）为图4（b）对应航路的生存状态概率。图中横坐标为无人机飞行的步数，纵坐标表示无人机处于该步时生存状态的概率。对比两图可以直观地看出MPC-SSA在性能上更加优秀，无人机处于威胁状态的时间更短，被击落的概率为零，而观察图5（b）可以看到，基于PSO算法规划的航路有相对较高的概率被击落。

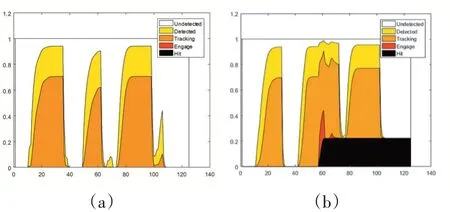
图5

3.2.2 MPC-SSA与SSA对比

本文通过MPC-SSA与SSA在相同环境和参数下进行结果对比来显示MPC在路径规划中的重要性。观察图6（b）和图7（b）可以看出，在不使用模型预测控制的方案下，无人机无法避开火力威胁区域，具有很大的被击落概率。同时无人机在飞向目标点的途中也可能出现盘旋等肉眼可见的失误。这是由于无人机飞行中受到转向角速度等因素限制，先确定的航路点会影响后续航路的规划，出现顾此失彼的情况。

此外本文统计了几种算法在相同环境下的航路长度、飞行时间等参数进行直观的数据比对。在战场环境下，不影响任务执行和完成的条件下，航路长度、飞行时间都是越短越好。适应度值为每次路径规划后航路的平均适应度值，在本实验环境下，航路平均适应度值越小证明航路的性能越好。

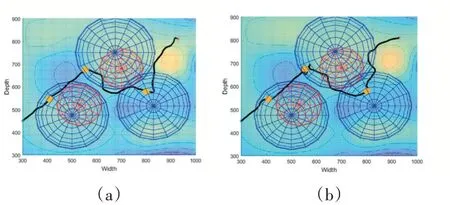
图6

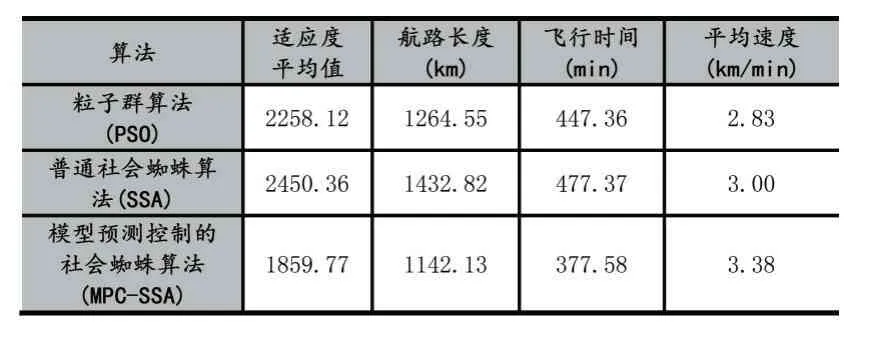
表6 算法性能对比

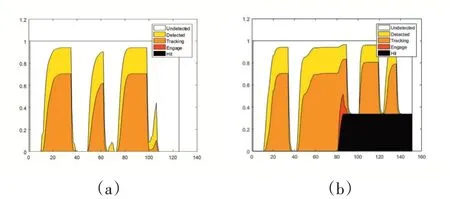
图7

4 结语

本文提出了一种基于社会蜘蛛算法并结合模型预测控制的一种动态航路规划算法。通过理论论述和仿真实验对比了该算法与传统粒子群算法和无模型控制下社会蜘蛛算法的性能，证明了该算法具有较强的寻优性能和跳出局部最优能力，是复杂战场环境下无人机动态航路规划算法的较优选择。