分数阶预估-校正方法在求解二维多项时间分数阶方程中的应用
赵豪杰,张秀英
(郑州铁路职业技术学院,河南 郑州 451460)
近年来,由于在描述具有记忆特性的物理现象和过程中的优势,分数阶偏微分方程作为有效的建模方法而引起了人们的极大关注.分数阶微积分已广泛应用于物理学、生物学、黏弹性流体和控制理论等领域[1-2].通过使用分数阶偏微分方程来描述实际问题中复杂的物理过程,如在非牛顿流体流动问题中,许多学者分析和研究了分数阶Maxwell黏弹性流体[3]、分数阶Oldroyd-B流体[4]、分数阶Burgers流体[5]等流动问题,多项时间或时空分数阶偏微分方程在研究中起着重要的作用.随着分数阶方程的广泛应用,众多学者开始对快速有效的方法求解不同类型的多项时间或时空分数阶偏微分方程的问题进行研究.文章研究了二维多项时间分数阶方程的求解问题,多项时间分数阶导数为Caputo类型,其阶数随机属于区间(0, 2).提出了分数阶预估-校正方法来计算多项时间分数阶方程,数值结果证明了理论分析的有效性.这些计算方法和理论分析也可以推广到求解其它实际问题中的多项时空分数阶模型.
1 分数阶预估-校正方法的建立
分析下列二维多项时间分数阶方程的求解问题[3]:

(1)

(2)
边界条件为:u(0,y,t)=u(L1,y,t)=0,u(x,0,t)=u(x,L2,t)=0,0 (3) 把方程(1)改写为分数阶偏微分方程组: (4) 由方程(1)的初始条件(2),得方程组(4)相应的初始条件为: (5) 定理1多项时间分数阶方程(1)及其初始条件(2)等价于分数阶偏微分方程组(4)及相应的初始条件(5). 证明参考文献[6]的证明方法,即得结果,过程从略. 对于一般的分数阶微分方程组: (6) 及其初值问题,使用分数阶预估-校正方法进行求解,过程如下: 对于如下方程 其中,0<γl<1,上述初值问题与下列Volterra积分方程是等价的,即 (7) 把方程的时间和空间区域分别划分网格,即:tk=kτ,k=0,1,…,N,τ=T/N;xi=ih1,i=0,1,…,M1,h1=L1/M1;yj=jh2,j=0,1,…,M2,h2=L2/M2(N,M1,M2为正整数).分别使用分数阶Adams-Bashford公式和分数阶Adams-Moulton公式[7]作为预测值和校正值进行计算. (8) (9) 用上述数值方法求解方程组(4),由分数阶Adams-Bashforth公式确定预估值为(l=1,2): (10) (11) 由分数阶Adams-Moulton公式确定校正值为(l=1,2): (12) (13) 关于分数阶预估-校正方法的误差估计,给出下面定理: 定理2使用上述式(10)-式(13)分数阶预估-校正方法求解方程组(4),计算结果误差为: 证明参考文献[8]的证明方法,即得结论,过程从略. 为了证明式(10)-式(13)分数阶预估-校正方法的实际计算效果,构造下列有解析解的分数阶方程分别进行计算: u(0,y,t)=u(2,y,t)=0,u(x,0,t)=u(x,1,t)=0,t>0 分析得到该算例的解析解为u(x,y,t)=t3xy(2-x)(1-y).使用分数阶预估-校正方法求解算例,得到数值解与解析解之间的误差,如表1所示. 表1 分数阶预估-校正方法与解析解之间的误差(T=1.0) 从表1的计算结果可以得到,随着空间和时间划分步长的减小,误差满足分析的理论误差.使用该方法计算时,计算速度较快并且数据存储空间要求较小. 文章提出了有效的计算二维多项时间分数阶方程的分数阶预估-校正方法,并对数值方法进行了相关理论分析,数值计算结果验证了理论分析的有效性.使用分数阶预估-校正方法计算时速度较快,并且不需要对大量数据进行存储,需要注意的是该方法是条件稳定的,在计算时要保证所给的时间步长足够小.








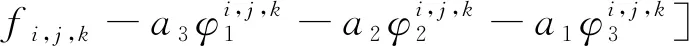



2 算法实例验证分析



3 结论

