考虑环境温度和连续射弹量的某机枪抽壳故障仿真预测

冯文浩，方 峻

(南京理工大学， 南京 210094)

速射武器抽壳过程在高温、高压、高速的过程中进行，会面临卡壳以及弹壳断裂的问题，这些问题主要是由枪械的抽壳机构工作失效引起的。因此研究在不同环境温度和射弹量条件下抽壳机构的故障率对武器在工作状态下减小故障率有重要作用。

有不少学者对武器抽壳过程中的一些影响因素进行过研究。在理论研究上，吴志林等[1]建立了高压抽壳理论，宋广惠等[2]建立了壳机力和抽壳力的数学模型。针对抽壳机构的结构研究，卫丰等[3]讨论了初始间隙等因素对发射应力和抽壳力的影响。康艳祥等[4]分析了初始间隙、弹膛壁厚、摩擦因数与抽壳力之间的关系。谭波等[5]分析了抽筒模板下移和抽筒左右位置变化对抽壳的影响。在环境因素方面，杨吉王明广等[6]分析了温度对抽壳的影响。此外，林等[7]对抽壳时药筒的应力变化进行了仿真分析。但是国内对枪械的抽壳故障率研究几乎空白。

本文运用有限元软件ANSYS模拟某型机枪在不同环境温度和射弹量条件下的抽壳过程，把环境温度分为3种，分别是高温、常温和低温条件，选环境温度、射弹量、摩擦因数3个影响因素进行分析。针对该机枪抽壳失效时弹壳断裂情况进行分析，采用材料力学中的第一强度理论，通过蒙特卡洛法来计算不同环境温度和射弹量条件下抽壳的故障率。

1 基本理论分析

1.1 总体方法及流程

本文针对某型机枪在不同环境温度和射弹量条件下抽壳故障率进行计算，通过有限元计算出某型机枪在不同环境温度、射弹量和摩擦因数下抽壳过程中的最大抽壳阻力和弹壳最大主应力，并通过响应面分析得出弹壳最大主应力的拟合公式，再根据拟合公式求解出不同环境温度以及射弹量条件下弹壳的最大主应力的均值和标准差，通过蒙特卡洛法进行故障率仿真，得出抽壳故障率。总体流程如图1所示。

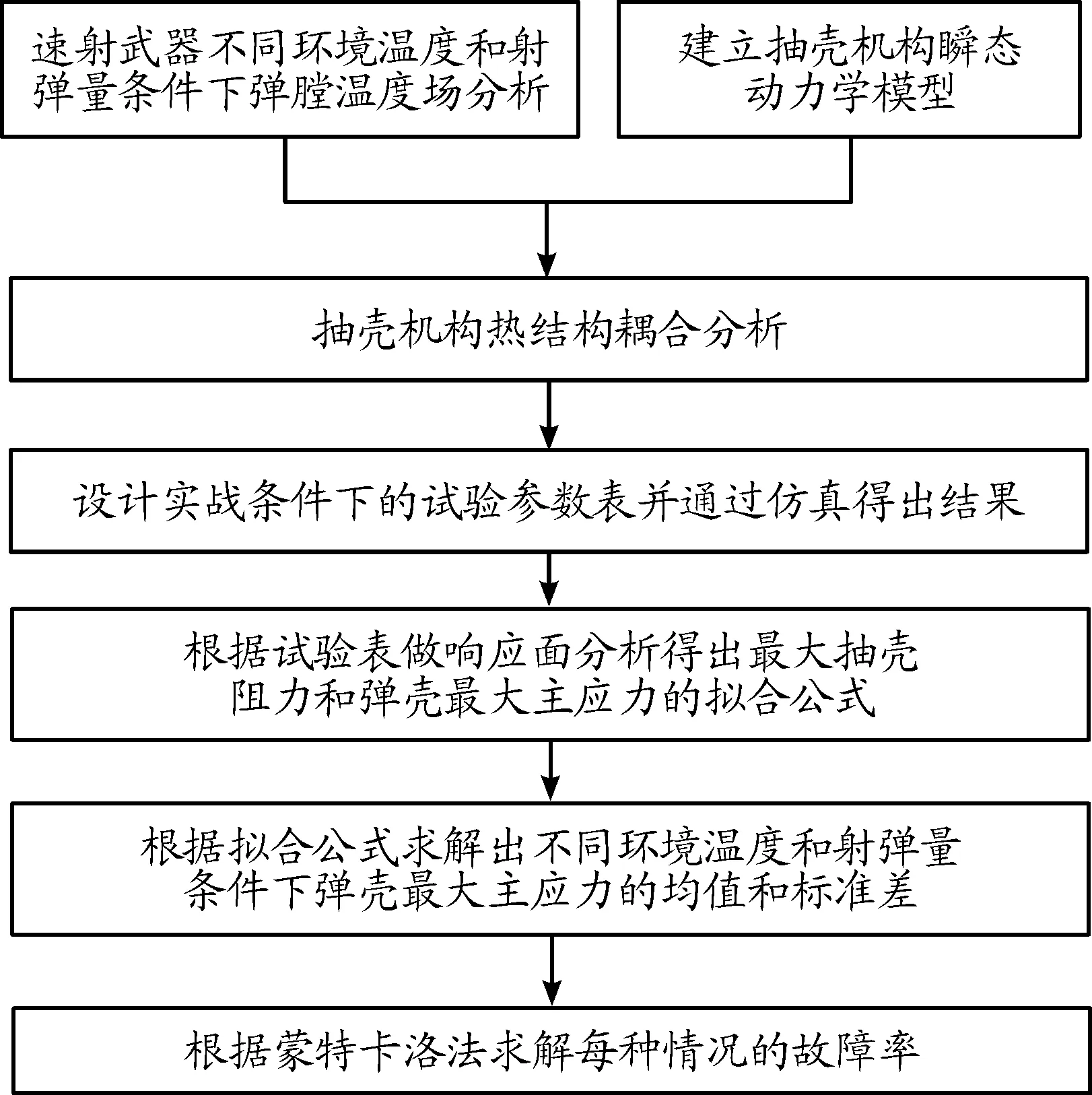
图1 抽壳故障率求解总体流程框图

1.2 故障原因分析

在不同的环境中，枪械面临不同的环境因素，导致抽壳故障的原因也不同。在热带沙漠地区，影响抽壳故障主要是温度和沙尘，热带沙漠地区装药温度较高因此膛压相对较高，同时高温使得润滑油蒸发较快以及沙漠地区的沙尘影响使得摩擦因数增大，引发抽壳故障。在常温沙尘地区，抽壳故障主要是由沙尘进入枪膛引起的摩擦因数变大。在高原或冰原寒区，装药温度低，枪械的膛压较低，且温度过低引起润滑油凝固使得摩擦因数增大，产生抽壳故障。

1.3 抽壳阻力力学分析

抽壳时膛内残余一定的压强，不同装药温度下的压强也不同，温度修正系数可以通过压力的全冲量来体现。

(1)

因此高温或低温下，压力的全冲量为：

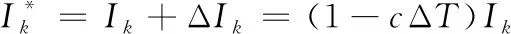
(2)

在刚性闭锁的情况下，抽壳一般在膛压下降到某一值时开始。抽壳阻力不仅与膛压、弹壳与弹膛的材料及尺寸有关，还与弹壳在弹膛内的长度有关，随着抽出的长度增加，抽壳阻力逐渐减小。若将弹壳等效视为n个圆筒，抽壳阻力一般可用于下式描述：

(3)

式中，n为切取轴向长ΔLi的弹壳环数量；f为弹壳弹膛之间的摩擦因数；pi为第i个环与弹膛的挤压力；p为抽壳时的剩余膛压；d为武器口径[8]。

1.4 故障率分析

针对抽壳时弹壳断裂的情况，根据材料力学第一强度理论或者第二强度理论[9]判定断裂失效形式。第一强度理论认为：当最大拉应力达到某一极值，材料断裂。当弹壳最大主应力超过最大许用拉应力时，材料发生损坏，没有超过最大许用拉应力则认为满足强度设计要求。

故障率采用蒙特卡洛法进行分析，该方法是通过随机模拟和统计试验来求解结构可靠性的近似数值方法。当用蒙特卡洛方法求解某一事件的概率时，可以通过抽样试验的方法，得到该事件出现的频率，将其作为问题的解[10]。

2 有限元模型

2.1 基本假设

弹壳在工作过程中的受载变形过程是非常复杂的，高温高压，时间极短，还涉及到弹壳弹膛材料的弹塑性变形，材料间的接触摩擦等，要求出完整的理论解非常困难。在此对模型作如下假设：

1) 塑性材料变形规律符合双折线形[11]。

2) 热应力分析过程中进行如下假设：忽略弹膛外壁向空气的导热；不考虑摩擦生热；忽略辐射放热；假设热对流是稳定的[12]。

3) 由于抽壳过程与枪机形状无关，将枪机简化成一个简单的圆柱，有限元模型如图2所示，共划分网格单元 13 749个，网格节点64 479个。弹壳尾部采用四面体网格，其余部分采用六面体网格。

2.2 材料参数

弹壳材料采用20号钢，由于在抽壳过程中弹壳不仅存在弹性变形而且也存在塑性变形，因此在仿真过程中采用双线性弹塑性模型。弹膛材料以及闭锁机构采用身管钢，在抽壳过程中只有弹性变形因此采用弹性模型。弹膛表面有一层均匀的镀鉻层，镀鉻层采用弹性模型。材料的力学性能参数如表1[13]和表2[14]所示。

图2 抽壳机构有限元模型示意图

表1 身管和镀鉻层的力学性能参数

表2 弹壳的力学性能参数

2.3 载荷条件

根据内弹道方程计算出弹壳爆炸过程中产生的压强和温度，对弹壳内表面施加均匀的随时间变化的压强。压强随时间变化如图3所示。

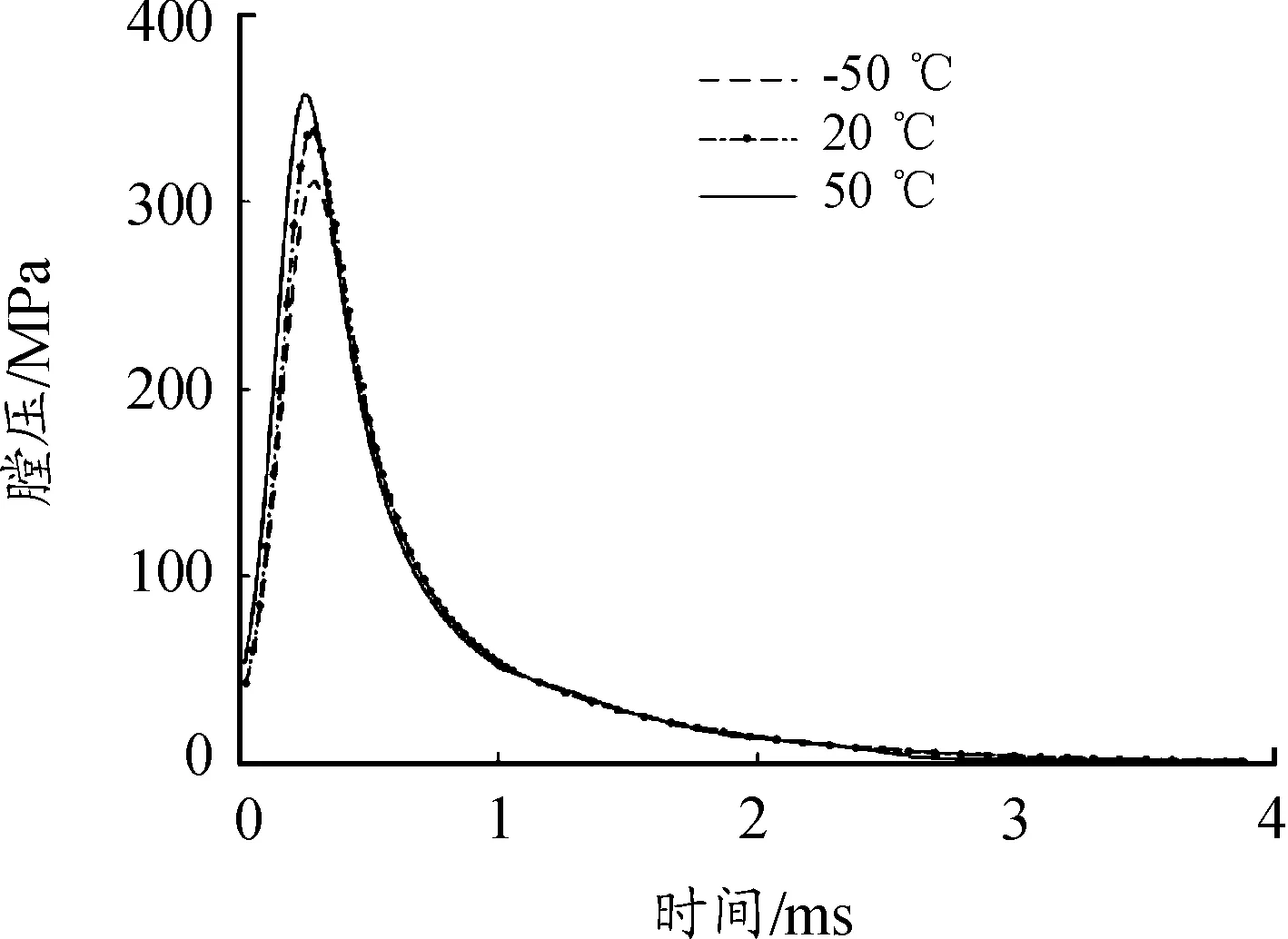
图3 不同温度下的平均膛压-时间曲线

内弹道时期火药燃气温度是时间或弹丸位置的函数，在求解内弹道参数时，通过下面的公式算出：

Tg(t)=[1-(k-1)φqv2(t)/(2gfwψ)]T1

(4)

式中:v(t)为火药弹丸运动速度；k为绝热指数；w为装药量；f为火药力；φ为虚拟系数；q为弹丸质量；ψ为火药燃去部分百分比；T1为火药爆炸温度。

后效期火药燃气温度变化规律为：

(5)

式中：Tk为内弹道结束时膛内火药燃气平均温度；Tbw为火药爆炸温度；Ta为后效期结束时刻膛内火药气体平均温度；tndd为内弹道持续时间；thxq为后效期持续时间。

火药气体温度随时间变化如图4所示。

内弹道时期和后效期的火药燃气放热系数为：

(6)

式中：tp为弹丸在膛内的运动时间。

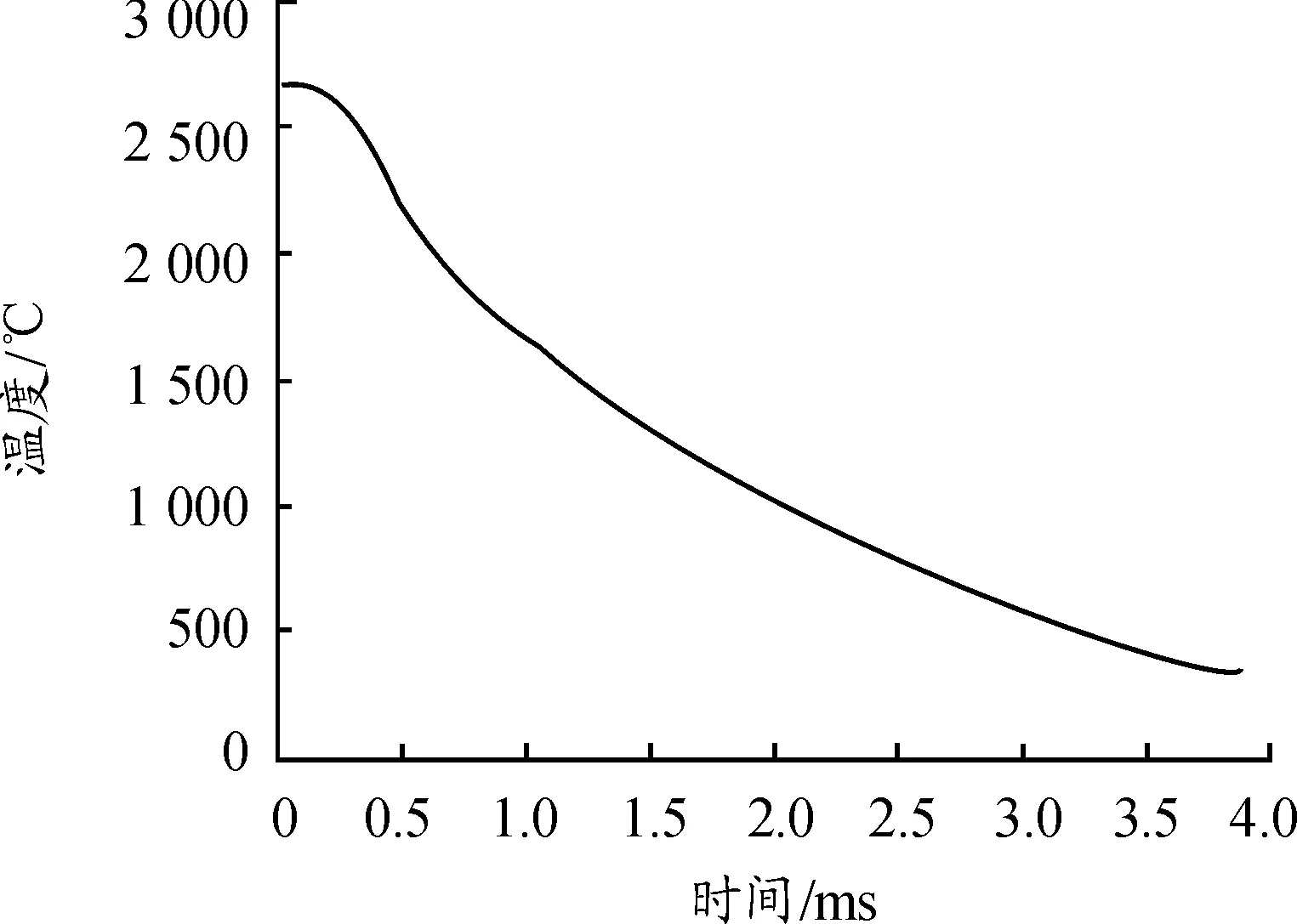
图4 火药燃气平均温度-时间曲线

火药对流放热系数曲线如图5。

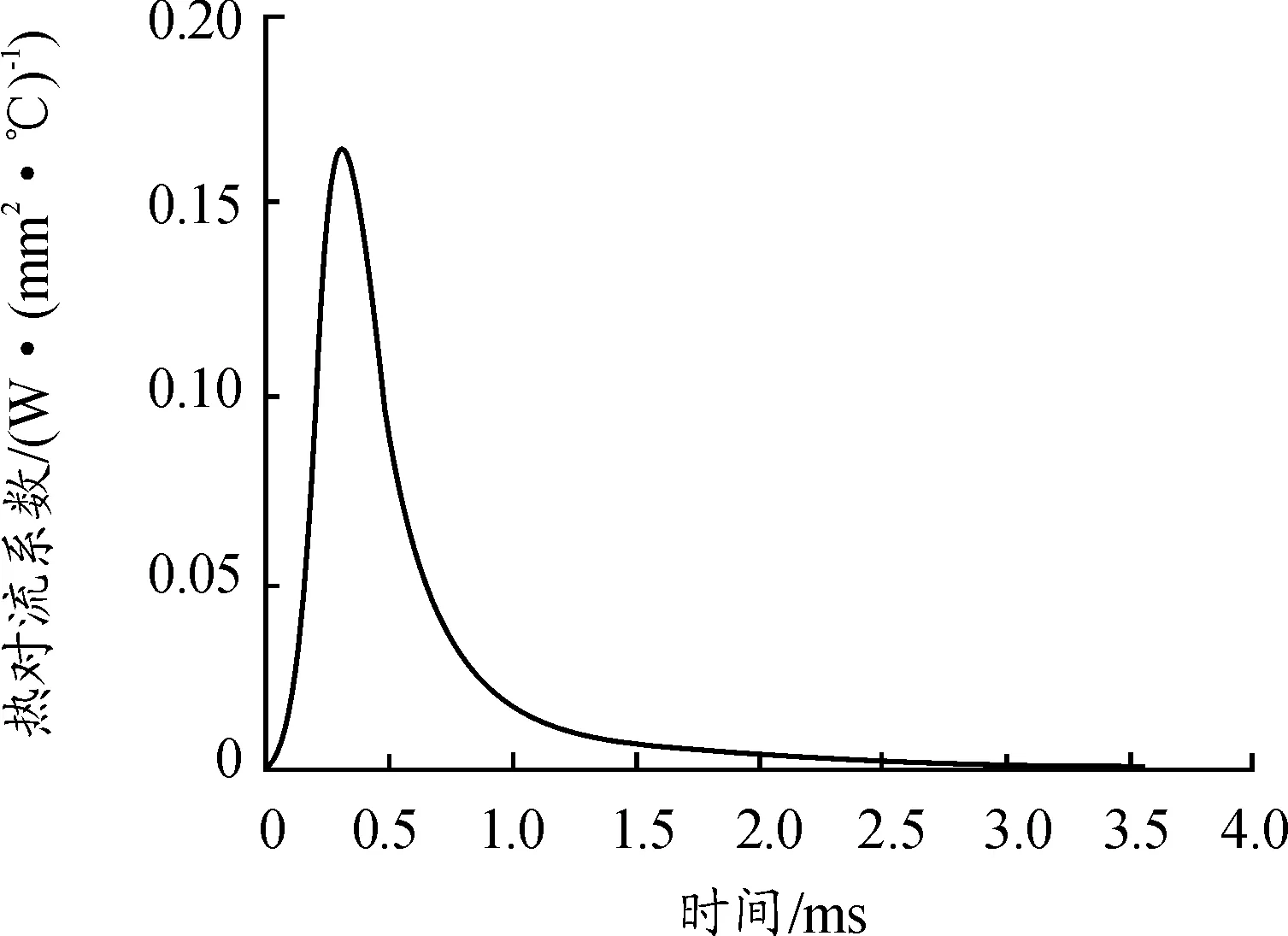
图5 火药对流放热系数曲线

3 有限元仿真结果及分析

3.1 温度场仿真结果分析

本文用ANSYS对某型机枪在高温、常温、低温条件下对单发、连发两种射弹量条件进行分析，其中单发指射弹量为1发，连发指射弹量为200发。其中连发的温度场包含了单发的温度场，因此只要仿真连发的温度场。高温选取环境温度为50 ℃，常温选取环境温度为20 ℃，低温选取环境温度为-50 ℃。温度场分析后选取典型的节点温度作为载荷条件，选取2个不同位置的典型节点进行分析，分别是外壁节点58和膛内节点22402，节点位置如图6所示。外壁节点58的位置在弹膛中间，温度场变化如图7所示。由于弹壳口部火药气体温度较高，因此选取弹膛上靠近弹壳口部的膛内节点22402，温度变化如图8所示。仿真结果显示，在环境温度越高的地方，同样的节点同样的时间，温度也越高，两者成正相关。

图6 节点位置示意图

图7 不同环境温度下200发时节点58温度变化曲线

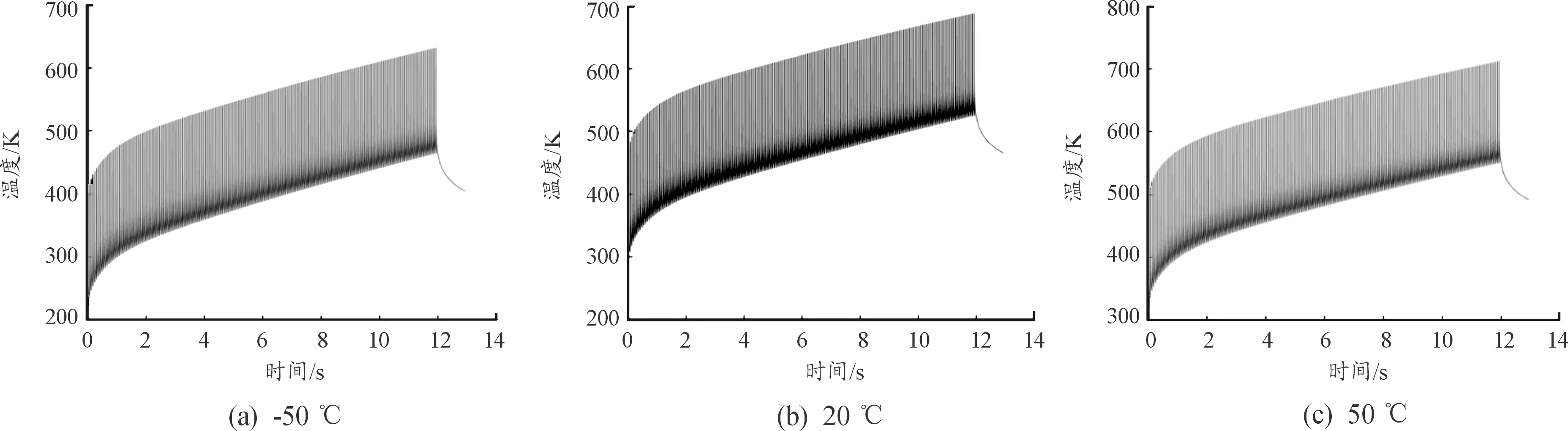
图8 不同环境温度下200发节点22402温度变化曲线

3.2 最大抽壳阻力和弹壳最大主应力分析

采用ANSYS Workbench进行热结构耦合分析，添加表面温度载荷，将温度场分析的结果条件作为载荷输入到瞬态动力学分析中。仿真得出最大抽壳阻力和弹壳最大主应力在不同环境温度和射弹量条件下的结果。选取摩擦因数作为敏感参数分析，摩擦因数的变化将直接影响抽壳阻力和弹壳最大主应力。镀铬弹膛摩擦因数约在0.05左右，沙粒附上后摩擦因数增至0.15以上，使抽壳阻力增大3倍以上。同时随着温度的不断提高，热量不容易散失，因此弹壳膨胀较大，使弹膛与弹壳间的摩擦力增加。因此对敏感参数设计一个试验参数表，观察敏感参数对最大抽壳阻力和弹壳最大主应力的影响。其中抽壳阻力变化曲线如图9，弹壳主应力分布图如图10，试验参数如表3所示。

图9 抽壳阻力变化曲线

图10 弹壳主应力分布图

表3 试验参数

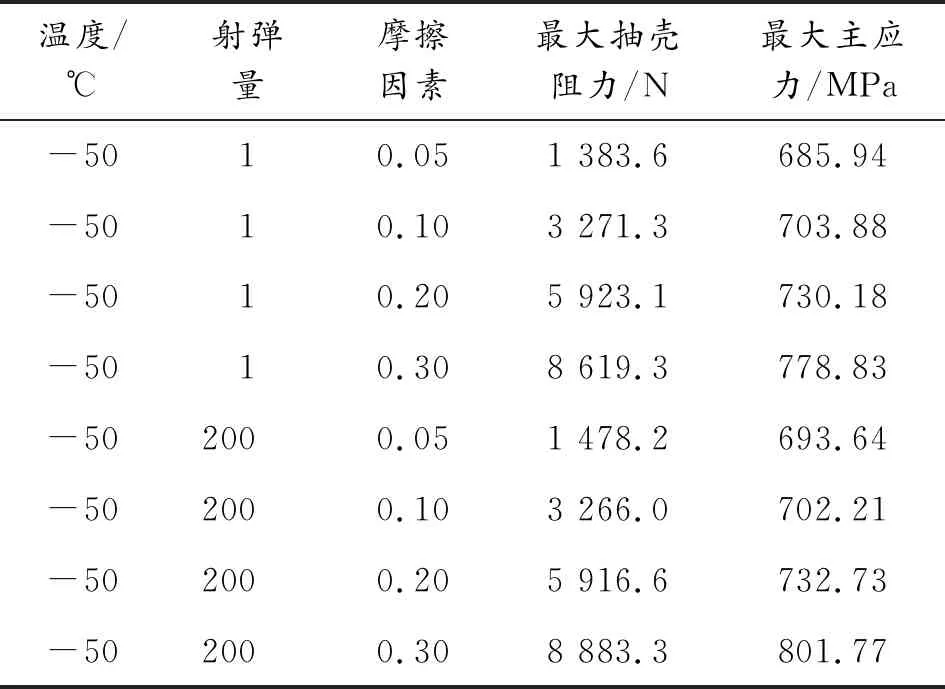
续表(表3)

通过抽壳阻力变化曲线，弹壳应力分布图，可以得出以下结论：在抽壳过程中，抽壳阻力突然增大以后，由于弹壳和枪膛脱离接触，抽壳阻力开始减小，震荡最后趋于0。弹壳最大主应力出现在弹壳的距离尾部不远处。实验参数表表明，对最大抽壳阻力和弹壳最大主应力影响最大的因素是摩擦因数，弹壳最大主应力和最大抽壳阻力总体上随着摩擦因数的增大而增大。

4 故障率分析

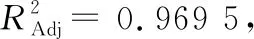
S=686.462 05+0.485 626T+0.013 388N+402.587 01f

(7)

其中：S为弹壳最大主应力；T为温度；N为射弹量;f为摩擦因数。

本文采用蒙特卡洛法模拟枪械在不同环境温度和射弹量条件下的故障率进行仿真。采用拟合后的弹壳最大主应力方程进行求解分析。考虑武器在高温、常温和低温三种环境温度和单发以及连发两种射弹量条件下工作时抽壳故障率，选取摩擦因数作为敏感参数。

通过拟合公式求解出弹壳在不同环境温度以及射弹量条件下弹壳最大主应力的均值和标准差。弹壳的硬度均值为230HV[15]，根据GB/T1172—199黑色金属硬度及强度换算可知抗拉强度约为793 MPa。采用MATLAB编写程序进行仿真，计算每种环境温度和射弹量条件下的故障率，求解结果如表4所示。其中20 ℃下摩擦因数0.05～0.23条件下单发射击时弹壳最大主应力分布如图11所示。

由表4可知，同样的射弹量和摩擦因数区间范围，温度越高，故障率也越高。同样的温度和射弹量；摩擦因数越大，故障率越高。

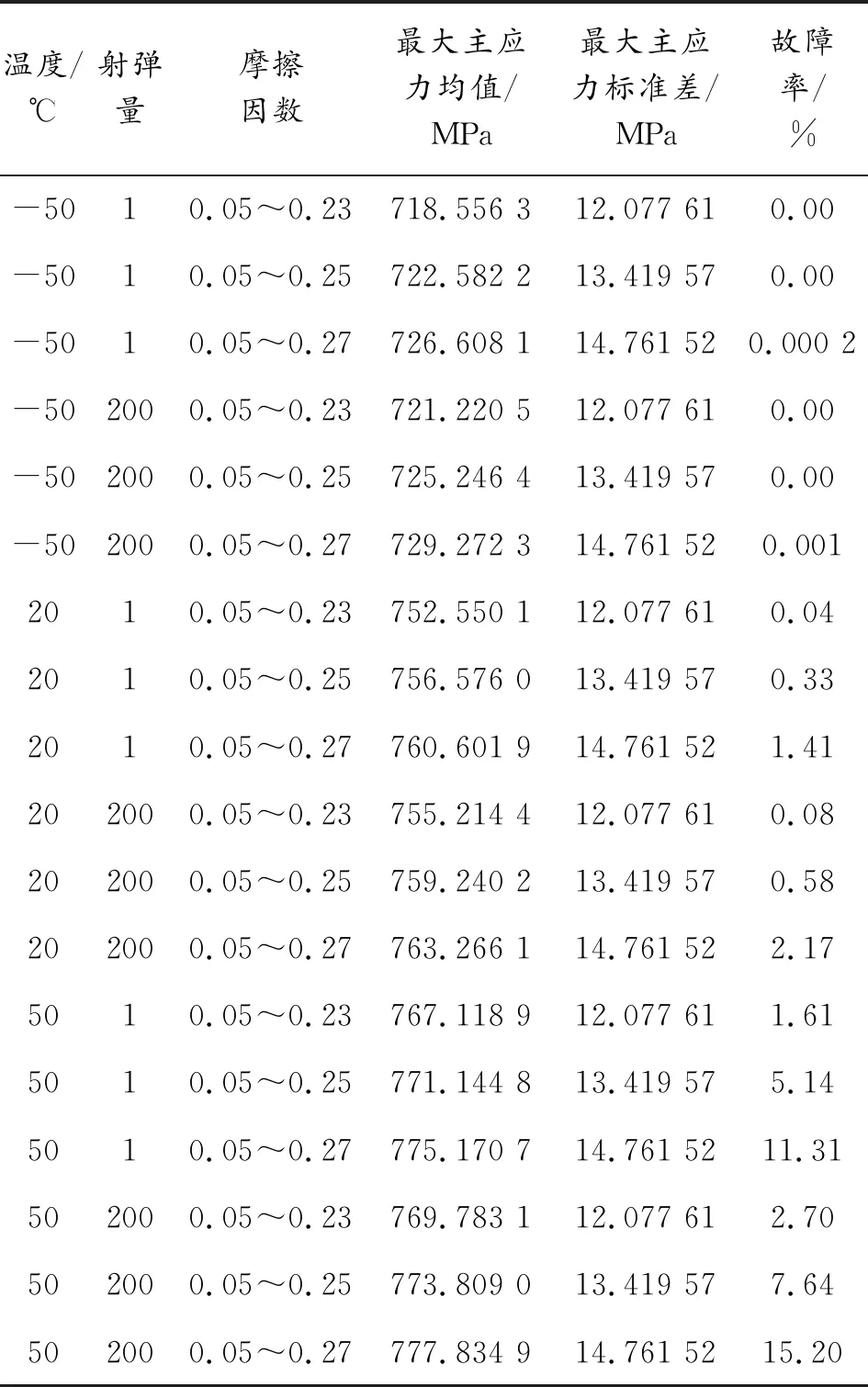
表4 不同环境温度和射弹量条件下故障率仿真结果

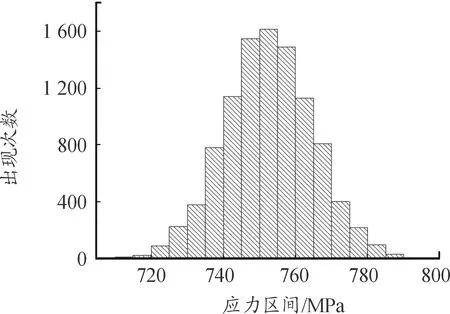
图11 弹壳最大主应力分布直方图

5 结论

通过对某机枪速射时抽壳故障的仿真研究得知：在环境温度越高的地方，同样的节点同样的时间，温度也越高，两者成正相关。最大抽壳阻力和弹壳最大主应力影响最大的因素是摩擦因数，弹壳最大主应力出现在距离弹壳尾部不远处。仿真结果表明故障率随着环境温度、射弹量以及摩擦因数的增大而增大。