计量用低速风洞结构参数仿真研究

, ,,,,

(国家海洋局南海标准计量中心，广州 510000)

0 引言

风洞是一种通过电子机械控制的产生可控气流的人造装置，20世纪40年代国外已经开始建造适合不同用处的风洞装置，迄今为止风洞的设计建造已经得到了很大的发展，风洞用途已经扩展到汽车、航空航天、新型仪器环境试验等多方面，近些年计算机信息技术的发展又极大地推动了风洞的设计，风洞的实验能力也得到了极大提高，技术的进步导致实验对风洞的性能要求越来越高，效率低、性能差的实验风洞必将被淘汰。

计量用风洞是进行风速传感器检定校准的重要辅助设备。其试验段风场特性直接关系到风速传感器的量值溯源的有效性，按照产生风速的大小，可分为低速、高速和超高速3种类型，按照设计结构可分为直流式和回流式。低速直流式风洞由于易于设计，结构简单，造价较低被广泛使用，计量用直流低速风洞其上限流速为30 m/s，它主要由稳定段、试验段、收缩段、扩散段等几部分组成[1-2]。由于其主要用于风速传感器的量值溯源，因此对试验段的流场品质有较高要求，如对试验段的风场稳定性、轴向风速梯度、法向风速分布均匀性等，都高于一般风洞。风洞风场品质的优劣与诸多因素有关，但收缩段的结构参数起着至关重要的作用。直流低速风洞收缩段的主要结构参数包括收缩段曲线参数和收缩段前后截面比，其中截面比即收缩比，关系到试验段风速大小，一般在风洞设计之初根据风洞设计的目的和使用领域已经确定，因而收缩曲线的结构参数对风洞的整体性能特别是试验段的性能参数具有极其重要意义[2-3]。目前收缩段收缩曲线主要有维托曲线、三次曲线、五次曲线，维托曲线在设计中最常用[4-5]。本文使用ansys CFD对不同的维托曲线参数下构建的风洞洞体模型进行仿真并对比分析，揭示风洞内部产生的风场运动机理，重点比较不同长度维托曲线构造的风洞模型的法向风场均匀性和轴向风速梯度，通过数据拟合，估算出最优长度参数，为计量用低速风洞洞体设计提供参考依据。

1 洞体结构及模型

1.1 风洞结构

本文研究的计量用低速风洞以现有的EDE14A2型风洞为蓝本，该风洞主要用于轻便三杯，热线风速仪等小型测风仪器的风速传感器量值溯源，该风洞壳体以玻璃钢为主要材料，风洞动力系统主要是通过电动马达带动风洞前端扇叶，使风洞前后两端产生压差，以驱动空气在洞体内流动，风洞前后两端采用圆形截面的闭口开路型形式，洞体三维模型见图1。洞体由进气段、稳定段、收缩段、试验段、扩散段等部分组成。

图1 风洞洞体三维模型

稳定段是为收缩段创造稳定的低湍流的均匀流场，它是风洞能否达到低湍流度的一个十分重要的关键部位，主要由湍流衰减装置(一般为阻尼网和蜂窝器构成)组成，蜂窝器将进气口处较大的气团打散，形成均匀分布的小型气团，再经过阻尼器将气团进一步平滑，减小其湍流度，经蜂窝器和阻尼网整流后形成较为平滑的风场，该风场通过稳定段经过收缩段加速至所需风速供试验段使用[3]，如果稳定段的性能不达要求，则进入收缩段的气流湍流度较大，流出的气流不均匀，甚至经过收缩段加速后的气流还会产生大尺度的涡旋，会严重影响试验段风场的均匀性和稳定性，稳定段的长度也会对试验段的风场产生影响，根据风洞收缩比可以估算出稳定段的最大长度，根据经验长度应该为直径的0.7倍左右。

蜂窝器的可选形状较多，有六边形、圆形、方形等结构，其中风场经过六边形蜂窝器时损失系数最小，且经过其整流风场流动的均匀性最好。阻尼网安装于蜂窝器和收缩段之间，主要作用是把经过蜂窝器的流场进一步切割，使其更为均匀，阻尼网网孔的大小根据实验为网丝直径的500倍左右，一般越小越好，但是过小风场的损失系数较大。

收缩段是风场的加速区域，其关键参数是其收缩比，该参数是收缩段入口处和出口处的横截面比值，收缩段出口处风场分布是否均匀，洞壁是否发生分离，方向是否平直且稳定，是评价其优劣的主要标准，根据风洞的不同用途选择合适的收缩比对风洞进行设计。试验段是风洞的核心部位，风速传感器一般置于此处进行测量和校准，试验段性能的好坏可以通过风洞工作效率和经过的风场品质进行评价，它的风场均匀性和风速梯度等参数是检验收缩段维托曲线参数设置是否合理的依据。

1.2 收缩曲线

在设计风洞时，风洞收缩段的收缩曲线一般要求较高，为避免气流进入收缩段产生气壁分离，收缩段的曲线函数要二阶可导，目前常用的收缩曲线主要有三次、五次方曲线、维氏曲线等三类。通过matlab绘图对上述3种曲线进行对比，维氏曲线的出口处最为平缓，与试验段过渡最为平滑，说明气流通过该种曲线设计的收缩段出口过冲较小，可以很好的保护进入试验段的流畅品质。

风洞收缩段采用维托曲线见图2。

图2 维托曲线

维托曲线公式为[6-7]：

(1)

式中，R1为收缩段入口处半径；R2为收缩段出口处半径；R为轴向距离为x处的法向距离；L为维托曲线轴向长度。

2 数值模型

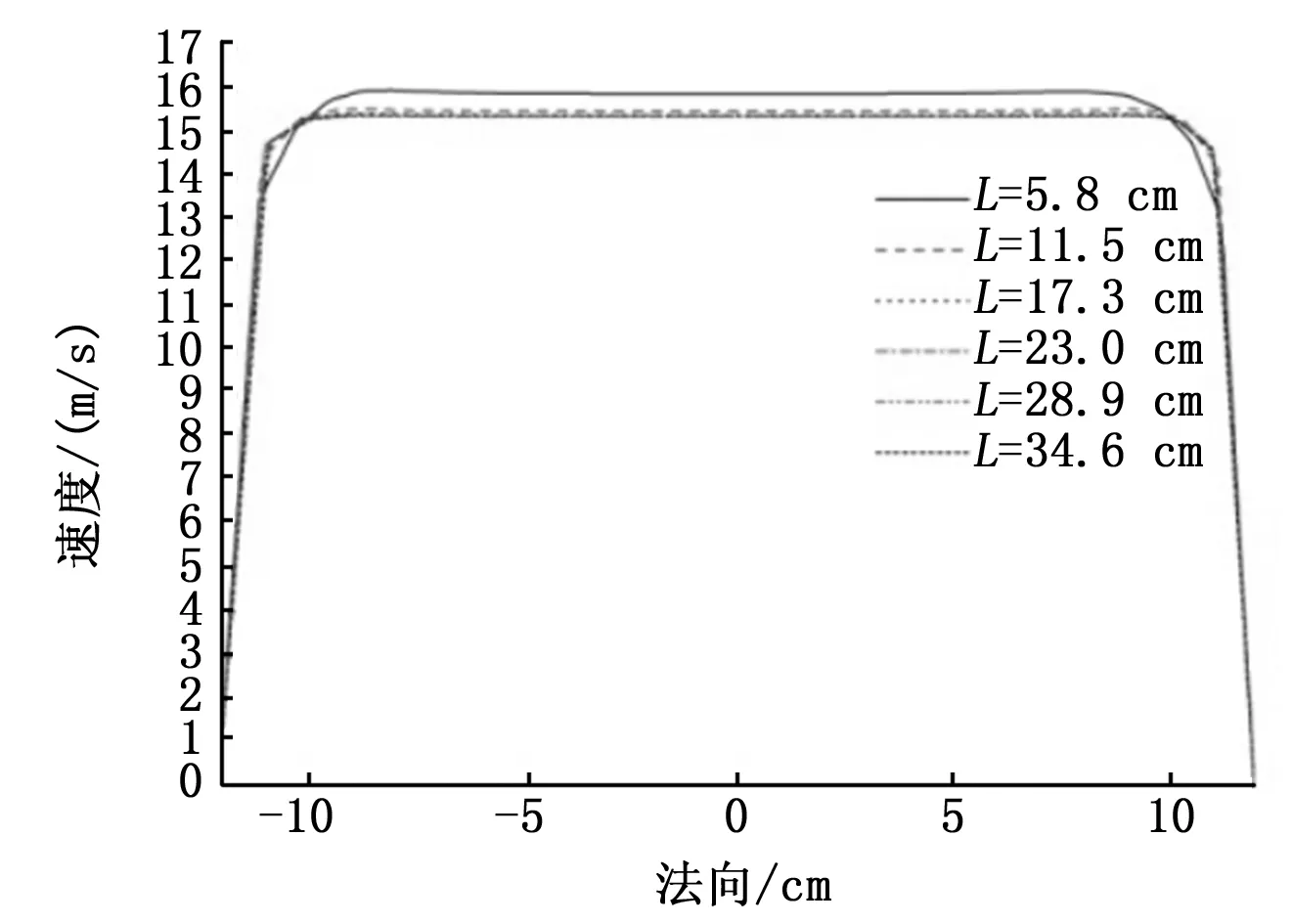
计量用低速风洞所产生的风场风速范围(0.4～30) m/s，经计算其马赫数Ma∈(0.08，0.1)，按照分类洞体内的风场属于亚声速不可压缩流。在进行数值模拟时还需考虑其雷诺数Re大小，在圆形区域，当Re≤2 300时，流场为层流；Re≥8 000～12 000时，流场为湍流；当2 300

雷诺数Re计算公式可表示为：

(2)

式中，v为流场速度；d为流场法向截面直径；ρ为流场介质密度；η为介质动力粘度系数。

经计算低速风洞风场雷诺数Re≫12 000，风洞内风场为完全湍流。不可压缩流场湍流数值模型有k-εStandard、k-εRNG和k-εRealizable三种，这3种模型都是两方程模型，其中，k-εRealizable数值模型在处理圆柱流模型时发散比率能比其它两个数值模型更准确的预测，而且它对于旋转流动、边界层流动的处理也能较为优异。

在低速流动中由于马赫数较低，为不可压缩流，在进行数值模拟时，不涉及能量传递，因此，控制方程只涉及质量和动量守恒方程[9]。

质量守恒方程：

(3)

式中，ρ是流场介质密度；t是时间，u、v、w是速度矢量在笛卡尔坐标系中x、y、z方向上的速度分量。

动量守恒方程：

(4)

k-εRealizable数值模型包括湍动能k方程和湍流耗散ε方程，湍动能k方程和k-ε Standard、k-ε RNG数值模型的k方程一样，3个数值模型主要区别在湍流耗散ε方程。

湍动能k方程：

Gk+Gb-ρε-YM+Sk

(5)

湍流耗散ε方程：

(6)

式中，Gk和Gb表示湍动能项，前者是由层流速度梯度而产生的，后者是由浮力产生的；YM表示可压缩流的耗散率，对于不可压缩流体YM=0；C1ε、C3ε是经验常数；σk和σε是k和ε的湍流普朗特数[10]。

3 仿真与分析

3.1 仿真设置

通过Solidworks绘制洞体三维模型，模型参数除收缩段参数外皆使用现有EDE14A2型风洞参数，试验段尺寸为φ24×40(cm)、稳定段尺寸为φ54×52(cm)，收缩段收缩比系数为4.7。收缩段草图使用函数驱动方式绘制，改变维托曲线长度参数L，共设定6个不同长度参数，建立6个风洞洞体三维模型，风洞洞体模型为对称模型，对称模型可扫掠，划分成6面体网格更适合做流体仿真分析，适于流场计算。网格划分选用meshing网格划分器，为便于观察风场在洞体壁面边界处的分布情况，在洞体壁面处进行加密处理，最大层数为10，增长率为1.2，收缩段和试验段的网格模型如图3所示。

图3 收缩段和试验段的网格模型

在CFD中求解器选择压力求解器，选择湍流模型k-εRealizable数值模型，入口模式为速度入口，流场进入入口方向垂直于入口边界，湍流强度根据上节数值模型计算所得修改为3.2，风场出口边界为压力出口，壁面模式设置为标准壁面，方程求解方式采用压力—速度耦合SIMPLE算法，动量方程和压力方程选用的离散方式为二阶迎风格式，残差监控参数设定值为10-3，最大计算迭代步数参数为50次。

3.2 法向速度分布

试验段内法向速度分布均匀程度是计量用风洞的重要技术指标，分布均匀表示试验段内湍流程度较小，风场较稳定，在稳定的风场中风速传感器输出测量值较稳定，可以降低由于风场稳定性引起的不确定度分量，适合风速传感器的计量溯源。

由图4～5可知：维托曲线的长度L对风场内风速的大小有一定的影响，风速大小随着长度的增加非线性递增，长度L增加到23 cm时基本稳定。

图4 试验段法向中心面速度分布云图

图5 试验段法向中心面速度

由于边界层的存在，流场在近壁面区域速度较低，但是在距离壁面一定距离后近壁面边界的流场速度变化梯度较大。目前对边界层的厚度没有统一的标准的计算公式，按照经验边界层一般取速度达到主流的99%处为边界层的外界，一般稳定的试验区在该处，在CFD Post中取试验段法向(-5，5) cm为主流区，在此区域风场的法向速度几乎无变化，以此范围的风场速度大小作为衡量边界层风场的厚度，经计算边界层的厚度约为2 cm，即可以将试验段法向(-10，10) cm作为有效法向实验区域。

将6个洞体模型试验段中心点，即x=20 cm处的法向平面内的主流区的数据抽取并计算其均匀性系数，其计算公式为：

(7)

(8)

表1 试验段法向中心面速度均匀性系

图6 试验段法向中心面速度均匀性系数

由表1和图6可知：当长度小于20 cm时风场均匀性随着长度增加减小较快，大于20 cm时随着维托曲线的长度L增加，试验段内法向中心面的速度分布均匀性逐渐增加，幅度较缓，速度均匀性系数不断减小，当维托曲线长度L增加到L>23 cm后风场均匀性系数基本处于稳定，二者呈非线性关系。

3.3 轴向速度分布

轴向速度梯度是试验段沿中心轴向速度变化的快慢，能够很好地体现试验段流场的稳定程度，它是试验段模型对气动力的直观体现，试验段内轴向速度在理想状态下应该各处相等，但由于各种因素的影响试验段轴向速度会沿着轴向逐渐减小。更进一步由于收缩段长度导致维托曲线曲率变化，使其各点变化呈现一定规律。

由图7和图8可知：对于一个确定的维托曲线长度收缩段内的轴向速度变化较快，当流场到达试验段内速度变化逐渐增加，但是比较平缓，不同维托曲线长度导致变化率各不相同，随着维托曲线长度L增加，各模型中试验段轴向风速变化率逐渐减小，在距离收缩段约20 cm处，流场速度变化较低，与轴向长度呈近似线性关系。

图7 试验段中心轴速度分布云图

图8 试验段中心轴速度

轴向速度梯度通过∂V/∂x计算所得，将图8中的试验段中心轴速度曲线在matlab中对x求偏导，将结果绘制于图9。在试验段前半段速度梯度变化较大，随维托曲线长度L的增加呈递减趋势，根据表2在约20 cm处各曲线速度梯度变化稳定，接近为0，为较稳定的风场区域。

表2 试验段中心轴x=20 cm处速度梯度

图9 试验段中心轴速度梯度

4 结束语

本文采用ansys CFD对计量用低速风洞进行了仿真研究，分析了风洞洞体收缩段曲线参数对试验段风场法向均匀性和轴向梯度的影响，得出以下结论：

1)风场法向均匀性随收缩段尺寸变化而变化，试验段法向中心面的有效试验区的均匀性系数随着收缩段长度增加而减小，到一定程度趋于稳定，本文中的风洞模型是在L>23 cm后风场均匀性系数基本处于稳定。

2)轴向速度梯度随着收缩段尺寸增加而减小，试验段前半段的风速轴向梯度明显大于后半段的风速轴向梯度，有效试验区域多集中在后半段，在本文中的风洞模型中轴向有效试验区域x>(10～15)cm。

3)本文以现有的风洞模型为蓝本，通过仿真对比了不同参数的收缩曲线对试验段风场的影响，初步估算了最佳尺寸参数，为收缩段维托曲线的设计和风洞试验段后续使 用及风速传感器检测结果的不确定度评定提供参考。