基于功率谱的风廓线雷达回波强度定标方法
李 丰 阮 征 王红艳 葛润生
(中国气象科学研究院灾害天气国家重点实验室,北京 100081)
引 言
风廓线雷达利用大气湍流对电磁波的散射作用探测大气风场等要素,能对大气垂直结构进行长时间连续观测,可以获得较高时空分辨率的廓线资料,已经成为测风的主要探测手段,在数值预报、灾害天气预警、污染监测、航空航天等领域得到广泛应用[1-9]。风廓线雷达除了获得风场数据,还可以提供强度数据,用于降水结构、类型分类、大气折射率结构等方面的研究。White等[10]使用风廓线雷达强度、速度数据对亮带高度进行识别,研究对预报效果的改进效果。Bianco等[11]基于模糊逻辑方法,使用信噪比数据对边界层高度进行分析。Lerach等[12]使用北美季风试验观测到的S波段风廓线雷达数据对降水类型进行分类,分析中尺度对流系统的垂直结构。Williams等[13]、Rao等[14]对热带地区降水结构特征进行统计。阮征等[15]使用风廓线雷达不同探测模式数据,对大气折射率结构常数进行研究。阮征等[16]和何平等[17]使用风廓线雷达产品中的速度、信噪比(signal to noise ratio,SNR)等数据对降水过程进行研究。王晓蕾等[18]进行雨滴谱反演试验,估算云中含水量,得出含水量随高度的分布。以上工作均需要对雷达返回信号功率进行准确定标。Lucas等[19]进行反演雨滴谱时,使用信噪比对回波强度进行定标。钟刘军等[20]使用信号源对雷达系统进行测量,得到不同探测模式的定标曲线,并将定标后的回波强度与天气雷达对比。王莎等[21]对风廓线雷达大气信号功率谱密度及系统噪声幅度分布特征进行统计。何平等[22]依据风廓线雷达功率谱估计方法,提出一种计算功率谱噪声功率的方法。马建立等[23]给出信噪比估算大气返回信号功率的方法,并对环境噪声进行剔除。May等[24]采用定标后的天气雷达进行比较,订正返回信号,给出强度订正大小。由于两者的取样空间及取样时间不完全一致,订正值的准确度难以保证。
目前我国业务布网风廓线雷达已超过100部,尚无可以直接使用、规范计算的返回信号强度特征数据产品,针对现有不同厂家的设备还未提出统一的定标方法。形成返回信号强度的定标曲线的方法用于现有业务雷达需要重新测量,工作量较大,且无法处理历史数据,不能有效发挥历史观测数据的作用。为解决以上问题,本文提出仅使用风廓线雷达返回信号功率谱数据的定标方法,该方法基于雷达系统噪声功率对返回信号进行定标,能同时兼顾历史数据与实时数据的处理,得到的强度产品可对现有业务产品进行有效补充。本文使用2017年北京(54399,型号CFL-03)、2016年南京(58235,型号CLC-11)和2018年梅州(59303,型号TWP8)3个不同厂家的业务布网风廓线雷达数据进行评估,并与使用信噪比定标的方法进行对比。
1 方 法
1.1 基于噪声功率的定标方法
1.1.1 功率谱数据定标
风廓线雷达探测回波信号进入接收机后,接收机将混频后的信号转换为中频信号,对中频信号进行A/D转换,形成数字中频信号送入数字中频接收机,数字中频信号分为两路混频后得到IQ(inphase and quadrature,正交两路)信号送至信号处理单元。在信号处理单元,回波信号经过相干积分、谱变换、谱平均等处理后得到功率谱数据;当无环境杂波干扰时,功率谱数据由噪声功率和大气目标信号两部分组成。风廓线雷达晴空探测时,返回信号是大气湍流引起的布拉格散射;降水出现时,返回信号由云、降水粒子的瑞利散射和大气湍流散射两部分组成。
风廓线雷达探测回波信号功率谱数据是经过信号处理后的数据,提取气象目标真实大小时需进行还原处理,才能得到真实的气象目标功率谱分布。雷达系统稳定运行时,雷达系统的噪声功率只与环境温度有关,本文提出使用雷达系统噪声功率对回波信号功率谱数据定标(data calibration with noise power,DCNP)的方法,通过噪声电平将功率谱数据分解为噪声功率谱和气象信号功率谱两部分。利用雷达系统噪声功率及噪声功率谱计算单位幅度功率大小,从探测功率谱数据中获取气象目标信号谱线分布幅度,联合单位幅度功率,计算得到真实的气象目标谱分布,进而计算风廓线雷达探测数据中与强度相关的产品。图1给出风廓线雷达功率谱数据标校计算流程图。

图1 风廓线雷达DCNP流程图
1.1.2 功率谱单位幅度功率计算
使用功率谱数据对单位幅度功率进行定标的方法是通过雷达系统噪声功率对功率谱中的噪声信号幅度进行标校计算。使用雷达噪声系数、接收机带宽等参数计算雷达系统噪声功率,将噪声功率分解到噪声谱上,计算得到功率谱分布中单位幅度的功率大小。单位幅度功率的计算公式如下:
(1)
式(1)中,PN为雷达系统的噪声功率,K是玻尔兹曼常数(取值为1.38×10-23J·K-1),T0是用绝对温度表示的雷达接收机系统噪声温度,B0为接收机的带宽,Nf为系统噪声系数,AN为雷达噪声谱分布的累积幅度,CA为单位幅度功率。
为避免外界干扰带来的影响,使用晴空时风廓线雷达每个模式最远端距离库的功率谱分布数据,用分段法[25]确定功率谱分布中的噪声电平幅度,噪声电平幅度乘以快速傅里叶变换(FFT)点数得到噪声功率的累积幅度AN。该方法可以得到功率谱每根谱线对应的功率值,进而得到回波强度功率谱密度、回波强度等产品。计算时T0取300 K。接收系统的稳定性会引起噪声幅度的涨落,为减弱其影响,AN取最远端距离库噪声幅度的月平均值。
1.1.3 功率谱强度产品
回波强度谱密度分布是从功率谱数据产生的描述回波强度在不同多普勒速度上分布的变量,使用雷达气象方程从定标后的气象信号谱分布计算得到。风廓线雷达的回波强度是回波强度谱密度的全谱积分结果,也可以看作是计算功率谱分布的零阶距。
气象信号谱分布PVi由功率谱分布中噪声电平上的信号谱计算得到:
PVi=(AVi-Af)×CA。
(2)
式(2)中,AVi是功率谱数据中速度Vi对应的信号幅度,Af为使用分段法得到的最远端距离库噪声电平幅度(量纲为1),CA为单位幅度功率。
使用云及降水的雷达气象方程计算气象信号功率谱分布,得到回波强度谱密度分布ZVi和回波强度ZDCNP(用DCNP方法得到的回波强度),单位分别为dBZ·(m·s-1)-1和dBZ:
(3)
式(3)中,C为雷达常数,Pt为发射功率,G为天线增益,θ为雷达波束宽度,Δh为库长,m为复折射指数,λ为波长,R为目标物到雷达的距离,L为馈线损耗,ΔV为功率谱数据的速度分辨率,n为FFT点数。
(4)
式(4)中,η为雷达反射率。

图2为北京风廓线雷达(54399)2017年8月22日07:05:03(世界时,下同)、南京风廓线雷达(58235)2016年7月1日01:30:00、梅州风廓线雷达(59303)2018年6月6日10:20:18使用DCNP方法定标后的回波强度谱密度。

图2 DCNP定标后的回波强度谱密度
1.2 基于信噪比的回波强度计算
使用基于信噪比的方法(reflectivity calculated with SNR,RCSNR)计算回波强度时,噪声功率乘信噪比SNR得到返回信号功率,代入雷达气象方程计算出回波强度ZSNR(基于信噪比得到的回波强度),公式如下:
ZSNR=PN·RSN·R2/C。
(5)
在无外界干扰时,RCSNR计算出的回波强度与DCNP方法基本一致。使用RSN计算回波信号功率时,会出现大气信号幅度相同,但噪声幅度不同,从而RSN不同,最后导致回波信号功率不同,即RCSNR方法会导致相同的信号幅度计算出不同的回波强度。DCNP方法先求出单位信号幅度对应的功率,再计算信号功率,保证相同的信号幅度对应的功率相同,计算出的回波强度也相同。
2 误差分析
计算回波强度用到的所有变量中,K为常数,与雷达系统有关的天线增益、波束宽度、馈线损耗等参数从谱数据中读取,对于同一部风廓线雷达,上述参数在不同探测模式中的值相同,对不同模式之间的一致性无影响,因此不对上述参数的误差进行分析,只分析噪声温度T0、噪声幅度AN带来的误差。
图3为T0取300 K时,实际噪声温度在280~320 K之间的误差分布。由图3可以看到,噪声温度取300 K,实际为280~320 K时,引起的误差范围为-0.28~0.3 dB。T0的取值对DCNP,RCSNR计算结果的准确度均产生影响,由于多个模式的取值相同,对不同模式之间的一致性不产生影响。

图3 噪声温度引起的误差范围
图4为北京风廓线雷达(54399,型号CFL-03)2017年8月、南京风廓线雷达(58235,型号CLC-11)2016年6月和梅州风廓线雷达(59303,型号TWP8)2018年6月晴空时每个模式垂直波束最远端距离库噪声幅度的小时平均值,所用数据为当月全部数据。不同雷达不同模式的噪声幅度量级差距较大,是由不同的信号处理策略引起。由图4可以看到,每个观测模式最远端距离库的噪声幅度涨落比较稳定,基本呈正态分布。梅州风廓线雷达(59303)高模式噪声幅度的分布最集中,在月平均值±0.1 dB 范围内,低模式在月平均值±0.2 dB范围内的比例为88.8%。南京风廓线雷达(58235)的低中高3个模式在平均值±0.1 dB 范围内的比例分别为89.0%,91.6% 和89.4%。北京风廓线雷达(54399)的噪声幅度在3部雷达中分布最宽,平均值±0.3 dB范围内的比例分别为88.5%,86.3%和90.7%。噪声幅度AN使用月平均值时,梅州风廓线雷达(59303)的误差一般在±0.2 dB内,南京风廓线雷达(58235)的误差基本在±0.1 dB 内,北京风廓线雷达(54399)的误差范围最大,多在±0.3 dB内。AN的取值对DCNP方法计算结果的准确度及不同模式之间的一致性均产生影响。RCSNR方法使用信噪比得到信号功率,不受AN影响。

图4 噪声幅度
3 检验评估
相同雷达不同探测模式采用不同信号处理策略,导致探测相同气象目标获取的信号强度存在差异。为评估DCNP和RCSNR两种方法,本文比较DCNP和RCSNR得到的降水云结构,同时也与风廓线雷达现有业务产品中的SNR、天气雷达强度廓线进行比较。定量评估方面,进行不同模式一致性分析,比较了DCNP和RCSNR两种方法每个模式的差异,同时也与天气雷达强度廓线对比。所有的评估均使用风廓线雷达垂直波束产品。
3部风廓线雷达分别与北京(Z9010)、南京(Z9250)、梅州(Z9753)天气雷达数据对比,风廓线雷达与天气雷达的距离分别为25.1,24.6,45.9 km。天气雷达型号均为CINRAD/SA,波束宽度为0.95°。3部天气雷达在风廓线雷达上空的垂直分辨率分别为422,406,754 m,取样体积分别约为0.14,0.13,0.45 km3。按照天气雷达在风廓线上空的垂直分辨率计算风廓线雷达的取样体积,从低模式到高模式,风廓线雷达的取样体积变化较大,分布范围分别为0.002~0.07,0.002~0.13,0.008~0.21 km3。由于风廓线雷达与天气雷达取样体积差异较大,取样时间也存在差异,两者对比只能验证定标方法是否合理,不能评估定标结果准确度。
3.1 降水云体结构特征比较
对于每个测站,分别选择1次层云降水过程进行检验。比较时,除了使用DCNP和RCSNR两种方法定标计算外,还给出风廓线雷达与强度相关的业务产品信噪比(单位:dB),以及相邻天气雷达在测站上空9个探测仰角的回波强度。降水过程分别为北京风廓线雷达(54399)的2017年8月22日 05:00—17:00、南京风廓线雷达(58235)的2016年6月30日20:00—7月1日12:00、梅州风廓线雷达(59303)的2018年6月6日06:00—24:00。3次降水过程时序图见图5~图7。其中图5a、图6a和图7a为使用DCNP方法定标计算后,进行多模式衔接处理输出的3站回波强度ZDCNP时序图;图5b、图6b和图7b为使用SNR方法得到的回波强度ZSNR时序图;图5c、图6c和图7c为风廓线雷达业务产品中的垂直波束SNR时序图,图中已经过距离订正[11];图5d、图6d和图7d为与3部风廓线雷达相邻天气雷达提取的测站上空9个扫描仰角数据插值输出结果。
图5c显示北京风廓线雷达(54399)个例中的业务SNR产品在融化层无明显亮带特征,且分布不连续,降水结构不清晰。图6c南京风廓线雷达(58235)降水过程中的SNR产品中尽管可以看到融化层的结构特征,但在3.2 km高度出现明显的不同模式衔接引起的不连续,下部强度明显大于上部,与实际的降水结构不一致。图7c梅州风廓线雷达(59303)个例中的SNR在5 km高度出现两层距离较近的亮带特征,且低层强度大于高层,云体的强度特征描述失真。图5c、图6c、图7c中的风廓线雷达业务SNR产品呈现的云体结构特征差异很大,不同模式之间存在衔接的连续性问题,表明不同型号雷达的信号处理策略不同,产品生成算法也存在差异,因此无法有效使用此产品进行降水云体的结构特征分析。
图5a、图6a、图7a中DCNP方法计算的风廓线雷达回波强度与图5d、图6d、图7d中的天气雷达廓线强度相近,反映的降水结构相似。图5a与图5d在05:00—08:00呈现亮带特征,09:00—13:00为整个过程中回波较弱时段。天气雷达廓线无数据的空白区域与风廓线雷达弱回波区相对应。图6a、图6d中的强回波出现时间基本一致,高度也相近。图6a中7月1日02:30—04:00,05:00—06:00,08:50—09:40为低层回波较弱阶段,图6d中的天气雷达廓线与之对应较好。图7a与图7d中的强度较强时段及较弱时段均吻合较好。图7d中天气雷达廓线在17:15—19:08出现大片空白无回波区域,图7a中的弱回波区与之对应时间较好。

图5 北京风廓线雷达(54399)观测的2017年8月22日 05:00—17:00降水过程与天气雷达对比

图6 南京风廓线雷达(58235)观测的2016年6月30日 20:00—7月1日12:00降水过程与天气雷达对比

图7 梅州风廓线雷达(59303)观测的2018年6月6日06:00—24:00降水过程与天气雷达对比
总体上,DCNP计算的回波强度与相邻天气雷达提取的测站上空廓线产品的回波强度变化趋势基本一致。风廓线雷达的垂直分辨率优于天气雷达,得到的云体结构特征更清晰,能够为降水云垂直精细结构及垂直演变特征的研究提供更细致的数据支持。
图6b、图7b中RCSNR方法计算的回波强度变化趋势与DCNP方法一致,强度略低于DCNP方法。图5b中RCSNR方法计算的回波强度在5 km附近存在明显的不连续,原因见3.4节。
3.2 多模式探测的一致性检验
为定量评估DCNP,RCSNR两种方法对不同探测模式的定标结果差异,对比不同探测模式探测重叠高度范围内的回波强度数据,使用的样本数据强度在15 dBZ以上。图8为DCNP,RCSNR两种方法得到的3部风廓线雷达不同模式强度散点图。图8中虚线由用于对比的两种模式回波强度拟合得到。考虑到不同模式探测空间和时间的差异以及每个模式自身的定标误差,可以认为同一部风廓线雷达的不同模式定标结果具有较好一致性。从DCNP方法计算结果可知,梅州风廓线雷达(59303)高低模式的一致性最好,北京风廓线雷达(54399)不同模式之间的差异比梅州和南京略大。噪声分布宽度也是梅州风廓线雷达(59303)最窄,北京风廓线雷达(54399)最宽(图4)。不同模式的一致性与噪声幅度稳定度相关联,即噪声幅度涨落范围窄的雷达多模式一致性较好。

图8 DCNP,RCSNR方法得到的同一风廓线雷达不同模式一致性对比
从RCSNR方法计算结果可知,图8中RCSNR方法的南京风廓线雷达(58235)中低模式一致性略好于DCNP方法,其他模式的一致性均低于DCNP方法,特别是北京风廓线雷达(54399)的中低、高中模式一致性明显低于DCNP方法。DCNP方法的模式一致性整体好于RCSNR方法。
3.3 与天气雷达的一致性检验
为定量评估风廓线雷达功率谱定标计算结果,将DCNP,RCSNR方法计算的风廓线雷达强度与天气雷达廓线数据进行对比。数据使用图5~图7的3次降水过程全部时段内的廓线数据,样本的回波强度均在15 dBZ以上。对比使用风廓线雷达多模式拼接后的数据,并将风廓线回波强度在天气雷达某个仰角对应高度范围内的数据平均,结果见图9。

图9 风廓线雷达定标结果与天气雷达对比
考虑到风廓线雷达与天气雷达观测时间难以保持一致,两者扫描角度、取样空间差异较大,可以认为DCNP方法计算的风廓线雷达回波强度与天气雷达有较好一致性。对同一部风廓线雷达,DCNP方法的一致性略好于RCSNR方法。对于不同的定标方法,梅州风廓线雷达(59303)与天气雷达一致性最好,北京风廓线雷达(54399)的一致性相对较差。北京风廓线雷达(54399)与天气雷达一致性比另两部风廓线雷达差可能由以下原因引起:一是北京风廓线雷达(54399)的远端距离库噪声分布宽度大于另两部雷达,接收系统的稳定性不如另两部雷达,计算得到的平均值用于定标时带来的误差略大,北京风廓线雷达(54399)多模式一致性不如另两部雷达也由该原因引起。另一个原因是北京风廓线雷达(54399)与天气雷达比较的样本量仅为另两部雷达的60%,会对代表性造成一定影响。
3.4 DCNP与RCSNR方法对比
为定量比较DCNP与RCSNR两种方法,将3部风廓线雷达每个模式使用两种方法得到的数据进行对比,用于对比的样本回波强度均在15 dBZ以上(图10)。大部分情况下两种方法的结果基本一致。对于南京风廓线雷达(58235)中模式、梅州风廓线雷达(59303)低模式,DCNP方法的强度一般要高于RCSNR方法,特别是30 dBZ以上的数据。两种方法计算的北京风廓线雷达(54399)中模式数据差异较大,RCSNR方法计算的强度明显小于DCNP方法,有的差异达到10 dB以上。为分析两种方法结果差异的原因,计算风廓线雷达不同模式每个高度上由分段法得到的噪声幅度平均值(图11)。
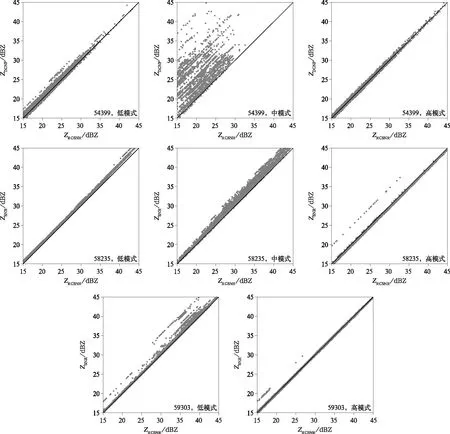
图10 DCNP与RCSNR方法不同模式对比
由图11可以看到,北京风廓线雷达(54399)、南京风廓线雷达(58235)的中模式噪声幅度随高度不断变化,最大幅度在10 dB以上。北京风廓线雷达(54399)的中模式远端噪声幅度较大,引起SNR降低,使RCSNR方法的计算结果明显低于DCNP方法。由图11还可以看到,融化层高度附近,3部风廓线雷达的噪声幅度均明显升高,变化幅度最大可达15 dB以上,北京风廓线雷达(54399)的中模式远端距离库正好在亮带附近。风廓线雷达融化层附近噪声幅度升高的原因还需要进一步分析。

图11 降水过程噪声幅度值平均值随高度的分布
3.5 湍流散射对定标的影响
降水时,风廓线雷达探测返回信号除了降水粒子散射,也含有大气湍流散射。对于UHF(ultra high frequency,超高频)波段,降水强度达到中雨以上时,1.5 km高度以上返回信号基本由降水粒子散射引起[19,26]。本文使用的3个个例时段累积降水量分别为13.6,50.3,72.5 mm,降水强度均在中雨以上。
梅州风廓线雷达(59303)个例部分时段功率谱数据在1.5 km以下出现双峰结构。对于L波段雷达,降水强度在中雨以上时,准确分离湍流谱与降水粒子谱比较困难[26-27],本文使用0 m·s-1作为分界,将出现双峰的功率谱简单分为湍流散射区与降水粒子区,用于定性分析湍流、降水粒子散射信号的强度差异。图12为双峰谱中湍流散射、降水粒子散射强度对比。Zair为湍流区强度,Zrain为降水粒子区强度,Z为使用式(3)全谱积分得到的回波强度。Zair相对于Zrain的占比最大为10%,平均为1.8%。对于图12使用的谱数据,湍流区对应的强度基本可以忽略,由图12中也可以看到,降水粒子区的强度与全谱积分的强度基本一致。此外,湍流区中也可能存在小粒径降水粒子引起的散射[27-28],湍流散射形成的回波强度会更小。因此,对于本文个例,湍流散射形成的返回信号可以忽略。

图12 双峰谱湍流区与降水回波强度对比
4 小 结
不同厂家对风廓线雷达信号处理算法不同,业务产品中的强度产品不能有效反映降水云体结构,本文提出基于雷达系统噪声功率的风廓线雷达功率谱数据定标方法(DCNP),使用我国业务布网的3种主要型号测站数据对该算法评估分析,与SNR定标方法进行比较,并使用相邻天气雷达进行定标结果准确性检验,形成以下结论:
1)风廓线雷达返回信号强度定标,使得风廓线雷达除了输出测风产品外,对返回信号强度的处理算法可以增加回波强度谱密度分布、回波强度、大气折射率结构常数3种强度产品。
2)使用雷达系统噪声功率对返回信号谱单位幅度进行标校,可保持相同探测雷达系统不同探测模式间信号处理的数据一致性;同时也解决了采用不同信号处理策略的不同型号业务雷达多探测模式数据的衔接问题。
3)DCNP方法计算的回波强度不同模式的一致性较好,与天气雷达数据也有较好的一致性,定标方法合理。
4)与SNR定标方法相比,DCNP方法受异常噪声电平的影响较小,计算结果更为稳定可靠。


