考虑学习效应的单人作业车间多目标调度算法
胡金昌,刘紫薇,马文凯,吴耀华
(山东大学 控制科学与工程学院,山东 济南 250061)
0 引言
学习效应[1]是生产中常见的现象,只要有人工参与的生产活动几乎都存在学习效应。随着对工艺熟悉程度的增加,工人的操作越来越熟练,操作时间随之减少。半自动机床只需人工上料和下料操作便可以自动化加工,无需看守,因此管理者通常安排一个工人监管多台机床。这样的加工模式提高了工人操作机器的频率,从而增大了学习效应的影响。Biskup[2]和Cheng等[3]最早将学习效应应用于排序问题;Kuo等[4]提出依赖加工时间和的学习效应模型,即工人实践的时间越长,表现越好,该模型被大量应用于单机、平行机、流水车间等调度问题;Wu等[5]研究了基于依赖加工时间和的学习效应的多机订单调度问题,以最小化误工时间;Wu等[6]在单机调度问题中考虑截断的基于依赖加工时间和的学习效应与基于前期工件加工顺序的配送时间;Rudek[7]研究了平行机调度问题,以最小化最大完工时间,其工件加工时间应用一般性基于加工时间和的数学模型,该模型适用于学习效应和衰退效应;Zou等[8]研究了两阶段3台机器的装配车间调度问题,不同机器的工件加工时间受依赖不同机器加工时间和的学习效应的影响;Mousavi等[9]分析了安装时间和加工时间均受学习效应影响的流水车间调度模型;Tayebi Araghi等[10]在作业车间调度问题研究中考虑了受学习效应影响的安装时间和受恶化效应影响的工件加工时间;Heizer等[11]指出不同产品的学习率在70%~90%之间,这意味着后一个生产单位的加工时间是前一个的70%~90%,同种工件的加工时间因为顺序不同存在明显差异,所以考虑学习效应的调度系统必然会提高调度的准确性。
因为为单人操作多台机器,工人行走于各个机器之间的耗时较长,如果工人频繁、反复穿梭于各个机器间,会影响其热情和工作满意度,所以考虑工人的行走路径也具有一定必要性。现有车间调度研究考虑了最短行走路径因素,例如Nip等[12]研究了流水线车间调度和最短路径组合问题,目的是最小化行走路径和加工总时间,并提出了近似算法;Range等[13]解决了考虑行走路径的多分类多机器且机器加工能力有限的车间调度问题;刘凯等[14]讨论了工人作业时间随机分布且与工人行走路径时间相互独立的U型线平衡问题。与工人行走类似,部分研究人员考虑了工件的运输时间,Zhang等[15]提出改进的遗传算法解决考虑机器之间工件运输时间的柔性作业车间调度问题;Karimi等[16]针对考虑运输时间的柔性作业车间调度模型,构建了两种混合整数规划模型,提出混合帝国主义竞争算法解决大规模问题;Jiang等[17]研究了一种由输送带运输的考虑运输时间的流水车间调度问题;轩华等[18]研究了可重入混合流水车间调度,运输时间指工件不同加工阶段之间的运输时间。上述研究中的运输指同一个工件的不同工序在不同机器之间的运输,与此不同,本文单人作业场景的运输时间为由加工工件变化带来的加工机器转换的耗时,这使行走时间和最大完工时间成为一对相悖的目标。例如,工人如果选择加工完一台机器的所有工件后再加工另一台机器的工件,则行走时间较短,但等待机器的时间较长,其他机器的利用率较低,最大完工时间增加。因此,有必要在调度时平衡工人行走时间和加工效率的关系。
由于考虑了学习效应,本文目标值的计算复杂度会增加。计算目标值时间的增加影响了算法迭代次数,导致求解效果下降,因此提高算法的邻域搜索能力成为求解本文问题的重点。另外,考虑学习效应和运输时间的单人单工序作业车间的多目标调度问题,目前尚未有合适的算法直接求解。作为解决多目标问题的经典启发式算法,带精英策略的快速非支配排序遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm,NSGA-Ⅱ)的结构简单、适用性强,很多多目标车间调度问题在其基础上进行改进,例如吴秀丽等[19]考虑问题特性设计了降准解码算法;朱伟[20]改进染色体编码,采用了线性次序交叉和逆序变异的方法;Wang等[21]结合启发式算法提高搜索能力;Sheikhalishahi等[22]建立了考虑工人犯错和预防性维护的最优化工人犯错率、机器利用率和总加工时间调度模型,通过实验证明相对于多目标粒子群优化(Multi-Objective Particle Swarm Optimization,MOPSO)算法和增强Pareto进化算法(Strength Pareto Evolutionary Algorithm-Ⅱ,SPEA-Ⅱ),NSGA-Ⅱ的优化效果更优;Ahmadi等[23]解决了最优化总加工时间和稳定性的柔性车间调度问题,通过实验证明了NSGA-Ⅱ在多个指标下的有效性。这些基于NSGA-Ⅱ设计的算法对解决文本问题提供了参考。另外,迭代Pareto贪婪算法(Iterated Pareto Greedy algorithm,IPG)可以有效提高邻域搜索能力,在解决流水车间多目标问题上应用广泛,如文献[24-27]等,其主要思想是在解集中选择某一解,提取该解中多个工件,剩余的工件可视为子序列,然后逐个插入提取的工件。因为每个工件可以插入子序列中的不同位置,所以每次插入工件会生成多个子序列,保留其中不被支配的子序列,直到所有工件完成插入,该过程可以有效搜索解的邻域,被称为解构和重构。然而,当这种方法所选择解构的解的数量或每个解中所提取工件的数量较多时,会使目标值的计算次数激增,迭代次数减少,从而影响搜索效果;当数量较小时不能有效扩展解空间,也会影响搜索效果。因此,传统的IPG很难直接求解本文问题。
本文针对考虑学习效应的单人作业车间多目标调度问题,提出考虑学习效应的多目标贪婪算法,融合NSGA-Ⅱ与基于贪婪的邻域搜索,构造了迭代多目标遗传算法(Iterated Multi-Objective Genetic Algorithm, IMOGA),并通过仿真实验证明了该算法解决本文问题的有效性。
1 问题描述与建模

定义如下决策变量和辅助变量:
zki为决策变量,zki=1表示第k个工件在机器i上加工,否则zki=0。
xki为辅助变量,表示准备安装第k个工件时在机器i可以安装的最早时间。
构建如下数学模型:
f1=minCmax;
(1)
f2=minD。
(2)
s.t.
(3)
(4)
xki≥0,i=1,2,…,M;k=1,2,…,N;
(5)
i=1,2,…,M,k=2,3,…,N;
(6)
V(1-zkiz(k-1)l),i=1,2,…,M,
l=1,2,…,M,i≠l,k=2,3,…,N;
(7)
i=1,2,…,M,k=1,2,…,N;
(8)
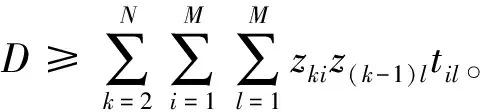
(9)
其中:式(1)表示目标1,即最小化最大完工时间;式(2)表示目标2,即最小化行走时间;式(3)限制每个工件只能被加工一次;式(4)限制每个机器只能加工相应数量的工件;式(5)限制每个工件只能在零时刻之后被安装;式(6)限制第k个工件的加工机器的允许安装时间,对于所有机器,准备安装第k个工件时,机器i可以安装的时间一定大于或等于准备安装第k-1个工件时机器i可以安装的时间,如果第k个工件的加工机器与第k-1个工件相同,则需要第k-1个工件安装并加工完成后才允许安装第i个工件;式(7)限制了机器的安装只能发生在工人到达该机器之后,即xki大于等于工人完成第k-1个工件安装后到达第k个工件加工机器的时间,其中V为足够大的数,其使zkiz(k-1)l=0时式(7)变为无效条件;式(8)限制最大完工时间应在所有工件加工完成后;式(9)定义了行走时间的计算方式。
该模型和传统的车间调度问题模型不同,对比文献[28]对传统模型的分析,本文模型呈现以下特点:
(2)本文考虑了两机器之间工人的行走时间,该变量需要通过决策变量确定机器的先后顺序,因此第k和第k-1个工件加工机器之间的工人行走时间表示为zkiz(k-1)ltil,使模型中增加了二次不等式约束,即式(7)。
(3)单人操作和工件为单工序的前提,决定了本文需要依次确定各个工件的加工机器,因此定义了决策变量zki和辅助变量xki,其数量均为MN,约束条件的数量为N+M+3MN+M(M-1)(N-1)+1。
鉴于此,该数学模型不易求解,本文提出考虑学习效应的贪婪算法和IMOGA。
2 考虑学习效应的多目标贪婪算法
2.1 目标计算方式

Ck(π)=Ok(π)+pπk;
(10)
(11)
(12)
(13)
(14)
2.2 考虑学习效应的多目标贪婪算法
传统贪婪算法的思想是按一定规则选择未插入调度列表的工件,将其插入调度列表,使插入之后的列表符合某最优条件,例如NEH(M.Nawaz, E.E.Enscore, I.Ham)启发式算法需要保证最大完工时间最小[24-27],这些传统贪婪算法一般只能对单一目标求解。对于本文的多目标问题,传统贪婪算法不能实现求解的广泛性和均匀性,因此本文提出考虑学习效应的多目标贪婪算法(Multi-Objective Greedy algorithm with Learning effect, MOGL)。MOGL的基本思想是分配一部分工件,以最小化完工时间作为插入位置的判断准则,另一部分工件以最小化工人行走时长作为插入位置的判断准则,通过变化分配的比例调节两个目标的贪婪程度,从而获得多个贪婪解。该比例用r表示,前rN个工件插入时以最小化最大完工时间作为插入位置的判断准则,剩余工件以最小化工人行走时长作为插入位置的判断准则,每个解生成方式如下:
步骤1随机选择某一工件放入调度列表,生成仅包含一个工件的初始列表,执行步骤2。
步骤2若调度列表中的工件数量N′=N,则该解生成结束;若N′>rN,则转步骤4;否则执行步骤3。
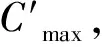
步骤4随机选择一个剩余工件,计算其插入列表的首位、末位和任意两工件之间时新列表的D′,插入使D′最小的位置,返回步骤2。
r的取值越丰富、越均匀,解集的广泛性越好。因此构造多个解时,只要调节r的取值,利用上述方式求解,便可得到对两个目标不同贪婪程度的解集。
3 迭代多目标遗传算法
传统的非支配排序遗传算法(Nondominated Sorting Genetic Algorithm, NSGA)由Srinivas和Deb于1994年提出[29],其进一步改进算法,提出了NSGA-Ⅱ,以及非支配解排序方法、精英选择策略和拥挤度计算方法。本文针对单人作业车间调度问题,定义了NSGA-Ⅱ的编码和变异方法。交叉的操作效果和变异差别不大,为降低算法复杂度,在生成新种群时删除了交叉操作。NSGA-Ⅱ是IMOGA迭代中的一部分,起随机扰动的作用,在完成NSGA-Ⅱ后,IMOGA增加了基于贪婪的邻域搜索来优化寻优效果。迭代前,本文采用MOGL构造初始解集。
(1)染色体编码
本文NSGA-Ⅱ染色体为所有工件排列成的有序数组,每个工件代表一个基因。例如{1,1…,2,2,…,M,M,…}为一条染色体,每条染色体均为该问题的可行解,如图1所示。
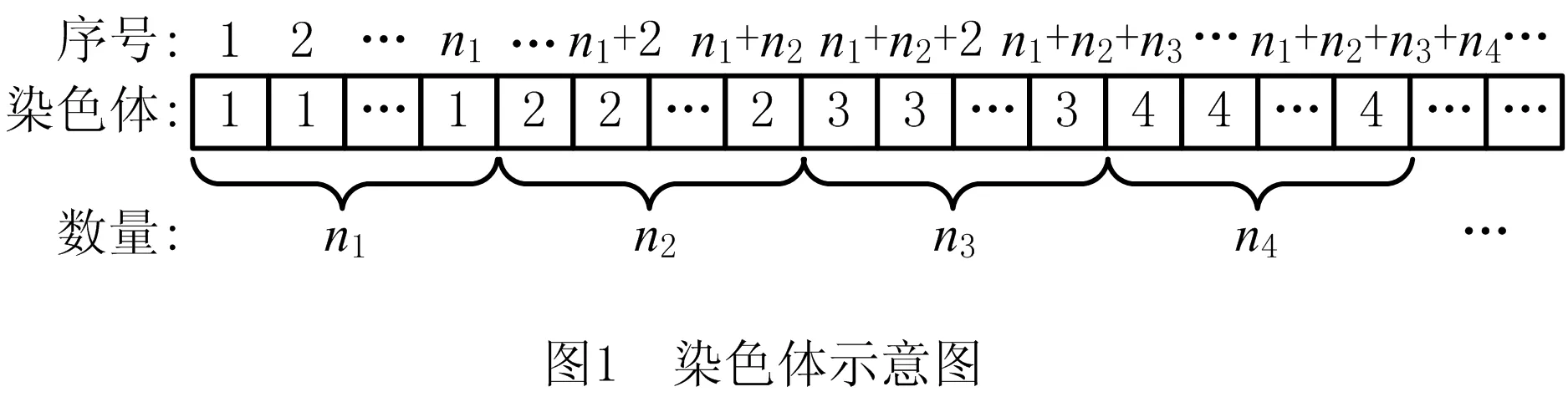
(2)初始种群
初始种群对算法效果的影响较大,传统的NSGA-Ⅱ采用随机方式或启发式算法构建初始解。对于传统IPG,有的以随机方式产生初始解,如文献[25];有的采用贪婪算法构建针对单目标的初始解,下文称这样的解为极端解,例如文献[24,27]采用启发式算法求极端解,文献[26]采用NEH和随机的方式构建初始解集。
本文构建通用型MOGL来获得多样性的初始解,参数r=1时,MOGL可以获得最小完工时间的极端解,此时MOGL改变了传统NEH启发式算法选择工件的方法,使其更适应单人作业场景;参数r=0时,MOGL可以获得最小化行走时间的极端解;r取其他值可以得到两个目标不同贪婪程度的解。本文利用MOGL的灵活性设计了生成初始种群的方法,并通过实验测试了不同初始解集对IMOGA的影响。
(3)变异
变异是随机选择两个不相同的工件,交换其位置,该方式在算法优化前期起迅速扩展解空间的作用,后期对解集进行随机扰动,以辅助解集跳出局部最优。多数传统IPG[24-25,27]没有随机扰动操作,只在加工序列解构和重构过程中扩展解空间,其搜索邻域的范围不够充分,本文弥补了此项不足。
(4)基于贪婪的邻域搜索
经典IPG[24-27]是利用一定规则在解集中选取一解,然后在该解中提取多个工件,依次插入剩余加工序列的两两工件之间,并在插入每个工件时保留非支配解。对于本文问题,如果提取多个工件依次插入两两工件之间,则计算量大,较为耗时。因此本文进行了改进,每次仅提取一个工件,然后对每一个非支配解执行多次工件提取后插入的操作,使每个非支配解的邻域均可被搜索,从而提高了搜索的有效性和广泛性,并节省了搜索时间,增加了算法迭代次数。另外,本文的邻域搜索部分增加了快速非支配解排序、计算拥挤度、精英选择策略,从而有效保留了每次邻域搜索中得到的优质解。每个染色体提取插入操作的次数用参数w表示,假设当前解集为Pg,染色体数量为|Pg|,则邻域搜索算法步骤如下:
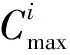
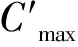
步骤3对Pg∪Qg中的所有解进行快速非支配解排序,并计算拥挤度,同时根据精英选择策略保留|Pg|个染色体代替当前种群Pg,邻域搜索结束。
(5)终止条件
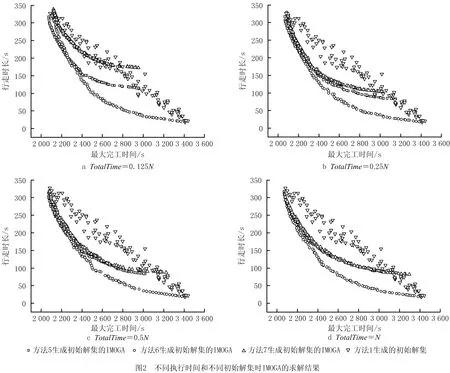
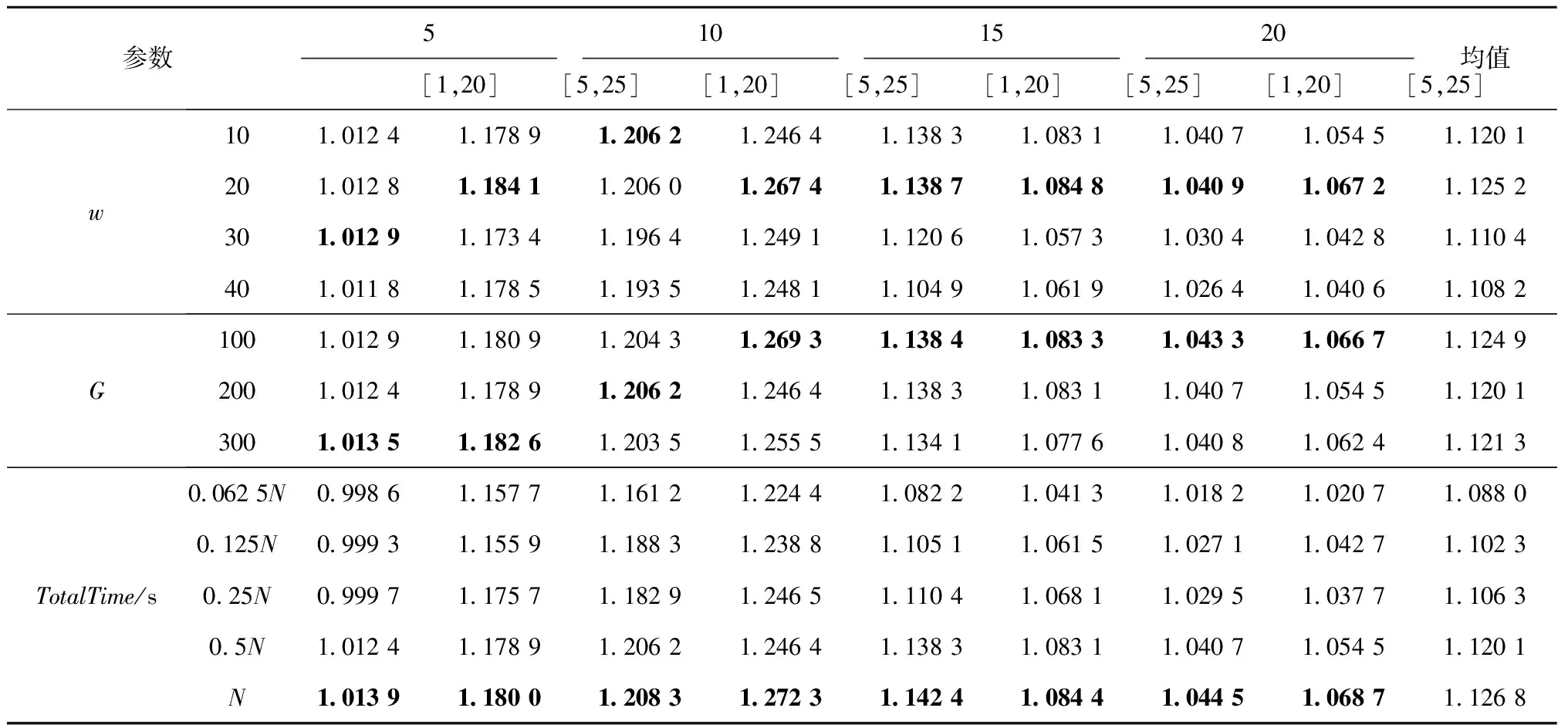
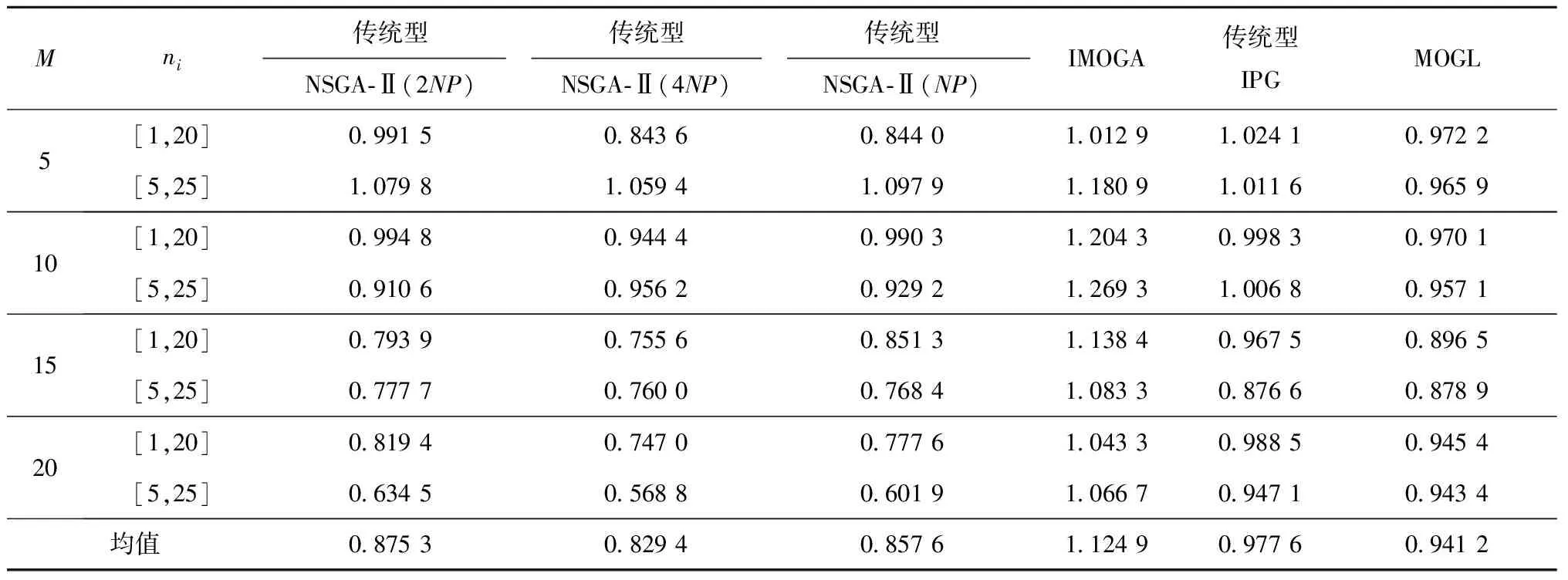
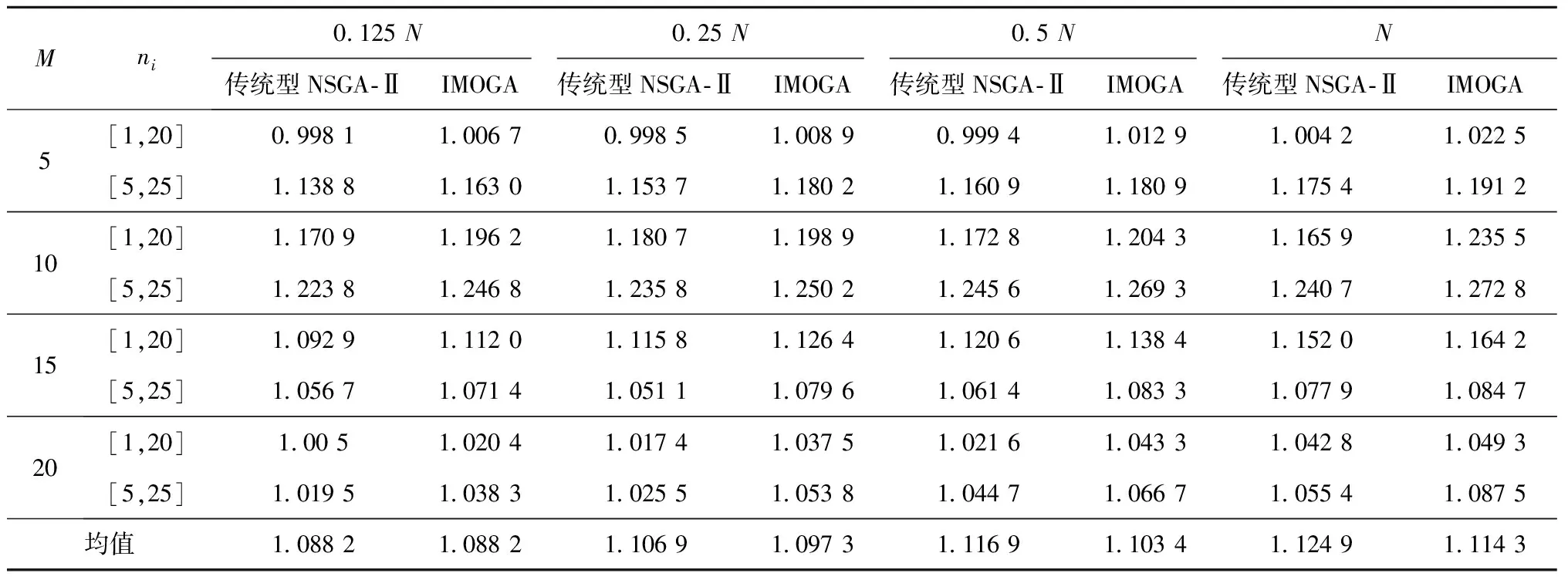
算法设置两种迭代的终止条件,一是到达迭代次数阈值,即L (6)IMOGA主流程 步骤1初始化染色体数NP、初始种群Pg、每次迭代中NSGA-Ⅱ世代数上限G、参数Lend和w,令迭代次数L=0。 步骤2检测是否达到终止条件,如果达到终止条件,则算法终止,输出HL;否则,令L=L+1,g=1,执行步骤3。 步骤3如果g≤G,则执行步骤4;否则,执行步骤6。 步骤4在种群Pg中随机选择两条染色体进行变异,将生成的两条新染色体填充至Pg。循环步骤4,直到Pg中包含3NP条染色体后执行步骤5。 步骤5计算Pg中所有染色体的目标值,对目标值相同的染色体去重后进行快速非支配解排序,并计算拥挤度。根据精英选择策略,保留NP条染色体,生成Pg+1,g=g+1。返回步骤3。 步骤6对Pg进行基于贪婪的邻域搜索,更新Pg,HL=Pg,返回步骤2。 快速非支配解排序、计算拥挤度、精英选择策略可参考相关文献,本文不再赘述。 综上所述,IMOGA在传统NSGA-Ⅱ解决多目标问题优势的基础上,融合了迭代贪婪算法的思想,可以有效提高精英解的质量并保留到下一代;IMOGA利用MOGL产生初始解集,突破了传统贪婪算法只能对单一目标求解的局限性,不但可以求得各个目标较优的极端解,而且使其能够适应考虑学习效应的加工环境;基于贪婪的邻域搜索考虑本文在计算目标值方面耗时较长的问题,改进了搜索思路,可以有效搜索各非支配解的邻域,并简化每次搜索的流程,增加了算法迭代次数。 本文设计了多组实验来测试IMOGA的性能。所有实验在Intel(R)Core(TM)i7-8550U CPU@1.80 GHz双核处理器16.00 G的计算机上完成,NSGA-Ⅱ采用软件MATLAB 2019A编写。实验中,各机器的工人标准安装时间si和机器标准加工时间pi分别满足[1,15],[5,25]的均匀分布;两两机器之间工人的行走时长tlj由坐标值满足[1,10]的均匀分布的点计算得到,M=5,10,15,20,ni在区间[1,20]和[5,25]随机取值,因此实验共有4×2=8种场景,每种实验场景生成10个案例;a=-0.322。本文采用不同算法求解所有实验案例,从以下方面对实验结果进行分析比较。为统一标准,所有算法生成解数量为100的解集,并设定相同的时间阈值TotalTime。 本文引入Hypervolume指标衡量多目标算法的求解效果。Hypervolume指标是衡量求解多目标优化算法较为公正的指标[30-31],可以衡量解集的综合性能。Hypervolume指标评价方法由Zitzler等[32]提出,表示解集中的个体与参考点在目标空间中所围成的超立方体的体积,用式(15)计算,Hypervolume指标值用H表示。实验选择坐标(1.2,1.2)作为参考点,将两目标值分别归一化后进行计算,H值越大,解集的收敛性越好。 (15) 为对比不同解集对算法的影响,本文构造了7种方法生成初始解集,解集规模为100,分别是: (1)r=0,0.01,…,0.99,分别用MOGL各生成1个解。 (2)r=0,1,分别用MOGL各生成50个解,即生成多个两目标的极端解。 (3)r=0,1,分别用MOGL各生成1个解,其余98个解以随机方式生成。 (4)r=0,0.25,0.5,0.75,1,分别用MOGL各生成20个解。 (5)r=1,用MOGL生成100个解,即解集中全部为以最小化最大完工时间为目标的极端解。。 (6)r=0,用MOGL生成100个解,即解集中全部为以最小化行走时间为目标的极端解。 (7)随机生成100个解。 表1所示为不同初始解集时IMOGA的Hypervolume指标值,算法的参数取值为w=10,G=200,TotalTime=0.5N。观察不同方式的均值可得,方法2的效果最好。方法2的特点是对每个目标执行贪婪算法的次数最多,因此可以得到尽量优质的极端解,其对解集的扩展起积极的作用,这一点通过与方法1和方法4对比得到。方法1和方法4增加了初始解的均匀性和广泛性,通过图2可见方法1生成的初始解集的分布。但是方法1和方法4计算两目标极端解的次数少,不能得到较优的极端解,在算法执行时间较长时,初期广泛性的优势不再明显,而方法2生成的解集中极端解的优势可以更好地体现出来。方法3与方法1、方法4的差别不大,但其解集中极端解的数量已经减少到最小,说明了极端解在初始解集中的重要性,对于本文问题,初始解集中只要包括两个极端解,便可得到相对较优的结果。对比方法5和方法6可知,如果解集中只有一个目标的极端解,则以最小化行走时间为目标的极端解构成的初始解集优于以最小化最大完工时间为目标的情况,更接近包括两个极端解的初始解集的结果。方法7是将随机解集作为初始解,其效果远不如其他方法,因此采用本文提出的MOGL计算初始解集可以有效提升算法性能。下文均以方式2作为初始种群的生成方式。 表1 不同初始解集时IMOGA的Hypervolume指标值 为更明显地体现不同解集对算法的影响,图2展示了方法1生成的初始解集和以方法5~方法7生成初始解集的IMOGA对某一案例的求解结果,执行时间(单位:s)分别为N,0.5N,0.25N,0.125N,案例的M=10,ni在区间[1,20]随机取值。方法2~方法4生成初始解集的IMOGA的结果与方法6近似。观察图2a可见,在算法执行时间较短时,方法1生成初始解集的IMOGA的结果优于随机解集的结果;方法5生成最小化最大完工时间解的优势明显,但是最小化行走时间解的效果不佳,因此其非支配解集的收敛程度和广泛性不如方法6;方法6生成的初始解集使IMOGA能够在较短时间内得到较广泛的非支配解集,其各方面性能明显优于方法5和方法7。观察图2b~图2d可见解集的变化趋势,随着算法执行时间的增长,方法7生成初始解集的IMOGA的结果逐渐向方法5靠近,方法6生成初始解集的IMOGA的结果逐渐向最小化最大完工时间的方向收敛。 综合分析得,初始解集中两个极端解越优质,IMOGA的效果越好;相对最小化最大完工时间为目标的极端解,以最小化行走时间为目标的极端解可以使IMOGA获得更好的结果;随机初始解集和全部以最小化最大完工时间为目标的初始解集时IMOGA的效果明显不如其他初始解集。 本文以w=10,G=200,TotalTime=0.5N为基准参数,分别变化w,G,TotalTime,统计结果如表2所示。当问题规模较小时,w对IMOGA的影响不稳定,随着问题规模的增加,当w=20时,算法的求解效果较好。当问题规模较小时,G取值较大时的算法效果较好,随着问题规模的增加,较小的G可以获得更优解,原因是G的取值影响算法中贪婪邻域搜索的频率,频率越大,算法的效果越好。显然,TotalTime越大算法的优化效果越好,但是随着执行时间的增长,优化效果的变化幅度减小,说明算法逐渐收敛于Pareto前沿。 表2 不同参数时IMOGA求解结果的Hypervolume指标值 为证明IMOGA的有效性,本文将其与传统的NSGA-Ⅱ和IPG两种启发式算法进行了对比,结果如表3所示。其中传统的NSGA-Ⅱ改变了每代交叉得到的新染色体的数量,分别为NP,2NP,4NP;IMOGA的参数为w=10,G=100,TotalTime=0.5N;初始解集通过4.1节的方法1生成;传统IPG采用文献[26]的算法。可见,IMOGA在各种规模时均能得到较优的解集,相对传统的IPG,其Hypervolume指标值可以提高15.07%,证明了本文对传统IPG改进的有效性,其原因是简化的邻域搜索保证了算法的迭代次数,增加了搜索效率。因为传统的NSGA-Ⅱ以随机方式生成初始解集,限制了其优化效果,改变传统NSGA-Ⅱ染色体交叉的数量虽然对结果有一定影响,但是作用不明显,所以采用IMOGA所得结果的Hypervolume指标值比传统NSGA-Ⅱ平均提高31.78%。总之,传统型NSGA-Ⅱ解决本文问题的能力随问题规模的增加逐渐下降,而IMOGA、传统IPG和MOGL解决问题的能力比较稳定。因此在规模较大时,传统型NSGA-Ⅱ所得解集的Hypervolume指标值不如MOGL,MOGL所得解集的平均Hypervolume指标值水平略低于传统IPG。 表3 IMOGA与传统算法的Hypervolume指标值对比 为去除初始解集对不同算法的影响,本文对比了基于同样初始解的传统NSGA-Ⅱ和IMOGA的求解效果,如表4所示。IMOGA在不同求解时间和不同问题规模下的求解效果均略高于传统NSGA-Ⅱ,其Hypervolume指标值平均提高2%。另外,问题规模越大、执行时间越长,IMOGA的优势越明显,这与贪婪邻域搜索的执行次数有关,适当频率的贪婪邻域搜索可使算法得到更优的结果。因此,贪婪邻域搜索对优化算法有效。 表4 不同时间阈值时IMOGA与传统型NSGA-Ⅱ的对比 综上所述,本文所提IMOGA的优越性主要体现如下: (1)针对问题中的学习效应提出MOGL,得到较优的极端解,因此IMOGA有较好的搜索起点,算法可以搜索的邻域更加广阔。 (2)变异增加了算法的随机搜索能力,在计算前期可以迅速扩展解空间,后期辅助解集跳出局部最优。 (3)基于贪婪的邻域搜索对每个非支配解都进行有针对性和方向性的邻域搜索,其搜索效率更高,推动了解集向Pareto前沿收敛。 (4)采用NSGA-Ⅱ作为基本框架,使算法可以保留随机搜索和定向搜索获得的精英解,有效地保证了解集的广泛性和均匀性。 本文针对单人单工序多机作业车间的最小化最大完工时间和工人行走时间多目标调度问题建立数学模型,其融合了基于贪婪的邻域搜索方法和NSGA-Ⅱ,提出并应用MOGL构建初始解集,设计了IMOGA。设计实验表明IMOGA可以有效求解该问题,因此本文研究可以有效解决单人管理多台设备、需要同时考虑工人行走时间和加工时长的作业车间调度问题,所引入的学习效应模型提高了解决问题的准确性,决策者可以根据实际情况选择解集中的调度方案,具有较高的灵活性,然而构建学习效应模型或确定学习因子需要对工人的操作行为进行大量实验。 由于IMOGA中基于贪婪的邻域搜索执行时间受问题规模的影响较大,会降低解决更大规模问题时的效果,下一步研究将着手改善该问题。另外,单人作业车间导致各机器不能及时作业,造成资源和能源浪费,因此补充最小化资源和能源消耗也是未来研究的方向。4 仿真实验
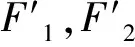
4.1 初始解对IMOGA的影响

4.2 参数对IMOGA的影响
4.3 IMOGA与传统算法的对比
5 结束语

