地铁车辆轴箱吊耳断裂机理分析及优化

杨 雨 周劲松 孙 煜 尤泰文 宫 岛

(同济大学铁道与城市轨道交通研究院， 201804， 上海∥第一作者， 硕士研究生)

轴箱吊耳作为转向架的安全部件，在车辆整体起吊时起到悬挂与限位保护作用[1]。目前,对于吊耳在设计寿命内断裂问题已引起国内学者关注，文献[2-3]对吊耳断裂的问题采用拓扑优化方法，将吊耳固有频率避开激励中振幅较大处。文献[4]将有限元分析和线路试验相结合，开展轴箱吊耳断裂机理研究，提出对钢轨打磨以降低吊耳的振动加速度幅值。但采用钢轨打磨的方式成本较高，且地铁运营一段时间，钢轨磨耗后又需再次打磨。

一般而言，轴箱吊耳设计寿命30年(或360万km)[5]，但某型地铁车辆在投入运营后不足1年，其轴箱吊耳就发生异常断裂，断裂位置多集中在吊耳根部螺栓孔上方，如图1所示。为解决此问题，本文首先通过试验，分析轴箱吊耳振动加速度谱；然后建立轴箱吊耳有限元模型，进行模态和疲劳[6]分析，确定断裂原因；最后通过优化，改善轴箱吊耳振动模态，提高其疲劳寿命。

图1 轴箱吊耳断裂实物照片

1 轴箱吊耳试验

为考察轴箱吊耳在车辆运行过程中所受动载荷及振动性能，对该地铁车辆在实际线路下轴箱吊耳横向冲击加速度以及动应力进行了测试。轴箱吊耳试验测点布置如图2所示。由于该车辆轴箱吊耳断裂主要发生在其根部与轴箱连接处，因此在轴箱吊耳根部两侧对称布置应变传感器，采集应力幅值；轴箱吊耳顶部布置加速度传感器，采集振动信号；同时在车体下方靠近轴箱吊耳处安装监控摄像头，以监视其与构架的接触与碰撞情况。

图2 轴箱吊耳测点布置规划图

通过对试验采集到的数据从时域角度进行分析，得到轴箱吊耳在车辆实际线路运行过程中测点部位的横向振动加速度和应力分布情况，主要关注信号的幅值和均方值的大小。在该时间历程中，轴箱吊耳结构受到的应力最大值为142.36 MPa。信号的均方值表达了信号在此段时间内的强度，其均方根值(RMS)称为有效值，也是信号平均能量的一种表达。

根据测试结果，RMS值为91.74 MPa。载荷信号的幅值和均方根值均未超过轴箱吊耳结构材料的许用应力值172.5 MPa，说明故障并非由于材料强度不足所致。

同时由实时监控记录显示，轴箱吊耳结构没有与构架发生碰撞的现象，运行过程中也没有受到其他物体的撞击，说明其断裂不是由冲击载荷所致。

将轴箱吊耳两测点时域信号经过傅立叶变换，得到测点加速度频谱图。它反映了信号的频率成分及其分布，如图3所示。频谱分析表明，轴箱吊耳振动的主频在330 Hz附近，此频段内的振幅较大，且在某频率段峰值很高，振动能量主要集中在320～350 Hz的频段内，其他频段的能量占比较小。

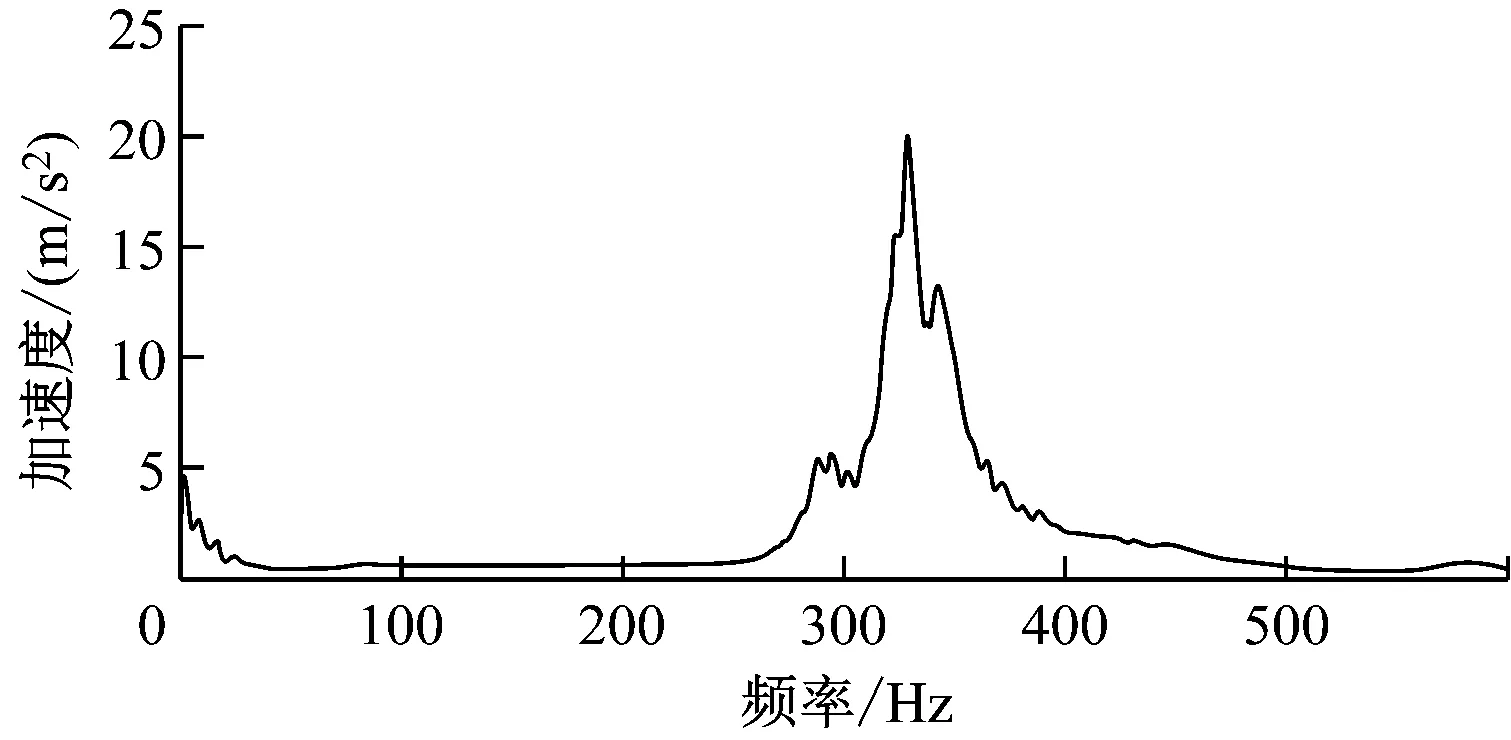
图3 轴箱吊耳加速度频谱分析图

为分析轴箱-吊耳的振动传递情况，采用传函分析方法，以轴箱振动信号作为输入，轴箱吊耳振动信号作为输出，分析轴箱到轴箱吊耳的振动传递。如图4所示，轴箱到轴箱吊耳的振动传递，在343.11 Hz附近振动幅值最大，即轴箱与轴箱吊耳之间的传递幅值最大，与其振动主频集中在320～350 Hz范围的频谱分析相吻合，说明轴箱吊耳结构在此频段内发生了共振[7]。

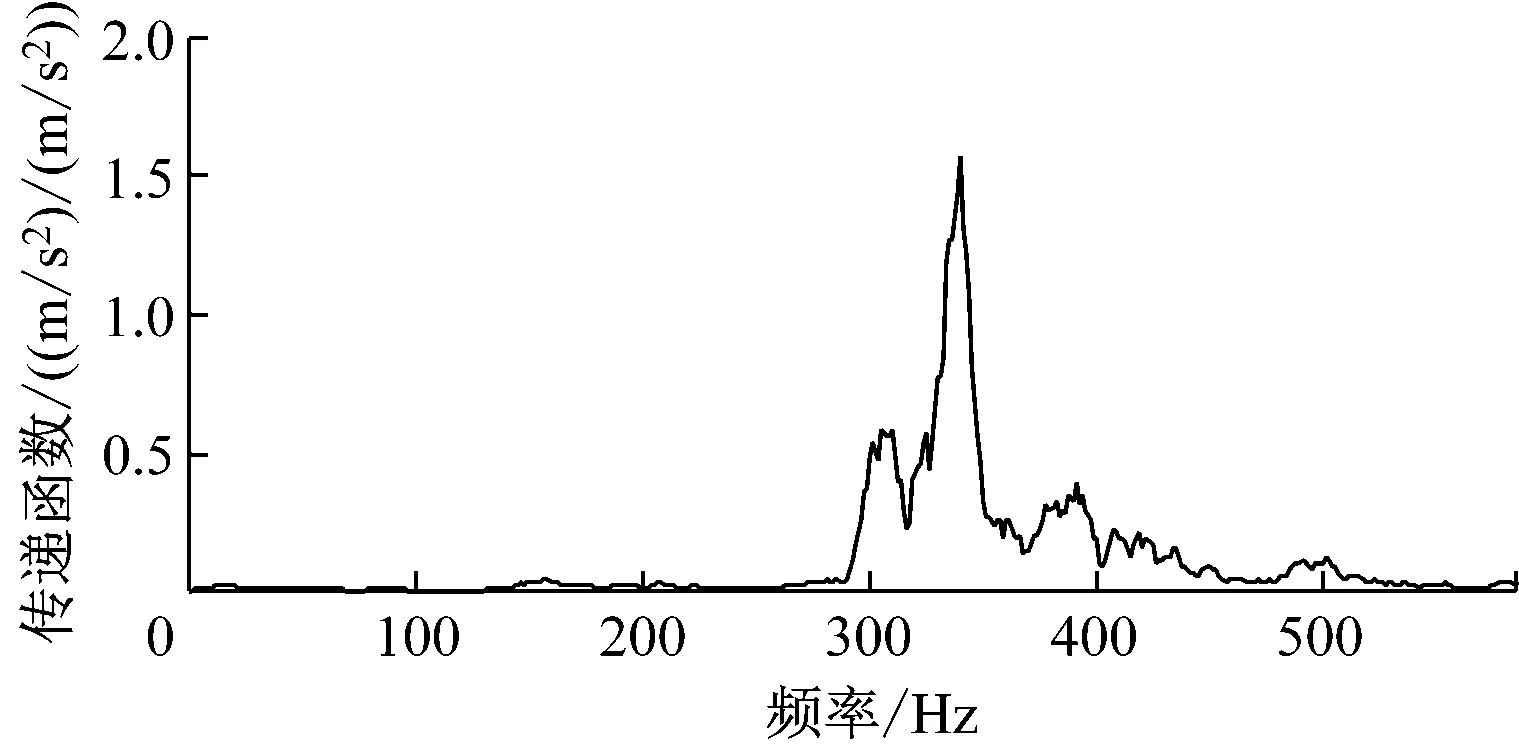
图4 轴箱-吊耳传函幅值变化规律

2 轴箱吊耳模态分析

通过以上分析可知，轴箱吊耳在轴箱的振动作用下发生共振，导致其受到高水平应力的交变载荷，造成结构因疲劳失效而断裂。为进一步验证轴箱吊耳断裂原因，本节建立轴箱-吊耳有限元模型，对轴箱-吊耳进行模态分析和疲劳分析。

建立轴箱-吊耳三维实体模型，导入有限元软件Hypermesh中，将轴箱-吊耳离散为大小2 mm、总数为479 726的Solid187四面体单元，两者之间采用Bolt螺栓连接。单元网格jacobin值0.7，网格划分合理。轴箱-吊耳三维模型与有限元模型如图5和图6所示，轴箱-吊耳结构的前四阶弹性模态振型如图7所示。

图5 轴箱-吊耳三维模型图

图6 轴箱-吊耳有限元模型图

a) 337.52 Hz(横向弯曲)

b) 552.54 Hz(纵向弯曲)

c) 964.23 Hz(扭转弯曲)

d) 1 321.79 Hz(纵向弯曲)

由轴箱-吊耳前四阶弹性模态应力分布图可知，轴箱-吊耳结构应力薄弱区域在吊耳中部、吊耳与轴箱端盖连接处和轴箱端盖连接板等位置。前四阶弹性模态的固有频率计算结果如表1所示。第一阶弹性模态的频率为337.52 Hz，与传递率峰值出现的频率相对应，说明轴箱吊耳的振动过大是由于轴箱激起吊耳一阶横向弯曲模态，导致共振。

表1 轴箱-吊耳结构模态计算结果

3 轴箱吊耳疲劳分析

在4个端盖螺栓孔处施加全约束和试验中得到的轴箱加速度功率谱载荷[8-10]，按照Dirlik方法[8]对轴箱吊耳进行随机振动疲劳分析。Dirlik通过蒙特卡洛技术进行时域仿真，将宽带平稳随机振动的幅值概率密度近似为一个指数分布和两个瑞利分布，并由此得到Dirlik疲劳损伤模型为：

式中：

C、b——材料参数;

D——与功率密度有关的函数;

Γ——Gamma函数;

R——与功率密度有关的函数;

Q——随机载荷的分布概率函数;

v——随机载荷的分布自由度;

D1、D2、D3——模型推导过程中产生的与材料性质和随机分布概率有关的参数。

当应力载荷为宽带随机过程时，单位时间应力的循环次数等于单位时间应力峰值的个数，即峰值穿越率。

通过时域仿真，输出危险点在随机激励下的应力谱如图8所示。图8中按照雨流计数法统计了响应点的应力谱，输出点处的应力呈非正态分布，应力主要集中85～254 MPa，最大循环次数为50 000次左右。

图8 雨流计数法处理寿命最小处应力谱

轴箱吊耳疲劳寿命云图如图9所示。计算的结果表明，运行工况下轴箱吊耳疲劳寿命最小值为144 544次，出现在其下段靠近轴箱处；轴箱吊耳与轴箱端盖连接柄处寿命也较小，寿命较小的节点主要集中在连接板上。因为轴箱吊耳是通过连接板与轴箱接触的，轴箱将载荷传递给轴箱吊耳，作为轴箱与轴箱吊耳的连接部件，连接板分担了纵向大部分外载，局部应力比较大，其他部位的寿命大多趋于无限寿命。断裂部位主要在轴箱与轴箱吊耳连接处，损伤最大部位可承受的最小循环次数为144 544次，相应的加速度谱对应时间为300 s，则总的持续时间为12 045 h。

该激励下车辆行驶速度为50 km/h，可计算出轴箱吊耳的最大行驶里程约为60万km。因此，轴箱吊耳不满足车辆厂提出的360万km行驶寿命。这与实际运行时轴箱吊耳断裂发生的时间50万km接近，存在误差的原因可能是在对轴箱吊耳进行疲劳分析时，未考虑轴箱吊耳表面的机械加工特性等对材料强度的影响[11]。

4 轴箱吊耳结构优化

根据以上分析可知，轴箱吊耳断裂是由于其结构固有频率与激励频率接近而导致共振，最终使其断裂，实质为模态匹配不合理。为解决该问题，需将轴箱吊耳结构固有频率与激励频率相隔离。改变轴箱吊耳固有频率的一般方案为调整吊耳厚度和宽度，或进行形貌优化。

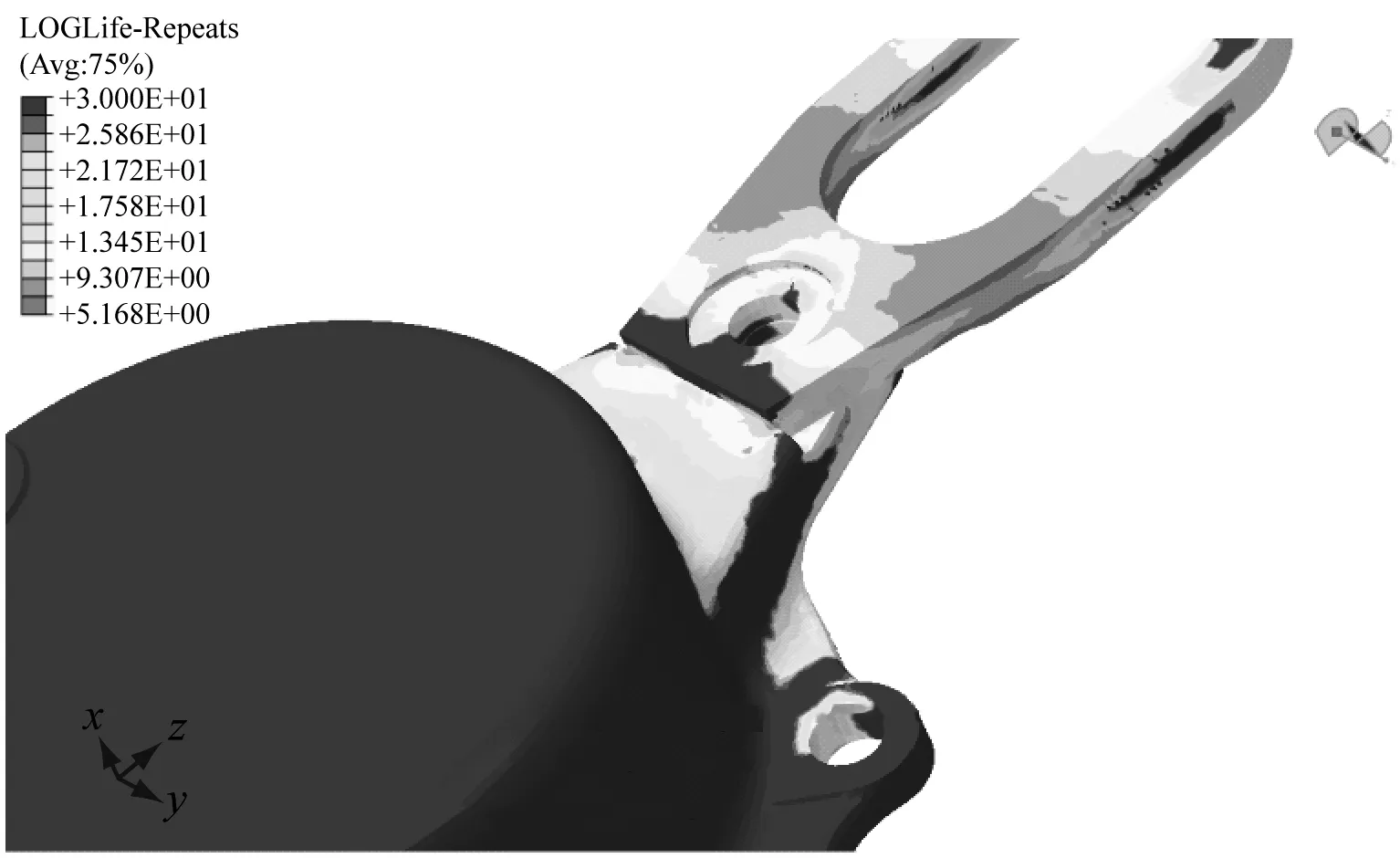
图9 轴箱吊耳疲劳寿命云图

轴箱吊耳螺栓孔及内部限位环的大小和位置由于装配需要，为固定的定形或定位尺寸。优化思路是将吊耳根部易断裂处增宽，材料不变，提高其低阶(横向)模态频率进行模态匹配[12]，使优化后结构的一阶固有频率避开振动主频(330 Hz)。同时，由于轴箱端盖的配合部位对于轴箱吊耳根部强度没有明显影响，出于节约材料的考虑[13]，将端盖配合处改为窄方形。优化前后的轴箱吊耳结构对比如图10所示。

a) 优化前

b) 优化后

优化后的轴箱吊耳结构一阶模态结果如图11所示，对应频率为552.54 Hz，与激励主频330 Hz相差较大，这样可保证不会由于频率区段重合而发生共振。

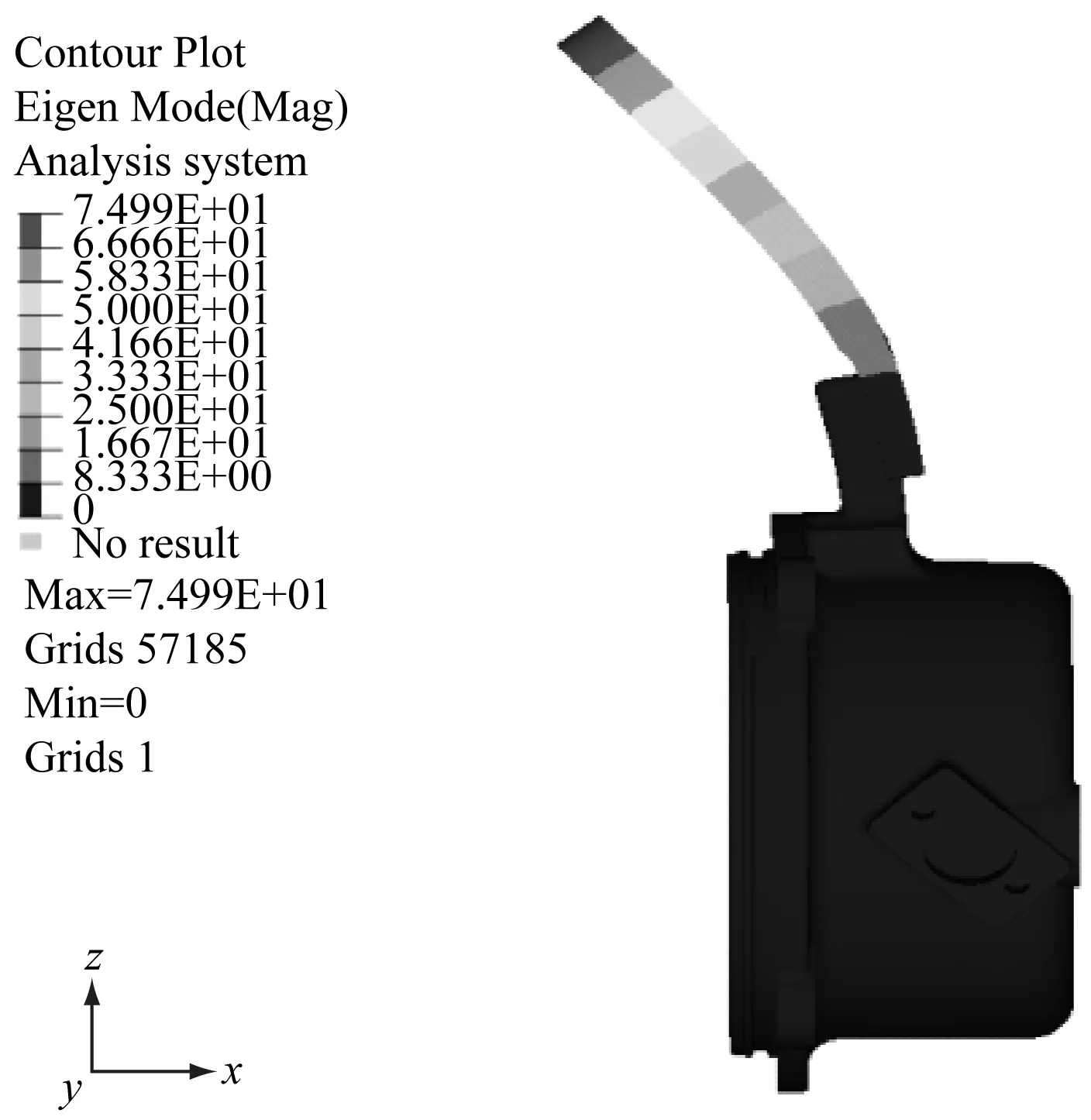
图11 轴箱吊耳优化后一阶模态结果

优化后的轴箱吊耳疲劳寿命云图如图12所示。计算结果表明，运行工况下轴箱吊耳的疲劳寿命最小值为1 096 478次，易产生劳损的位置为端盖连接柄根部及轴箱吊耳根部。加速度谱对应时间为300 s，且认为实际运行时条件不变，则总的持续时间为91 373 h，可计算出吊耳的最大行驶里程为456万km，符合车辆厂提出的使用要求。

5 结语

本文针对某型城轨车辆轴箱吊耳异常断裂问题，根据线路测试结果进行频谱分析与传函分析，发现轴箱吊耳振动主频与传递率峰值相重合。通过结构模态和疲劳寿命仿真计算，发现车辆在实际运行的工况下，第一阶弹性模态被激起，使轴箱吊耳振动过大，导致疲劳断裂。最后对轴箱吊耳结构进行了形貌优化，将轴箱吊耳固有频率与轴箱振动主频相隔离，避免共振的发生。通过仿真计算验证，优化结果满足轴箱吊耳的疲劳强度要求。

a) 吊耳整体疲劳云图

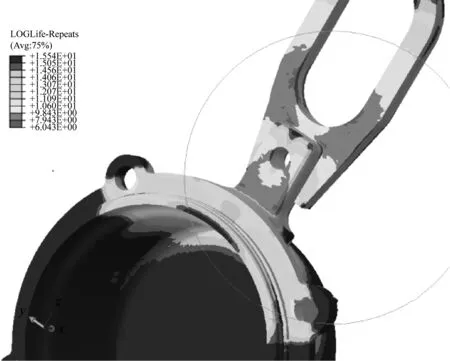
b) 优化部位疲劳云图