城市轨道交通信号系统对曲线段速度要求的计算*
黄克勇
(南京铁道职业技术学院通号学院, 210031, 南京∥正高级工程师)
在城市轨道交通中,列车行驶在曲线线路上时会产生离心力,使乘客产生不舒适感,并且有侧翻的危险。为了平衡离心力,在轨道上采用设置曲线超高来平衡离心力。曲线超高设置与速度等多个参数相关,设置不好可能造成列车侧翻。通常设置的曲线超高如不足或过大,会出现欠超高或过超高的现象,虽然增加的超高会平衡一部分离心加速度,但未被平衡的离心力仍然存在[1]。针对未被平衡的离心加速度值,各国的要求和标准都不一样,但判定的原则都是按乘客无不良反应的值作为依据。我国城市轨道交通信号系统的标准中规定,在曲线处的离心加速度,即横向加速度应不大于0.4 m/s2,信号系统根据这个要求和其他相关专业给出的数据来计算在曲线处的最高速度是否合适[2]。
在城市轨道交通的工程设计中,每个专业(如行车、土建、车辆和信号等专业)对正线路段的最高速度都有不同的要求。由于信号系统是保证列车运行安全、实现行车指挥和提高运输效率的关键系统设备,所以最终的最高限速需要信号专业进行控制和计算。其中,曲线路段的速度关系到整个轨道交通系统运营的安全,其计算涉及多个专业且计算过程相对复杂,因此对曲线段速度的计算是否合适,信号专业在完成招标后的工程设计阶段应根据各个专业提供的具体数据进行详细的计算和最终的确认[3]。
1 曲线段最大速度的计算模型
1.1 信号专业与其他专业对列车运行速度的协调
信号专业对曲线段的列车速度计算通过以下方法和其他专业进行协调:在城市轨道交通的工程设计中,行车专业按列车每站停车原则进行牵引计算,得出全线曲线地段的理论运行速度;然后行车专业的牵引计算速度作为轨道专业的计算依据,确定曲线地段线路超高值;而线路专业是依据技术标准中确定的列车在曲线地段上运行的最高速度设置缓和曲线的长度。由于这些设计和计算出来的曲线段最高速度是在初步设计阶段已经完成,此时信号系统还没有开始招标。
在信号系统招标前,信号专业需根据行车专业提供的资料,结合国内地铁车辆的特性参数、各信号系统供货商提供的列车控制系统的控制水平,提出信号系统正常控制模式,即ATO(列车自动运行)模式或ATP(列车自动防护)模式下的列车运行触发紧急制动的速度值,以及触发紧急制动后综合考虑各种最不利条件下的列车瞬间最高运行速度值,作为配合土建专业设计的基础资料。
在信号系统招标后,信号专业根据其自身系统控制原理进行系统性能分析时,系统控制列车在曲线地段的实际运行速度(包括最高ATO推荐速度、紧急制动触发速度及可能达到的最高速度)。本文给出的紧急制动触发速度和可能达到的最高速度,与线路、轨道专业设计依据的速度值会有所不同,因而信号专业须重新计算列车在曲线地段线路上运行时,触发紧急制动后可能达到最高速度时的横向加速度值不应大于0.4 m/s2,其冲击率(Jerk)不应大于0.3 m/s3。如果超过,则必须由轨道专业调整超高值,或由信号专业降低推荐的最高速度、紧急制动触发速度及可能达到的最高速度[4]。
1.2 计算模型
列车在曲线段的运动受到离心力的影响会产生横向的加速度,受加速度变化率影响的横向冲击率也会发生变化,冲击率过大会严重影响到乘客乘坐的舒适性。为了确定曲线段的最大速度是否合适,采用安全制动模型,研究和计算在运营速度下列车在曲线段产生紧急制动的触发速度vEBIC和可能达到的最高速度vmax,以保证曲线地段最高限制速度大于或等于信号ATP系统触发紧急制动后列车可能达到的最高速度[5]。考虑到城市轨道交通信号系统中列车可以在同一线路上正、反方向双向运行,信号系统也提供列车双方向运行的ATP功能,因而对同一线路上正、反方向运行的列车都要进行计算。在对正方向运行的列车进行计算后,列车的横向加速度如果超过0.4 m/s2,冲击率超过0.3 m/s3,此时要降低信号系统的推荐最高速度及紧急制动触发速度,使列车在可能达到最高速度时的横向加速度不超过0.4 m/s2,横向冲击率不超过0.3 m/s3。
对于曲线路段最高速度采用“安全制动模型”来计算,因为通过“安全制动模型”计算出来的紧急制动触发速度和可能最高速度可以反映出列车在曲线路段的最不利情况。列车在曲线路段的运行速度,需要满足小于列车紧急制动触发速度。
如图1所示,列车在触发紧急制动后分成最大牵引阶段(时间Tt)、惰行阶段(时间Te)和制动阶段,最大牵引阶段的时长又分为牵引系统响应时间(Tt1)和牵引切除时间(Tt2)。在最大牵引阶段,列车会受到牵引力上升到最大,随后由于制动还没有响应,进入惰行阶段,惰行阶段结束后车辆才真正施加紧急制动。
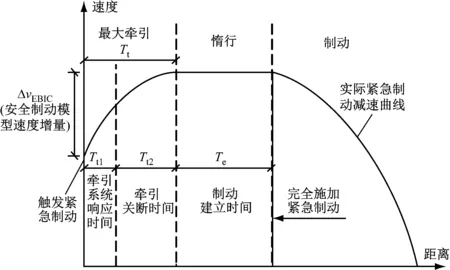
图1 安全制动模型
根据紧急制动减速曲线速度、安全制动模型产生的速度增量和速度裕量,计算得到紧急制动触发速度(vEBIC)。安全制动模型描述了紧急制动触发时,从车载ATP发出紧急制动指令直至紧急制动施加时最不利情况下的速度变化。具体根据车辆牵引系统响应时间Tt1、切除列车牵引所需时间Tt2、从牵引切除到制动系统建立保证制动率的紧急制动所需的时间Te、当前速度下的最大牵引加速度at和坡度造成的附加加速度apmin,计算其产生的速度增量ΔvEBIC[6]。
ΔvEBIC计算公式如下:
ΔvEBIC=(at+|apmin|)Tt+|apmin|Te
(1)
式中:
at——当前速度下的最大牵引加速度;
Tt——牵引系统响应和牵引切除延时;
|apmin|——根据当前坡度计算的重力分量对列车的附加加速度。
坡度上的重力附加加速度如图2所示。

注:g为重力加速度。
根据坡度计算的重力附加加速度公式:
|apmin|=|gd|
(2)
式中:
d——当前最大坡度。
在计算紧急制动触发速度时还需考虑速度裕量,该值与列车测速的误差有关。
2 曲线段的计算
2.1 曲线段计算
根据允许的横向加速度和横向冲击率,可得到曲线处的速度限制。根据我国地铁设计标准,横向加速度为0.4 m/s2,冲击率为0.3 m/s3。根据vEBIC和vmax分别计算横向加速度以及冲击率为:
vmax=vG+vpr+vtc
j=(avmax)/ltransit
式中:
vmax——最坏情况下,可以达到的最大速度,m/s;
vG——运营速度,m/s;
vpr——速度余量,m/s;
vtc——紧急制动命令后牵引和惰行阶段中的速度增长量,m/s;
c——曲线处的超高,m;
r——取决于vmax的曲线半径,m;
a——曲线引发的横向加速度,m/s2;
j——取决于vmax的横向冲击率,m/s3。
ltransit——缓和曲线长度。
列车质量mtotal:AW0(空载)为151.506 t,AW1(满座)为163.986 t,AW2(额定载荷)为222.726 t,AW3(超载)为252.666 t。
列车阻力Fw的计算公式为:
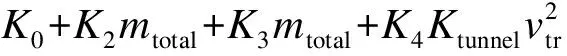
式中:
K0——阻力的经验参数,取3.096×10-3N;
K2——质量的经验参数,取6.374×10-3N/kg;
K3——质量的经验参数,取0.329 1×10-3/s;
K4——速度的经验参数,取11.187 kg/m;
Ktunnel——隧道的类型,取2个;
vtr——列车速度。
如果在隧道外,列车阻力公式Ktunnel取值为1。vEBIC包括速度控制裕量和速度误差,前者是预先设定的固定值,verr基于现有驾驶速度v0线性增加,且符合:
If (v0<30 km/h), thenverr=2 km/h
elsev0=2 km/h+(v0-30 km/h)/47
由Fw可得到v0下曲线段允许的最大加速度,如表1所示。

表1 根据Fw计算得到的不同v0下的曲线段最大允许加速度
2.2 曲线速度表
按照上述的计算方法,以实际线路苏州地铁2号线正线部分某区段计算出来的曲线速度表进行示例,根据其他专业提供的圆曲线半径、缓和曲线长度、超高、坡度和vG,计算出vEBIC和vmax;然后分别计算出这两个速度下的a和j,检查计算出的a是否小于0.4 m/s2和j是否小于0.3 m/s3。表2和表3的计算结果都满足这个结果,且符合国家标准的要求。如果a超过0.4 m/s2,j超过0.3 m/s3,则需要线路专业调整线路参数或者信号专业降低曲线段的运营速度[8]。
对于不设缓和曲线的特殊曲线横向j不用计算。
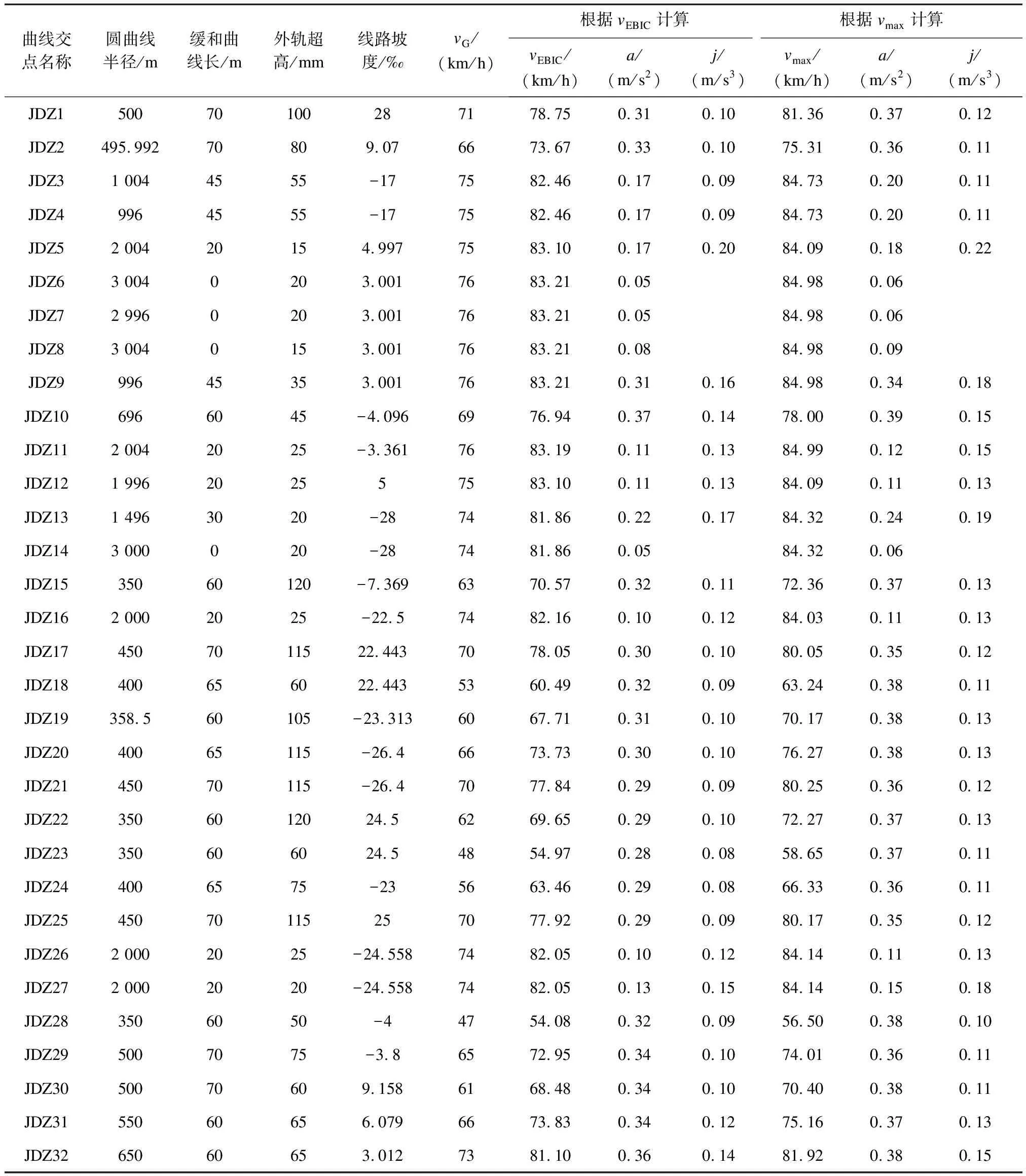
表2 苏州地铁2号线某区段左线的曲线段a和j
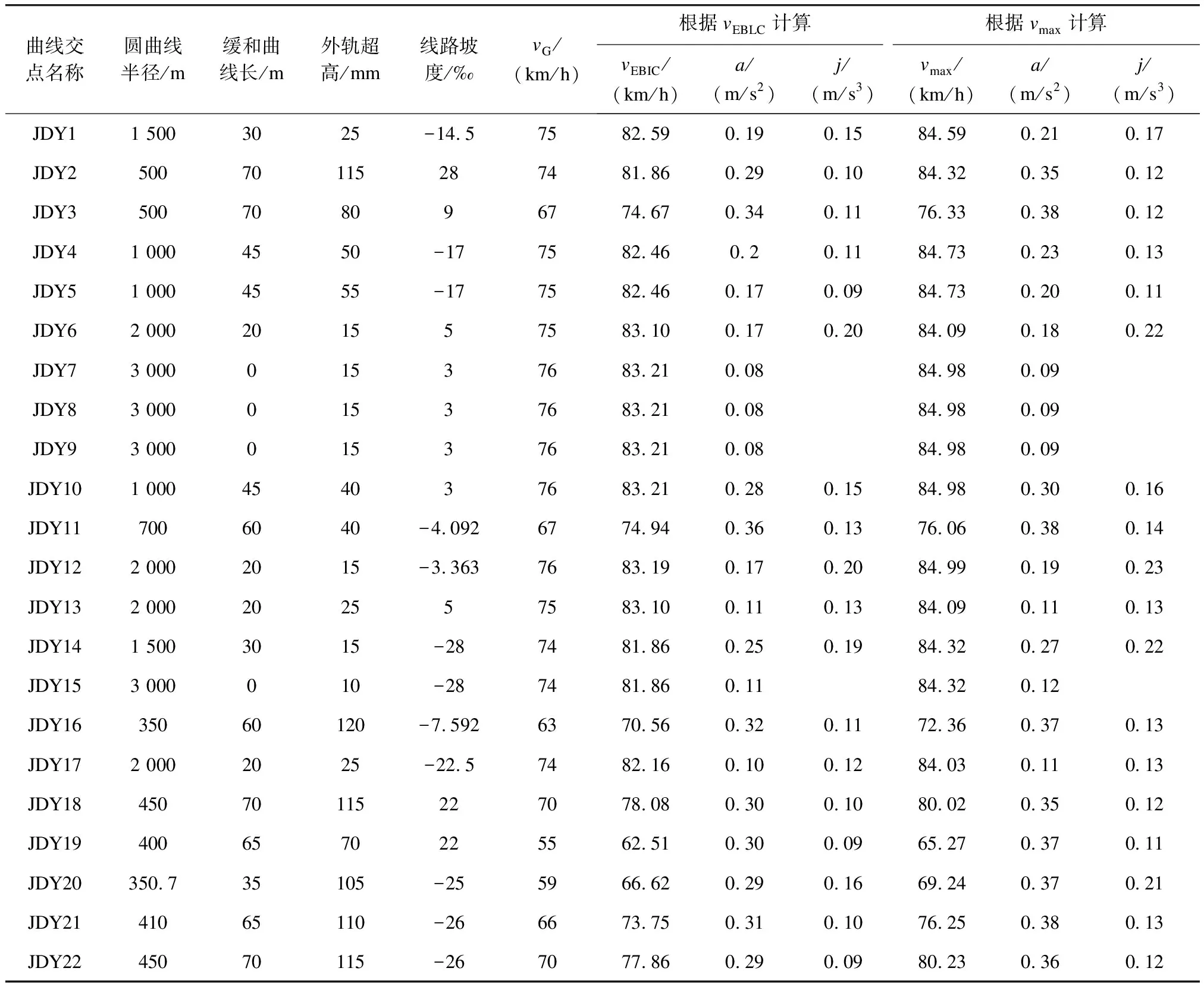
表3 苏州地铁2号线某区段右线的曲线段a和j
3 结语
本文从城市轨道交通信号专业角度,对曲线段最高速度的计算方法以及调整方法进行了研究和介绍。主要方法是以安全制动模型为计算依据,根据线路、轨道和车辆等其他专业提供的数据,计算出曲线段运营速度下的紧急制动触发速度和可能的最高速度,并分别计算这两种速度下的横向加速度和冲击率是否满足乘客舒适性的要求和相应的国家标准要求。

