高精度双斜坡辅助式混沌布里渊光纤动态应变传感*

王亚辉 赵乐 胡鑫鑫 郭阳 张建忠乔丽君 王涛 高少华 张明江†

1) (太原理工大学, 新型传感器与智能控制教育部与山西省重点实验室, 太原 030024)

2) (太原理工大学物理与光电工程学院, 太原 030024)

近年来, 基于受激布里渊散射的分布式光纤传感技术已广泛应用于土木结构健康监测、灾害预警、国防安全等诸多领域, 振动等动态参量的实时传感和精准检测已成为备受瞩目的研究热点.本文提出一种基于增益开关调制和双斜坡辅助的混沌布里渊光相关域分析传感技术, 实现高精度、大范围动态应变监测.首先, 理论分析了单斜坡辅助系统中混沌激光固有的时延特征和功率随机波动特性对测量精度的影响和限制; 然后,利用增益开关调制产生48.6 dB的高消光比脉冲, 使得混沌信号时延旁瓣和非零基底诱发的噪声场被大幅抑制, 仿真结果表明声波场信噪比提升3.31 dB, 实验测得混沌布里渊增益谱信号背景噪声比提升1倍, 动态应变测量精度由 ± 40.2 µe提高至 ± 23.1 µe; 最后, 利用双斜坡辅助技术, 消除混沌激光固有功率波动的影响,动态应变测量精度进一步提升至 ± 8.1 µe, 系统稳定性良好, 且动态范围仍保持800 µe, 为现代传感网络的高精度、大范围动态应变监测提供了一种新的解决方案.

1 引 言

21世纪以来, 大型工程安全监测需求日趋严峻, 分布式光纤传感技术在智能电网、油气管网、交通基础设施、水利工程、军事边境安防等重要领域已获得广泛应用[1,2].其中, 基于受激布里渊散射(stimulated Brillouin scattering, SBS)的光时域分析技术(Brillouin optical time-domain analysis,BOTDA)[3]和光相关域分析技术(Brillouin optical correlation-domain analysis, BOCDA)[4]由于其监测距离长、空间分辨率高、可实现温度应变多参量监测等优势而深受关注.然而, 传统的SBS传感器需通过耗时的频率扫描过程使得探测光与泵浦光的频率失谐量匹配光纤布里渊频移(Brillouin frequency shift, BFS)以激发有效的SBS作用, 测得布里渊增益谱(Brillouin gain spectrum, BGS)并依其中心频率解调光纤沿线任意位置的温度、应变信息.因此, 传统SBS传感器的动态实时性受到严峻挑战, 多用于静态监测, 而不适于动态应变等参量的测量[1−4].

为满足现代传感网络对动态变化参量实时监测的重大需求, 国内外研究者们针对动态应变测量范围与监测实时性从两个方向提出了多项创新解决方案[5,6].1)快速重构振动位置的BGS, 并依据其中心频率实现动态应变解调.例如, 美国Voskoboinik等[7]提出将探测光频率调制为光频梳的免扫频BOTDA技术可以30 kHz的速率解调BGS,以色列Peled等[8]利用任意波形发生器将探测光频率切换速率提升至8 kHz, 哈尔滨工业大学董永康团队[9]利用光学啁啾链式BOTDA系统将测量速率提升至6.25 MHz; 然而, 上述系统均属于基于脉冲光源的BOTDA技术, 动态应变监测频率与光纤长度成反比, 且空间分辨率受限于脉冲宽度而难以突破1 m.因此, 日本Hotate团队[10]与上海交通大学何祖源团队[11]分别利用压控振荡器构建了快速扫频BOCDA系统, 该方案可实现振动频率与光纤长度无关的高速单点测量, 空间分辨率达厘米量级; 但与上述BGS快速解调方案类似, 系统成本与复杂度明显提升, 动态应变测量范围与振动频率无法兼顾, 实用性严重受限.2)无需重构BGS的斜坡辅助技术(slope assisted, SA), 该技术将探测光频率锁定在BGS上升沿或下降沿线性区并实时监测该频率下动态应变引起的探测光功率变化, 根据BGS线性范围内增益与频移的一一对应关系实时解调动态应变[12], 斜坡辅助方案由于其成本低、技术简便、适应性强而备受青睐.例如,Peled等[13]首次提出单斜坡辅助(single-slope assisted, SSA)BOTDA技术实现了400 Hz动态应变检测, 但由于BGS谱宽较窄(30 MHz), 应变范围被限制在400 µe; 为提升应变测量范围, 布里渊增益-相移比[14]、BGS谱型调控[15]、多斜坡辅助[16−18]等技术先后被应用于BOTDA系统, 动态范围提升至5000 µe, 然而系统复杂度持续上升且空间分辨率仍受限.因此, 何祖源团队[19]提出双斜坡辅助(dual-slope assisted, DSA)BOCDA技术将系统空间分辨率突破至厘米量级, 但受限于BGS谱宽其动态应变范围仅150 µe.

最近, 本课题组提出一种大范围动态应变监测的单斜坡辅助混沌BOCDA技术(SSA chaotic BOCDA, SSA-CBOCDA), 混沌激光独特的宽带光谱特性将混沌BGS本征展宽, 线性范围扩展至55 MHz; 基于此, SSA-CBOCDA系统不仅将空间分辨率提升至3.45 cm, 而且将动态应变范围拓展至1200 µe[20,21].然而, 混沌激光自相关旁瓣和基底在光纤沿线引入一系列SBS噪声场, 导致系统信噪比较差, 且混沌激光固有的功率波动使得动态应变-功率响应存在大幅无规则振荡, 这两项因素导致SSA-CBOCDA系统动态应变测量误差明显高于其他SA系统.

为实现高精度动态应变监测, 本文提出一种基于增益开关调制和双斜坡辅助的混沌布里渊光相关域分析动态应变传感技术.首先, 本文利用增益开关将SSA-CBOCDA泵浦路进行高消光比的脉冲强度调制, 仿真结果验证待测光纤(fiber under test, FUT)中残留的SBS噪声场被大幅抑制, 实验结果显示BGS的信号背景噪声比(signal-to-background ratio, SBR)被明显提升, SSA技术动态应变测量精度由 ± 40.2 µe提高至 ± 23.1 µe; 为继续消除混沌激光固有功率波动的影响, 本文提出DSA-CBOCDA方案, 实验验证DSA技术可实现0.7 dB功率波动无关的动态应变解调, 最终利用该方案将动态应变测量精度提升至 ± 8.1 µe, 且测量范围仍保持800 µe.

2 实验装置

斜坡辅助式混沌布里渊光相关域分析动态应变传感技术实验装置如图1所示, 混沌激光由单反馈环结构产生并经90/10的光耦合器分为两路, 其中上支路(90%)作为探测光, 下支路(10%)作为泵浦光.探测光经边带调制器(sideband modulator, SBM)进行载波抑制的双边带调制, 边带频移量约等于光纤BFS, 且SBM由微波信号源(KEYSIGHT, N5173 B, 9 kHz—13 GHz)和电光调制器(electro-optical modulator, EOM, EOSPACE, 12.5 Gb/s)组成.调制后的混沌激光依次经可编程光延迟发生器(programmable optical delay generator, PODG, General Photonics, ODG-101)

实现传感点的定位、掺铒光纤放大器(erbiumdoped fiber amplifier, EDFA1, Connet, MFAS-CB-LP)将探测光功率放大至7 dBm、扰偏器(polarization scrambler, PS, General Photonics, PCD-104)降低布里渊增益的偏振敏感效应, 最终通过光隔离器(isolator, ISO)注入到FUT末端.泵浦光经强度调制器将连续混沌激光调制为脉冲混沌激光, 然后经过EDFA2(Keopsys, CEFA-C-PB-HP)和光环行器(optical circulator, OC)注入到FUT前端, 其中EDFA2将泵浦光峰值功率放大至33 dBm.两路光在FUT中发生SBS作用, 被放大的探测光通过OC输入到带宽6 GHz的带通滤波器(band pass filter, BPF, Yenista, XTM-50), 滤出的斯托克斯光被光电探测器(photodetector, PD, Finisar,XPDV2120R)接收、锁相放大器采样(lock-in amplifier, LIA, AMETEK, Model 7270 DSP), 最终由计算机处理与分析.FUT由30 m的普通单模光纤(G.652)构成, 其中光纤末端10 cm放置于电动位移拉伸平台(华维浩润, ASC-N)上以施加动态拉伸应变.需要指出, 本实验采用的混沌激光带宽与课题组在文献[21]中的工作类似, 即混沌激光自相关曲线的中心峰宽度约0.36 ns, 系统空间分辨率约3.6 cm.

图1 斜坡辅助式混沌布里渊光相关域分析动态应变传感技术实验装置图.插图A为相同输出功率下混沌激光器与分布式反馈半导体激光器的输出信号时序, 插图B为混沌激光自相关曲线和多阶相关峰示意图, 插图C为连续混沌激光被调制为脉冲混沌激光Fig.1.Experimental setup of SA-CBOCDA for dynamic strain sensing.Inset A, the time series of chaotic laser and that of DFB-LD under the same output power.Inset B, the autocorrelation curve of chaotic laser and the schematic diagram of multiple order correlation peaks.Inset C, the continuous chaotic laser being amplitude-modulated into pulse chaos.

如图1插图A所示, 混沌激光输出时序呈现大幅度、无规则的振荡, 本文所使用混沌激光输出功率为500 µW, 其时序振荡峰峰值可达7.8 mV,是相同输出功率下分布式反馈半导体激光器

(distributed feedback laser diode, DFB-LD)输出时序峰峰值的6.5倍, 且两者的均值都保持在28 mV.斜坡辅助技术中, 动态应变的大小决定了固定频率下探测光的实时布里渊增益.根据BOCDA技术传感原理, 探测光强度的增益过程可用如下公式表示[22]:

其中,Is和Ia分别为被SBS增益前后的探测光强度,Ip为泵浦光强度,gB为光纤布里渊增益系数,∆z表示光纤中相关峰的宽度(即理论空间分辨率).由(1)式可知, 探测光强度的变化主要决定于单位空间分辨率距离内泵浦光提供的SBS增益GSBS=gBIp∆z.在CBOCDA系统中, 由于混沌激光的时域振荡特性, 泵浦光强度可表示为Ip(t)=Ip0·u(t) , 其中Ip0为均值强度,u(t) 为强度随时间的振荡函数(定义为泵浦光强度波动因子), 因此布里渊增益及探测光强度均随时间大幅度振荡; 同理可知, 传统基于DFB-LD的传感系统中, 泵浦光强度可近似表示为Ip=Ip0, 故由泵浦光强度波动引起的增益波动极其微弱.

此外, 探测光增益还会受到光纤中相关峰的影响.在理想的CBOCDA系统中, 由于混沌激光时序自相关曲线的类δ函数特性, 任意距离FUT中存在唯一的0阶相关峰z0, 仅在该峰内激发有效的SBS效应.然而, 混沌激光固有的时延特征(time delay signature, TDS)导致其自相关曲线中心峰两侧存在一系列旁瓣峰, 且自相关基底也呈现随机起伏的振荡状态; 上述旁瓣峰zn,n=±1,2,···和非零基底zbase会在FUT中激发一系列的SBS声波场.如图1插图B所示, 假设以此混沌激光为探测信号, 当FUT长度为120 m时, 除中心位置外,FUT中还存在至少8阶旁瓣峰, 即同时激发产生了至少16个强度明显的噪声SBS声波场; 此外,非零基底zbase也会激发随光纤长度不断累积的微弱噪声场.因此, 中心峰位置处的GSBS被进一步干扰恶化, 最终测得的探测光强度可表示为

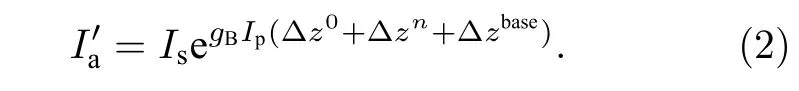
为了抑制系统背景噪声, 本课题组已经提出时域门控方案[23], 如图1插图C所示, 连续混沌激光被调制为脉冲混沌激光, 脉冲持续时间τp与单反馈混沌环腔长对应时间一致.此时, 混沌泵浦光强度修正为

其中 r ect(ξ) 为矩形脉冲函数, 仅当时取值为1.因此, 脉冲混沌泵浦光理论上可使光纤中仅存在z0,zn,n=±1,2,···和zbase则被完全抑制; 实际上, 脉冲调制消光比将直接影响噪声场的抑制程度, 由于混沌激光的振荡特性, 本文定义消光比(extinction ratio, ER)为脉冲高电平时间内信号强度均值与脉冲基底时间内信号强度均值之比;当ER值较大时以τp时间内z0激发的SBS效应为主, 当ER值较小时随光纤长度逐步累积(T−τp时间内)的zn,n=±1,2,···和zbase噪声增益占据主导.

综上所述, SA-CBOCDA系统中泵浦光为探测光提供的SBS增益可表示为

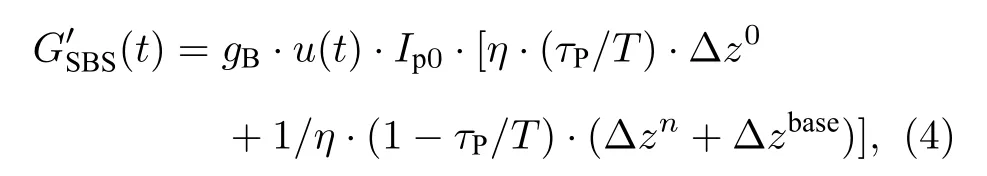
其中,τp和T分别表示最佳的脉冲持续时间和脉冲信号周期;η表示泵浦脉冲调制ER值, 且η1 ,η=1表示未施加脉冲调制.由(4)式可知, SACBOCDA系统中,同时受泵浦光强度波动因子u(t) 和脉冲调制消光比η的影响, 探测光强度存在较大的固有波动和噪声干扰; 由于探测光功率(确定的光纤系统中, 探测光强度变化可等价于探测光功率变化)与动态应变的线性对应关系, 导致动态应变测量精度明显弱于基于DFB激光的SA系统.为抑制系统噪声增益源, 本文提出基于增益开关的高消光比脉冲调制和基于双斜坡辅助的免泵浦功率波动依赖技术, 最终实现高精度的动态应变测量.

3 实验结果与分析

3.1 基于增益开关调制的动态应变精度提升

原始时域门控CBOCDA系统中, 连续混沌泵浦光被EOM调制为脉冲光, 通过调节射频脉冲电压控制信号消光比; 然而, EOM自身特性只能提供小于40 dB的消光比, 且存在插入损耗大、消光比不稳定、偏压控制复杂等缺点[24], 导致传统时域门控系统的脉冲消光比差、系统复杂度高、背景噪声抑制不完全.因此, 提出基于增益开关(gain switch, GS)的调制方案, 实现高且稳定的消光比而进一步提升信噪比(signal-to-noise ratio, SNR)、降低系统复杂度.

图2 不同调制方式及作用效果 (a)不同调制方式下脉冲混沌光时序及消光比; (b)不同调制方式下仿真的混沌受激布里渊声波场强度及信噪比Fig.2.Different modulation methods and the corresponding effects: (a) The time series of pulse chaos and ERs of these under different modulation modes; (b) simulation results of chaotic SBS acoustic field amplitude and the corresponding SNR.

图2 (a)所示为实验测得原始状态、EOM调制与GS调制混沌激光时序, 并对不同调制方式下的消光比ER=20·log(Vpeak/Vbase) 进行了对比分析.由图2(a)可以看出, EOM调制提供仅25.1 dB的ER值, GS调制消光比可达48.6 dB, 比EOM调制提升了约23.5 dB.根据(4)式可知, GS的高消光比调制可大幅抑制zn,n=±1,2,···和zbase噪声峰, 为了验证这一效果, 本文首先仿真模拟了不同调制情况下的SBS声波场强度.如图2(b)所示, 黑色曲线为连续混沌激光入射30 m光纤中时的声波场分布情况, 已知混沌激光时延腔长为5 m, 因此除光纤中心15 m处z0外, 10与20 m处存在强度较大的z±1, 5与25 m处甚至存在z±2; 此外, 混沌激光自相关基底激发的SBS噪声强度也被清晰观测到.混沌SBS声波场信噪比定义为中心峰强度Acp与噪声峰峰值强度Anp的比值SNR=10·log(Acp/Anp), 则基于连续混沌激光的SBS声波场SNR约为5.69 dB.EOM调制系统中,z±1和zbase被抑制效果明显,z±2几乎完全消失, SNR值也提高至8.33 dB, 然而未完全消除的噪声峰仍会随光纤长度持续累积并恶化探测光的SBS增益.GS的高消光比调制使得z±1,2和zbase几乎均被完全抑制, SNR提升至11.64 dB, 约为基于连续混沌激光系统的2倍, 且与EOM调制系统相比也有3.31 dB的提升.

根据本课题组的早期研究结果[23,25,26], CBOCDA系统噪声峰的抑制效果将直接体现为混沌BGS的SBR值水平, 因此, 本实验继续对比了不同调制方式下的混沌BGS.为了更好地比较分析BGS包络及SBR, 将EOM调制和GS调制系统中测得的混沌BGS进行了归一化处理, 如图3所示.可以看出, GS调制系统背景噪声水平明显更低, 其SBR值为15.22 dB, 约为EOM调制系统的2倍.此外, 图3插图为测得的原始增益谱, 可以看出, GS高消光比调制显著提升了SBS增益强度, 通过PD探测到约0.013 mV的峰值增益增量.GS调制实现了与长腔反馈混沌激光[21]相同的噪声抑制效果, 且实用性更强、易于实现长距离高信噪比BGS测量.此外, 已知SA技术是通过探测锁定频率下的布里渊增益实现动态应变解调的, 因此, 优化后的增益谱可促进理论上获得更精确的动态应变测量.

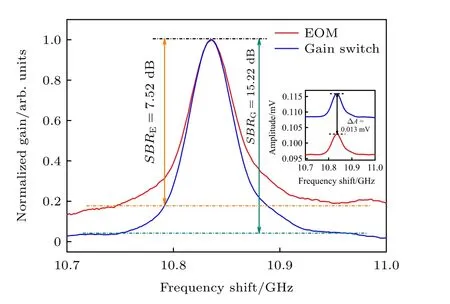
图3 不同调制方式下的归一化混沌布里渊增益谱及其信号背景噪声比; 插图为测得的原始布里渊增益谱Fig.3.Normalized chaotic BGSs and SBR analysis of these,under different modulation modes.Inset view: the measured original BGSs, corresponding to the main view.

基于图1所示的实验装置, 泵浦路分别利用EOM和GS实现脉冲强度调制, 探测光频率锁定在混沌BGS下降沿10.865 GHz处, 通过电动拉伸位移平台的往复运动提供动态应变.为保证探测光功率对动态应变的线性响应, 本实验施加的动态应变大小为0—800 µe, 消除由功率-应变转换系数引起的测量误差[20].图4(a)和图4(b)分别给出了EOM调制与GS调制下SSA-CBOCDA系统测得的动态应变时序及其正弦拟合曲线, 由图可知, 两种调制方式下动态应变值均可被准确地解调.为了表示测量精度, 本文首先比较了两条正弦拟合曲线的相关系数R2, GS调制系统的相关系数0.9793略大于EOM调制系统, 但均接近于1, 表明两者的拟合结果均较好, 但是GS调制系统的相关性更高.此外, 本文详细分析了两种调制方式下的动态应变测量误差, 如图4(c)所示, 蓝色和红色点图分别表示EOM调制、GS调制系统中15次独立重复测量的动态应变误差均值及不确定度, 插图为单次测量误差的测算依据和典型结果.EOM调制系统中误差明显更大, 标准偏差σE为 ± 40.2 µe, 相对误差达 ± 5.0%.经过GS调制改进, SSA-CBOCDA系统动态应变测量误差σG降低至 ± 23.1 µe, 相对误差缩小为 ± 2.9%.此外, 不同调制系统中标准偏差的不确定度均较小, 进一步表明精度测量结果准确性高、系统稳定性好.图4(d)所示为两种调制方式下测得的动态应变的振动频率, 结果表明基频1.3 Hz和二次谐振频率2.6 Hz均可被准确检测; 需要指出, 本实验采用的电动位移拉伸平台由一对步进电机控制, 电机的低速往复运动导致振动频率较低, 下一步将考虑使用压电陶瓷振荡器提供高频的动态应变.

综上所述, 在基于增益开关调制的SSA-CBOCDA系统中, 混沌激光旁瓣峰和非零基底引起的SBS增益噪声被大幅抑制, 动态应变测量精度提升了约1.7倍.然而, 由(4)式可知, GS调制并不能消除由混沌激光固有功率波动u(t) 导致的测量误差; 此外, GS调制会导致脉冲高电平持续时间内更强的功率波动, 因此本文提出双斜坡辅助技术继续提升动态应变测量精度.

图4 不同调制方式下的动态应变测量结果 (a) EOM调制系统动态应变测量时序及正弦拟合曲线; (b) GS调制系统动态应变测量时序及正弦拟合曲线; (c)两种调制方式下的动态应变测量误差, 插图为单次测量典型结果; (d)两种调制方式下的动态应变频率Fig.4.The results of dynamic strain measurement under different modulation modes: (a) Time series and sine fitting curve of dynamic strain in EOM modulation system; (b) time series and sine fitting curve of dynamic strain in GS modulation system;(c) measurement error of dynamic strain under two modulation modes, inset view is the typical result of a single measurement;(d) vibration frequency under two modulation modes.

3.2 基于双斜坡辅助的动态应变精度提升

斜坡辅助技术中, 上升沿锁定频率v+下的对数型探测光增益可表示为[19]

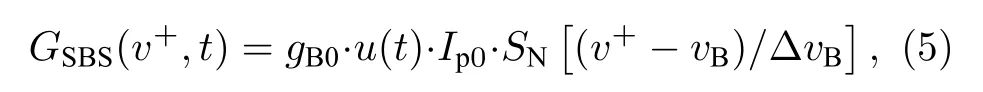
其中,gB0表示有效布里渊增益系数且仅与光纤材料、光路偏振状态有关(在确定的系统中可认为是常 数),vB表示应 变、温 度 等引起的BFS, ∆vB为BGS线宽(本实验中混沌BGS线宽约50 MHz),SN(vB)为归一化的BGS.

同理可得, 下降沿锁定频率v−下的对数型探测光增益可表示为

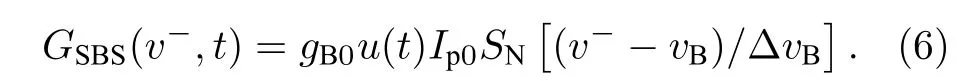
由(5)式和(6)式可以发现, 无论频率锁定在上升沿或下降沿, 探测光增益均与泵浦光强度(即泵浦光功率)成正比, 因此可得两个确定频率下的增益比RB为

经过双斜坡比值分析可知, 动态应变大小仅与锁定频率下的增益大小有关, 与泵浦光功率无关.

图5详细分析了DSA方法的原理, 以归一化的混沌BGS(蓝色虚线)为例, 分别取上升沿与下降沿中心频率v+,v−为锁定频率, 此时两点频率间隔恰好为BGS线宽v−−v+=∆vB, 保证最大化利用混沌BGS的本征宽谱特性; ∆v表示动态应变引起的相对BFS, 易知 ∆v=0 时RB=0 , 保持间隔 ∆vB并以v+,v−为中心在BGS谱线上取不同大小应变引起的 ∆v对应的增益值, 最终求得如图5红色实线所示的RB分布曲线.由图可知,RB曲线至少拥有40 MHz的线性区间(紫色圆点所示, –20—+20 MHz), 即可精确测量的动态应变范围至少为800 µe.

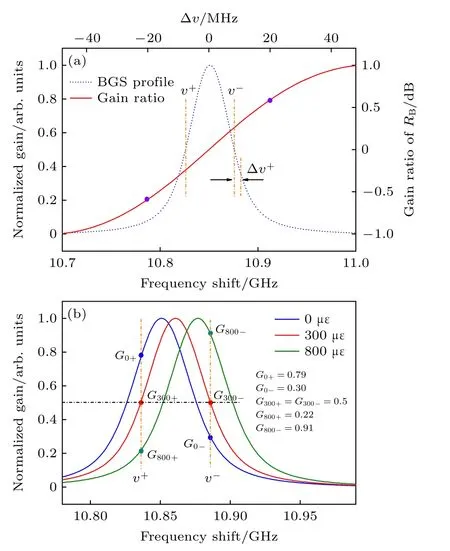
图5 双斜坡辅助技术原理示意图 (a)布里渊增益比的理论分析; (b)布里渊增益比实验标定的理论模型Fig.5.Principle of DSA method: (a) theoretical analysis of RB ; (b) theoretical model for experimentally calibrating R B.

如前所述, 为了免除光纤松弛对测量结果的影响, 本实验将光纤拉伸段施加约300 µe的预拉伸, 并基于此状态下的增益谱选定频率v+,v−.如图5(b)所示, 此时G300−≈G300+≈0.5 , 即RB≈0 dB; 当施加应变分别为0和800 µe时, 根据图中圆点标识, 计算得增益比值分别约为–0.42和0.62 dB, 均保持在图5(a)RB曲线所示的线性区内.具体实验时, 如图6(a)所示, 分别测量两个频率下施加不同大小准静态应变时的探测光时序, 计算得不同应变对应的RB曲线; 由图6(a)可以看出,0与800 µe时RB取值与理论分析基本一致, 当应变以200 µe步进从0 µe增加至800 µe时,RB几乎呈现线性上升趋势, 且300 µe时RB值近似于0 dB.不同应变对应RB的均值被进一步提取并做线性拟合, 如图6(b)所示, 相关系数RR2约等于0.9990表明了RB与应变值的良好线性关系; 根据曲线斜率可得, 该DSA系统的最终增益比—应变转换系数Cs约为0.0012 dB/µe.

为了验证DSA技术可以消除泵浦功率波动影响, 本文测量了基于上升沿和下降沿中心频率锁定的SSA动态应变响应时序, 动态应变大小为0—600 µe, 同时手动添加了泵浦光先减后增的大范围功率波动.如图7(a)所示, 无论上升沿或下降沿频率锁定, SSA技术均可实时反映动态应变引起的布里渊增益强度变化, 然而其响应时序呈现与泵浦光功率一致的先下降后上升趋势, 峰值功率波动达0.7 dB, 无法利用功率-应变转换系数准确解调动态应变大小.根据DSA技术原理, 将图7(a)中的两列时序进行比值计算并利用Cs解调便得图7(b)中蓝色曲线所示动态应变序列.可以看出,动态应变大小已被准确还原, 利用正弦拟合曲线进一步验证了较好的动态应变测量正确度(相关系数R2≈0.9642).

图6 双斜坡辅助系统的增益比-应变转换系数 (a)不同大小准静态应变对应的增益比曲线; (b)根据线性拟合曲线计算的转换系数Fig.6.Estimate of the conversion coefficient, C s , between the strain value and R B in DSA system: (a) TheRB curves under different quasi-static strain; (b) final coefficient calculated from the linear fitted curve.

基于上述验证实验和转换系数, 本文在仅有混沌激光自身功率波动的情况下, 利用DSA技术进行了动态应变大小及精度的最终测定.如图8所示, 图8(a)中蓝色曲线为实际测量的动态应变时序, 0—800 µe动态应变被准确测量; 对测量值做如红色点图所示的正弦拟合, 拟合相关性高达0.9972; 同时如图8(b)中蓝色点图所示, 通过15次独立重复测量计算得应变测量误差σD为 ± 8.1 µe,插图即为单次测量误差的测算依据和典型结果; 相对误差下降至 ± 1%, 动态应变测量精度明显提升.动态应变标准偏差的不确定度仅± 1.0 µe, 表明了双斜坡辅助系统具有更好的测量准确度和系统稳定性.此外, 动态应变振动基频1.3 Hz也被准确检测, 动态应变频率与SSA系统测量结果一致(电动位移平台的运动速度并未改变).

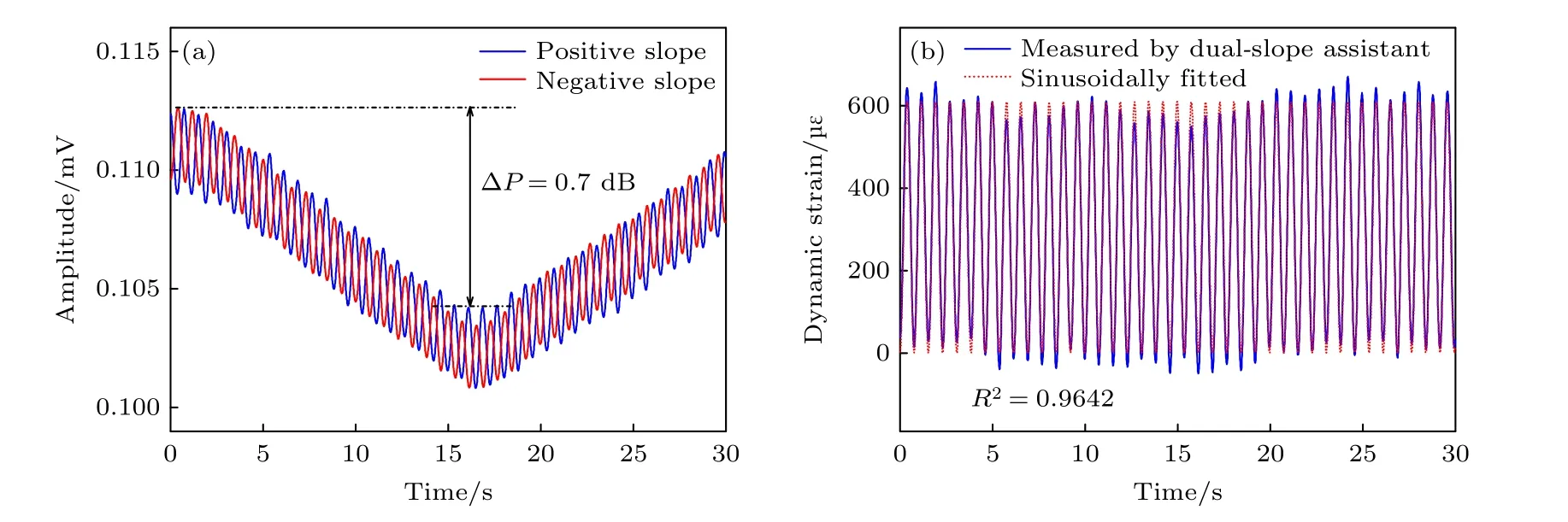
图7 双斜坡辅助技术消除泵浦功率波动影响的验证实验 (a)手动施加泵浦光功率波动时利用单斜坡辅助技术测得的动态应变响应时序; (b)双斜坡辅助技术解调的动态应变大小Fig.7.The verification experiment of pump-power-independent measurement by using DSA method: (a) Measured Brillouin amplitude using SSA method when a dynamic strain is applied with a manual change of pump power; (b) measured dynamic strain using DSA method.

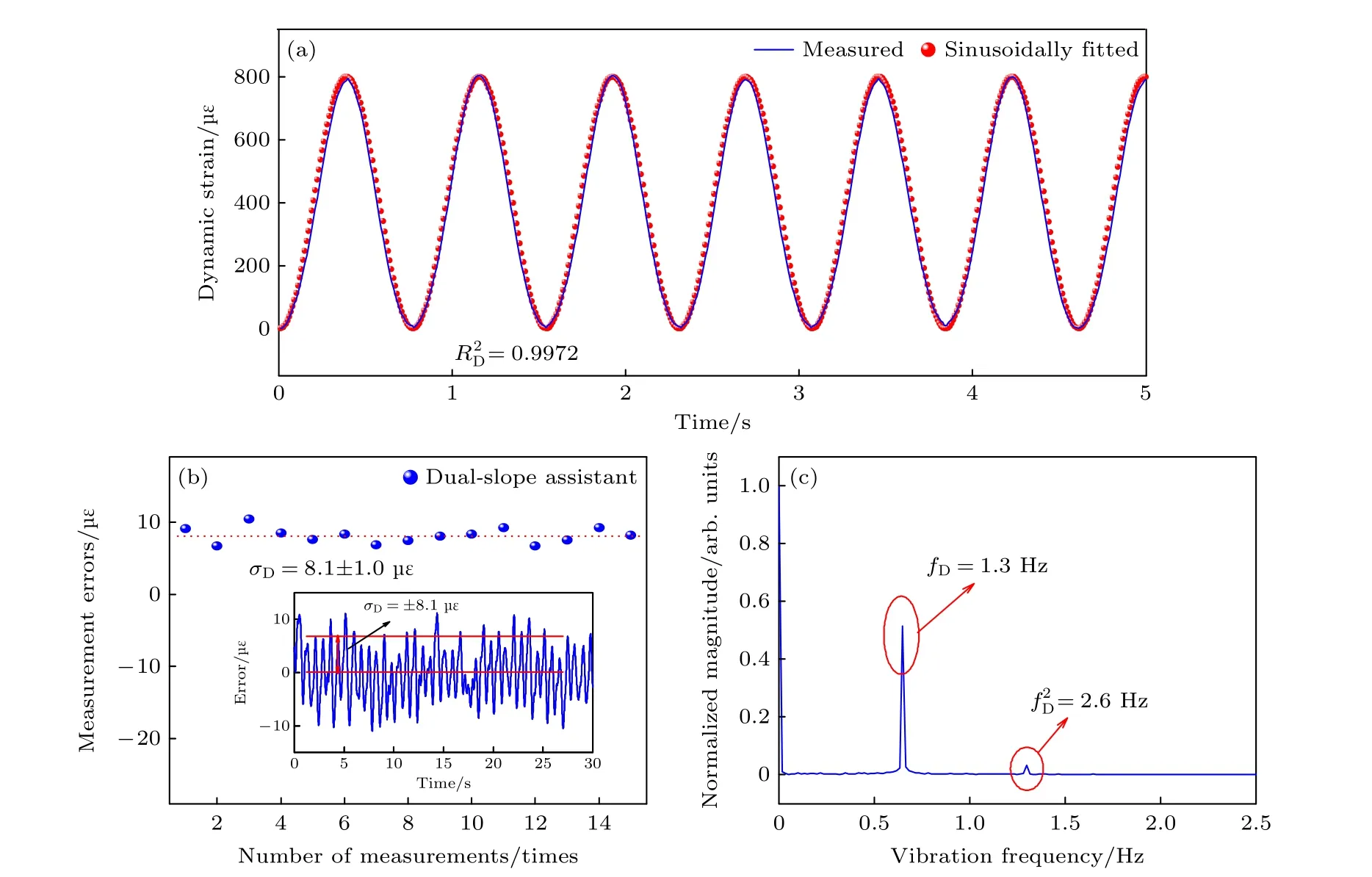
图8 施加0−800 µe时的双斜坡辅助系统动态应变测量结果 (a)动态应变测量时序及正弦拟合曲线; (b)动态应变测量误差,插图为单次测量典型结果; (c)动态应变振动频率Fig.8.Measurement results of DSA system when a dynamic strain of 0−800 µe is applied: (a) Measured time trace and sine-fitted curve; (b) measurement error, inset view is the typical result of a single measurement; (c) vibration frequency.

4 结 论

本文提出了一种高精度的斜坡辅助式混沌布里渊光相关域分析动态应变传感技术.首先, 理论分析了混沌激光固有的功率随机波动特性、自相关曲线旁瓣峰和随机基底对SA-CBOCDA系统测量精度的影响和限制; 其次, 利用增益开关实现48.6 dB的高消光比脉冲调制, 与EOM调制系统相比, 仿真得GS调制可将SBS声波场的信噪比提升3.31 dB、实验测得GS调制可将混沌BGS的信号背景噪声比提升1倍, 实验证明动态应变测量精度由 ± 40.2 µe提高至 ± 23.1 µe, 相对误差从± 5.0%缩小为 ± 2.9%, 且标准偏差不确定度由± 3.3 µe降低至 ± 2.5 µe; 最后, 实验验证了双斜坡辅助技术可免除大范围泵浦功率波动的影响,DSA-CBOCDA系统将动态应变测量精度再次提升至 ± 8.1 µe, 相对误差仅 ± 1%, 动态范围仍保持0—800 µe, 且标准偏差不确定度仅 ± 1.0 µe,实现了高精度、大范围、高稳定的动态应变传感.与SSA-CBOCDA系统相比[20,21], 本文方案的动态应变测量精度提升显著, 约为原来的5倍, 测量范围略微下降为原来的 2 /3 , 下一步将继续开发多斜坡辅助技术拓展动态范围.与现有的DSA系统相比[16,19], DSA-CBOCDA系统测量精度基本一致,但是测量范围远大于150 µe.此外, 本文动态应变振动频率受步进电机低速运动和LIA低采样率的限制而保持在Hz量级, 未来研究中将采用压电陶瓷振荡器提供高频的动态应变和高速数字示波器进行实时采样, 将振动频率提升至kHz量级.综上所述, 本文实现了一种高精度、大范围动态应变监测的DSA-CBOCDA系统, 同时保持厘米级高空间分辨率, 将为现代工业中动态变化参量的精准定位和实时监测提供一种新型解决方案.