直管中黏弹性流体二次流的非线性特性分析*

花少震,段翠芳,刘华博,孟凡净,王强胜,孔春辉

(河南工学院 机械工程学院,河南 新乡 453003)

0 引言

二次流是流体流动过程中叠加于主流动上的次生流动,是自然界中流体流动时广泛存在的一种自然现象,例如飓风、马桶抽水时的漩涡、弯曲河道处的水流漩涡、高分子的爬杆现象、塑料共挤成型的界面不稳现象[1]等。除了离心力、科式力、流体的弹性可以诱发二次流外,二次流的产生还与流体流动区域的形状有关。除了黏弹性流体,其他流体在直管中流动均不会有二次流产生。

对黏弹性流体二次流现象机理的探究始于20世纪50年代,目前依然缺乏深入研究。对于黏弹性流体,一般认为二次流的产生是由于第二法向应力差N2引起的,但当第二法向应力差系数和剪切黏度成正比时,不会出现二次流现象[2]。较多的研究集中在探索第二法向应力差和第二法向应力差系数同二次流的关系上[3-5]。此外,SYRJL[6]用Reiner-Rivlin和Criminale-Ericksen-Filbey(CEF)模型模拟出了与流动方向截然相反的涡,并以此建立了在该黏弹性本构方程下的二次流流动准则,但这种准则不适用于其他的积分型和微分型黏弹性本构方程,如PTT,Lenonv,Giesekus等模型。Yue[7]用Giesekus模型,采用有限元方法以及求解析解的方法,发现当第二法向应力差对剪切速率的一阶导数同剪切黏度对剪切速率的一阶导数的比值为正时,二次流从拐角处流向中心,反之相反。黏弹性流体是一种广泛存在的流体,研究黏弹性流体的二次流产生机理可以为分析黏弹性流体的流动提供理论依据,例如塑料加工、石油输送、血液流动等。

本文采用Giesekus黏弹性本构方程和有限体积法离散控制方程,提出了黏弹性流体流动的数值求解方法,并用所发展的数值算法模拟了黏弹性流体在具有不同多边形横截面形状的直管内的二次流现象。然后以正四边形横截面直管为研究对象,分析了二次流的非线性特征,以及二次流产生的涡与流动过程中各物理量的量化关系。

1 理论模型

1.1 控制方程

忽略高分子流体的密度变化,将其视为不可压缩流体,则控制方程简化为:

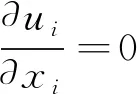
(1)

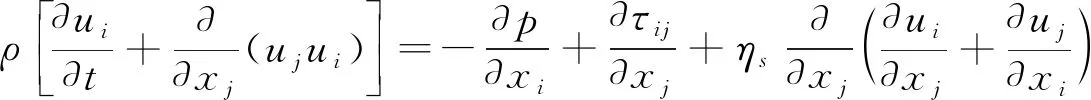
(2)

其中,ρ为高分子流体的密度。

采用Giesekus黏弹性本构方程描述高分子流体的流变行为:

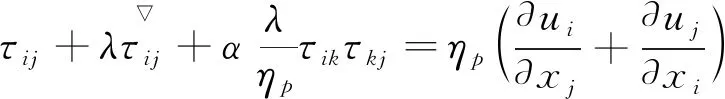
(3)

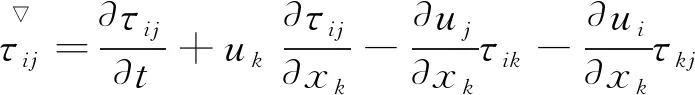
(4)

其中,λ为松弛时间,ηs和ηp为高分子流体和溶剂对零剪切黏度的贡献(η0=ηs+ηp),η为分子流动常数或非线性系数,其取值范围为0≤α≤1。

1.2 边界条件

入口处速度和出口处压力均为恒定值,其他边界采用无滑移无渗透边界条件。对于应力张量的求解,假设初始值为零,即有:

入口:u=u0,τ=0

(5)

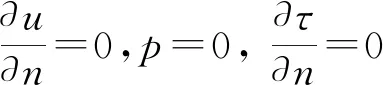
(6)

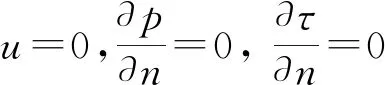
(7)

2 数值算法

本文采用有限体积法离散上文偏微分方程(1)—(3),对速度和压力的求解采用PISO方法,其离散和求解过程见文献[8]。对于Giesekus本构方程,(3)式可化简为:

(8)

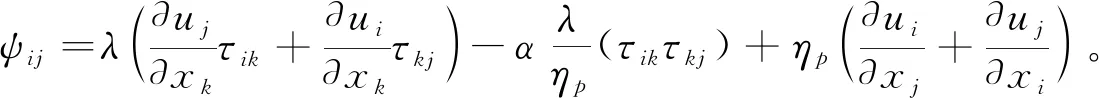
(9)

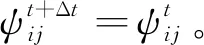
3 结果与分析

3.1 算法验证

采用本文发展黏弹性算法计算了经典4∶1收缩流基准问题,根据文献[10]中的XPP黏弹性参数拟合了对应Giesekus本构方程参数,其中λ=0.314s,η=1360Pa·s,α=0.05,计算了维森伯格数Wi=1和Wi=10时的收缩流。图1为本文算法下流线的模拟结果。从图中可以发现随着Wi数的增大,收缩流的涡亦增大,这和文献[12]中的结果吻合,说明本文所发展的算法能有效计算黏弹性流体的流动。

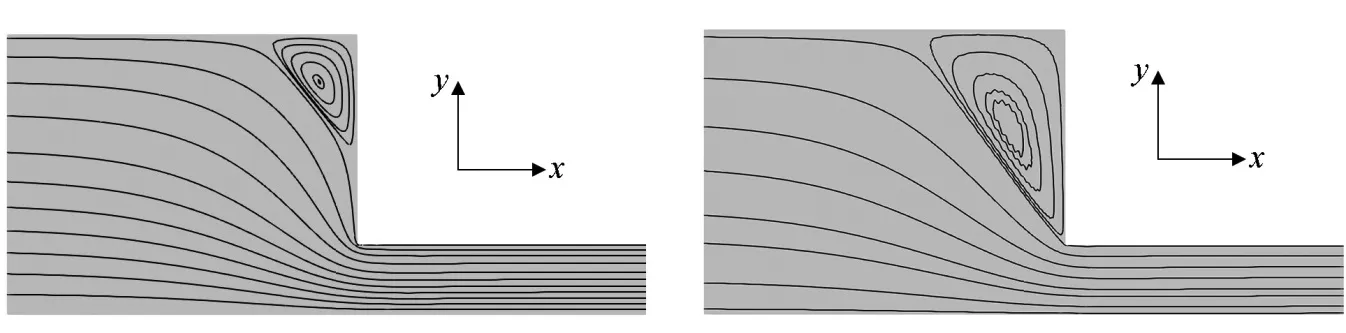
(a) Wi=1 (b) Wi=10

3.2 直管中二次流现象的数值模拟

分别采用内切圆直径为20mm、横截面为等边形、横截面边的个数为3—8个、管长为600mm的直管,黏弹性流体的密度和对应Giesekus参数见表1。入口速度u0=0.2 m/s。

表1 物性参数

图2为不同形状横截面二次流流线分布图。从图中可以发现,多边形直管横截面每条边的两侧均有两个涡,即多边形的每个角两侧均有一个涡。对于二次流的流动,中心处的流体总是向各边中心处流动,各边中心处流体则分别向该边所在的两个端点流动,而各端点处的流体则朝横截面中心处流动。

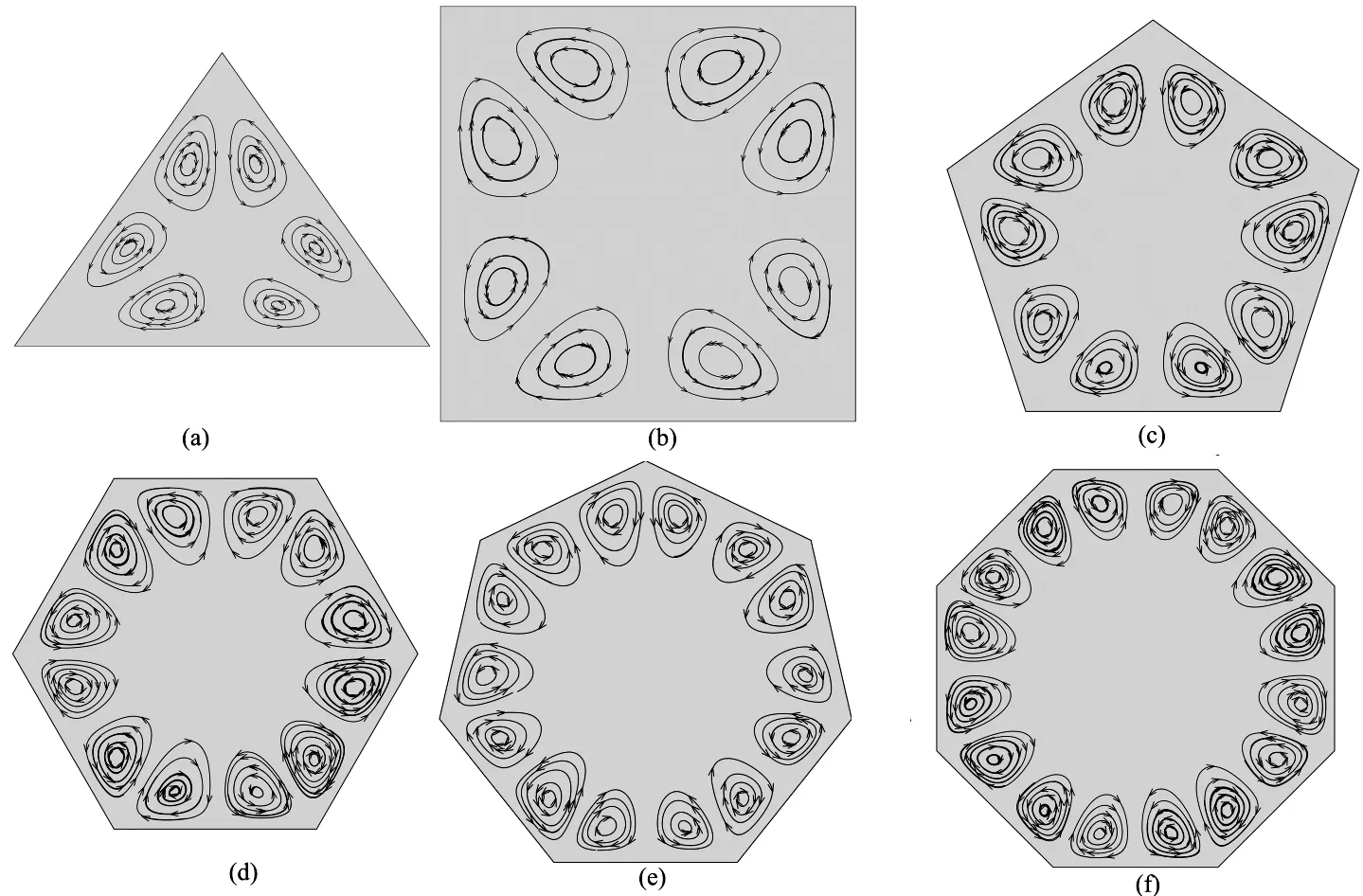
(a)三角形 (b) 矩形 (c)五边形 (d) 六边形 (e) 七边形 (f) 八边形

图2中各横截面的内切圆直径为20mm,且横截面上流线产生涡的个数是边的二倍。所以可以得到对于一个存在内切圆的多边型横截面,假设其边的个数为N,则黏弹性流体在该直管横截面上产生涡的个数为2N。随着N的增大,多边形内角角度就越大,但是其内角小于180°。由于横截面上涡总是沿边和端点分布,所以在内切圆不变的情况下,随着N的增大,边的长度逐渐减小,涡的大小也逐渐减小。当N区域无穷时,边的长度无限趋于零,横截面形状为圆形,涡大小为零,即横截面为圆形时,直管中不会有二次流现象产生。即可以得到,黏弹性流体在圆直管中的流动不会有二次流产生,这和文献[9]的结论一致。

图3为椭圆形直管横截面上二次流流线分布图。从图中可以发现椭圆形直管横截面上二次流会产生四个大小相等对称分布的涡。综合图2和图3可以发现,直管中黏弹性流动的二次流产生受横截面形状的影响,即变曲率的横截面才会产生二次流。和圆形不变的曲率相比,椭圆形的曲率始终会发生变化,所以有二次流的产生。图2中各横截面在顶点处曲率发生变化,所以产生了列于顶点两侧的涡流。

3.3 直方管中黏弹性流体二次流的非线性特性分析

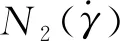
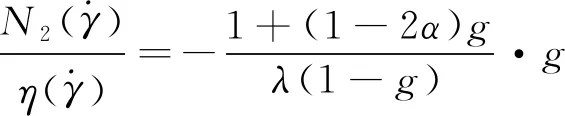
(10)

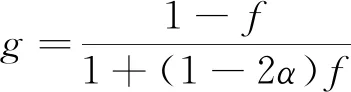
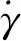
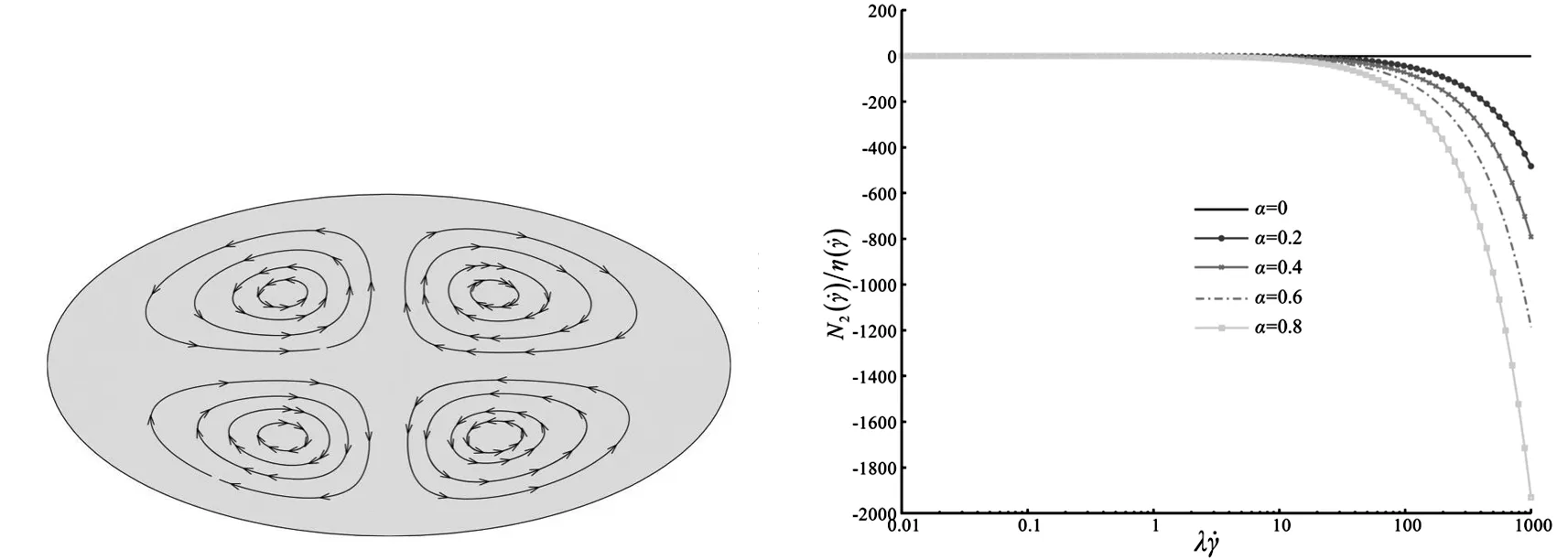
图3 椭圆形直管横截面上二次流流线分布 图4 不同α下和之间关系

为了描述直管中黏弹性流体二次流的非线性特征,以正方形横截面为例,采用上文发展算法,令α=0,模拟了相同条件下黏弹性流体的流动。图5为α=0和α=0.18时直方管横截面上二次流的速度矢量图。可以发现,当α=0.18时,二次流的速度矢量图较好地印证了图2(b)中二次流涡以及流动规律;当α=0时,二次流速度矢量分布由中心点向各方流出,构成了源流。图6揭示了两种情况下过中心点二次流速度大小分布情况。两种情况下二次流速度大小分布均关于形心对称,而且形心处二次流速度均最小。对比主流速度0.2m/s,非线性系数为0.18时,二次流速度约为主流速度的1/103;非线性系数为0时,二次流速度约为主流速度的1/106。所以非零的α极大地增加了二次流的速度。

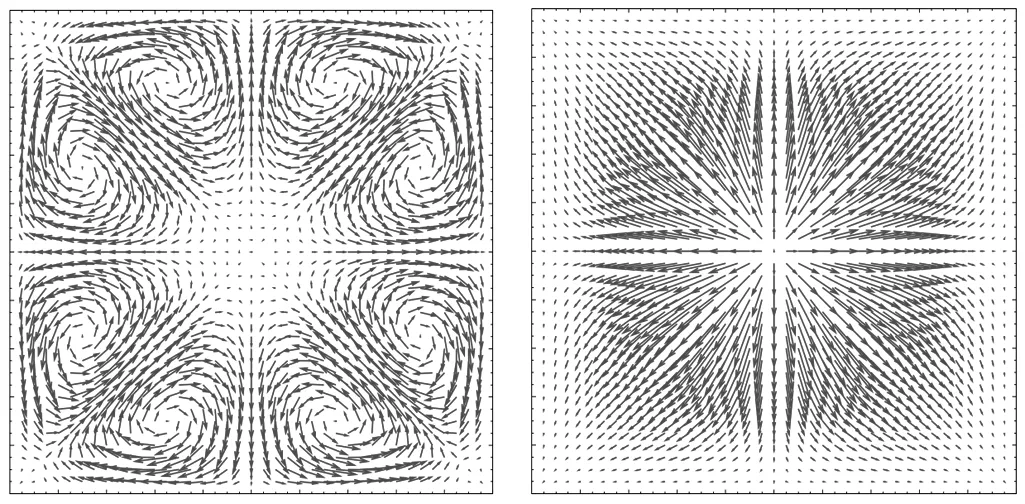
(a) α=0.18 (b) α=0

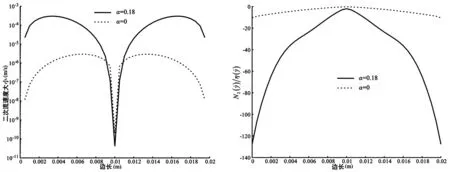
图6 两种情况下过中心点的二次流速度大小分布曲线 图7 两种情况下过中心点上分布对比

4 结论

考虑黏弹性流体的弹性,采用Giesekus黏弹性本构模型描述流体的流变行为,基于有限体积法离散,发展了黏弹性流体流动的数值求解算法,用经典4:1收缩流基准问题验证了所发展黏弹性算法的有效性。模拟了黏弹性流体在不同横截面形状直管内的流动,成功模拟了黏弹性流体由弹性引起的二次流现象,通过数值分析得到以下结论:

(1) 除了流体的弹性特征,直管横截面非恒定的曲率也是二次流产生的重要条件。二次流产生涡的个数是正多边形截面边数的二倍,对于椭圆形横截面直管,二次流产生四个对称的涡。

(2) 黏弹性流体的非线性特征影响二次流,当非线性系数等于0时,直方管中黏弹性流体的二次流为中心点流出的源流,其二次流速度约为非线性系数为0.18时二次流速度的千分之一。

(3) 结果表明,本文所发展黏弹性算法不仅能有效模拟黏弹性流体在直管中流动的二次流现象,而且数值结果所呈现的二次流非线性特性和理论上的非线性特性吻合较好。