考虑表面层厚度不确定的稳健性拓扑优化方法1)

李 冉 刘书田

(大连理工大学工程力学系,工业装备结构分析国家重点实验室,辽宁大连 116024)

引言

拓扑优化[1]是一种基于给定载荷和约束,在特定的域内寻找结构最优传力路径及材料分布的设计方法,具有不依赖于初始构型、设计自由度高及性能驱动的特点,已成为结构与材料创新设计的重要工具[2-5].但由于几何构型较复杂,采用传统的制造工艺往往加工困难.增材制造技术[6-9]是一种通过逐点打印、逐层累积材料来制备结构的新兴技术,可实现高度复杂结构的制备.将拓扑优化方法与增材制造技术相融合,在实现拓扑优化设计价值最大化的同时,还可以充分发挥增材制造的制造潜力,是目前研究的重要趋势[10-11].

但由于制造方式、加工过程及环境、设备和操作等因素的影响,通过增材制造成型的结构件易出现制造缺陷[12-14].制造缺陷使得结构件成型精度降低、表面粗糙度大,进而导致结构件表面材料分布不均匀,引起表面层异质[15].表面层异质会带来结构表面材料属性的不确定性和表面层厚度的不确定性,致使结构性能偏离设计、达不到预期目标.然而,当前大多数拓扑优化方法的研究是基于确定性的参数开展,忽略了不确定因素对结构性能的影响,导致优化后的构型不一定是最优的或者不符合实际,严重影响结构的安全性.因此在拓扑优化设计中,考虑不确定因素对结构构型的影响是十分重要的.

一般来说,考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16-17]和稳健性拓扑优化.其中,基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性,而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度,旨在降低结构性能对不确定因素的敏感程度.近年来,一批学者开展了针对稳健性拓扑优化问题的研究.Asadpoure 等[18]针对桁架结构的随机问题,采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析.Sigmund[19]基于图像形态学中的腐蚀、扩散操作[20]对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟,并在光子晶体波导的稳健性拓扑优化设计中得以验证[21].随后,Schevenels 等[22]通过把离散映射的控制阈值作为随机变量,将该研究扩展到考虑非均匀制造误差的情况.Kang 等[23]基于水平集方法跟踪多材料结构界面的演化,利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析,建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法.针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题,Zheng 等[24]提出了一种基于水平集的稳健拓扑优化方法,采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差.

研究结构表面层异质引起的表面层厚度不确定性,需要解决两个关键问题:(1) 准确识别结构表面层;(2)对不确定性进行传播分析和随机响应估计.本文建立了考虑表面层厚度不确定性的拓扑优化模型,采用基于腐蚀操作的表面层识别技术,实现了表面层异质等效模型的建立.基于摄动有限元法开展了不确定性传播的分析和系统随机响应的预测,并推导了目标函数关于设计变量的敏度信息.通过数值算例证实了考虑表面层厚度不确定性的必要性及本方法的有效性.

1 基于腐蚀操作的结构表面层识别技术

如何准确地对结构表面层进行建模,通常是基于密度的拓扑优化方法中较为困难的问题.Clausen等[25]采用基于两步过滤的操作,以较大的空间密度梯度识别了结构的表面层,并成功应用于基于密度的拓扑优化问题[26-27].本文采用一种基于腐蚀操作的表面层识别技术[28]建立表面层异质的等效模型.其主要思想是:首先对图1(a)所示的初始结构进行腐蚀操作,得到图1(b) 所示规模缩减后的被腐蚀结构;然后将初始结构与被腐蚀结构的不同部分,即图1(c)所示的被腐蚀掉的部分,定义为结构表面层.

图1 基于腐蚀操作的表面层识别方法的基本思想Fig.1 Basic idea of the erosion-based interface identification method

腐蚀操作通过光滑过滤和离散映射两个过程来实现.其中,光滑过滤使得初始结构场光滑连续;离散映射使用一个较大的阈值,将光滑化的结构场进行截断,得到被腐蚀后的结构,进而识别出结构表面层.图2 给出了一维情况下腐蚀操作的一般过程(文中腐蚀操作的所有参数都用下标e 标记).

图2 一维情况下腐蚀操作的一般过程Fig.2 1D example of the general process of the erosion operation

本文中,首先使用基于Helmholtz 偏微分方程的密度过滤[29-30]——PDE 技术[31],对初始结构场µ进行光滑化处理

式中βe为映射函数的锐度,阈值ηe=0.5+Δηe通过引入Δηe∈(0,0.5)来定义.

基于上述光滑过滤和离散映射的腐蚀操作,可以将厚度均匀可控的结构表面层γ 识别出来.表面层厚度w与过滤半径Re、阈值Δηe之间满足如下关系

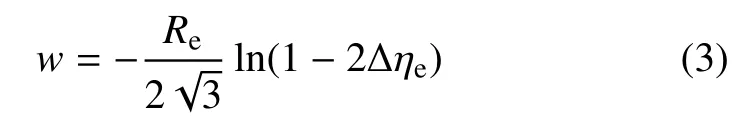
式中,通过合理选取Re和Δηe的值即可实现对表面层厚度w的精确控制.本文采取的策略是固定Δηe的值,通过改变Re的值来控制w.为了得到w和Re更规整的近似关系,文中算例依据经验Δηe均取值为0.45,此时Re≈1.50w.(3)式的详细理论推导参见文献[28].在此基础上,物理密度和刚度的插值函数可以定义为

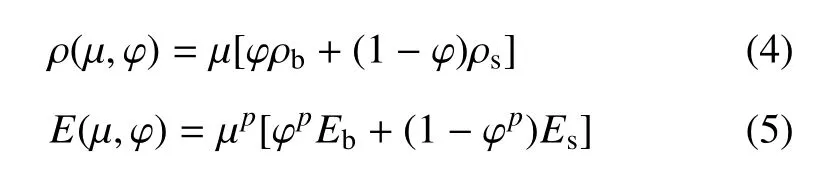
式中ρb,Eb,ρs,Es分别表示基体和表面层的材料性质,p为惩罚因子,一般取值为3.当µ=1 且φ=1时,描述结构的基体部分;当µ=1 且φ=0 时,描述结构表面层;当µ=0 时,表示结构为空.

2 基于摄动有限元的稳健性拓扑优化设计

2.1 摄动有限元法及系统随机响应估计

随机有限元法是将随机分析理论与有限元方法相结合的数值分析方法.其中,基于摄动开展的随机有限元法得到了广泛的应用[18,34-35].其基本思想是:引入一个零均值的微小摄动量Δξ,来描述随机变量ξ 在其均值ξ0处产生微小摄动所引起的不确定性,那么随机变量ξ 可以表示为

若假设系统发生准静态线弹性行为,且不确定性仅存在于某些结构参数(如几何形状、材料性质)中,而外荷载是确定的,那么有限元平衡方程可以写作

式中K(ξ)和u(ξ)分别表示与随机变量ξ 相关的刚度矩阵和位移响应向量.在ξ0处对K(ξ)和u(ξ)进行二阶Taylor 展开

式中K0=K(ξ0),u0=u(ξ0)且Ki,Ki j,ui,uij为K和u在ξ0处对随机变量ξ 的一阶、二阶偏导数.将式(8)、式(9)代入式(7),忽略Δξ 的高阶小量同时合并同阶项,可以得到

通过按自上而下的顺序求解方程组(10),可以得到由式(9)表示的位移响应u的二阶近似表达.若Δξ服从正态分布,那么位移响应u的均值及协方差的二阶近似估计表示为

式中σij=E[ΔξiΔξj]表示Δξ 的二阶统计矩.

2.2 考虑表面层厚度不确定的稳健性拓扑优化方法

本文考虑静力学拓扑优化中的最小柔顺性设计问题,即在确定的外载荷下,给定有限体积的材料,设计得到储存应变能最小的结构拓扑,优化列式可以描述为

式中,设计变量ρe是表示每个单元的密度,c表示结构的柔顺性,K,u,f分别表示结构的总体刚度矩阵、位移向量和外载荷向量,V和¯V分别表示结构所用材料的体积和给定的体积上限.

本文第1 节中,通过基于腐蚀操作的表面层识别技术,对厚度为w的结构表面层进行了建模.本节中以表面层厚度w为随机变量,根据摄动有限元法的思想,引入一个均值为、标准差为σ 且服从高斯分布的微小摄动量δ,对表面层厚度的不确定性进行建模.稳健性拓扑优化设计旨在优化结构的性能,并且最小化其对不确定因素的敏感程度.那么,考虑表面层厚度不确定性的稳健性拓扑优化列式可以描述为

那么,结构柔顺性均值E[c]、方差Var[c]的近似估计可以表示为

3 数值算例

为了避免棋盘效应和网格依赖性对优化结果的影响,并保证得到0-1 分布的结构场,在识别结构表面层之前,先后对初始结构场应用了PDE 过滤、基于Heaviside 过滤和tanh 函数的离散映射.这一过程与基于腐蚀操作的表面层识别几乎相同,但却实现了不同的功能.文中将这一过程定义为过滤过程(所有参数都用下标f标记),将表面层识别的过程定义为腐蚀过程,并将过滤过程和腐蚀过程统称为改进的两步过滤法,其实现流程及控制参数见图3.此外,所有算例都使用鲁棒公式[19,21-22]来实现结构最小尺寸的控制,控制参数[28]为Δηf;同时通过域扩展方法[37]保证在结构边界处获得相同的腐蚀厚度.

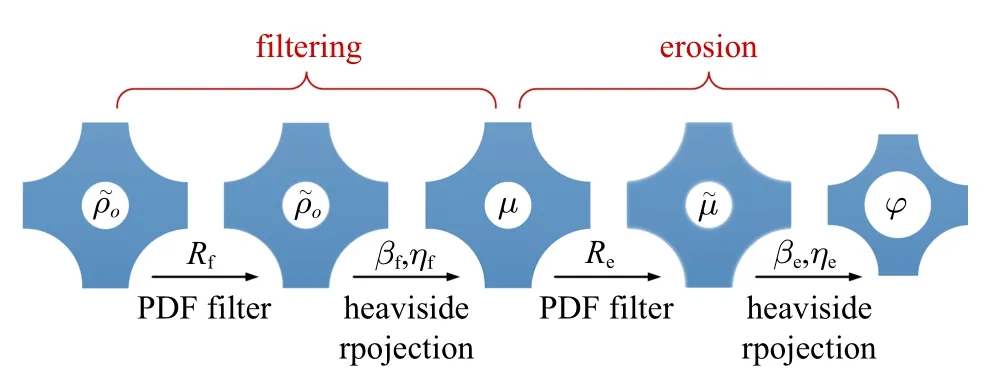
图3 改进的两步过滤法识别结构表面层Fig.3 Improved two-step filter process for structure surface layer identification

本文算例中数值为常量的控制参数如下:惩罚系数p=3;当计算收敛时或每50 个迭代步后,投影锐度βe=βf∈(1,20)变为当前值的1.5 倍.

3.1 简支梁算例

图4 所示为简支梁算例的设计域及边界条件,结构的几何尺寸为300 × 150,集中力F=1.表面层结构和基体结构的材料属性分别为ρs=1,Es=1,ρb=0.8,Eb=0.5,即表面层为硬材料,基体为软材料.表面层厚度为w=2,其标准差σ=0.3w.过滤过程和腐蚀过程的过滤半径分别取值为Rf=8,Re≈1.5w,最小尺寸的控制参数Δηf=0.1.体积分数为40%且每10 个迭代步进行一次更新[28].目标函数中的权系数α 选取值为4.

图4 简支梁算例的设计域及边界条件Fig.4 Design domain and boundary conditions of MBB example

如图5 所示,简支梁结构的确定性和稳健性拓扑优化结果有着不同的拓扑构型,相比于确定性设计,稳健性设计去除了细小孔洞的存在.不同结果对应的结构柔顺性均值和标准差数值,列入表1.与确定性设计相比(σ=3.952 8),稳健性设计(σ=3.383 3)的标准差较小,这表明稳健性拓扑优化结果对表面层厚度变化的敏感性更低.图6 给出了确定性设计和稳健性设计在优化过程中目标函数和体积分数的迭代历史,最后都达到了稳定收敛.

图5 简支梁算例的拓扑优化结果Fig.5 Topology optimization results of MBB example

表1 确定性设计和稳健性设计结果的对比Table 1 Comparision of deterministic and rubost solutions

图6 简支梁算例目标函数和体积分数的迭代历史Fig.6 Convergence history of objective function and volume fraction of MBB example

为了研究目标函数中权系数α 的取值对拓扑优化结果的影响,本文比较了当α 分别取值为2、4、6时,表1 中列出了稳健性设计下结构柔顺性的均值和标准差的数值,图7 所示为相对应α 取不同值时结构柔顺性的均值与标准差的变化趋势.可以看出结构柔顺性的均值随着权系数α 的增大而增大,但其标准差却呈现出相反的变化趋势,这与双准则优化问题帕累托解的基本特征是吻合的.同时,标准差越小反映出结构对不确定因素的敏感程度越低.

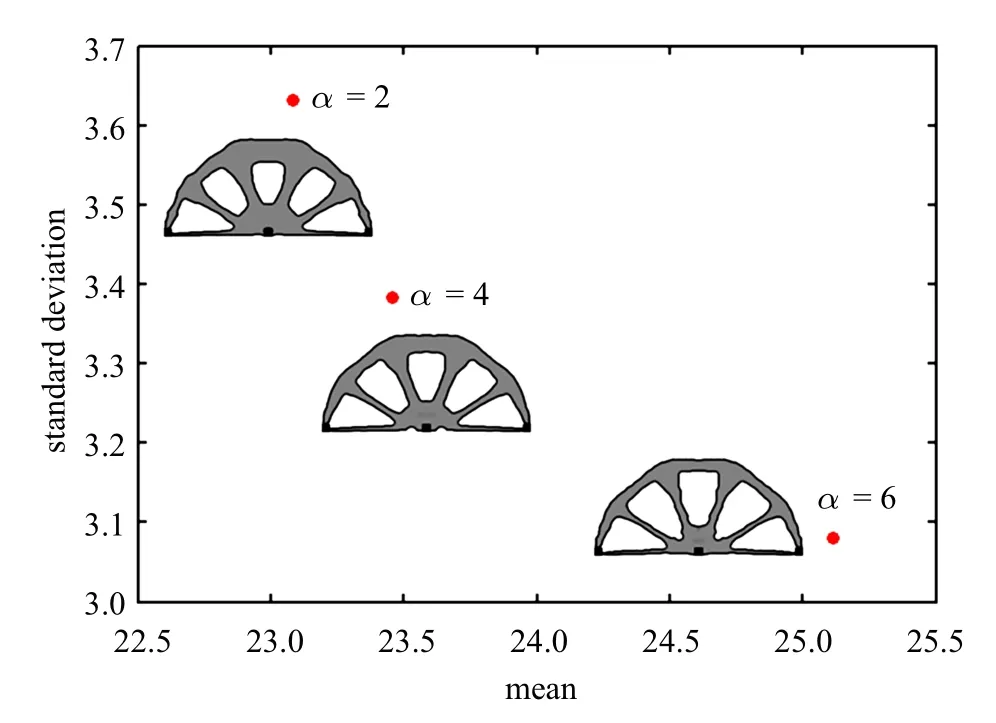
图7 权系数α 取不同值时结构柔顺性的均值与标准差Fig.7 Mean and standard deviations of compliance for different weighing factor α

3.2 悬臂梁算例

图8 所示为悬臂梁算例的设计域及边界条件,结构的几何尺寸为300×100,集中力F=1.表面层结构和基体结构的材料属性分别为ρs=0.7,Es=0.4,ρb=1,Eb=1,即表面层为软材料,基体为硬材料.表面层厚度为w=2,其标准差σ=0.05w.过滤过程和腐蚀过程的过滤半径分别取值为Rf=8,Re≈1.5w,最小尺寸的控制参数Δηf=0.1.体积分数为40%且每10 个迭代步进行一次更新.目标函数中的权系数α 选取为1.

图8 悬臂梁算例的设计域及边界条件Fig.8 Design domain and boundary conditions of cantilever beam example

结构的确定性和稳健性拓扑优化结果如图9 所示,相比于确定性结果,稳健性结果去除了细小杆件的存在,且结构表面更为平滑.表2 所示为σ 取不同值时确定性设计和稳健性设计结果对比.从表2 可以看出,稳健性设计的标准差较小,其均值和标准差的加权和值也更低,再次验证了稳健性结果在结构整体刚度较高的同时具有更好的抵抗不确定性的能力.优化过程中目标函数和体积分数的迭代历史如图10 所示,都达到了稳定收敛.

图9 悬臂梁算例的拓扑优化结果Fig.9 Topology optimization results of cantilever beam example

图10 悬臂梁算例目标函数和体积分数的迭代历史Fig.10 Convergence history of objective function and volume fraction of cantilever beam example

本文研究了当表面层厚度标准差取不同值时,对稳健性拓扑优化结果的影响.在其他参数保持不变的情况下,σ=0.05w,σ=0.2w,σ=0.3w所对应的稳健性拓扑优化结果分别如图9(b)、图11(a)、图11(b)所示.可以看出,当不确定性相对较小(σ=0.05w)时,稳健性设计与确定性设计有着相似的结构;而在σ=0.2w,σ=0.3w的情况下,稳健性结果与确定性结果在杆件数量、布局等方面具有一定的差异.3 种情况下结构柔顺性的均值和标准差的数据比较见表2.数据表明,任一情况下稳健性设计结果的标准差值、均值和标准差的和值都小于确定性结果,进一步验证了本文所提出方法的有效性.

表2 σ 取不同值时确定性设计和稳健性设计结果的对比Table 2 Comparision of deterministic and rubost solutions for different σ

图11 σ 取不同值时悬臂梁算例的稳健性拓扑优化结果Fig.11 Robust topology optimization results of cantilever beam example for different σ

4 结论

针对增材制造工艺在制备过程中出现的结构表面层异质现象,本文以结构柔顺性均值和标准差的加权和作为优化目标,建立了考虑结构表面层厚度不确定的稳健性拓扑优化模型.采用一种基于腐蚀操作的表面层识别技术对表面层异质进行了等效建模,并将表面层厚度视为具有给定概率分布特征的随机变量,通过随机摄动理论开展了不确定性传播分析和系统随机响应预测.数值算例表明,所提出的方法能够得到对结构表面层厚度变化不敏感的合理结构,具有更强的抵抗不确定性的能力.因此,对增材制造结构而言,在拓扑优化设计中考虑表面层厚度不确定性对结构性能的影响具有重要意义.