基于假设检验理论的统计分辨研究综述
张云雷, 李 轲, 卢建斌
(海军工程大学电子工程学院, 武汉 430033)
对近邻目标进行跟踪或识别时,往往需要对同一分辨单元两个或多个目标进行分辨,因此近邻目标的高分辨在雷达[1-3]、水声[4]、光学[5-6]、频谱分析及阵列信号处理[7-8]等领域获得了广泛关注。
Woodward[9]最早提出了模糊函数的定义,并讨论了幅度相等、具有一定多普勒频移和距离延时差异的两个波形的距离和多普勒分辨率极限,指出两个信号的相关系数对分辨能力有直接影响,相关系数越小越容易分辨。根据Woodwald[9]的定义,距离分辨力定义为同一方位不同距离上两目标能够分开最小间隔。距离分辨力δR采用模糊函数来衡量,定义为其响应功率下降到1/2时对应的距离间隔,取决于信号的带宽,δR=C/(2B),其中,C为光速,B为信号带宽。方位分辨力δA为区分两方位上两近邻目标的能力,定义为波束响应功率下降到1/2对应的方位间隔,与天线孔径(D)和工作波长(λ)有关,可表示为δA=kλ/D,其中k为常数。文献[10]进一步将模糊函数分辨推广到角度域,并设计了距离、速度、方位和俯仰四个维度的最大似然估计器。
上述定义未考虑实际系统噪声和杂波的影响,称为固有分辨率或名义分辨率。实际使用中存在的问题有:一是难以衡量瑞利限内目标,即超分辨性能。随着高分辨空间谱估计算法的不断出现,对超瑞利限算法的性能评价需求迫切;二是该方法定义的分辨限是固定值,不能反映随机因素的影响。实际系统受到噪声和杂波的影响,单次分辨与否并不确定。因此学者提出应该把分辨问题看作统计问题,并提出统计分辨的概念。关于统计分辨的研究通常围绕两方面:一是给定虚警概率和分辨概率,系统可达的可分辨最小统计距离,称为统计分辨限(statistical resolution limit,SRL)。该值反映了观测数据质量的影响,如信噪比、信号相关性等参量。二是给定两信号的参数间隔和信噪比、虚警概率等参数,研究系统可达的最大分辨概率。
文献[11]基于相关分析,讨论了随机噪声影响下的统计分辨限的大小,分析了噪声对分辨概率的影响,但该方法不适用于超瑞利限分辨。文献[12-13]将瑞利限扩展到两个非等强目标的分辨,但未考虑噪声等随机因素的影响。
文献[14]从空间谱响应角度,给出高分辨空间谱分辨能力的定义。假定空间谱响应函数P(θ),两待分辨参数之间的间隔为D=|θ1-θ2|,定义中间参数的响应为Pm=[P(θ1)+P(θ2)]/2,判断两个待分辨谱响应的平均值与中间值的响应的差Q(D)=Pm-P[(θ1+θ2)/2],大于0则两信号可分辨,否则不可分。基于以上定义,文献[15]研究了MUSIC(multiple signal classification)谱估计算法的统计分辨性能,文献[16]研究了AR(auto-regression)谱估计算法的统计分辨性能。然而,该类算法只能针对特定谱估计算法,并不具有推广性。

近年来,有学者开始采用假设检验理论来定义统计分辨限,其思路如下:通过将分辨问题建模为二元假设检验(binary hypothesis testing,BHT)模型,零假设代表只存在1个目标,而对立假设代表存在2个目标。通过求解分辨统计量及其分布,可以定量分析统计分辨概率或SRL的大小。采用假设检验的研究方法和检测问题实际上是相同的,如表1所示。对于检测问题,研究在给定虚警概率下能够达到的检测概率,采用NP(Neyman-Pearson)准则构建最优检测统计量。对于分辨问题,研究给定虚警概率下可达的分辨概率,采用广义似然比(general likelihood rate test,GLRT)求解统计量,即对未知参数进行最大似然估计然后代入分辨统计量求解,然后得到分辨概率和虚警概率的关系。
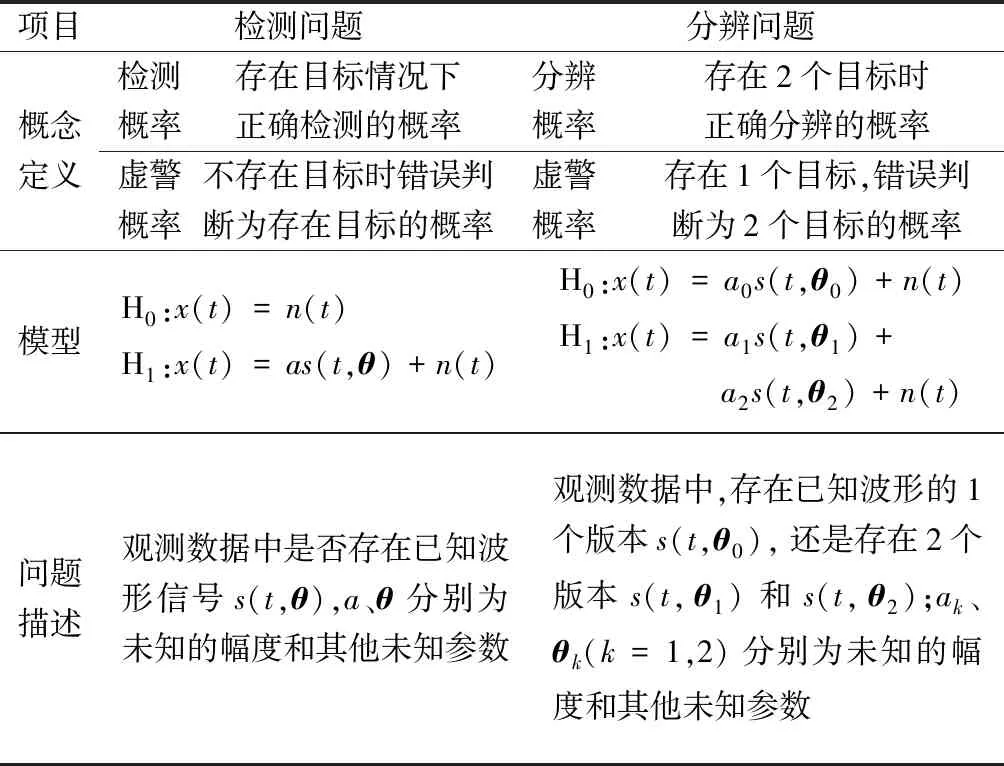
表1 基于BHT的检测和分辨问题的相似性
相对于基于估计的定义方法,基于假设检验的方法能够定量讨论影响SRL大小的因素,且容易扩展到多维空间,因此得到了学者们的重视。
基于假设检验理论进行统计分辨的研究具有很长的历史。早在20世纪60年代,Root[1]就针对瑞利限内目标多个参数的分辨问题,建立了BHT模型。Nilsson[32]针对近距离目标的检测和估计联合问题,设计了联合考虑信号数目误差和精度误差的代价函数。Ksienski等[3]对瑞利限内两近邻角度参数分辨,基于Root假设检验对最大2个目标情形进行理论探讨,指出了相位差对分辨性能的影响。Trunk[33]首先将方法引入到雷达距离分辨中,讨论了距离上进行统计分辨的重要意义,仿真讨论了采样位置和相干积累对分辨性能的影响。可以看出,早期的瑞利限内分辨问题研多是理论上探讨,未能求解统计分辨限的解析表达式。
现围绕该问题开展研究综述,通过梳理基于假设检验的统计分辨模型和分辨统计量求解方法,得到该类问题研究的一般思路:构造二元假设检验模型,利用泰勒近似得到关于待分辨参数的线性模型,或利用大快拍数条件渐近分布,求解统计量的分布,进而得到统计分辨限与波形、信噪比等参数的解析关系,从而得到进一步的研究方向。
1 基于假设检验的统计分辨研究现状
21世纪以来,随着统计信号处理的快速发展,基于假设检验的统计分辨研究重新得到重视。当前基于假设检验的统计分辨研究主要包括内容如下。
1.1 单个维度上的统计分辨
在频率维方面,文献[34]研究了白噪声条件下两正弦信号的统计分辨性能,假定分辨中心频率已知,而幅度和相位未知。由于观测和待分辨参数高度非线性,通常采用泰勒展开近似得到线性模型,进而求解分辨统计量分布及其性能,得出分辨信噪比与可分辨频率间隔和带宽乘积的4次幂成反比,因此在信号带宽给定情况下,信号可分辨频率间隔随着信噪比增加理论上来说可以无限小。由于阵列信号处理中的方位等价于接收到的角频率,所以基于频率的研究可直接扩展到方位维分辨。
针对点源目标方位分辨,通常假设目标回波幅度或者接收波形未知,此时的GLRT方法为渐近意义上的最优检测器。GLRT方法首先对未知参数或波形做最大似然估计(maximum likelihood estimator,MLE),然后进行似然比检验。基于该思路,文献[35]采用一阶泰勒展开近似得到关于待分辨参数的线性模型和GLRT方法,研究了存在方位点源干扰条件下被动线阵对两目标的方位角度的SRL,分析了波形已知/未知、噪声已知/未知等多种情形,得出SRL与信噪比、波形等均有关系。文献[36]将上述研究扩展到二阶泰勒展开近似模型。针对待分辨中心参数未知的情形,文献[37]首先求得未知中心角度参数的MLE然后进行分辨,得到未知待分辨中间参数时角度SRL的性能损失;文献[38]讨论了单基地MIMO雷达中近邻目标的方位统计分辨问题,得出噪声方差已知/未知情况下的信噪比(signal noise rate,SNR)的表达式。文献[39]讨论了超宽带随机信号下的圆环阵列对空间角度邻近目标的角度SRL。文献[40-41]进一步将其扩展到随机噪声MIMO雷达,推导了在给定虚警概率和检测概率时宽带MIMO雷达的统计角分辨力表达式,分析了检验参数、信噪比、目标参数以及MIMO雷达发射波形参数和几何参数对分辨力的影响。
关于距离维SRL研究方面,文献[42-44]讨论成像领域的距离统计分辨,假定距离维的响应函数,采用泰勒展开近似得到线性模型求解问题,得到距离统计分辨能力与波形、采样频率和信噪比的关系。文献[45]基于脉压前的原始回波进行类似的分析,得到分辨性能与波形的表达式。
上述研究均采用泰勒展开近似,也有文献采用渐近分布求解。文献[46]研究圆环阵对空间两近邻点源目标的统计分辨问题,利用GLRT的渐近分布,得到存在多个未知参数条件下的检测统计量为卡方分布,并指出了基于假设检验定义的SRL和基于估计定义的SRL之间的联系,指出参数p和一组特定的分辨概率和虚警概率相关。
1.2 多维统计分辨的扩展
和基于估计定义的分辨研究相类似,基于假设检验定义的统计分辨研究也被扩展到多维。文献[47]讨论了多维SRL的定义,并指出了与估计定义的多维SRL之间的关系。文献[48]研究了基于BHT的近场两信源的角度和距离联合统计分辨,得出了信号相关性与阵列配置的影响。文献[49]讨论噪声功率已知/未知条件下的MIMO雷达对近邻目标的DOA(degree of arrival)和DOD(degree of departure)二维联合分辨,并对比了透视检测器的性能。文献[50]在上述研究的基础上考虑子空间干扰对分辨限的影响。文献[51]进一步考虑了多普勒频率在内的三维统计分辨性能。文献[52]讨论宽带噪声MIMO雷达的空间的距离SRL,指出了x和y联合维度的分辨限可以表示为一个椭圆。文献[53]针对单个阵元,讨论了距离-脉内多普勒二维统计分辨限的表达式,指出了联合分辨限是距离和多普勒维的权衡。文献[54]针对线性阵列,讨论了角度-脉间多普勒的空-时二维联合统计分辨限。文献[55]进一步将上述研究扩展到距离-方位-脉内多普勒三维的分辨情形。
1.3 理论工具的扩展
文献[56]针对极化阵列讨论对比了采用假设检验方法与贝叶斯、信息论方法的角度SRL的性能。文献[57]应用信息论准则来研究线性阵列对角度SRL,得到待分辨中心参数未知时统计量分布以及SRL表达式。文献[58]针对二维距离统计分辨,利用KL(Kullback-Leibler)距离建立了基于假设检验定义的SRL与信息论定义的SRL之间的联系,讨论了欠采样和模型失配时的性能损失。针对H1条件下对未知参量MLE估计的计算量大的问题,文献[59-62]采用Rao检测进行分辨,与GLRT方法在渐近条件下具有类似的性能。
1.4 关于SRL的应用研究
文献[63]对比了时分复用MIMO雷达和常规MIMO雷达的角度SRL性能。文献[64]将SRL研究应用到超声领域,得到分辨限与高斯调频信号带宽、载频、调频率和相位的关系。文献[65]讨论了时间反转MIMO雷达的角度SRL的表达式,在不同噪声条件下,与常规MIMO雷达的SRL相比各有优劣。
2 基于BHT的统计分辨模型
基于假设检验的统计分辨研究,应用的前提是待分辨单元很小,同一分辨单元内仅存在1个或2个目标,通过构造0-1假设检验模型,将分辨问题建模为BHT问题,零假设表示存在1个目标,对立假设表示存在2个目标。以文献[36,57]的线阵阵列模型为例,讨论方位上的分辨建模方法。
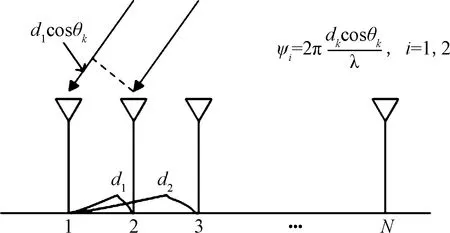
dcosθk为相邻阵元中间的波程差;Ψi为波程差引起的 相位差;λ、θk分别为电磁波传播波长和来波相对基线方位角图1 线性阵列角度分辨示意图Fig.1 Sketch map of the angle resolution for the linear array
图1给出了一维线性阵列对近邻空间信源的角度分辨示意图,以第一阵元未知为相位参考,假定N阵元数位置矢量d=[0,d1,d2,…,dN-1]T∈RN×1。
已知两远场窄带信号s1=[s1(1),s1(2),…,s1(L)]T和s2=[s2(1),s2(2),…,s2(L)]T,回波的波形幅度和相位未知,其中,L为快拍数,sk∈CL×1,k=1,2。则第l个快拍时刻的观测数据可以表示为
x(l)=v(w1)s1(l)+v(w2)s2(l)+n(l)=
v(w0-δ1)s1(l)+v(w0+δ2)s2(l)+n(l)
(1)
式(1)中:δk(k=1,2)为w1和w2与待分辨中心w0的距离;n(l)为噪声信号;v(w1)和v(w2)为两目标信号的阵列导向矢量,其表达式为
v(wk)=[1,ejwkd1,ejwkd2,…,ejwkdN-1]T
(2)
将L个快拍数据排列成列矢量,则得到观测向量为
x=V1s1+V2s2+n
(3)
式(3)中:V1=IL⊗v(w0-δ1);V2=IL⊗v(w0+δ2),均为与导向矢量相关的矩阵,IL为L×L的单位矩阵;v的定义见式(1)、式(2);n~CN(0,σ2INL)为加性白高斯噪声,其中,CN表示复高斯分布,σ2为噪声功率。
综上,可以构建关于待分辨参数的二元假设检验模型为
(4)
假设H0表示只有一个信号s0,其中前面乘上了和导向矢量相关的表达式V0=IL⊗v(w0),而假设H1表示存在两个信号,则式(4)可以等价为
(5)
式(4)中观测数据为待分辨参数ω的非线性函数,求解比较困难,需要寻找近似或者等价方法求解。
上述内容讨论的是方位上的统计分辨模型。实际上,可以建立包括距离、多普勒和方位等联合维度的统计分辨模型。对于雷达等主动传感器来说,如果考虑脉内多普勒的影响,则距离和多普勒是存在耦合的[53,55]。
3 检测统计量及其分布
建立基于BHT理论的统计分辨模型[式(4)]。为得到统计分辨性能,需求解检测统计量及其分布。通常分为两种思路:一类利用泰勒展开近似将该问题转化为关于待分辨参数的线性模型[53,55,58],然后利用GLRT方法求解;文献[45,48-50]利用投影定理将分辨问题转化为检测问题再利用GLRT求解,线性模型下可得到精确分布。另一类利用大快拍数据下的渐近分布求解[46,66]。该方法不受到未知变量和分布的限制,但需要足够的数据采样。
3.1 利用线性模型直接求解
针对回波对于待分辨参数高度非线性,通常的思路是,利用两信号分辨参数差异很小,将上述两个方位的回波信号在估计参数中心w0=(w1+w2)/2处进行泰勒展开,保留其一阶或二阶近似,得到关于待分辨参数的线性模型。
具体来说,将式(3)中的观测信号在其导向矢量相关矩阵V0处进行泰勒一阶展开并近似,并定义为
(6)
式(3)转化为关于分辨参数的线性模型为
(7)

(8)
对于距离分辨来说,此时的待分辨参数不再是角度而是时间。文献[45]假定主动阵元发射信号为s(t),两接收信号α1s(t-t1)+α2s(t-t2),其中α1和α2为两目标回波的幅度。进行泰勒展开近似并保留一阶项,若时间采样点数为L,则可建立基于BHT理论的距离分辨矢量模型为
(9)

方位维和距离维分辨模型,经过泰勒展开近似后,均可以写为关于待分辨参数的线性模型。对于方位分辨来说,信号波形出现在未知参数θ中,如式(8)所示,而对于距离分辨来说,信号波形出现在系数矩阵中,如式(9)所示,这是因为分辨的对象不同所致。
(10)
式(10)中:选择矩阵A∈Rr×p,满足rank{A}=r,其中前r列为全零向量,后s列构成单位阵。
线性模型的检测统计量为
T(x)=2lnLG(x)=
(11)
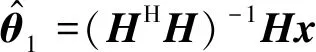
(12)
式(12)中:χr为自由度为r的中心卡方分布;χ′r为自由度为r的非中心卡方分布;卡方分布的自由度为未知参数的个数,而非中心参数为
(13)

(14)
进一步写为
(15)
式(15)中:θ=s-,为常见的检测模型,可以直接利用检测理论得到统计量的分布。
3.2 利用大快拍条件求渐近求解
参见文献[67],当数据记录很大而信号相对较弱时,观测数据的最大似然估计收敛到真实的概率分布,此时二元假设检验模型为
(16)
式(16)中:θr和θs分别为待检验参数和多余参数,含义见式(10),其对数似然比服从渐进分布:
(17)
此时非中心参数为
(18)
式(18)中:I(θr,θs)为Fisher信息矩阵; [I-1(θr,θs)]rr|θr=0为待估计参数对应的分块矩阵。
4 展望
基于假设检验理论的统计分辨研究可以揭示统计分辨限与给定的虚警概率、检测概率的关系,可以是单个维度,也可以是联合维度。结合最近出现的新动态,认为以下方向还值得进一步研究。
4.1 非理想研究条件扩展
当前研究均考虑理想模型(待分辨中心方位精确已知、不存在阵列误差等),文献[58]讨论了点响应函数存在偏差时,统计分辨误差。文献[26]讨论了阵列流型矢量存在误差时,利用Smith定义的SRL的渐近性能。文献[68]讨论了分辨中心参数服从高斯分布时,研究了和方位SRL紧密相关的参数Chornoff上界(Chornoff upper bound,CUB)的变化。除了上述非理想情况,实际中非理想情况还包括分辨中心为某一范围、距离分辨问题中不同采样位置等的影响。
4.2 目标随机/无条件下的统计分辨研究
以上基于假设检验的统计分辨研究,均采用确定未知模型,又称为条件(conditioned)模型。对于雷达传感器来说实际的目标回波为随机分布。在随机分布假设下,基于估计理论定义的SRL研究见文献[21,23]。在假设检验定义方面的研究较少,其中文献[69]基于贝叶斯准则研究了两近邻目标理论上可达的角度下限。文献[70]则讨论了随机分布假设下目标的距离维SRL。
4.3 研究方法的使用边界
从第3节可以看出,两种研究思路均有适用条件,采用泰勒展开近似需要分辨间隔足够小,而渐近分布需要足够大的快拍数。为保证两种求解方法的性能,需定量计算近似误差或快拍数对分辨性能的定量影响,但尚未见相关的研究报道。该问题从理论上定量分析可能存在解析困难,可以通过仿真来研究。
4.4 已知目标个数下的参数估计问题
与匹配滤波或MUSIC高分辨谱估计等算法不同,基于假设检验的统计分辨研究只能给出目标个数信息,并不能求解目标的位置。在已知目标数条件下,如何对瑞利限内的多个目标的参数位置进行估计值得研究。该方面的研究角多,可以参考多元假设检验[71]或各种超分辨的算法[72]。
4.5 基于最优分辨的波形设计问题
基于BHT模型,可得到分辨概率或SRL的解析表达式,进而开展最优分辨的波形设计。基于该思路,文献[73]研究了存在方位干扰下MIMO雷达的最优分辨的波形设计问题,还可进一步扩展到针对距离、多普勒分辨的最优波形设计。
5 结论
基于假设检验定义的统计分辨研究具有理论成熟、方法直观的特点,利用该方法的结论可确定基于估计统计分辨定义中,参数p与分辨概率、虚警概率的关系。该研究有助于理解统计分辨的概念和其影响因素,为设计更高分辨系统提供了借鉴。

