波状前缘叶轮对轴流式水力机械水力性能的影响

夏伟鹏，郭志伟

（武汉大学水利水电学院，武汉430072）

0 引 言

轴流式水力机械的应用十分广泛，如应用于农业输水和城市排涝的轴流泵［1，2］。轴流式水力机械实际运行情况十分复杂，在偏离设计工况运行时，轴流式水力机械的水力性能会明显降低，国内外学者针对此进行了大量研究。学者们研究发现流场对轴流泵有着重要的影响，导叶对泵出口流态起着重要作用。导叶可以显著减少出口回流和漩涡，改善轴流泵出口流态，减少能量损失。同时发现，针对不同工况，可以通过调节后置导叶叶片安放角，改变导叶出口流体速度，从而达到最优旋流要求，提高轴流式水力机械的水力性能［3-8］。在轴流式喷水推进泵中，同样发现进水不均匀和间隙等均会严重影响轴流式喷水推进泵水力性能［9-11］，进水不均匀在进水管和导叶中引起大量的能量损失，并且在导叶后缘附近观察到明显的流动分离，从而会降低轴流式喷水推进泵的扬程和效率。因此，不同轴流式水力机械内部流动均会对泵的扬程和效率产生明显的影响，采用有效的设计技术对轴流式水力机械性能尤其是偏离设计点的性能有着重要指导意义。

轴流式水力机械的核心做功部件是叶轮，当前改善轴流式水力机械水力性能的主要措施很少与叶轮密切相关。近些年，人们开始从大自然寻找灵感，应用仿生技术来解决工程问题。Fish 等［12，13］发现座头鲸鳍的波状前缘起到增强升力装置的作用，控制鳍状肢上方的流动，并在大攻角下保持升力，使其具有高度的机动性。Miklosovic［14］通过风洞测量表明，在理想座头鲸鳍的比例模型中增加波状前缘，可以增加升力和减小阻力，并且使失速角延迟约40%。Johari 等［15］采用不同的波长和波幅的波状前缘NACA 634-021 翼型实验，发现波状前缘会减小翼型的最大升力系数，但在失速时，翼型时速更加平缓，且升力系数提高了50%。Weber 等［16］人发现波状前缘的槽底会产生涡流，可以帮助维持水流附着在边界层，延迟失速到更大的攻角，增加升力，并减少阻力，并将其应用到各种海洋技术上，包括帆船桅杆、风扇、螺旋桨等。波状前缘对水翼流场的影响和形成机理被重点研究，结果表明，波状前缘引起了压力梯度和涡的形成，这可能是失速角延迟的原因［17-20］。WEI Z Y 等［21］对波状前缘水翼研究发现，由于与边界层厚度相对应的高度，结节起到涡流发生器的作用，波状上产生了流向相反的涡旋对，并减轻了流动分离。郭志伟等［22］研究了波状前缘导叶对水泵水轮机性能的影响，发现波状前缘导叶的应用有效地改善了水轮机驼峰的特性。仿生技术逐渐成熟，应用波状前缘已经成为一种解决工程问题的可行技术手段。

本文以轴流式喷水推进泵为研究对象，结合仿生思想，研究了波状前缘叶轮对轴流式水力机械的水力性能的影响。对比了不同工况下原型喷水推进泵和波状前缘叶轮喷水推进泵的水力性能，通过分析内部流动和熵产分布，阐明了波状前缘的影响特征，并进一步探讨了波状前缘叶轮对轴流式水力机械水力性能影响的机理。研究成果同样可为提高农业用水及城市排涝效率的轴流式水力机械提供新的设计理念。

1 数值计算方法

1.1 计算区域

参考轴流式叶轮设计［23］，建立了如图1的计算域。入口和叶轮外壳直径D均为304.8 mm，转子顶部间隙为0.508 mm。出口段直径为0.7D，叶轮和导叶分别有6 个和8 个叶片。在性能测试过程中，在进口段和出口段分别设置了监测站，监测了进口站和出口站之间的流入和流出信息，计算区域的长度沿Z 轴约为3D。

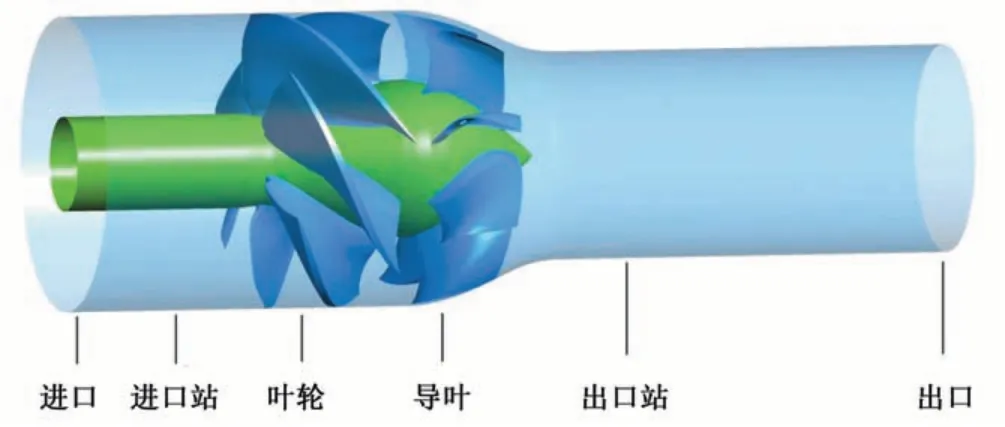
图1 轴流式喷水推进泵的计算区域Fig.1 Computational domain of the axial flow waterjet pump.

无量纲参数流量系数（Q*）、水头系数（H*）和功率系数（P*）定义为：

式中：QV为通过泵的体积流量；n为每秒转数（按1 400 r/min 转速计算）；D为进口直径；ρ为水密度；PIS和POS分别为进口站和出口站的总压力；Tr为叶轮扭矩。

泵效率η可通过以下公式计算：

1.2 波状前缘叶轮设计

基于仿生水翼设计波状前缘翼型的方法设计了波状前缘叶轮［21］，翼型展向各个截面相同，但叶轮和翼型不一样，波状前缘叶轮需要在展向不同叶高截面进行变换。

根据先前对带有波状前缘的翼型的研究，波数可选择设置为2/s，4/s，8/s，s为叶轮叶片展项长度。振幅设置为0.025C、0.05C和0.12C，其中C为叶轮叶片的平均弦长，这些振幅与座头鲸鳍的数据相关［19］。为了研究波数和振幅的影响，我们设计了5个具有不同的波状前缘叶轮（图2）。

1.3 湍流模型

本文采用ANSYS Fluent求解，其控制方程如下：

目前使用的二方程模型都缺乏一个基本的精确输运方程，这一缺陷的原因在于，精确方程ε并没有描述大尺度，而是描述耗散尺度。Egorov and Menter 基于Rotta 模型提出了一种改进的湍流模型长度-尺度方程，模型的这一特性被称为“尺度自适应模拟”［24，25］。在ANSYS Fluent 中实现的SST-SAS 模型的传输方程其定义如下：

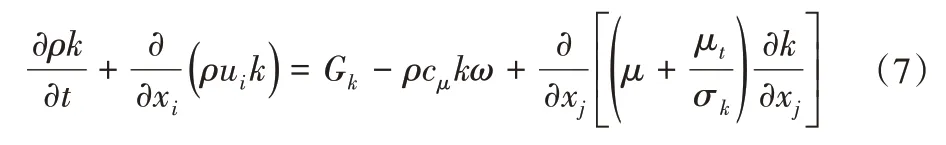
图2 不同的叶轮叶片Fig.2 Blade of different rotors

SST-SAS 模型方程（7）和方程（8）的输运方程与SST-RANS模型的不同之处在于，在湍流涡流频率的传输方程中，方程（8）中增加了SAS源项。

附加的源项QSAS为：

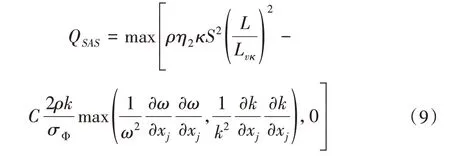
1.4 网格和时间步长无关性验证

整个计算域被分割成4 个区域，每个区域都采用结构化六面体网格。对墙附近的网格进行了优化，其中y+的平均值约为30。SIMPLEC求解器用于求解RANS方程组。以入口的质量流量和出口的总压力为边界条件，假定流动为不可压缩流动。在数值模拟中，网格的数目对计算的精度和效率有着重要的影响。通过调整网格密度，生成3 组网格，由此得到最佳效率点（Q*=0.77）的效率，如表1所示。当网格数超过8 439 405 时，结果几乎没有变化，因此在模拟中选择该网格，图3展示了局部网格的图像。测试了时间步长对瞬态计算的影响。使用了3个不同的时间步长，特别是0.000 119、0.000 238 和0.000 357 s，分别代表转子旋转周期的1/360、1/180和1/120。经过对比不同时间步长下的监测点数据，发现时间步长的差异可以忽略不计。考虑到流场细节和计算速度，所有后续数值模拟均选择时间步长0.000 238 s，数值模拟一共计算20 个旋转周期，总计算时间为0.856 8 s。采用最后10 个周期的数据进行平均，计算得到扬程和效率。

表1 网格敏感性验证Tab.1 Mesh sensitivity verification

图3 局部网格Fig.3 Local view for the mesh

1.5 模拟精度验证

实验结果［23］与数值模拟得到的计算结果如图4所示，其中实验的最佳效率点是Q*=0.76，数值模拟的最佳效率点是Q*=0.77。对比结果表明，模拟结果在变化趋势和具体数值上都是准确的，验证了数值模拟方法的可靠性。

图4 轴流式喷水推进泵性能曲线Fig.4 Performance curves of the axial flow waterjet pump

2 结果和讨论

对不同波状前缘叶轮的喷水推进泵进行了数值模拟计算，得到了在各工况下性能数据，并与原型喷水推进泵进行对比。如图5和图6所示，应用波状前缘之后，当流量低于最佳效率点流量时，喷水推进泵的扬程、效率有所降低。当流量超过最佳效率点流量时，喷水推进泵的扬程、效率有所升高。且流量较大时，喷水推进泵的性能提升更明显。尤其配置参数为4/s0.12C的波状前缘叶轮，在大流量Q*= 1 时，扬程、效率提升最大。

图5 不同波状前缘叶轮喷水推进泵扬程变化图Fig.5 Head variation of the waterjet pump for different rotors with leading-edge tubercles

图6 不同波状前缘叶轮喷水推进泵效率变化图Fig.6 Efficiency variation of the waterjet pump for different rotors with leading-edge tubercles

为了进一步研究波状影响的原因，本文采用了熵产分析［26］，可以对喷水推进泵内部能量损失情况进行更详细地研究。如图7和图8所示，分别是在Q*= 1 时，原型喷水推进泵［图（a）、（b）、（c）］和配置参数为4/s0.12C的波状前缘叶轮喷水推进泵［图（d）、（e）、（f）］叶轮和导叶不同叶高处归一化熵产分布图。在大流量下，原型喷水推进泵叶轮和导叶区域有大范围的熵产分布，意味着此时原型喷水推进泵内部有较大的能量损失。在叶轮和导叶区域，其熵产都主要集中在叶片的前缘和后缘，以及叶片之间的流道。而配置参数为4/s0.12C的波状前缘叶轮喷水推进泵叶轮和导叶区域熵产分布较少，内部能量损失相对于原型喷水推进泵有明显降低。在叶轮和导叶区域，只有少量的熵产分布在叶片的前缘和后缘，且流道中的熵产分布几乎消失。在Q*=1 时，波状前缘的应用，明显降低了喷水推进泵的能量损失，这直观地解释了大流量时波状前缘叶轮喷水推进泵效率提升的原因。

图7 叶轮中不同叶高处归一化熵产分布图Fig.7 Distribution of normalized entropy production at different relative spanwise heights in rotor

图8 导叶中不同叶高处归一化熵产分布图Fig.8 Distribution of normalized entropy production at different relative spanwise heights in stator

图9展示了原型喷水推进泵［图9（a）、（b）、（c）］和配置参数为4/s0.12C的波状前缘叶轮喷水推进泵［图9（d）、（e）、（f）］叶轮内部流场图。在Q*=1 时，原型喷水推进泵叶轮内部流线杂乱，流速分布不均匀，对应了之前的熵产分布结果。叶片之间的流道中有不稳定的流动，这是该处存在大量能量损失的根本原因。配置参数为4/s0.12C的波状前缘叶轮喷水推进泵内部流态良好，所以能量损失小。在大流量时，波状前缘抑制了叶轮内部的不稳定流动，这与在大攻角下波状前缘对翼型的作用类似［21］。图10展示了原型喷水推进泵［图10（a）、（b）、（c）］和配置参数为4/s0.12C的波状前缘叶轮喷水推进泵［图10（d）、（e）、（f）］导叶内部流场图。受上游叶轮内部流动的影响，原型喷水推进泵导叶区域流线混乱，流速分布不均匀，而应用波状前缘后，导叶区域流态明显得到改善，这也印证了之前的熵产分布结果。考虑到轴流式水力机械的共性，当前提出叶轮波状前缘设计方法同样适用于其他轴流式机械，特别是需要偏离设计工况点调节的情况，需要注意的是最优参数的组合会不同。

图9 叶轮中不同叶高处流场图Fig.9 Flow field at different relative spanwise heights in rotor

图10 导叶中不同叶高处流场图Fig.10 Flow field at different relative spanwise heights in stator

3 结 论

本文以轴流式喷水推进泵为研究对象，采用SST-SAS 湍流模型，研究了不同流量下波状前缘对轴流式水力机械水力性能的影响，主要的结论如下。

（1）相对于原型喷水推进泵，在小流量下，波状前缘叶轮喷水推进泵的能量损失增加，水力性能有所下降。在大流量下，波状前缘叶轮喷水推进泵的能量损失减少，水力性能有明显提升。

（2）大流量下波状前缘叶轮提升轴流式喷水推进泵性能的主要原因是波状前缘对流动的被动控制作用，能够抑制叶轮内部的不稳定流动，从而降低由此引起的能量损失。

（3）大流量下不同参数的波状前缘对轴流式喷水推进泵水力特性均有不同程度的改善，在当前参数的选择中，4/s和0.12C的组合最优。 □