基于ANSYS的新中式实木椅力学分析

俞明功，孙德林*，邹伟华，王张恒，姜夏旺，姚令华，孔竞

(1.中南林业科技大学材料科学与工程学院，长沙 410004；2.中山四海家具制造有限公司，广东 中山 528400)

新中式家具是基于我国传统家具美学、结合当代材料与加工技术、塑造具有我国传统文化特征且符合现代审美取向的一类家具[1]。新中式家具体现出简约、内敛的时代气息，继承传统红木家具的外观与架构或对传统中式家具框架进行简化[2]。在众多新中式家具系列产品中，实木家具系列产品占据重大比例且在人们日常生活中使用频率较高，所以实木家具在使用过程中容易发生结构破坏，对其进行结构强度受力分析有着重大的意义，如通过构件优化设计延长家具使用寿命、节约原材料以及提高家具的安全性等。目前对实木家具结构受力分析研究主要有两种方式：一种是对实木结构进行实验测试；另一种是使用数值方法进行计算分析处理，如有限元法(FEM)[3-4]。

有限元法在国内家具结构受力分析中主要应用于板式结构、框架结构，且集中于家具整体力学性能分析，如何风梅等[5]、宋明强等[6]、胡文刚等[7]研究有限元法在板式家具结构中的应用；张帆[8]、舒巍[9]运用有限元法分析实木椅类家具整体结构力学性能。但有限元法在椅类家具中的分析应用存在的问题主要有：选取分析的椅子模型偏于简单化且模型经过简化处理；其次是受力分析时，得到的是椅子整体云图，而不是椅子各部件受力云图，且并未根据椅子使用状况对椅子进行寿命预测估算。

针对有限元法在实木椅类家具的应用状况，以明式官帽椅为原型，基于新中式家具设计理念设计花梨木实木椅子，对其整体结构进行离散处理后，通过计算得到家具结构的整体性能及椅子各构件受力状况[10]，这既可以丰富明式家具体系研究，也能为新中式家具产品结构设计以及传统文物保护提供一定的指导。

1 模型建立

1.1 造型与结构设计

传统官帽椅零构件主要包括扶手、靠背板、角牙、联帮棍、鹅脖、牙条、前后腿、脚踏板、卷口牙子、横枨、罗锅枨、矮老等，如图1a所示。本研究以官帽椅为原型、以新中式家具设计理念为导向进行设计，椅子造型如图1b所示。新中式实木椅构件中运用的榫卯结构类型有挖烟袋锅榫、圆柱二位维丁结合榫、平板明榫角结合、圆棒榫、方榫等，去除了传统官帽椅的联帮棍，其基本尺寸图如1c、d所示。

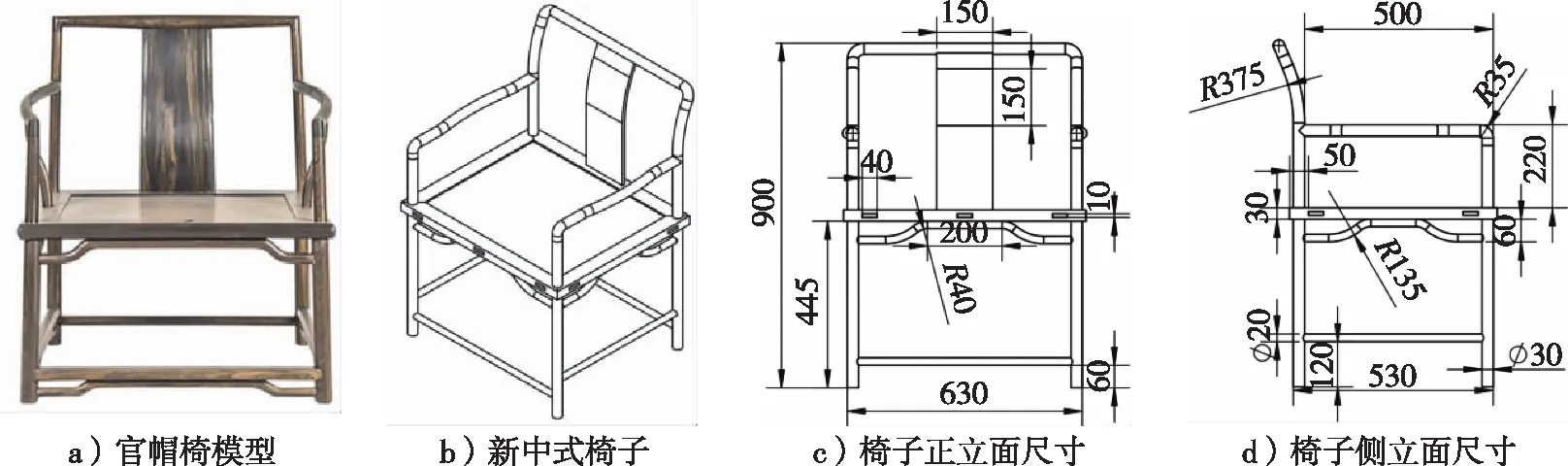
单位：mm图1 官帽椅及新中式椅子造型Fig. 1 The Official Hat Chair and new Chinese style chair

为了更真实模拟出新中式实木椅榫卯结构，将图1b中的椅子构件进行拆分，具体结构如图2所示，其中构件中圆棒榫的尺寸均为φ12 mm×40 mm。

单位：mm图2 新中式椅子结构细节图Fig. 2 Detail drawing of the structure of new Chinese style chair

1.2 模型建立

采用Soildworks软件建立新中式实木椅模型，如图3a所示，建成后将椅子的各个构件进行离散处理，有利于在受力分析时达到各部件受力的准确性[11-12]。该椅子共由27个构件组成，其拆开示意图如图3b所示，模型基本尺寸为630 mm×530 mm×900 mm。

图3 新中式椅子模型Fig. 3 The model of the new Chinese style chair

2 静力学分析

模型导入后，在软件中赋予实木椅花梨木材料基本属性，材料参数具体如表1所示，并在软件中查看椅子的质量约为14 kg。因为椅子自重也会对榫卯结构产生一定的影响，需要在后续分析中考虑椅子自重，这样可以使得椅子的受力分析更为准确。

表1 花梨木材料参数Table 1 Material parameters of Aniba rosaeodora

2.1 网格划分

优化网格设计对构件受力分析至关重要，网格划分的好坏会直接影响到构件受力分析的准确度以及构件的疲劳寿命分析预测[13-14]。由于设计的新中式实木椅子构件零件复杂且不规则，需要对模型分割处理后再导入分析，椅子分割图如图4a所示。采用六面体主导网格划分方法[15-16]，通过对不同的网格尺寸进行划分，检查划分后的网格质量(如网格单元质量、纵横比、翘曲因子、倾斜度及雅可比)来判断是否符合分析要求[14,17]，最后根据网格划分质量与求解计算结果精度来获得最精确的网格划分值，对椅子不同网格划分尺寸得到的数据如表2所示。

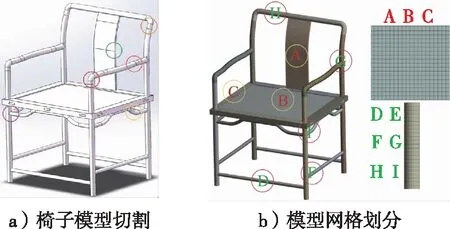
图4 新中式椅子网格划分图Fig. 4 The grid division diagram of new Chinese style chair

表2 不同尺寸网格划分数据Table 2 Meshing data of different sizes

从表2中数据分析可知：随着划分模型的网格尺寸值减小，模型得到的节点数与网格数快速增加，模型的网格质量在不断提高。在本分析中，当网格划分尺寸为5 mm时，椅子网格纵横比及翘曲因子值均已达到最佳，网格单元质量达到0.95，符合分析条件，故选取5 mm的网格划分尺寸作为椅子分析的前处理参数，得到椅子各部件网格划分图如图4b所示。

2.2 受力分析

在实木家具中，榫卯结构基本承受着构件的全部外载荷，造成椅子在受力时榫卯结构容易受到最大等效应力，进而发生结构破坏。同时，研究表明超重人数一直在不断地增加，而家具的功能和安全与使用者的体重有关，因此在设计与修正家具时，需要充分考虑使用者的体重[3]。另外，有限元模型分析结果在高载荷作用下的接触单元数目越多，结果越准确。因此，为了更能准确分析椅子的受力状况，参照GB/T 10357.3—2013《家具力学性能实验：第3部分 椅凳类强度和耐久性标准》第四等级座面静载荷试验水平标准，选定1 600 N载荷作为椅子座面施加的载荷，分析时并考虑椅子自重。椅子在竖直方向(Y轴)的受力按照公式(1)计算：

FY=F座+F椅

(1)

式中：FY为椅子在Y轴方向受到的总载荷，N；F座为椅子座面施加载荷，N；F椅为椅子自重，N。

代入数据得椅子在竖直方向受到的总力为1 740 N，考虑椅子各构件之间的摩擦，接触单元采用增广拉格朗日算法来加强表面间的接触和限制穿透[18]，这样会使椅子各部件之间的受力更为准确。基于以上边界条件，求解出椅子在受力状况下的等效应力云图、等效应变云图及总变形云图，如图5所示。

图5 实木椅应力、应变与变形云图Fig. 5 Cloud maps of stress, strain and deformation of new Chinese style chair

从图5中新中式椅子静力学分析的云图可知，花梨木实木椅子座面在承受1 600 N载荷时，椅子受到的最大等效应力值为7.62 MPa，如图5a所示，主要分布椅子腿部罗锅枨榫口下端位置；同时，椅子受到的最大等效应变为4.025×10-5，同样也分布在椅子腿部罗锅枨榫口下端处，如图5b所示；椅子受力时发生的最大变形为0.033 mm，最大变形主要分布在椅子座面中部，如图5c所示。

2.3 安全验证

为验证椅子受力时各结构是否处于安全状态，需要考虑木材的结构强度——木材的容许应力，木材的结构强度是指木材抵御外界所施加应力后而不发生破坏的能力。应用ANSYS分析家具结构受力时引入木材容许应力的意义有：一方面是确保家具的结构使用安全性；另一方面是最小限度地消耗原材料，合理使用木材，降低生产成本。木材容许应力按照公式(2)计算：

[σ]=σ12·K

(2)

式中：[σ]为含水率为12%条件下木材容许应力值，MPa；σ12为含水率为12%条件下木材强度的平均值，MPa；K为木材折减系数，一般取木材的折减系数为顺纹抗压强度取0.245，抗弯强度取0.148，抗剪强度取0.201。

从图5a中可知，椅子在承受载荷时，椅子腿部受到的等效应力最大，主要表现为木材强度中的抗弯强度。参照常用木材物理力学性质中第6种木材等级(密度为0.963 g/cm3，顺纹抗压强度为71.4 MPa，抗弯强度为152 MPa，抗弯弹性模量为17.3 GPa)进行椅子安全验证对比[19]，椅子的安全因子使用公式(3)计算：

[σ]=σ/n

(3)

式中：σ为材料断裂时的极限强度，MPa；n为材料构件的安全因子。

第6种木材等级抗弯容许应力值为22.496 MPa，将椅子受力时的应力7.62 MPa代入(3)式中得到椅子的最小安全因子为2.95，但花梨木的密度、弹性模量均大于第6等级树种，所以花梨木制作的新中式实木椅构件的最小安全因子大于2.95，椅子在加载过程中不会发生结构破坏。

此外，椅子使用寿命除了与椅子受力状况、使用环境、材料用材、制作工艺等有关之外，还与使用循环次数有关。椅子在日常生活中使用频率较高，因承受不同体重的人，椅子受到的应力、应变与变形及使用寿命也会有很大差别。为了能够更好地探究椅子的使用寿命，对其进行疲劳分析，确定构件在疲劳载荷下的损伤演化[20]，从而验证设计的可行性。

3 疲劳性能分析

在实木家具结构中，木构件之间常采用榫卯连接，当家具受力时，榫卯在抵抗外界载荷中起到至关重要作用，因此在榫卯连接处在受力时存在着失效形式，如木材榫卯连接处松动、榫被拔出、卯因受力而发生变形破坏等，这些损伤现象将显著影响弯曲能力、刚度、结构的完整性和安全性[21-22]。其中，榫卯结构破坏是木结构破坏的一个典型损伤类型，通过疲劳分析可以为探究椅子中榫卯结构破坏及损伤情况提供指导数据支持，从而为榫卯结构提供优化设计方案。同时，在椅子构件中，榫卯接触位置处存在应力集中问题，如图5a所示，其可能导致材料在承受循环荷载时局部屈服，同时也可能出现疲劳破坏[23-25]。

3.1 疲劳寿命计算

3.1.1 疲劳修正模型

有限元法的疲劳分析程序计算结果可以准确地预测构件损伤。因实木椅模型属于对称模型，在模拟实木椅疲劳分析时采用完全对称法，并选取Goodman理论作为实木椅的平均疲劳应力修正理论。对于给定的疲劳循环次数，Goodman理论可以准确预测分析实体的疲劳寿命曲线，即随着构件的平均应力增加，应力幅值达到极限后将会下降，从而使计算结果更为准确。Goodman的直线模型方程式为：

Sa=S(R=-1)[1-Sm/Sb]

(4)

式中：Sa为循环应力幅值，MPa；S(R=-1)为应力比等于1时的疲劳幅值，MPa；Sm为平均应力大小，MPa；Sb为极限强度，MPa。

3.1.2 疲劳损伤累积计算

构件的疲劳损伤累积计算应用较多的理论是Miner线性疲劳累积损伤理论。在多数情况下，运用Mine理论后材料结构疲劳寿命的计算结果与试验结果有相当程度的吻合，具有很好的可验证性和可行性，在工程上得到了广泛应用[26-27]。Miner线性累积理论的损伤度评估公式为：

(5)

式中：D为材料累积损伤指标；ni为实际应力循环次数；N为材料达到应力幅值下的循环寿命次数。

3.2 疲劳寿命分析

不考虑外在因素的影响(如空气含水率、不同地区的地域性等)，参照GB/T 10357.3—2013中椅子座面耐久性试验标准，对椅子座面施加950 N载荷后得到椅子的等效应力云图、等效应变云图、总变形云图如图6a、b、c所示。从图6中的云图可知：花梨木椅子受力之后，椅子受到的最大等效应力值为5.6 MPa，分布在椅子腿部罗锅枨榫口处，如图6a所示；同时，椅子受到的最大等效应变为3×10-5，同样也分布在椅子腿部罗锅枨榫口处，如图6b所示；椅子受力时发生的最大变形为0.024 mm，主要分布在椅子座面中部，如图6c所示。

图6 新中式椅子应力、应变与变形云图Fig. 6 Cloud maps of stress, strain and deformation of new Chinese style chair

基于椅子座面耐久性受力模拟得到的等效应力、等效应变及总体变形数据，在软件的疲劳分析模块中设置好椅子的循环使用次数为105次的边界条件，对椅子进行疲劳分析模拟，得到椅子的疲劳寿命云图、疲劳损伤云图如图7a、b所示。

图7 新中式椅子疲劳分析云图Fig. 7 Cloud chart of fatigue analysis of new Chinese style chair

从图7中椅子的疲劳寿命云图可知：椅子座面在承受950 N载荷循环加压时，椅子疲劳寿命最短的部位主要是罗锅枨榫口位置，如图7a所示，最小位置处可使用次数为1.078 8×108次。其次，在图7b椅子疲劳损伤云图中，椅子疲劳损伤最大的位置也发生罗锅枨榫口位置，疲劳损伤值最大值为0.26(小于1)，椅子在循环加载过程中不会发生结构破坏。基于以上分析条件设置，求解得到椅子的疲劳寿命曲线图，如图8所示。从图8中可知：在0～6 MPa内，花梨木椅的使用寿命随着受到应力的增加而逐渐减少，二者呈现非线性关系；椅子在加载条件下，使用次数最小值和最大值与疲劳寿命分析云图(图7a)一致，说明分析具有可行性。

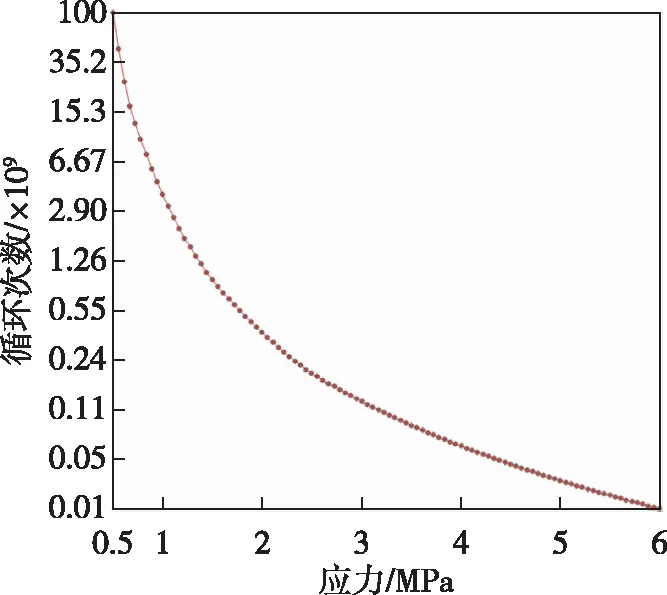
图8 新中式椅子疲劳寿命曲线图Fig. 8 Fatigue life curve of new Chinese style chair

4 结 论

基于新中式家具理念，以传统的官帽椅为原型，使用Solidworks建立新中式花梨木实木椅模型，利用有限元法分析新中式实木椅座面在承受1 600 N载荷时，椅子受到的应力、变形，判断椅子结构的安全性。同时，根据椅子耐久性实验标准对椅子座面施加950 N载荷进行加载循环，通过椅子循环加载得到的损伤值及疲劳寿命值验证新中式实木椅子设计可行性。为保证椅子受力分析的准确度，在软件中将椅子分成27个构件，得到的结论如下：

1)椅子座面受到1 600 N载荷加载时，椅子受到的最大等效应力值与应变值分布在椅子腿部罗锅枨榫口处，分别为7.62 MPa、4.025×10-5；椅子发生的最大变形为0.033 mm，主要分布在椅子座面中部处。

2)参照第6等级木材物理力学性质对椅子结构进行安全性判断，得到椅子座面受到1 600 N载荷加载时，椅子构件最小安全因子发生在腿部罗锅枨榫口处，此处的最小安全因子大于2.95，椅子在加载过程中不会发生结构破坏。

3)当椅子座面受到950 N载荷循环加载时，椅子座面产生的最大变形为0.024 mm，椅子构件的最大等效应力值、最大等效应变值、疲劳寿命最小值、疲劳损伤最大值的位置是椅子腿部罗锅枨榫口处，此处的最大等效应力值为5.6 MPa、最大等效应变值为3×10-5、疲劳寿命最小值为1.078 8×108次、疲劳损伤最大值为0.26，且椅子的疲劳寿命曲线与椅子疲劳寿命云图数据一致，椅子在循环加载过程中不会发生结构破坏。