圆台型螺旋能量桩换热性能的数值模拟研究
甘飞 黄光勤 张洪宇 庄春龙 成镭 许宁格
陆军勤务学院军事设施系
0 引言
能量桩[1]是一种依托于建筑基础而设置的桩基地埋管换热器,也是地源热泵与土壤源实现热量交换的关键部件,其换热特性直接影响热泵机组的效率及运行。能量桩可分为U 型和螺旋型[2-6],相较U 型能量桩,螺旋型能量桩具有几何结构复杂、桩径大、埋深浅、单位深度换热量大、换热效率高[7]等特点,单纯地以U 型 能量桩模型已不能准确反映其传热机理及特性。为此,关于螺旋型能量桩的研究应运而生。
本文将以具有高传热性能的圆台型螺旋能量桩为研究对象,通过机理简化,采用环形管等效热源数值模拟模型,进一步分析不同锥角的圆台型螺旋能量桩在相同螺距时的内部传热特性。
1 圆台型螺旋能量桩数值解模型
1.1 圆台型螺旋能量桩结构
圆台型螺旋能量桩的几何结构呈圆台型,其布置如图1 所示。螺旋换热管缠绕在由钢筋制成的圆台面上,圆台的锥角为θ,相邻螺旋管间的距离d保持相等,螺旋管的螺旋半径r沿深度z 方向线性递减。整个圆台型螺旋能量桩埋于地下,螺旋换热管顶部半径为rt,底部半径为rb,其中rt > rb。螺旋换热管顶部离地面距离为ht,底部距离地面距离为hb。相邻螺旋管间的距离d与深度方向z上螺距b的关系为b=d·c os(θ)。

图1 圆台型螺旋能量桩
1.2 圆台型螺旋能量桩数值解模型
圆台型螺旋能量桩运行时,流体从螺旋换热管内顶部进入,沿换热管螺旋流动,同时与回填区域进行热交换,最后由螺旋换热管底部流出进入热泵机组下一部件。文献[8]提出的环形管等效热源数值建模方法已得到实验验证,具有计算速度快、准确度高、可较为真实反映能量桩传热规律的特点,故本文将采用环形管等效热源数值建模方法对圆台型能量桩进行数值模拟。
建模思路如下:将连续的螺旋换热管简化为对应螺旋圈数量的环形管,如图 2(a)所示。假设管外回填料及岩土各向同性,因此在相同深度和半径,回填料及岩土的热物性参数相同,进而可将三维环形管模型简化为二维轴对称模型,如图 2(b)所示。

图2 螺旋管简化示意图
环形管等效热源的热量传递如图3 所示,具体计算如下:

式中:qi为第i圈环形管等效热源向周围区域释放的热量,W;qm为管内流体质量流量,kg/s;cp为管内流体比热容,J/(kg·℃);Ti为第i圈环形管等效热源温度,Ti-1为第i-1 圈环形管等效热源温度,℃。
环形管等效热源外传热方式为固体导热,因此在图2(b)柱坐标系下建立第i圈环形管等效热源外导热微分方程为:
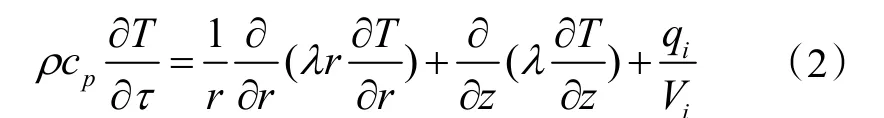
式中:ρ为导热介质的密度,k g/m3;cp为导热介质的比热容,J/ (kg·℃);λ为导热介质的导热系数,W/(m·℃);T为导热介质对应坐标r,z下的温度,℃ ;qi为第i圈环形管等效热源向周围区域释放的热量,W ;Vi为第i圈环形管等效热源体积,m3。

图3 等效热源示意图
2 结果与分析
2.1 仿真平台及参数设置
本文采用商用 CFD 软件 COMSOL Multiphysics 进行数值模拟计算。为便于计算,本文选取环形管模型垂直对称截面的一半作为研究对象,计算区域如图 4 所示,其中矩形计算区域的上边界为地面,左边界为垂直对称截面的对称轴,右边界与下边界为计算区域岩土边界。通过软件平台,分别建立了0°(圆柱)锥角,5°锥角,10°锥角,15°锥角和 20°锥角的圆台型螺旋能量桩模型,其物性参数和运行参数设置如表1 所示,几何结构参数如表2 所示。模拟计算时,保持进口水温恒定为35 ℃,环境温度为 20 ℃,模拟时长为 30000 分钟,约20.8 天。

图4 计算区域示意图
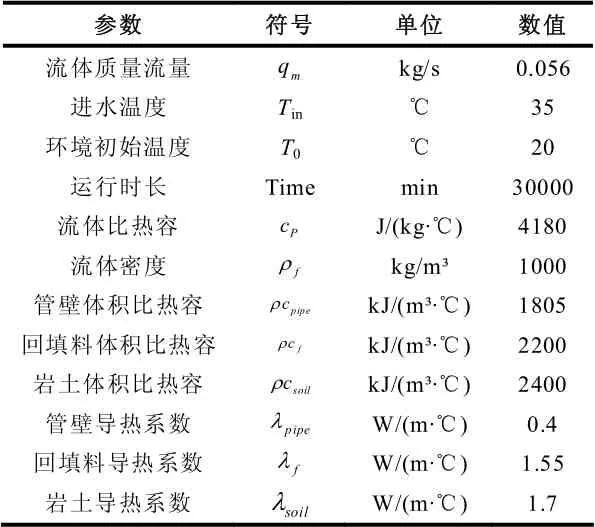
表1 模型物性参数及运行参数
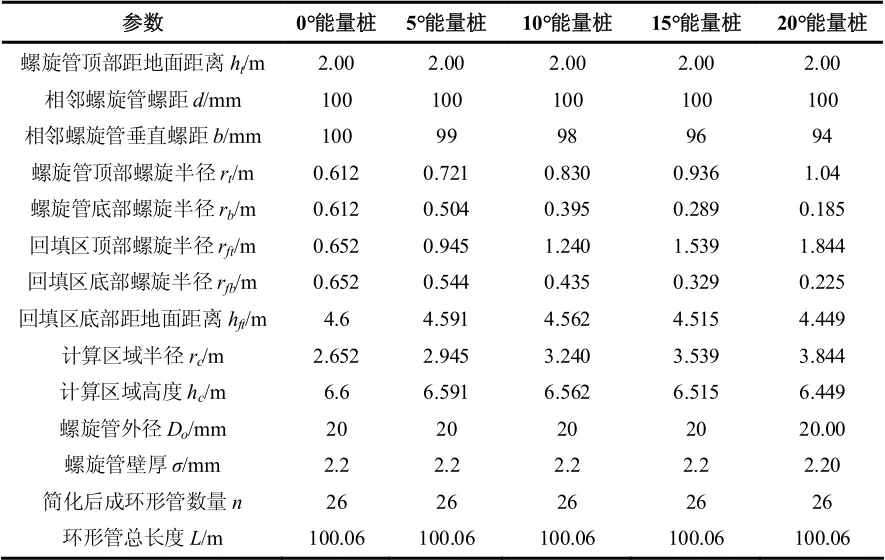
表2 螺旋能量桩几何结构尺寸
圆台型螺旋能量桩的网格划分示意图如图 5 所示,经网格无关性检验,上述5 种圆台型螺旋能量桩的网格数分别为 34727(0° 锥角),33160(5° 锥角),32428(10° 锥角),30984(15° 锥角)和 30648(20° 锥角),且均已达到网格无关性要求。

图5 网格划分示意图
2.2 能量桩整体换热能力分析
为了分析能量桩的整体换热能力,本文从螺旋管换热器的单位面积换热量qw来衡量,定义如下。

式中:Q为螺旋管放热量,W;S为能量桩的侧面积,m2;l为圆台能量桩的母线长度,m;rt和rb分别为螺旋管顶部螺旋半径和底部螺旋半径,m。
文献[8-9]分析了不同锥角圆台螺旋型能量桩在相同垂直螺距(能量桩高度及埋深相同)条件的换热能力,其中,圆台型能量桩锥角越大,相邻螺旋管之间的绝对距离则越大,相互之间的热干扰强度则越小,其整体换热效果越好。文中建立的5 种不同锥角的圆台螺旋能量桩,将螺旋管的螺距设置为 100 mm,既保证了不同锥角能量桩的相邻螺旋管之间的距离相等,同时也保证了能量桩的侧面积相等,从空间结构上消除了相邻螺旋管间热干扰的差异对研究能量桩换热能力的影响。
通过数值模拟计算,得到不同锥角圆台型螺旋能量桩的单位面积换热量随时间的变化,如图 6 所示。随着能量桩的运行,各螺旋能量桩的单位面积换热量均呈指数下降趋势变化,初期阶段急剧下降,随后进入过渡阶段,最后进入准稳态。各圆台型螺旋能量桩的单位面积换热量相差不大,为了更加清晰观察各能量桩之间的换热量差异,以 0° 圆台螺旋能量桩为基准,计算出其余能量桩的单位面积换热量增长率,计算公式如式(5)所示。分别取初始阶段,过渡阶段及准稳态阶段的部分时刻,得到圆台型螺旋能量桩的单位面积换 热量增长率,如表3 所示。
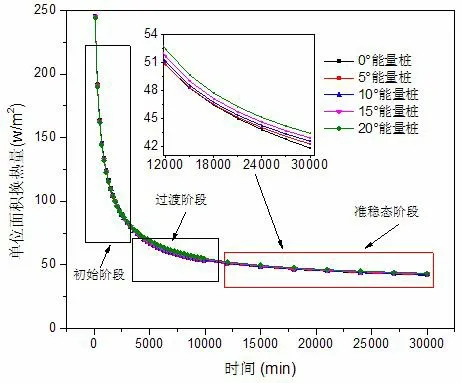
图6 能量桩的单位面积换热量随时间变化
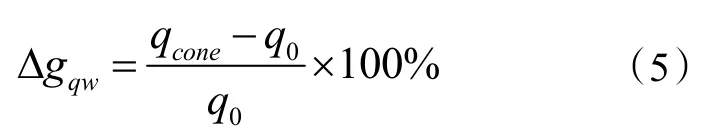
式中:qcone为圆台型螺旋能量桩单位面积换热量,W/m;q0为圆柱型螺旋能量桩单位面积换热量,W/m。

表3 圆台型螺旋能量桩的单位面积换热量增长率
从表 3 可知,圆台型螺旋能量桩单位面积换热量增长率是随着传热过程动态变化,先下降后上升。在传热初期,随着锥角的增大,单位面积换热量增长率呈下降趋势,即圆台锥角越大,单位面积换热量越小,说明小锥角的圆台螺旋管换热效果更好。随着热传导的进行,尤其是进入传热过渡阶段之后,单位面积换热量增长率已呈上升趋势,即圆台锥角越大,单位面积换热量越大。因此,本文所建立的能量桩模型消除了螺旋管之间空间距离的不同对传热的影响,从整体结构上进一步验证了在传热后期大锥角圆台型螺旋能量桩具有更好的换热能力。
2.3 能量桩内部换热能力分析
从以上分析可知,5 种圆台型螺旋能量桩除沿深度方向的螺旋管螺旋半径不同外,其余物性参数、运行条件、几何结构均一致,所呈现的整体换热能力各不相同,可见能量桩沿深度方向的螺旋半径对其换热能力有明显影响。由于本文的建模思路是将连续的螺旋型换热管简化为对应螺旋圈数的环形管等效热源,因此某一圈环形管的单位管长换热量可代表在该深度、螺旋半径条件下螺旋管换热器的换热能力,单位管长换热量ql定义为式(6):

式中:Q为螺旋管放热量,W;L为螺旋管长度,m。
图7 为各圈环形管所在位置,共26 圈。通过计算,得到终止时刻(30000 min)圆台型螺旋能量桩由上至下每一圈的换热量。如图8 所示,沿深度方向,在能量桩上部范围内(1-13 圈),20° 圆台能量桩换热量最大,0° 圆台能量桩换热量最小。而在能量桩下部范围(14-26 圈),则呈现相反趋势。这是由于圆台能量桩锥角的存在,导致大锥角的圆台能量桩的上部分螺旋管长度更长,整体换热量则更多,下部分螺旋管长度短,整体换热量就更少。而圆台型能量桩各圈的换热能力却并非如总换热量一致变化,换热能力可从各圈的单位管长换热量体现,计算结果如表4 所示。
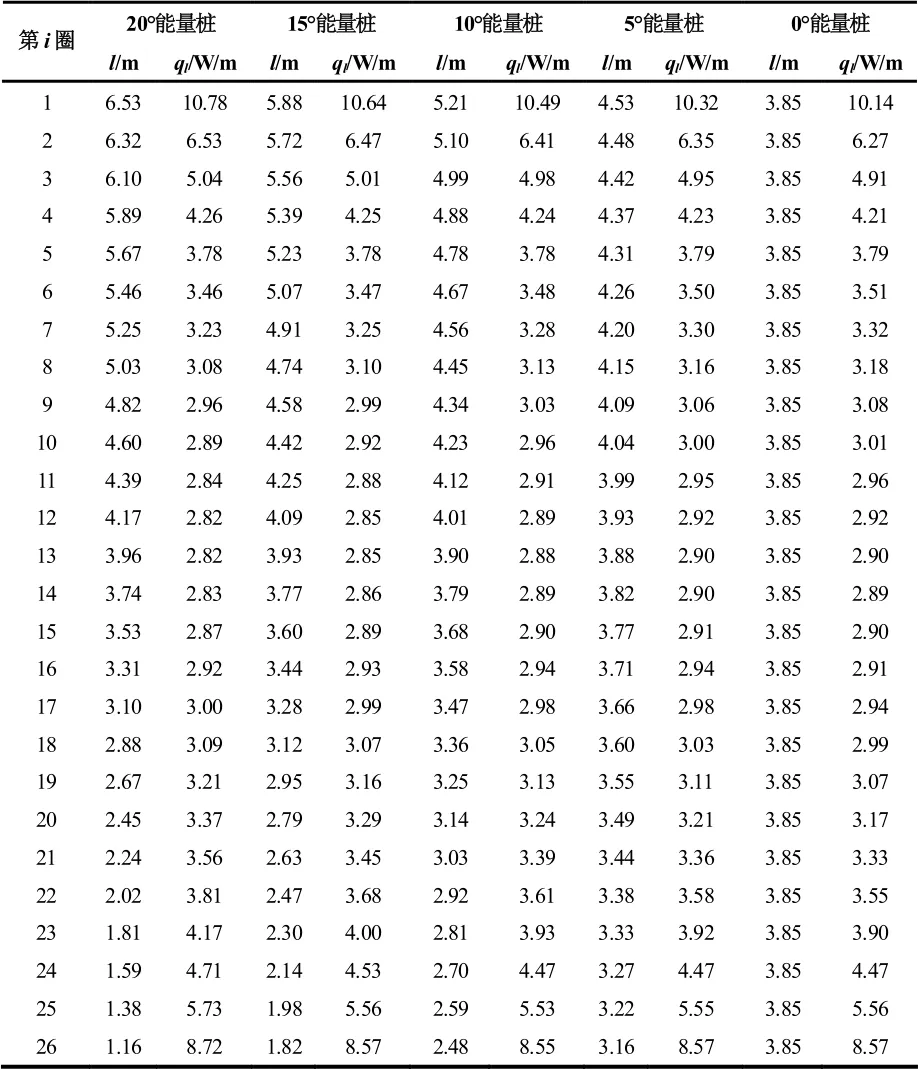
表4 圆台型能量桩内部换热能力

图7 环形管位置示意图

图8 圆台型能量桩内部螺旋管换热能力对比
由表 4 可知,对于同一能量桩,圆台型螺旋能量桩的单位管长换热量沿深度方向呈U 型分布,即螺旋管上层入口管段和下层出口管段部分的单位管长换热量大,中间管段部分的单位管长换热量小。以 0° 锥角能量桩的单位管长换热量为基准,沿深度方向将能量桩的螺旋管分为上层入口管段(第 1~4 圈),中部管段(第 5~15 圈)和下层管段(第 16~26 圈)。在上层入口管段的管圈,能量桩的锥角越大,其单位管长换热量更大,换热能力更强。在中部管段的管圈,能量桩的锥角越大,其单位管长换热量却更少,换热能力更弱,尤其在第 8~11 圈,20° 圆台型能量桩同比其余能量桩的换热能力减到最弱。在下层管段的管圈,能量桩换热能力随圆台锥角增大而增大,在第21~23 圈,20° 圆台型能量桩换热能力同比其余能量桩增至最强。以上为各能量桩的螺旋管圈换热能力对比,从其内部结构的换热能力可知,并非大锥角能量桩的任意管段换热能力均比小锥角能量强,若要使能量桩具有更好的换热能力,则需尽可能地增大换热能力强的管段占比。表5 为各能量桩在上、中、下层的管段占比及换热量占比。定义换热强度因数σ,如式(7)所示。

式中:γl表示该段螺旋管的长度占全长比例,%,γQ表示该段螺旋管换热量占总换热量比例,% 。
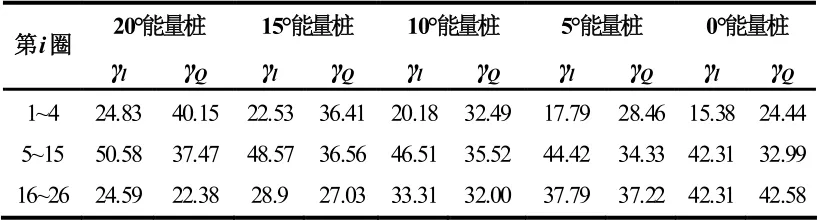
表5 各能量桩换热管段及对应管段换热量占比
表6 为各能量桩在不同管段的换热强度因数,由表 5 和表 6 可知,在上层入口管段,20° 能量桩用 4.83%的管长进行了40.15%的热量交换,而0° 能量桩用15.38%的管长进行了24.44%的热量交换,其强度因数分别为 1.62 和 1.59。在下层管段,20 ° 能量桩用 24.59%的管长进行了22.38%的热量交换,而 0° 能量桩用42.31%的管长进行了 42.58%的热量交换,其强度因数分别为0.91 和1.01,说明在上层大锥角的圆台能量桩局部换热能力更强,而中、下层部分小锥角能量桩的局部换热能力更强。由于大锥角能量桩在上部分换热能力突出,其管段占比较大,因此综合下来大锥角能量桩的整体换热能力更强。可见,如果要提高螺旋能量桩换热能力,可将能量桩的上层螺旋管段呈较大圆台锥角布置,中下层螺旋管段呈小锥角圆台或圆柱型布置。

表6 各能量桩换热强度因数
3 结论
本文以圆台型螺旋能量桩为研究对象,结合其几何特征与传热机理,采用环形管等效热源数值建模方法,对螺旋能量桩传热特性进行分析。主要结论如下:
1)在传热过渡期后,圆台型螺旋能量桩的单位面积换热量随圆台锥角的升高而增大,大锥角圆台螺旋能量桩换热效果更好,其中在传热终期,20° 圆台型螺旋能量桩比 0° 圆台能量桩的单位面积换热量提高了 3.81%。因此在工程实际中,大锥角的圆台螺旋能量桩具有更强的换热能力。
2)通过对圆柱,5° 锥角,10° 锥角,15° 锥角和20° 锥角圆台型螺旋能量桩的内部单位管长换热量计算,并引入换热强度因数的概念,发现在圆台能量桩上层管段部分,单位管长换热量随圆台锥角的增大而增大,而能量桩中部及下层管段的单位管长换热量随圆台锥角的增大而减小,可见对于圆台螺旋能量桩,适当优化中间及下层部分的空间结构,可进一步提高能量桩换热能力。

