基于模糊系统的飞行冲突探测与解脱

冯思嘉，季玉龙

（1.四川大学视觉合成图形图像技术国防重点学科实验室，成都610065；2.四川大学空天科学与工程学院，成都610065）

0 引言

随着民航企业的发展，飞行流量的增加，有限的空域资源逐渐不能满足增加的交通流量，导致两者之间的矛盾变得日益突出，因此对飞行安全、效率、空管服务品质有了更高的要求[1]。这样的问题在进近区域体现更加显著[2]。智能化的冲突管理能够对潜在冲突进行探测，若发现有冲突则对飞机航向进行微调，能有效的使飞机汇聚在一起时并保持一定的安全间隔，这样智能化的冲突管理能为管制员提供辅助决策，减轻他们负担的同时提高进近空域资源的利用率，为完善航空管理体制与运行机制做贡献。

飞机智能化冲突管理核心主要包括两部分：冲突探测与冲突解脱[3]。冲突探测是对飞机的轨迹进行预测，然后判断航空器是否小于间隔标准，如果有小于则判定为存在潜在冲突，发出冲突警告。对于存在潜在冲突的飞机进行冲突解脱，即为它尽快重新规划一条以飞机耗能少为原则的无冲突路径。飞机在空中情况是瞬息万变的，很多因素都会影响到路径规划，同时又伴随着许多不确定性和随机性，使得系统输入参数过多，过于复杂。

模糊控制能够有效解决上述难题，模糊控制具有稳定性高、适应性强，计算效率高等优点，能高效处理输入较多的情况[4]。传统的模糊系统使用专家知识将模糊逻辑用于智能控制，Hagras 提出了FLS[5]，这种模糊逻辑可以提高在不确定条件下模糊系统的性能，以便在动态变换的环境中实现智能控制。Mobadersanyetal[6]，提出了一种基于模糊逻辑的实时方法来解决由未知移动障碍引起的路径规划问题。FLS 具有固有鲁棒性，非常适用于现实生活中的应用。FLS 也已经针对PID控制器进行了调整[7-8]，而调整之后PID 不再使用恒定比例积分和微分，这些值会根据当前误差不断更新。然而随着输入输出的增加，手动调整FLS 的隶属函数和规则库的参数变得越来越困难。Jang 提出了一种ANFSIS[9]体系结构，该过程用反向传播算法对模糊系统的隶属函数和规则库进行调整。Shimojima[10]提出了一种基于GA 的监督学习机制。Jain[11]提出了一种使用模拟退火的优化过程。人工神经网络（ANN）也被用于开发控制器。通过强化学习对控制对象进行训练，以便在每个瞬间采用最佳行动以达到最终的期望状态。Q-learning 作为强化学习的一种，在神经网络中应用广泛，其中包括了Atari 游戏[12]，以及AlphaGo[13]系统等。Sathyan 等人分别使用强化学习和模糊系统对机器人进行训练，对比之下发现由于模糊系统的固有鲁棒性以及擅长对非线性系统的处理，使得模糊系统训练出的机器人任务成功率更高。

因此本文使用模糊系统来解决飞机冲突问题，将每一个飞机建立称为模糊子系统，利用当前飞机的相对位置判断飞机是否在其他飞机的保护半径之内，如果在，则获取当前两架飞机的相对接近速度和航向，通过这两个参数判定是否存在潜在冲突，如果不存在则不对其进行改变，让飞机保持原有的航向和速度进行飞行，如果存在则将相对位置、相对速度、相对航向作为模糊系统的输入，输出飞机的新航向，对飞机的轨迹进行修正，使得飞机在保证分离的情况下飞行路径最短，节省能耗。

本文第二部分对冲突探测和冲突解脱的逻辑模型进行解释说明，第三部分是对该系统的具体描述，第四部分是实验的建立与实验结果说明，最后第五部分是总结。

1 碰撞情景与系统框架建立

本文中，我们需要为进近范围内存在潜在冲突的飞机规划出一条无冲突路径，测试范围是一个以100km 为半径的圆形区域。如果被判定为存在潜在冲突，则需要依据优先级对飞机路径进行重新规划，重新规划的原则是：

（1）被改变的飞机数目尽量少；

（2）遵循设定好的优先级；

除上述的原则以外，结合飞机实际的飞行情况，进行实验的飞机速度介于150m/s～220m/s 之间，模糊系统对飞机航向的改变角度不超过30°。

圆形内部即为进近区域，飞机在进近范围外时，冲突保护距离为5nmi，当进入进近范围内之后，考虑到飞机数目虽然增加，因此冲突保护距离缩小为2.5nmi。进入进近范围的飞机，其所有基础航向都是朝向机场降落位置，每隔0.3 秒进行一次更新，并且计算出两两之间的相对距离，判定是否在对方的保护半径之内，如果在则获取两架飞机的相对航向，如果两架飞机是相向而行则使用模糊系统对优先级较低飞机的航向进行改变。以2 架飞机为例，其冲突模型的建立如图1 所示。A 与B 为两架进入测试范围的飞机，其航向分别为HA 与HB。

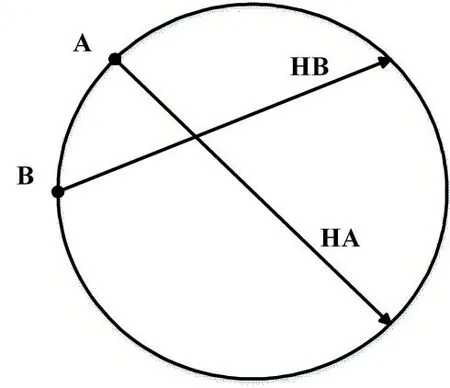
图1 冲突模型建立

图2 更改航向模型

如果不对飞机航向进行修正，飞机则会发生冲突，通过将每个飞机都建模成一个模糊子系统来解决此次冲突问题，每个模糊子系统对应着3 个输入和1 个输出，输入分别是相对航向、相对速度以及相对距离，输出是转弯率。图3 所示即为期望的被更改航向之后的模型图。

2 冲突探测与解脱

2.1 冲突探测

冲突探测是判定飞机之间的间隔是否小于间隔标准，传统的方法是判定到小于最小间隔标准之后则发出冲突预警[14]，并未对小于标准间隔的飞机对进行相对航向的判定，假设两架飞机虽小于安全间隔，但是航向相反，则不会发生冲突，这里将其称为假性冲突，如果对存在这种冲突的飞机对进行路径的重新规划，则会对资源进行浪费，因此论文除了会对冲突间隔进行建模，还会对相对航向进行判定。

（1）冲突间隔与保护区建立

最小安全间隔会随着轨迹的密度和空域区域而改变，一般而言，在一段航路空域中，两架飞机的水平最小安全间隔的公认值为5nmi，而在飞机降落和进场的进近扇区中该值会减少为2.5nmi。

飞机的保护模型主要分为以下三种：长方体保护模型、椭球形保护模型、圆柱体保护模型。由于保护区域的连接函数需要分开进行表示，且各个表面连接处不可导，导致后续计算较为复杂。因此为方便计算设计了椭球体模型和圆柱形模型。在论文中采用圆柱体模型如图3 所示。

图3 保护模型建立

以飞机为模型质点中心，高为2 倍危险接近的最大高度0.2nmi，以最小保护半径为半径s 建立圆柱体。任何进入建立保护区域的其他飞机被定义为小于冲突半径。飞机的圆柱体保护模型所建立的区域范围可以表示为：

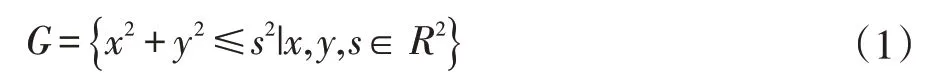
（2）相对位置与航向判定

在本文中需要对处于保护区内的存在潜在冲突的飞机进行航向的判断。假设已经检测到飞机A 在飞机B 的保护区域之内。

图4 相对位置判定示意图

获取到当前时刻飞机A 的航向为HA，飞机B 的航向为HB，相对航向：

由于直接比较HAB会有许多种情况且有不确定性，而在飞机的控制中最重要的就是实时性，如果为了追求过度的精准而拾取算法的实时性是不合理的，因此为了避免对相对航向进行分类讨论而增加复杂性，所以在一开始对飞机的相对位置进行计算，这种计算是合理的因为如果飞机有发生相撞的可能性，在调用模糊系统时也是需要对相对位置进行计算的。

所以在计算相对航向之前先进行相对位置的判定，假设飞机A 的横坐标为XA，飞机B 的横坐标为XB，判断的值XAB=XA-XB，如果XAB>0，则飞机A 在飞机B的相对右边，反之则为左边。考虑一种情况，当飞机A在飞机B 的相对左边时，如果飞机A 的航向属于[0,180]这个范围，且飞机B 的航向属于[180,360]这个范围时，就算两架飞机距离较近，也不会实际发生碰撞，但若不满足上述条件，则有发生碰撞的可能性，即需要通过模糊系统对航向进行修正。

2.2 基于模糊树的冲突解脱

本文采用模糊系统对具有潜在冲突的飞机进行航向调整。模糊控制是基于经验和知识的一种规则控制，在控制中可以对复杂的数学模型进行控制，具有控制机制容易实现过程简单的特点。相比于CNN 等深度学习算法[15]，模糊系统不需要其他辅助特征信息的输入，在该模糊系统中输入包含：相对航向、相对速度、接近率，对应的输出为对飞机航向。在获取输入之后需要对输入进行归一化处理。优先级较低的飞机的航向改变之后，考虑到飞机本身的限制，在对航迹进行计算的时候，应使新产生的点在其转弯半径上。同时由于模糊系统过程简单精度不高，这导致在飞机进入机场准备降落时，不能够精准地到达预期位置，所以在进近范围内时，采用模糊系统进行控制。

建立模糊系统有如下步骤：

①确定输入和输出变量，对输入变量进行归一化处理；

②确定输入变量和输出变量的隶属度函数；

③使用if-then 语言，建立模糊规则；

④得到相应的输出；

⑤去模糊化处理。

在本文中，模糊系统将两架可能发生冲突的飞行器的相对距离、相对航向以及接近率作为输入。即可能发生冲突的飞机A 与飞机B 对模糊系统的相对航向、相对距离、接近率可以分别用以下式子进行表示：

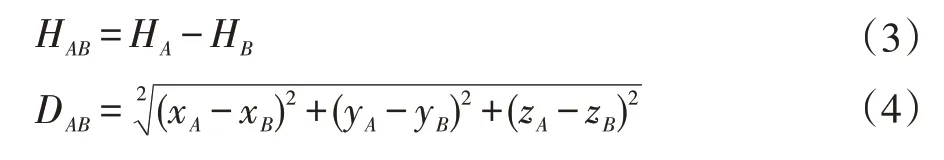
值得说明的是在这里计算的相对航向与上述的有所不同，这里用优先级更高的飞机作被减数，在这个例子中飞机A 拥有更高的优先级（飞机A 比飞机B 离降落点更近），其中DAB表示飞机A 与飞机B 之间的直线距离，VA和VB表示A 与B 两架飞机的速度。

川系火锅是我们最常见的火锅类型，我想，提起火锅一半人想到的是麻辣，另一半人想到的就是川渝。川系火锅一般认为分为四川火锅、重庆火锅、鱼头火锅以及串串香。

在对相对航向计算完后，判断其结果的正负：

如果Heading＜0，则Heading=HA-HB+360；

如果Heading＞0，则Heading=HA-HB。

在进行了上述判定之后，进一步对入和输出进行归一化的处理（以Heading＞0 为例）用以下式子进行处理：

其中R 表示保护半径（不同区域内飞机保护半径不同），Vmax表示飞机最大飞行速度。本文将飞机航向偏转度作为模糊系统的输出，由于前面的输入是进行过归一化的处理，因此通过模糊系统的输出也是一个归一化的值。考虑到飞机性能的限制，不可能做出过大的转弯幅度，所以经过模糊系统实际输出的值乘最大偏转度，才是实际的偏转角度。飞机的最大偏转角度用Tmax表示，模糊系统输出的归一化值用out 表示，因此实际的偏转角度用Turn 表示为：

在构建隶属度函数的时候采用三角隶属函数对其进行构建。三角隶属函数模糊化运算比较简单，且模糊化结果具有一定的鲁棒性。由于有三个输入，因此对应有三个小的模糊子系统，分别对它们进行隶属度函数建立。

对于相对航向而言，可以通过比较值的大小来判断两个飞机的相对位置，以飞机A 拥有更高优先级为例，如果归一化之后的值小于0.5，则可以判定飞行器B 在飞行器A 的左侧。如果是大于0.5 则飞行器B 在飞行器A 右侧，因此可以构建如图5 所示的隶属函数。

同理对相对距离和相对接近率建立如图6-图7 所示的隶属度函数。

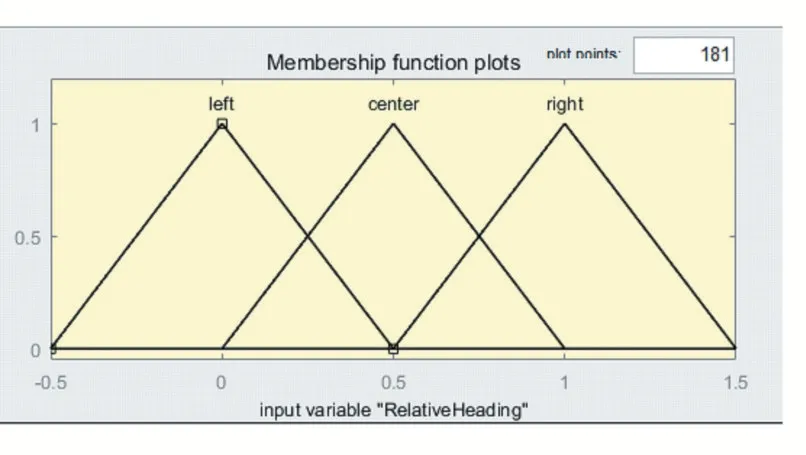
图5 相对航向隶属函数

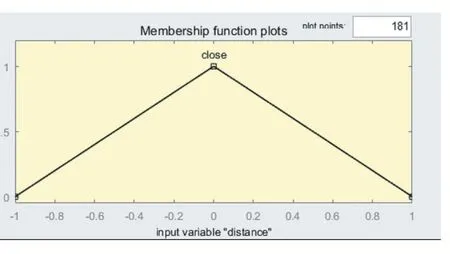
图6 相对距离隶属度函数

图7 相对接近率隶属度函数

在建立模糊规则之后，不同的三个输入变量经过模糊规则进行处理之后得到一个介于0 和1 之间的输出变量，然而这里的输出变量不能直接作为输出传给飞行器，因此还要经过去模糊化这一过程。将模糊的输出转换为精确的系统能操作的量。在本文中采用重心法。

3 实验建立与分析

3.1 总体构建

该程序运行的界面效在实验区域内，随机在不同位置生成10 架飞机，随机给予它们一个合理的初始速度和初始航向，飞行开始后，这10 架飞机每隔0.3 秒计算一次两两之间的间隔，这里需要说明的是每架飞机其实相当于时一个模糊子系统，当判定到保护半径内存在有危险的飞机时，使用模糊系统对存在冲突的飞机的飞行轨迹进行修改。例如在某次实验中，检测到飞机A 与飞机B 有冲突发生的可能性，且通过判定飞机A 的优先级高于B，则将飞机A 与B 的距离，A 与B的航向差，以及速度差，进行归一化处理之后，作为飞机B 模糊子系统的三个输入，通过设定的模糊规则，计算出飞B 的新航向。虽然可能出现，飞机B 改变航向飞行了一段时间后与飞机F 有了冲突，但是由于仿真系统每隔0.3 秒就进行一次距离计算，使得飞机有足够距离在相撞之前调整开距离。

3.2 实验验证

该以某次实验为例，随机生成飞机之后，从系统中得知A 飞机与B 飞机有冲突的可能性，立即产生冲突预警如图8 所示。

图8 冲突预警图

图9 为两飞机的飞行间隔距离随着仿真之间变化而变化的图，从图中可以看出仿真开始时，两飞机距离是13000m 左右，小于保护半径，经过模糊系统的调整之后，飞机在仿真38 秒左右到达距离最近9000m，之后两架飞机的距离则逐渐变大，直到80 秒左右，逐渐离开相互的保护半径，冲突警告关闭。

同时我们观察飞机B 的航向随时间变化的曲线图，如图10 所示，飞机B 的航向一开始是150 度，因为和飞机A 有冲突后，且优先级低于飞机A，因此对航向进行调整，从此图可看出，飞机的航向改变是缓慢的，不是一瞬间就完成的，在80 秒左右飞机航向保持不变，同时结合两家飞机的距离图，80 秒左右时，两飞机逐渐离开相互的保护半径。

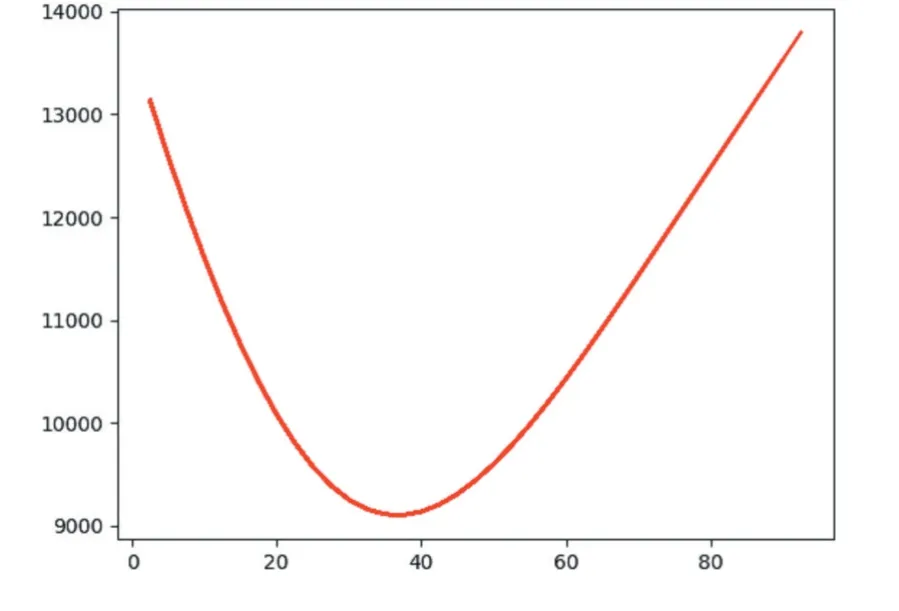
图9 保护半径变化曲线

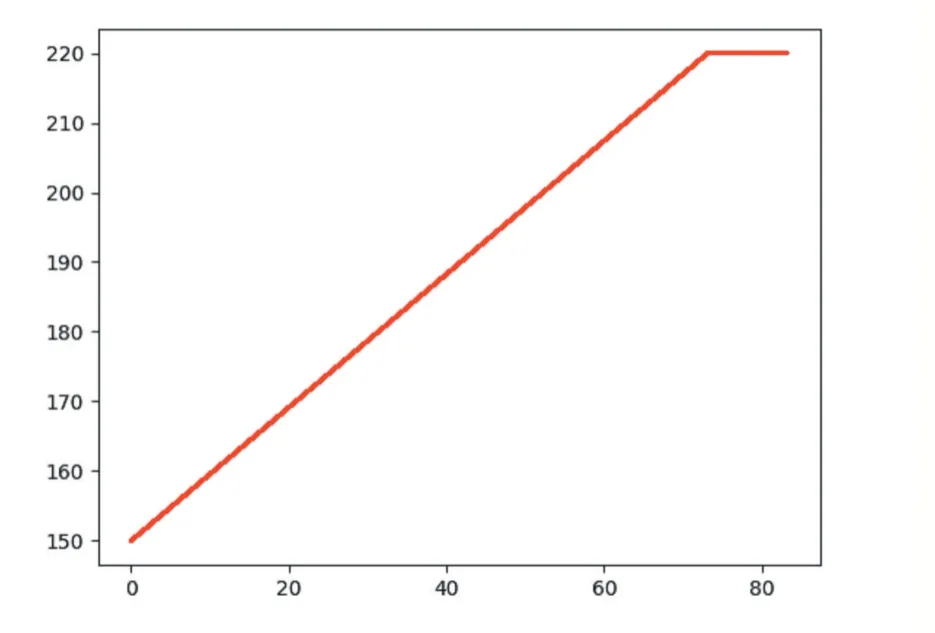
图10 改变后保护半径

总体上来看，一开始飞机A 与飞机B 相向而行，并且在相互的保护半径范围之内，从图11 中可以看出，飞机B 改变了航向，从而避免了碰撞的产生。

图11 飞行轨迹图

4 结语

在对飞机实行冲突管理时，由于存在许多外界不确定因素，使得系统的输入量较大，模糊系统具有鲁棒性、适应性强、高性能、计算效率高的特点，能有效解决上述难题，因此采用模糊控制对飞机飞行路径进行规划，通过上述实验可以看出，原本有冲突可能的两架飞机在通过模糊系统的运算之后，优先级较低的飞机通过改变航向的方式，避免了冲突的发生。