太原市COVID-19防控前后空气质量分析及预测

曹通 白艳萍

摘 要：为了探索特殊情况下太原市空气质量预测和评价方法，采用基于灰色关联度法的模糊综合评价方法对太原市疫情防控前后的空气质量进行评价，对相关联的污染物浓度变化进行分析，并以太原市AQI监测数据为基础，结合长短期记忆循环神经网络（LSTM）以及随机梯度下降算法（Adam）建立了太原市空气质量预测模型（即Adam-LSTM模型），并与LSTM模型的预测结果进行了比较。结果显示，在启动一级应急响应加强防控后，太原市的整体空气质量得到改善，个别污染物由于气象及春节等因素未降低，LSTM模型和Adam-LSTM模型预测结果的均方根误差和训练速度分别为0.203 s和12.15 s，0.183 s和10.35 s。提出的Adam优化算法能够有效提高LSTM神经网络的训练精度和收敛速度，同时具有较小的预测误差，可为环保部门制定提升空气质量相关决策提供数据支持和方法借鉴。

关键词：应用数学;灰色关联;模糊综合评价;Adam;LSTM;空气质量预测

中图分类号：O29;TP39;X823   文献标识码：A

DOI： 10.7535/hbgykj.2021yx02013

Air quality analysis and prediction before and after the prevention

and control of COVID-19 in Taiyuan

CAO Tong1，2， BAI Yanping1，2

（1.School of Science， North University of China， Taiyuan， Shanxi 030051， China;

2.Modern Optimization Algorithm Laboratory， North University of China，Taiyuan， Shanxi 030051， China ）

Abstract：

In order to explore the prediction and evaluation methods of air quality under special circumstances in Taiyuan， the air quality trend before and after the prevention and control of COVID-19 in Taiyuan was evaluated and the changes of related pollutant concentrations were analyzed by using the fuzzy comprehensive evaluation method based on grey correlation method. On the basis of the AQI monitoring data of Taiyuan， Long Short-Term Memory （LSTM） loop neural network and the stochastic gradient descent algorithm（Adam）， the Taiyuan air quality prediction model （Adam-LSTM model） was established， and the prediction results were compared with that of LSTM model. The results show that the air quality of Taiyuan is improved after the start of the first level emergency response， and some pollutants are not reduced due to meteorological and Spring Festival factors.The root mean square error and training speed of LSTM and Adam-LSTM model are 0.203 s and 12.15 s， 0.183 s and 10.35 s， respectively. It shows that the proposed Adam optimization algorithm can effectively improve the training accuracy and convergence speed of LSTM model. With relatively small prediction errors， it can provide data support and prediction methods for environmental protection departments to make related air quality decisions.

Keywords：

applied mathematics; grey correlation; fuzzy comprehensive evaluation method; Adam; LSTM; air quality prediction

钟南山院士曾于2016年在医学权威杂志《柳叶刀》上刊发了一篇文章，重点阐述了空气污

染对呼吸道疾病的严重影响[1]。尤其每到冬季，北方很多城市污染加重，雾霾天气高频出现，不仅威胁着人们的身体健康，而且也给人们日常出行活动带来了极大的困扰。为了更好地对空气污染进行监控和治理，科学有效地對空气质量进行分析预测具有重要意义。2020年初，新冠疫情爆发，山西省启动重大突发公共卫生事件一级响应，太原市采取企业停工、机动车停驶等一系列举措，人们发现2020年2月份太原市的空气质量明显好于以往。因此，可将这次疫情防控时期作为进一步探究影响城市空气质量变化主要因素的良好时间段。

近年来，国内外都越来越重视对空气质量的研究，不断开展对空气质量的分析评价及预测。伊元荣等[2]提出用灰色聚类法对乌鲁木齐市（简称乌市，下同）空气质量状况进行了研究，结果表明乌市大气质量状况变化总体较稳定并向清洁程度发展，但建立的白化函数易使评价结果出现偏差。普映娟等[3]用指数评价法对保山市的空气质量进行了评价，评价结果和实际环境情况比较吻合，但指数评价法只适用于短期评价。潘本锋等[4]用层次分析赋权法对城市的空气质量进行了排名，反映了不同城市间的空气质量状况差异，但用绝对值计算标度，得到的结果误差较大。在空气质量预测方面，牟敬锋等[5]建立ARIMA模型对深圳市空气质量指数进行了预测，取得良好的预测效果，但是随着天数增多，预测精度将大大下降。唐之享[6]通过运用BP神经网络学习空气污染物数值的统计规律实现对空气质量的预测，但是BP易出现过拟合及局部最小化问题。郑洋洋等[7]利用SARIMA-SVR组合预测模型得到的空气质量预测结果精度较高，稳定性较好。张冬雯等[8]针对空气质量研究中预测精度低的问题，提出了基于LSTM的神经网络模型对DELHI市和HOUSTON市的空气质量进行了预测，有效提高了预测精度。

为了解决上述研究中所存在的问题，本文提出用基于灰色关联度法的模糊综合评价法和基于Adam优化的LSTM时间序列预测模型对太原市空气质量变化趋势进行评价及预测，为太原市大气污染评价与治理提供参考。

1 模糊灰色关联综合评价法

1.1 评价方法分析

模糊综合评价法[9]与较为常用的空气质量评价方法相比，能较好地满足大气中各种污染因子的随机性和模糊性，得到的评价结果更为清晰。但是，在评价过程中得到的权重过于片面，会导致评价的结果偏差过大。而灰色关联度法[10]是一种科学高效的方法，它采取对现有实际数据合理的处理，达到对系统发展趋势的科学描述，继而明确权重值，可以解决结果偏差过大的问题。因此，本文对太原市空气质量的评价采用基于灰色关联度法的模糊综合评价法，通过将灰色关联度思想和专家评判法相融合以增加确定评价指标权重的客观准确性，从而作出更为精准的评价。

1.2 评价步骤

1.2.1 确定因子集

设空气质量评价有n个评价因子，确定因子集U=u1，u2，…，ui，…，un，其中ui（i=1，…，6）表示PM2.5，PM10，SO2，NO2，CO和O3这六个关键性的评价因子。

1.2.2 确定评语集

确定评语集V=v1，v2，…，vk，…，vj，在这里空气质量评价的结果分别表现为优、良、轻度、中度、重度和严重。

1.2.3 确定隶属函数

根据《环境空气质量标准》（GB 3095—2012），确立隶属度矩阵Ut=uijtM×N，uij代表了第i种因子对于第j级空气质量的隶属度。

1.2.4 灰色关联度法求解因素权重

确定完评判矩阵R和因子权向量W后，得到最后的空气质量综合评价结果矩阵为

B=At·Ut=AtUt=

B1t，B2t，…，BNt。（1）

2 LSTM递归神经网络

LSTM[11]是以RNN[12]为基石，采用“门”结构解决序列数据问题的改进后循环神经网络，每个数据段与前一段有一定的相关性。由于前一时刻的信息神经元将与当前的信息神经元相连，利用LSTM内部的门可以解决对数据的长期依赖。因此，LSTM拥有很强的记忆能力，可以更为高效地处理时间序列的预测及分类。而空气质量数据是通过指定时间点定时监测到的时间序列数据，未来的空气质量数据和其历史数据有着较强的关联性，因此，LSTM适用于对空气质量进行预测[13]。

在LSTM中，每个神经元包含3个门：输入门、遗忘门和输出门。输入门是确定在神经元状态下要记住哪些新的信息内容。遗忘门是确定要从单元状态中忘记哪些数据信息。输出门是确定在神经元状态下要输出哪些信息。具体如图1所示。

核心算法公式如下：

ft=σWfht-1，xt+bf，（2）

St=11+e-t，（3）

Ct=ft·Ct+it·C～t，（4）

it=σWi·ht-1，xt+bi，（5）

C～t=tanhWC·ht-1，xt+bC，（6）

Ot=σW0·ht-1，xt+b0，（7）

ht=Ot·tanhCt。（8）

3 Adam算法

自适应矩估计算法[14]（adaptive moment estimation，Adam）是AdaGrad 和RESProp算法的结合，它作为一个搜索系统最优化目标的算法，加入了二次方梯度改良，不仅对原始平方梯度的指数减弱平均值加以保存，还维系了原始梯度的指数减弱平均值，能够对各参数的自适应学习率进行计算，较适合优化LSTM模型，同时适用于像空气质量这样的较大数据集，可以利用类似权值的参数降低LSTM对空气质量的预测误差，进而提高LSTM预测模型的精度。

Adam更新参数方法如下。

随机挑选x（1），x（2），…，x（i），…，x（m）m个样本，x（i）对应y（i），计算fθ对θ的梯度：

gt←1mSymbolQC@θt-1∑iLftx（i）;θt-1，y（i）。（9）

計算一阶矩及梯度二阶距：

mt←β1·mt-1+1-β1·gt，（10）

vt←β2·r+1-β2·g2t。（11）

修正一阶矩mt，二阶矩vt：

m^t←mt1-βt1，

v^t←v^

t1-βt2。（12）

最后可得参数更新公式：

Δθt← -ηmt^v^t+δ，θt←θt-1+Δθt。（13）

4 实验与分析

4.1 空气质量评价结果与分析

4.1.1 数据来源及预处理

本次空气质量评价的数据来源于中华人民共和国环保部数据中心实时发布的有关太原市空气质量数据，取样时间为2019-12-25至2020-01-24日疫情防控前的时间段以及2020-01-25至2020-02-24一级应急响应防控期间，数据共计62组。依照最新发布的《环境空气质量标准》（GB 3095—2012），本文的空气质量评价采用细颗粒物（PM2.5）、可吸入颗粒物（PM10）、二氧化硫（SO2）、二氧化氮（NO2）、臭氧（O3）和一氧化碳（CO）这6项与AQI密切相关的指标，评价等级划分为优、良、轻度污染、中度污染、重度污染、严重污染6个等级，空气质量指数级别分布如表1所示。

本次空气质量评价的各个指标值都不在一个维度上，因此利用MATLAB中的mapminmax函数对原始数据进行归一化处理。通过多次的仿真实验，发现归一化区间设置为[0，1]时，空气质量的评价效果最好。

4.1.2 评价结果分析

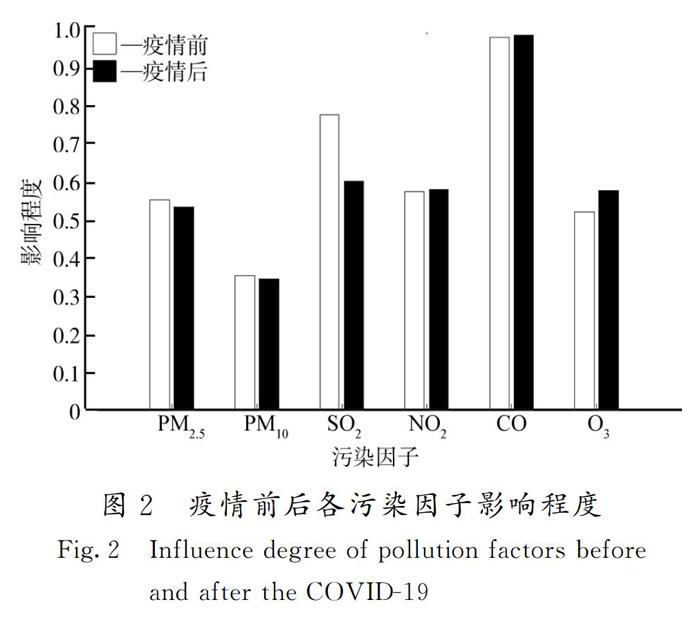
按照本文所述评价模型对2019-12-25到2020-01-24太原市实施强管控措施前以及2020-1-25至2020-02-24太原市实施强管控措施期间的空气质量进行评价，可得影响空气质量的各污染因子影响程度，如图2所示。

从图2可以看出，在2020-01-25到2020-02-24，太原市实施强管控措施后，SO2的污染程度明显降低，PM2.5和PM10的污染程度略显降低，NO2和CO的污染程度基本和之前持平。对这一时期的空气质量进行评价，结果如图3所示。

从图3的空气质量评价结果可以看出，在太原市一级应急响应前，太原市的空气质量主要处于三级到六级的等级标准，而在一级应急响应的1个月，太原市的空气质量指数级别（以下简称空气质量等级，下同）明显下降，主要处于一级到三级的等级标准。通过对图2和图3的综合分析，可以看出，在太原市一级应急响应疫情防控加强期间，人们居家隔离，减少机动车辆出行，以及春节期间各工厂停工，对空气质量的好转起到一定成效。但是受季节、气象等因素（包括春节期间烟花爆竹的燃烧[15]以及供暖燃煤等）的影响，其他污染物的影响并未下降。总的来说，大面积的居家隔离和出行、生产行为的减少对太原市空气质量的改善起到了积极作用，当然上述的分析仍需要更多的证据加以佐证。

4.2 基于Adam-LSTM的空气质量预测模型

4.2.1 数据来源及分析

本次预测数据同样来源于中华人民共和国环保部数据中心实时发布的太原市空气质量数据，取样时间为2016-01-01至2020-02-29，数据共计1 522组。AQI的历史序列值具备着特性明显的周期性，同时季节变化极其鲜明。此外它的历史序列值存在着线性和非线性分量[16]。对于通常的预测模型而言，它们对AQI数值的预测效果没那么明显。对此，本文使用Adam优化后的LSTM时间序列模型对空气质量的等级进行预测，为进一步精确预测AQI的走向提供了切实有效的参考依据。

4.2.2 模型的实现过程

基于Adam-LSTM空氣质量预测模型的建模过程如下。

1）获取AQI序列，依据预测要求，对AQI序列划分窗口。经归一化处理将数据标准化，并建立LSTM预测模型。

2）利用Adam算法训练LSTM，预测下一个窗口的值，输出值与真实值间的误差会反向影响参数值，伴随着每次输入，误差会以一定的速度下降，直至达到期望值。通过Adam算法在此阶段进行优化，提高模型的收敛速度。

3）预测窗口向后滑动推进，通过每次迭代降低历史序列中的随机波动影响，以达到更精确的预测。

模型实现过程的流程图如图4所示。

4.2.3 预测结果及分析

鉴于超过6天的AQI数据对第7天的AQI数据影响较小，因此模型利用前6天AQI数据对第

7天的AQI数据进行预测，向后滑动推进进行优

化预测。本文首先用LSTM进行预测，再将其与Adam-LSTM预测结果进行对比。经过迭代训练后，得到2种预测模型的Error-Cost散点图，如图5所示。

从图5中可知，2种模型在迭代过程中，随着迭代次数增加，均方误差都不断降低，且在结束10次迭代后，均方误差都达到最低。可以看出Adam-

LSTM模型的预测性能要优于LSTM模型，说明Adam算法优化后的LSTM模型具有更高的预测精度。

表2列出了2种模型的预测误差指标，即均方根误差（RMSE）可以用来判断模型的预测精度，由表2可得Adam-LSTM模型的RMSE值为0.183，低于LSTM模型的RMSE值0.203，也说明了Adam优化后的LSTM在预测精度上有了明显的提升，可以作为一种有效的预测方法。

将2种预测模型的预测结果和真实值进行对比，如图6和图7所示，

从图6和图7中可以看出，Adam优化后的LSTM模型对原始数据的拟合度比LSTM模型好，预测效果也更好。

根据图7预测结果可得，后者预测的太原市的空气质量等级几乎接近于实际值，且真实等级和预测等级基本符合同一波动，预测精度较好，具有较高的精准度。但是该预测模型对于空气质量等级的预测依旧存在一定的误差，这需要更进一步的研究探索。另外通过污染等级预测模型的曲线走势不难看出，在2016年-2020年，AQI的变化呈现出先降后增的趋势，在时间线上正好对应了每一年的年初与年末，这一关键信息对于太原市空气污染的整体防控和治理也提供了事实理论参照。

5 结 语

本文针对太原市疫情防控期前后的空气质量的评价问题，构建了基于灰色关联度法的模糊综合评价模型，并在空气质量评价的基础上，针对空气质量等级的预测问题，分别构建了LSTM模型和Adam-LSTM时间序列预测模型。

1）根据基于灰色关联度法的模糊综合评价模型所得的评价结果不仅可以反映空气质量中污染浓度较高的污染物因子，而且也能反映其他浓度较小的污染物的变化情况。该模型的结果对太原市空气质量的评价是遵循事实依据的，结果显示疫情期间太原市采取严控措施后，空气污染水平显著降低。

2）根据LSTM和Adam-LSTM时间序列预测模型预测的结果，可知2种模型都能够有效地捕捉大气污染的长期时间机制，可以从AQI历史数据中提取有用的内在特征，预测效果符合预期，可以为太原市居民们的出行提供健康指导。与LSTM模型相比，Adam优化后的LSTM时间序列预测模型通过类似权值的参数降低了LSTM模型的预测误差，预测精度更高。

本研究成果可为太原市长期的空气污染防治攻坚行动提供决策支持。

但研究也存在不足之处，本文所选取的样本数据，仅限于疫情防控前后的时间段，若再选取历年未发生新冠肺炎的春节期间数据进行评价对比，则会更有说服力，并可更好地帮助人们掌握影响城市空气质量的因素。在对空气质量等级的预测中，缺乏对污染物扩散、气象环境、气候背景等诸多因素与太原市AQI指数关系的探讨，只是通过AQI值对空气质量等级进行了预测。在以后的研究中，将开展各类影响因素对空气质量的影响预测研究，提高对空气质量预测的精度。

参考文献/References：

[1] GUAN Weijie， ZHENG Xueyan， CHUNG Kianfan， et al. Impact of air pollution on the burden of chronic respiratory diseases in China： Time for urgent action[J]. The Lancet， 2016， 388（10054）：1939-1951.

[2] 伊元荣，海米提·依米提，艾尼瓦尔·买买提，等.基于灰色聚类法的乌鲁木齐市空气质量状况研究[J].水土保持研究，2007，14（6）：139-141.

YI Yuanrong， YIMITI Haimiti， MAIMAITI Ainiwaner， et al. The atmospheric quality status research based on gray clustering method in Urumqi[J].Research of Soil and Water Conservation， 2007， 14（6）：139-141.

[3] 普映娟，王琳邦.环境空气质量综合指数评价方法探讨[J].环境科学导刊，2010，29（2）：93-94.

PU Yingjuan， WANG Linbang. Discussion on comprehensive index assessment method of environmental air quality[J].Environmental Science Survey，2010，29（2）：93-94.

[4] 潘本锋，杜丽，李莉娜.層次分析赋权法在城市空气质量排名中的应用[J].中国环境监测，2015，31（2）：44-47.

PAN Benfeng， DU Li， LI Lina. The study on applications of determining weight vector based on ahp for ranking ambient air quality of city[J].Environmental Monitoring in China， 2015， 31（2）： 44-47.

[5] 牟敬锋，赵星，樊静洁，等.基于ARIMA模型的深圳市空气质量指数时间序列预测研究[J].环境卫生学杂志，2017，7（2）：102-107.

MOU Jingfeng， ZHAO Xing， FAN Jingjie， et al. Time series prediction of AQI in Shenzhen based on ARIMA model[J].Journal of Environmental Hygiene，2017，7（2）：102-107.

[6] 唐之享.基于BP神经网络的空气质量预测研究与实现[D].西安：西安电子科技大学，2018.

TANG Zhixiang. Research on and Implementation of Air Quality Prediction based on BP Neural Network[D].Xi′an： Xidian University， 2018.

[7] 郑洋洋，白艳萍，续婷.基于SARIMA-SVR组合模型的空气质量指数预测[J].河北工业科技，2019，36（6）：436-441.

ZHENG Yangyang， BAI Yanping， XU Ting. Air quality index prediction based on SARIMA-SVR combined model[J]. Hebei Journal of Industrial Science and Technology， 2019，36（6）：436-441.

[8] 张冬雯，赵琪，许云峰，等.基于长短期记忆神经网络模型的空气质量预测[J].河北科技大学学报，2020，41（1）：67-75.

ZHANG Dongwen， ZHAO Qi， XU Yunfeng， et al.Air quality prediction based on neural network model of long short-term memory[J]. Journal of Hebei University of Science and Technology，2020，41（1）：67-75.

[9] 罗运成.基于模糊综合评价模型的城市空气质量评价研究[J].环境影响评价，2018，40（5）：79-83.

LUO Yuncheng. Research on urban air quality evaluation based on fuzzy comprehensive assessment method[J].Environmental Impact Assessment，2018，40（5）：79-83.

[10]吴先明，蔡海滨，邓鹏.基于灰色关联度的改进TOPSIS模型在水质评价中的应用[J].三峡大学学报（自然科学版），2018，40（2）：24-28.

WU Xianming， CAI Haibin， DENG Peng. Application of improved TOPSIS model based on grey correlation grade to water quality evaluation[J]. Journal of China Three Gorges University（Natural Sciences），2018，40（2）：24-28.

[11]WAN Huaiyu， GUO Shengnan， YIN Kang， et al. CTS-LSTM： LSTM-based neural networks for correlatedtime series prediction[J]. Knowledge-Based Systems， 2020.DOI： 10.1016/j.knosys.2019.105239.

[12]楊丽，吴雨茜，王俊丽，等.循环神经网络研究综述[J].计算机应用，2018，38（sup2）：1-6.

YANG Li， WU Yuxi， WANG Junli， et al.Research on recurrent neural network[J].Journal of Computer Applications，2018，38（sup2）：1-6.

[13]张春露，白艳萍.基于TensorFlow的LSTM模型在太原空气质量AQI指数预测中的应用[J].重庆理工大学学报（自然科学），2018，32（8）：137-141.

ZHANG Chunlu， BAI Yanping. Application of LSTM prediction model based on Tensor Flow in Taiyuan air quality AQI index[J].Journal of Chongqing University of Technology （Natural Science），2018，32（8）：137-141.

[14]张晋晶.基于随机梯度下降的神经网络权重优化算法[D].重庆：西南大学，2018.

ZHANG Jinjing. Optimization Algorithms of Neural Networks Weights Based on Stochastic Gradient Descent[D].Chongqing： Southwest University，2018.

[15]曹馨元，何月欣，陈卫卫，等.烟花爆竹禁燃对春节期间东北地区空气质量影响评估[J].中国环境监测，2018，34（4）：77-84.

CAO Xinyuan， HE Yuexin， CHEN Weiwei， et al. Effects of fireworks forbidden on air quality during the Spring Festival in Northeast China[J].Environmental Monitoring in China，2018，34（4）：77-84.

[16]李博群，贾政权，刘利平.基于模糊时间序列的空气质量指数预测[J].华北理工大学学报（自然科学版），2018，40（3）：78-86.

LI Boqun， JIA Zhengquan， LIU Liping. Air quality index forecast based on fuzzy time series models[J].Journal of North China University of Science and Technology （Natural Science Edition），2018，40（3）：78-86.

收稿日期：2020-06-22;修回日期：2020-12-01;责任编辑：王海云

基金项目：国家自然科学基金（61774137）;山西省自然科学基金（201701D22111439， 201701D221121）;山西省回国留学人员科研项目（2016-088）

第一作者简介：曹 通（1995—），男，山西临汾人，硕士研究生，主要从事现代优化算法理论及应用方面的研究。

通讯作者：白艳萍教授。E-mail： baiyp666@163.com

曹通，白艳萍.太原市COVID-19防控前后空气质量分析及预测[J].河北工业科技，2021，38（2）：156-162.

CAO Tong，BAI Yanping.Air quality analysis and prediction before and after the prevention and control of COVID-19 in Taiyuan[J].

Hebei Journal of Industrial Science and Technology，2021，38（2）：156-162.