基于自相关侧峰消除的北斗B1C快速高精度捕获算法
许 睿,唐瑞琪,罗 凯,曾庆化,刘建业
(南京航空航天大学 自动化学院,南京 211106)
我国北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)第三代民用信号新增B1C 信号[1],该信号采用二进制偏移载波(Binary Offset Carrier,BOC)调制方式[2],伪随机码周期为10 ms[3],能够与现存导航信号共享频点,又能提高信号跟踪精度与定位精度。
然而与传统的采用相移键控调制方式的导航信号(如,GPS L1 C/A 信号)相比,BOC 调制信号自相关函数具有多峰特性,会在接收机信号捕获和跟踪阶段带来模糊性问题[4],即信号自相关主峰旁存在若干副峰,接收机有可能捕获或跟踪在副峰上,造成误捕和误锁,若不进行处理会进一步导致定位结果不稳定或出现较大偏差。自2002年Betz.J.W[4]系统地提出BOC 调制以来,典型的BOC 调制信号多峰消除去模糊算法可分为三类。第一类是边带滤波法,也称为BPSK-Like 算法[5],通过频域滤波将BOC 调制信号频谱上两个主波瓣提出,再作为类BPSK 信号频谱处理,这种方法会降低BOC 调制带来性能优势,且需要额外的滤波器资源。第二类为峰跳法,即Bump-Jump(BJ)方法[6],该方法需要额外的相关器通过对比第一副峰与主峰的大小来判定捕获的点是否在主峰上,需要经过多次采样计算,新增的相关器涉及大量的加乘运算增加硬件开销,且在信噪比较低的情况下会出现判决错误的现象。第三类是自相关副峰消除技术[7,8],通过设计不同的相关函数并按照一定的组合方式进行合成,从而消除主峰之外的所有副峰实现无模糊捕获,不需增加大量运算和新的硬件,灵活性更大。
除多峰性问题,北斗B1C 信号采用10 ms 周期的伪随机码,码周期的增加对应信号跟踪阶段的积分时间的增长,这有助于减少噪声,提高跟踪精度和伪距估计精度,但同时跟踪环路的带宽需要相应地降低,这又会导致跟踪环路牵引范围变窄,因此,跟踪环路初始值就需要更准确,这对提供跟踪环路初值的捕获阶段提出了更高精度的要求。此外,较长的码周期也增加了捕获运算量与耗时。对于北斗三号B1C 接收机而言,要实现信号的快速准确跟踪与定位,就必须先进行快速捕获,并得到精度足够高的载波频率与码相位初值。接收机通常采用先粗捕获再精捕获的方法[9]平衡捕获的精度与速度,粗捕利用FFT 算法实现对频率和码相位搜索的并行计算得到粗略的多普勒频率与码相位,精捕则可通过对FFT 输出序列进行SINC 拟合来获得更精确的多普勒频率估值[10]。但对于采用BOC 调制的信号来说,由于副载波的存在会影响SINC 拟合的效果,导致精捕获得到的频率误差较大,从而会使得信号跟踪失败。鉴于此,本文针对北斗B1C信号设计了一种快速高精度捕获算法,先是基于降采样和多级搜索的方式,通过减少数据点,快速实现了对信号的粗捕获并将对多普勒频移的估计误差缩小到一定范围,大大减少了信号捕获的计算量,有效提高了B1C 信号的捕获速度;再通过多项式曲线拟合来估计频率相对于相关值的峰值点,实现了多普勒频移的高精度捕获,并有效避免了副载波对精捕获的影响。最后基于真实信号的实验结果验证了该算法对捕获精度和速度的提升。
1 B1C 信号与ASPeCT 算法
1.1 B1C 信号的数学模型
北斗B1C 信号的载波频率为1575.42 MHz,与GPS L1 和Galileo E1 共享频点,带宽为32.736 MHz,包含两个正交分量:数据分量与导频分量。数据分量由导航电文和测距码经副载波调制产生,调制方式为正弦BOC(1,1)调制;导频分量由测距码经副载波调制产生,采用QMBOC(6,1,4/33)调制,其功率是数据分量功率的3 倍。除使用子载波外,导频分量还使用周期为18 s、码长度为1800 码片的子码来调制测距主码,每个子码码元持续时间为10 ms,与测距主码的周期相等,也与数据分量中导航电文的一位(bit)所持续时间相同。导频分量采用的QMBOC 调制方式将BOC(1,1)分量和BOC(6,1)分量按照29:4 的功率比调制在相互正交的副载波上加以实现。整个B1C信号实际包含了三个实分量[4],如式(1)所示。
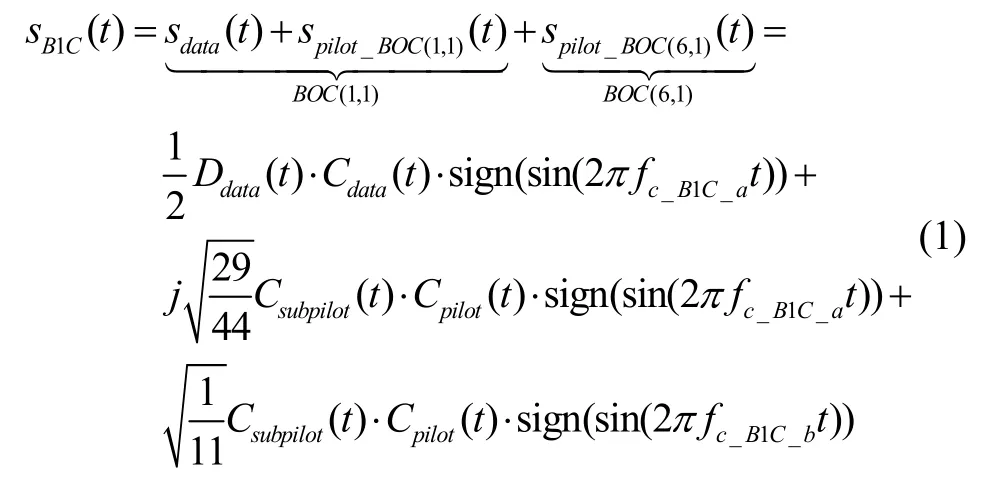
B1C 信号的BOC(1,1)为低频分量,是信号的窄带部分;BOC(6,1)为高频分量,是信号的宽带部分。BOC(1,1)分量包含完整的信号结构,功率也较BOC(6,1)分量更大,因此常规处理GPS L1 C/A 的窄带接收设备也可以接收到北斗B1C 信号。以一颗星信号为例,北斗B1C 信号在窄带接收机中的中频信号可写为:
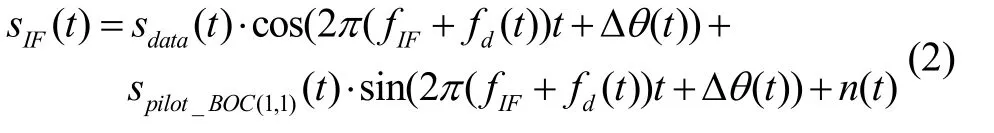
根据式(2),窄带接收机接收到的北斗B1C 信号可近似认为仅包含BOC(1,1)调制信号部分。其自相关函数表示为:
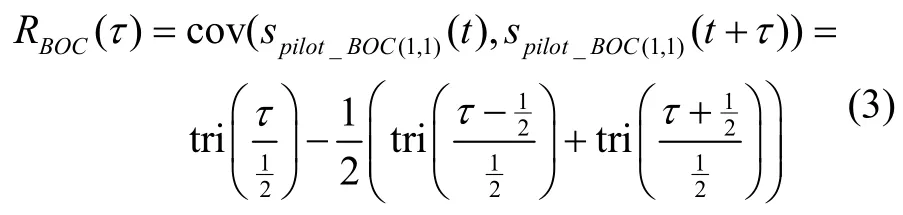
式中:τ表示以码片为单位的码延时,代表相关函数,代表三角函数。如图1所示,其自相关峰主峰较为尖锐,具有良好的测距性能,但存在副峰,会导致误捕和误锁,需要对副峰进行处理以消除其不利影响。
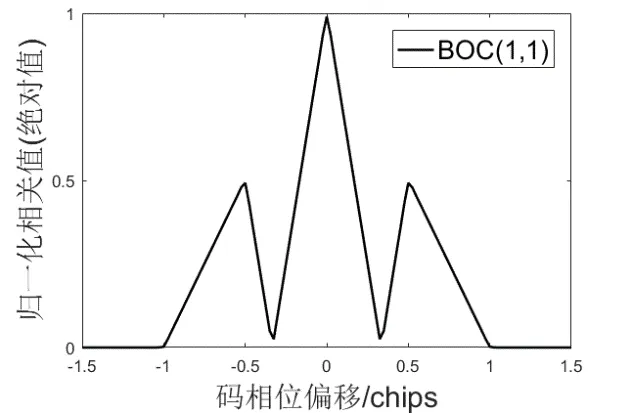
图1 BOC(1,1)调制方式下的自相关函数Fig.1 Autocorrelation function in BOC(1,1)modulation
1.2 自相关侧峰消除捕获算法
对于BOC(n,n)类调制信号可以使用自相关侧峰消除( Autocorrelation Side-Peak Cancellation Technique,ASPeCT)算法消除副峰,其原理是:首先将本地生成的PRN 码(测距码)分成两组,一组使用副载波进行调制得到BOC 信号,另一组不作处理为原始PRN 信号,然后将这两组本地码分别与经过混频器处理后的信号作相关运算,对于BOC(1,1)调制信号而言,得到的信号自相关函数如式(3)所示,其与测距码的互相关函数表示为:
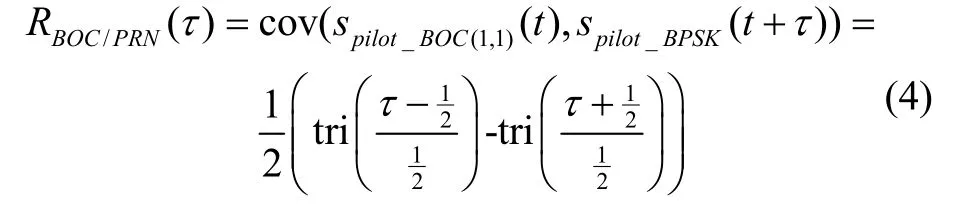
再将两个相关函数进一步组合,使用二者的平方差构建出一个新的相关函数,即:
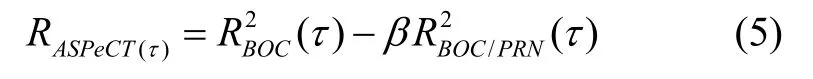
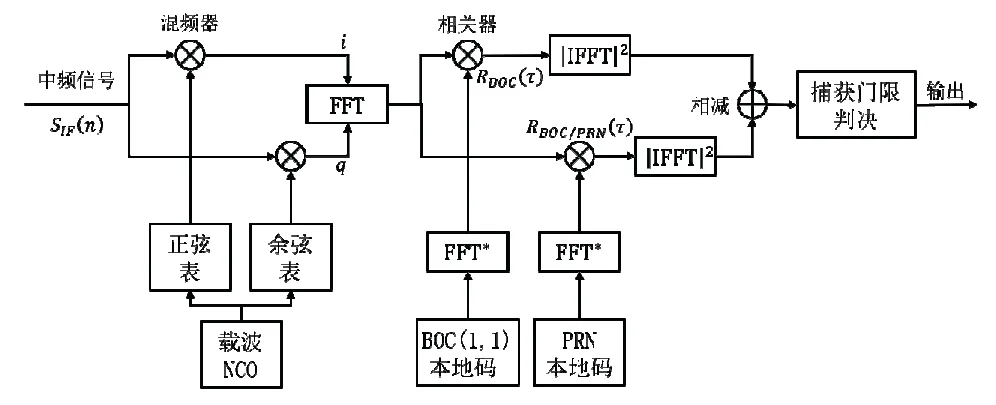
图2 BOC(1,1)信号的ASPeCT 算法捕获原理Fig.2 Acquisition principle of ASPeCT algorithm for BOC(1,1)signal
当接收的中频信号分别与i支路和q支路上的正弦和余弦载波信号混频后,将得到的复数形式的混频结果进行FFT 变换,然后将其分别与BOC(1,1)和PRN本地码FFT 变换的共轭值相乘,再分别作IFFT 变换后取平方差,得到的值即为ASPeCT 算法所构造的相关值,若峰值超过捕获门限值,则接收机捕获到了信号,并得到该信号的频率和码相位两个参数值。
2 快速高精度捕获算法
基于ASPeCT 算法可以解决BOC 信号自相关多峰特性带来的误捕问题,从而能顺利实现北斗B1C 信号的粗捕获过程。但粗捕得到的多普勒频移估计误差较大。若要使得接收机能够实现信号的快速稳定跟踪,则需要对载波频率进行较为精确的估计,即进行精捕获。由于B1C 信号中副载波调制的存在,影响了传统精捕获算法中SINC 曲线拟合的效果,导致精捕获得到的频率误差较大,从而可能会导致跟踪失败。此外,北斗B1C 信号的一个伪码周期为10 ms,包含10230个码片,与传统GPS 中C/A 码每周期1 ms 对应1023个码片相比,从周期长度和序列长度上都增加到10倍。这给信号捕获带来了更高的计算量,相同条件下完成卫星信号捕获势必要花费更多时间。因此,需要在捕获算法的精度与效率上同时改进。
鉴于此,本文设计了一种快速高精度捕获算法,首先基于多级搜索和降采样策略快速将信号的频率捕获缩小到一个较小的范围,再通过多项式曲线拟合算法,实现对B1C 信号多普勒频移的高精度捕获。该算法的整体逻辑思路如图3所示。
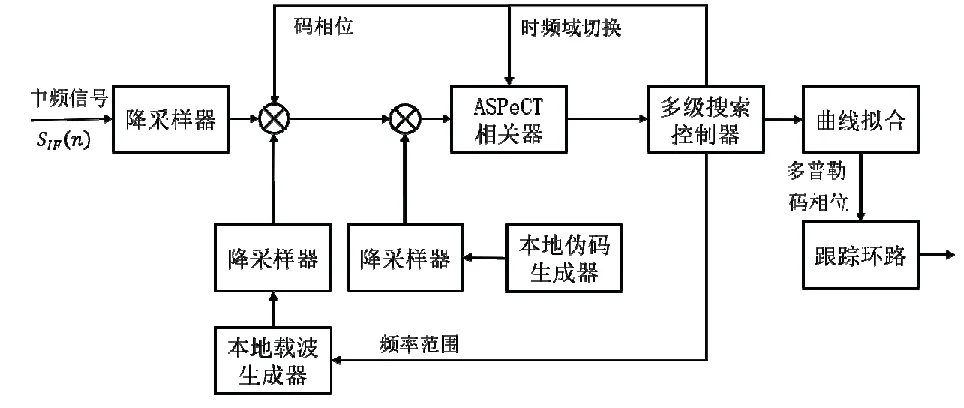
图3 针对B1C 信号的快速高精度捕获算法框图Fig.3 Block diagram of fast and high-precision acquisition algorithm for B1C signal
2.1 多级搜索控制
多级搜索的目的是将对信号频率的搜索快速缩小到一个较小的范围之内,以便于使用曲线拟合的方法对频率进行更加精确地估计。多级搜索的思路如图4所示。
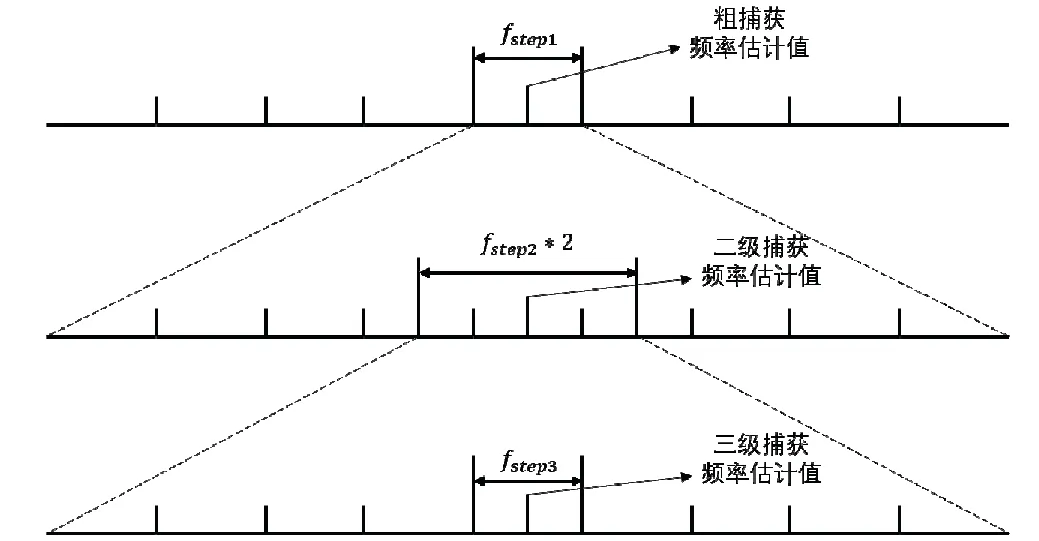
图4 频率多级搜索示意图Fig.4 Schematic diagram of frequency multilevel search
多级搜索的级数与每级搜索的步长共同影响捕获算法的运算量,为了达到更好的曲线拟合效果,最终搜索步长设为5 Hz,以达到更为精确的频率估计值。而一级搜索步长则需要在确保频率估计值落在正确范围之内的基础上尽量选择较大的值,以此减少一级搜索的次数。为了降低漏警发生的概率,接收机通常应当对于频率误差绝对值的设置不得超过表示相干积分时间,从而得到频率搜索步长的取值范围为:

北斗B1C 信号的伪码周期为10 ms,这就意味着该信号在接收机捕获环节的相干积分时间最少应为伪码单周期的10 ms,从而得到应当不超过88.6 Hz,即当频率误差大于44.3 Hz 时,漏警事件的概率将会逐渐提升。故可设置为80 Hz,相应的级数与搜索次数对应关系如表1所示,搜索范围为7.4 kHz。
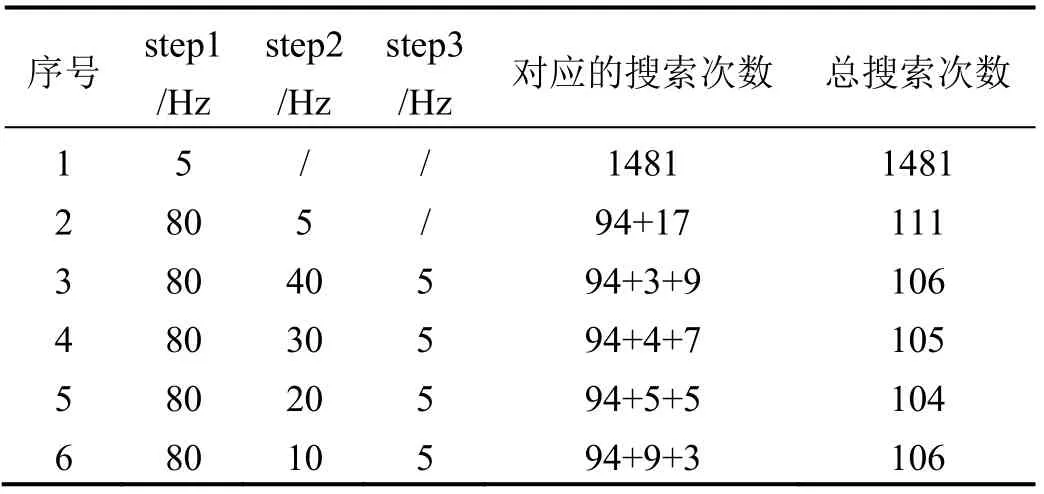
表1 不同步长下的搜索次数统计Tab.1 Statistics of search times under different step size
由表1 可得,三级搜索且二级搜索步长在30 Hz和20 Hz 时的总搜索次数分别为105 次和104 次,而20 Hz 时三级搜索的搜索次数只有5 次,考虑到精捕阶段希望有较多数据点以供多项式拟合使用,则30 Hz 的二级搜索步长更为合适,故三级搜索的步长应该分别设置为80 Hz、30 Hz 和5 Hz。
基于此多级搜索策略,可以进一步使用时频域结合搜索的方法优化算法的结构。考虑到三级搜索每一次均进行了频率与码相位在频域的并行搜索,而三次搜索的码相位基本一致,即一级搜索的码相位已较为精确,之后的码相位搜索工作是重复的,所以理论上可以省去后两次的码相位搜索来减少计算量。在具体实现上,将初次搜索得到的码相位作为后两次搜索读入信号的起始点,将后两次的频域并行搜索改为时域的频率单独搜索,以便极大地减少了后两次搜索的计算量。
2.2 降采样策略
基于降采样的信号快速捕获算法的思路是使用数据预处理的方法,通过缩短输入数据与本地码的长度来减少计算量,从而使得信号捕获速度加快。首先在本地伪码生成环节,按照前端设备的采样频率生成伪码数据后以固定倍数进行降采样,即按照每隔固定长度数据量取一个数据点的规律,利用取出的数据点生成新的序列,从而实现伪码数据的降采样处理。同样地,在中频数据读入环节也要按照相同的规律进行数据处理,从而保证中频数据和本地码的对应关系,再利用降采样后的数据进行信号捕获时就可以节省大量的计算。
降采样实质是对已采集信号的二次抽样,抽样后不仅信号的采样频率降低,实际中频频率也对应改变。研究中所采用的前端设备,采样频率16.368 MHz,中频频率4.092 MHz,非正交采样。当二次抽样倍数为偶数倍时,降采样后的数据中频降至零中频,非正交采样导致频谱混叠,则捕获算法无法获得正确的多普勒频率。实验也表明,在对数据进行二倍降采样或者四倍降采样之后,由于偶数倍降采样处理后数据的固定特征点损失,捕获结果中会出现两个可能的峰值,且二者的载波频率关于中心频率对称,即多普勒互为相反数。这就带来了很大的误捕风险。因此需要采用奇数倍的降采样倍数,再考虑到采样频率过低会出现信号失真的问题,故使用三倍降采样进行数据预处理较为合适。图5 展示的就是对本地伪码进行三倍降采样的思路。相应地,接收机读入的中频数据也要进行相同规律的处理。
图5 中,变量N 代表的是在前端采样频率下测距码一个完整周期的采样点数。式(2)中的中频信号离散化后得到处理,新的中频信号为其中通过三倍降采样 其中m=1,2,3...N/3。降采样后的数据序列长度缩短到原始长度的三分之一。
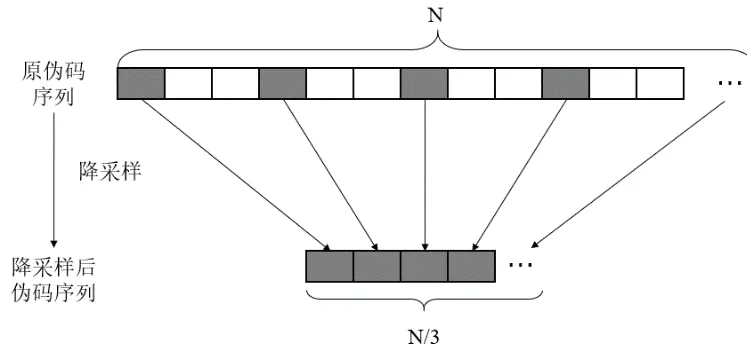
图5 伪码降采样示意图Fig.5 Schematic diagram of PRN code downsampling
结合2.1 节的多级与时频域切换搜索策略,接收机输入的中频信号和本地伪码经过同样的降采样处理后,首先是粗捕获通过FFT 在频域中对频率和码相位进行并行搜索,然后控制器记录一级搜索得到的码相位并将相关器切换到时域,同时控制本地载波的频率搜索范围和输入信号的起点,只进行二级与三级的频率搜索。这样使得整个捕获过程中的计算量大大减少,可将捕获速度提高到三倍左右。具体思路如图3所示。
在整个捕获过程中,最耗费时间的是搜索过程中的FFT 运算。假设中频数据一个完整伪码周期的采样点数为N,一个数据点的FFT 运算量为M,精捕获算法和快速精捕获算法的FFT 运算量如表2所示。

表2 运算量对比Tab.2 Comparison of calculation quantity
由表2 可以得到,与单独的精捕获算法相比,使用降采样与时频域切换操作的快速精捕获算法将占据主要计算量的FFT 运算相对减少了70.16%,考虑到算法中的其他运算,整体计算量减少比例会略低于该值。需要指出的是,降采样处理可以有效降低运算量,但也使得信号能量有少量损失,使得捕获灵敏度略有下降。
2.3 多项式曲线拟合
为增加后续跟踪环路的跟踪成功率,可以进一步提高多普勒频率估计精度。2.2 节中的多级搜索策略可以将载波频率估计缩小到一个较为精确的范围,而由于相关结果包含SINC 项,在小范围频率区域内可简化近似于抛物线,因此可采用一个二阶多项式曲线拟合,以提高频率估计精度,在拟合式选取拟合点数不易过多,以避免边界效应,本文中选取5 个点。

其中,
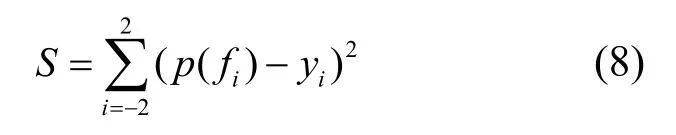
最后根据获得的拟合抛物线方程,求最大相关积分值,即曲线顶点所对应的频率f,该频率即为捕获获得的载波频率。以一组PRN40 通道的数据为例,绘制拟合前后的相关曲线如图6所示。
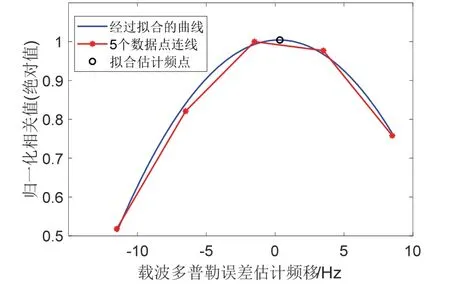
图6 二次多项式拟合多普勒Fig.6 Doppler frequency estimated by second-order polynomial fitting
由图6 可以看到拟合曲线与数据点连线较为贴切,很好地反映了相关值的变化趋势,图中标注的抛物线顶点相对应的频点即为多普勒频移的估计值。
3 实验验证与分析
为测试所提方法,使用前端采集器(iP-Solutions E2 GPS/Galileo L1 Front end)采集北斗B1C 真实信号进行测试,数据采集地点在无遮挡的楼顶,前端与采集数据主要参数如表3所示。

表3 采集的B1C 信号主要参数Tab.3 Main parameters of collected B1C signal
3.1 副峰消除效果分析
图7所示为ASPeCT 捕获算法解算B1C 真实信号( PRN40 ) 获得的码延时-多普勒频率图(Delay-Doppler Map,DDM),以及多普勒频率为-219 Hz 时的相关值变化曲线。
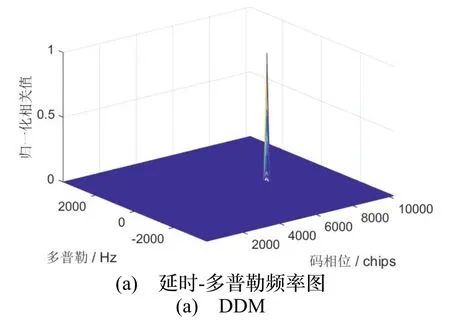
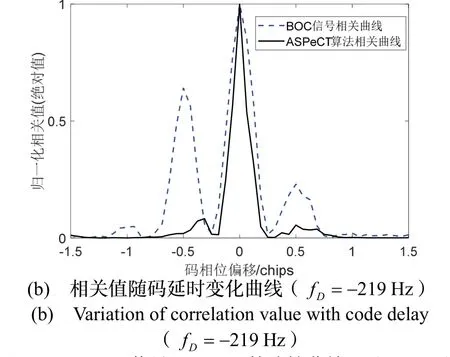
图7 BOC(1,1)信号ASPeCT 算法捕获结果(PRN40)Fig.7 Acquisition result of ASPeCT algorithm for BOC(1,1)signal(PRN40)
图7(a)显示该算法可以完成真实信号的捕获,与不使用ASPeCT 算法结果对比,如图7(b),副峰得到了很大程度上的削减,能够更有效地避免误捕。
表4 展示了采用ASPeCT 算法前后,从该数据中捕获到的6 颗卫星DDM 中的副峰主峰比。
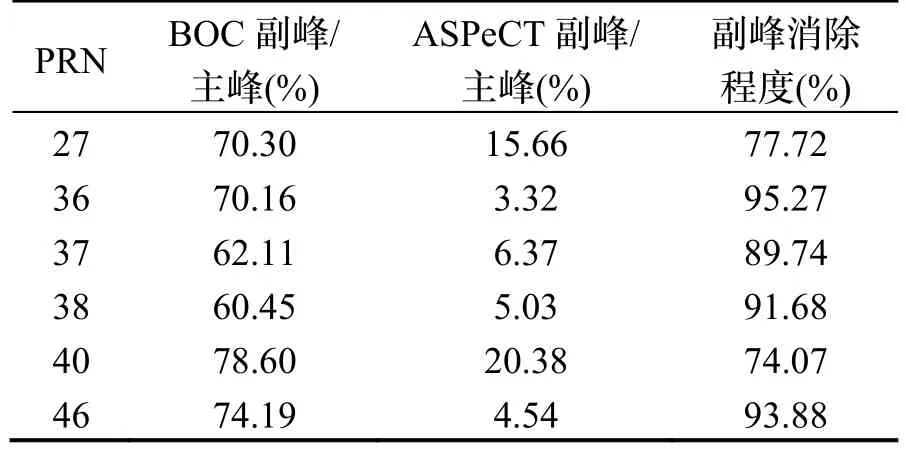
表4 采用ASPeCT 算法前后峰值对比Tab.4 Comparison of peak values before and after using ASPeCT algorithm
数据表明,北斗B1C 真实信号自相关曲线的副峰与主峰的平均比值约为69.30%,经过ASPeCT 算法处理之后该比值约降至9.22%,整体的副峰消除效果可以达到86.70%,消除了信号误捕的风险。
3.2 捕获速度对比
表5所示为采用本文所提快速精捕获算法和普通精捕获算法耗时对比表,捕获耗时使用MATLAB 统计,由于北斗卫星数量较多,仅列出捕获到卫星信号的通道耗时。
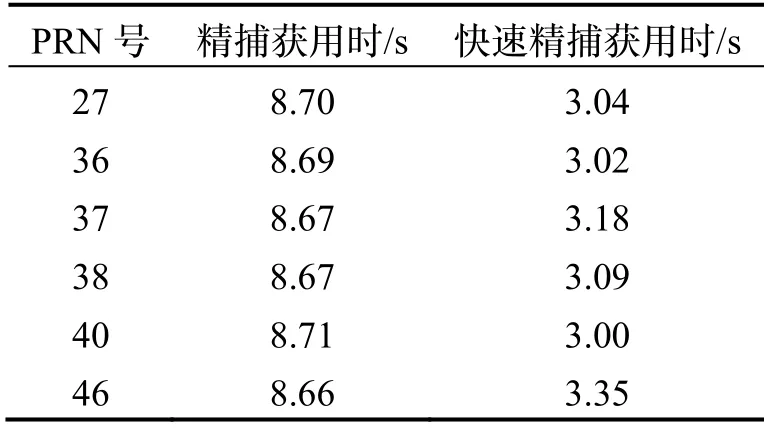
表5 快速精捕获算法速度对比表Tab.5 Speed comparison of fast fine acquisition algorithm
从表5 可以看出快速捕获算法耗时显著降低,普通精捕获算法单通道平均捕获用时8.68 s,而使用快速捕获算法后单通道平均用时3.11 s,实际捕获时间相对缩短了64.17%,较2.2 节分析的减少70.16%,FFT计算量略有降低,但考虑捕获还包含拟合等其他运算量,实际改进近2/3,仍然显著。
3.3 多普勒频率捕获精度分析
为分析快速精捕获算法获得的多普勒频率精度,利用锁相环输出的载波多频率频率拟合多普勒频率曲线,根据多普勒近似线性的变化规律,可以通过直线拟合来近似得到多普勒频率实际曲线,如图8所示。再根据拟合多普勒频率曲线获得的跟踪初始时刻多普勒频率值,即0 s 时刻的多普勒频率,作为捕获时刻的精确多普勒频率估计,则多频率频率的捕获误差即为捕获的多频率频率与跟踪初始时刻多普勒频率之差。图8所示为PRN40通道卫星多普勒频率跟踪结果,通过上述方法可得信号初始时刻的多普勒频率估计误差为0.63 Hz。
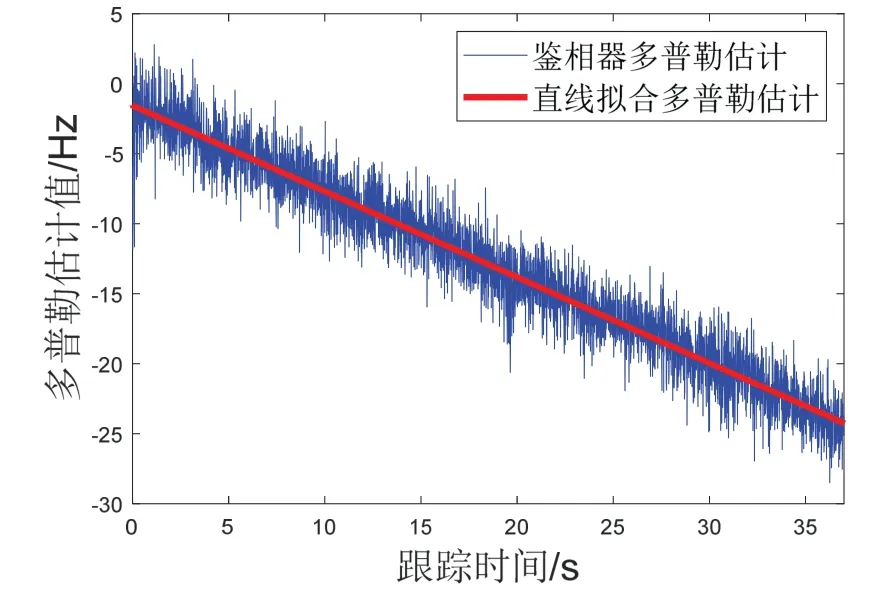
图8 多普勒直线拟合Fig.8 Doppler line fitting
根据该方法,获得精捕获前后各卫星信号多普勒频率误差,结果如表6所示。
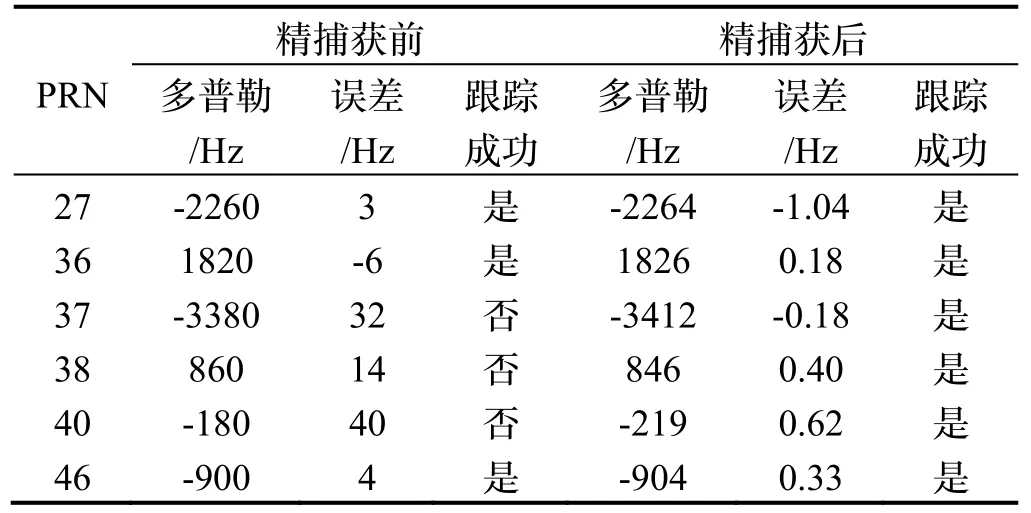
表6 快速精捕获算法精度对比表Tab.6 Precision comparison of fast fine acquisition algorithm
从表6 可以看出,当仅进行粗捕获时,频率搜索步长为80 Hz,以满足捕获最大步长要求,可以正确捕获对应的卫星信号,但由于捕获得到的多普勒误差范围相对较大,虽然满足捕获步长的最低要求,却无法确保跟踪环路的初值精度,发生跟踪失败的可能性较高;当使用本文提出的快速精捕获算法时,上述测试用例均实现了成功跟踪,且多普勒频率的捕获误差约0.46 Hz。
4 结论
本文针对北斗B1C 信号,在基于ASPeCT 算法消除副峰影响的基础上,设计了一种快速精捕获算法策略,该算法通过多级搜索和降采样策略实现了B1C 信号的快速捕获,大大减少了捕获过程中的FFT 计算量,并快速将频率估计缩小到一个较小范围,再结合多项式曲线拟合算法,实现了对多普勒的高精度捕获。经过真实信号测试,该快速精捕获算法将平均捕获时间相对缩短了近2/3,多普勒频率的平均估计误差在1Hz以内,保证了后续信号跟踪的成功率。

