波流耦合对漂浮式潮流能水轮机阵列影响的研究

饶 翔，路 宽，王花梅

（国家海洋技术中心，天津300112）

0 引言

作为开发利用海洋能源的重要装置，潮流能水轮机受到了广泛关注。潮流能水轮机的发电原理类似于风机发电，均是由流体带动流场，叶片捕获能量，带动发电机的转动进行发电。潮流能水轮机的研究最早借鉴于风机的研究成果，风机的尾流区域常常出现湍流、涡流等现象，这些因素会直接影响下游的风力机的发电效率，使得下游的风力机捕获能量减少，发电性能下降[1]，[2]。

基于风机的研究，许多学者对潮流能水轮机的水动力特性进行了研究。谭俊哲[3]对单桩潮流能水轮机进行了数值模拟分析，证明了潮流能水轮机振动位移时间序列的相似性。张玉全[4]提出了一种潮流能水轮机CFD致动盘数值模拟模型。有关潮流能水轮机阵列的研究，通常以水轮机的布局方式、波流荷载的影响与阵列的产能关系等因素为研究对象，并进行数值计算和实验[5]，[6]。黎江[7]对水平轴潮流能水轮机在正常工况与极限工况下的水动力特性进行了研究，研究发现：在正常工况下，水轮机的水动力性能波动很小；在极限工况下，波浪对水轮机叶片和支撑结构的强度影响较大。李林杰[8]通过调整潮流能水轮机组单排、多排之间的间距，找出最优的排布方式并进行数值分析与实验验证，最终得出了最优的水轮机布置方案。在传统潮流能水轮机研究的基础上，安琪[9]提出了潮流能水轮机阵列与海上锚泊浮台一体化的设计，并分析了浮台立柱扰流及不同排阵方案等因素对潮流能水轮机阵列抗干扰能力的影响。

固定式潮流能水轮机就是将桩基与水轮组合安装并固定在海底固壁的潮流能水轮机，这种潮流能水轮机的抗外荷载性能好，但是存在安装成本高、安装难度大、仅适用于较浅的水域以及桩基易受到海水腐蚀的问题。漂浮式潮流能水轮机须搭载载体平台，由浮子与锚系物约束其大范围运动，相比于固定式潮流能水轮机，漂浮式潮流能水轮机因底部基础不固定而特有摇荡特性，这使其始终处于受力不平衡，运动非定常的状态[10]。但是，漂浮式潮流能水轮机具有安装简单、易于移动和适应力强等特点，能在较深的海域工作。在IEC/TS 62600-200标准中，仅对固定式潮流能水轮机阵列的间距做出了规范，而对漂浮式潮流能水轮机阵列未作出明确要求。

目前，有关潮流能水轮机阵列的研究较少。因此，本文以固定式与漂浮式潮流能水轮机阵列为研究对象，对波流耦合作用下的不同结构型式的潮流能水轮机阵列的尾流场情况与能量利用效率进行研究分析。研究结果可为海上漂浮式潮流能水轮机阵列的间距设计、优化和安全性提供理论参考。

1 数值模拟理论

1.1 控制方程

流体运动受到物理守恒定律的支配，基本的守恒定律包括质量守恒定律、动量守恒定律与能量守恒定律，当流体处于湍流状态时，潮流能水轮机阵列的流动系统还要遵循附加湍流运输方程。其中，流体运动的质量守恒方程为

式中：ρ为海水密度；t为时间；xi为i方向的位移；ui为i方向的来流速度；Sm为分散的二级相中加入到连续相的质量。

水轮机在海水中工作，计算时可认为海水是密度均匀连续的不可压缩流体，且不存在分散的二级相，式（1）可简化为

在潮流能水轮机阵列流动系统中，微元体中流体流动的动量对时间的变化率等于外界作用在微元体上的各种力之和，潮流能水轮机阵列流动系统的动量方程为

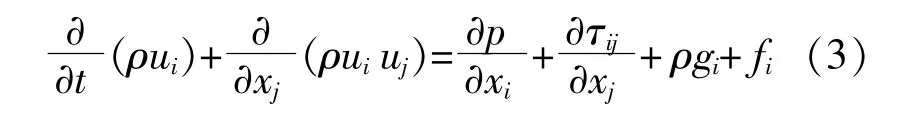
式中：p为压强；xj为j方向的位移；uj为j方向的速度；τij为切应变；gi和fi分别为i方向的重力体积力和外部波浪荷载作用的体积力。

由于海水比热容较大，在数值计算的时间内，海水温度不会有较大的变化，热交换很小可忽略不计，故能量守恒方程自动满足。

1.2 湍流模型

在实际海况中，潮流、波浪等因素作用在水轮机叶片时，叶片后方存在大小不一的涡旋。数值模拟中，选取合适的湍流模型可以有效降低计算量，提高计算精度。湍流模型数值计算方法见图1。

图1 湍流模型数值计算方法Fig.1Numericalsimulationmethod of turbulencemodel

涡粘模型的二方程包括standard k-ε模型、Realizable k-ε模型、RNG k-ε模型、standard k-ω模型和SST k-ω模型等。综合考虑数值计算的效率与精度、实际波流作用下的水轮机尾流的湍流强度大小与网格划分数量后，本文选取SST k-ω模型进行数值模拟，因为该模型的湍流粘度考虑到了湍流剪应力的传播，适用于复杂的几何边界的数值模拟流动[11]。SST k-ω模型中的湍流动能k方程与特殊耗散率ω方程为

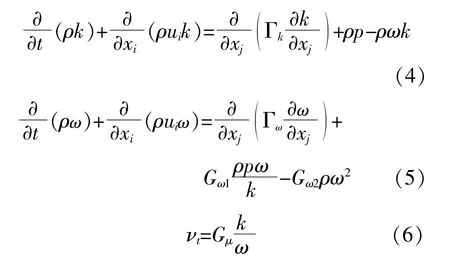
式中：Γk与Γω分别为k方程与ω方程中的有效扩散项；Gμ，Gω1和Gω2均为模型常量；νt为湍流运动粘性系数。

1.3 动网格技术

当水轮机自身旋转时，还会受到潮流力与波浪力的共同作用，波流耦合运动模型的数值计算不是一个简单的机械旋转问题，网格的运动须要适应外界因素的变化。当水轮机在波流耦合作用下产生运动，网格结点会产生位移，每次网格更新的结点位置与相邻结点保持拓扑学关系：

式中：ni为结点i相邻结点的个数；kij为第i个结点到第j个结点的迭代次数。在本文中，数值计算的精度默认为小于0.000 1时即满足需要。

2 数值计算

2.1 阵列布置

根据IEC/TS 62600-200标准中提出的固定式潮流能水轮机间距要求，建立了如图2所示的两种不同阵列。从图2可以看出：“田字”型阵列为前后并列布置的情况，包括4个完全相同的水轮机，3个前排水轮机的间距为2D（D为水轮机直径），后排的水轮机与前排中间的水轮机轴向对齐，间距为10D；“梅花”型阵列为前后交错布置的情况，包括5个完全相同的水轮机，3个前排水轮机的间距为2D，后排两个水轮机的间距也为2D，每个后排水轮机与其最近的前排相邻两个水轮机间距的中点对齐，间距为10D。

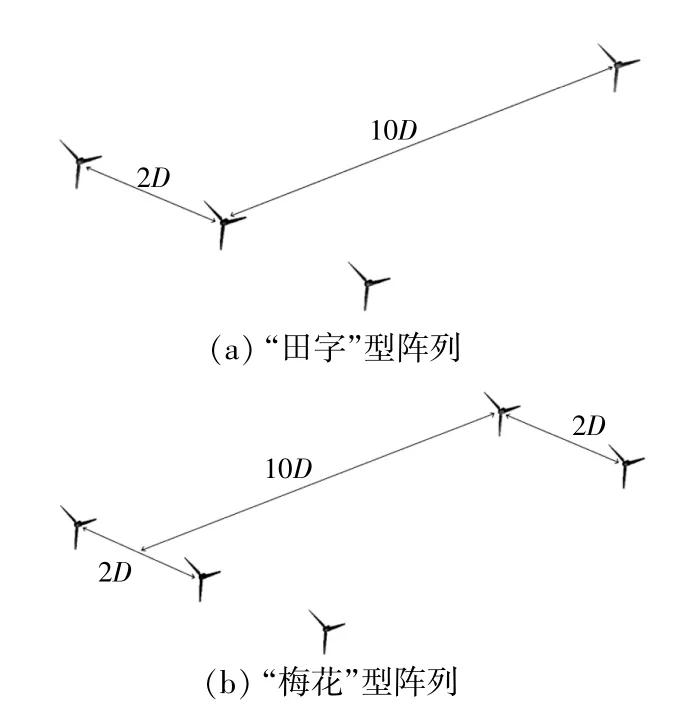
图2 潮流能水轮机阵列Fig.2 Array of tidal current turbines

2.2 数值模型

水平轴潮流能水轮机由轮毂与3个叶片构成，水轮机翼型采用NACA-0018翼型，叶片模型采用Solidworks建模，以坐标点的方式导入坐标数据进行合成。水轮机的直径D为2m，轮毂直径为0.1D，水轮机的三维模型如图3所示。

图3 水轮机模型Fig.3 Turbinemodel

波浪作用的运动响应通过漂浮式潮流能水轮机搭载的载体平台传递至水轮机上，为了体现水轮机的运动情况，对耦合运动的潮流能水轮机阵列数值模型做出简化，将载体平台受到波流作用时的响应作为水轮机的运动规律，以此建立水轮机阵列流场的数值模型。以“梅花”型阵列流场的数值模型（图4）为例，每个水轮机的旋转域为底半径为0.55D，高为0.2D的圆柱体，旋转中心距离总域的上、下边界均为3D；在流场中建立5个互相独立的球域，考虑水轮机受到波流作用时产生的最大位移，设置球域半径为0.95D，球心与水轮机旋转中心重合；总域是一个长为25D，宽为10D，高为6D的长方体。采用ICEM划分网格，球域与总域采用非结构化网格处理。水轮机叶片与轮毂采用结构化网格处理，考虑到水轮机叶片表面在流体中边界层的影响，其叶片表面第一层网格高度为0.02 cm，单个水轮机划分的总网格数为60万个。

图4 数值计算模型Fig.4 Numerical simulationmodel

2.3 边界条件

由于水轮机的运动是随时间不断变化的瞬态运动，所以在数值计算时采用瞬态求解的计算方法。在CFD中设置均匀潮流速度为2.5m/s，转速为48 rad/min，水轮机旋转3°为一个时间步长。出口边界相对大气压为0，其余壁面为滑移边界条件。水轮机的旋转发生在旋转域内，水轮机在波流耦合作用下产生的非定常运动发生在球域内，球域包含在总域内。每个旋转域与球域绕水轮机的旋转轴进行旋转运动，旋转域与球域网格的运动由不规则波的运动而给定，旋转域与球域、球域与总域之间均采用瞬态转子的交界面方式，以保证网格运动时网格质量不下降。

分析流场中的波流耦合问题时，须要额外增加波浪因素。由于CFD中没有波浪参数设置功能，须对其进行二次开发，通过用户自定义函数功能将波浪数据定义为wave函数，设置规则波的波高为0.2m，周期为2 s，波浪数据的划分频率为96 Hz。在流场数值计算时，水轮机总旋转数为30转，收敛条件为每个时间步长内的残差小于10-4。

3 结果分析

在数值计算结果中，前排水轮机的能量利用率对结果分析无影响，因此，本文不对其进行研究。为了研究后排水轮机及整体阵列的平均能量利用率的变化，记潮流能水轮机的能量利用率为Cp（无量纲），其计算式为

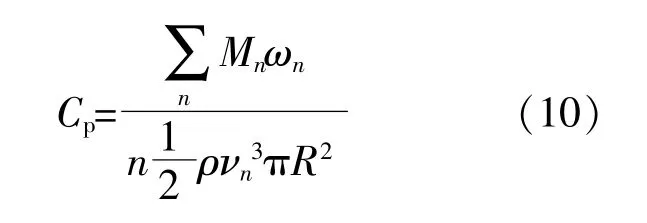
式中：n为第n个水轮机；ωn为水轮机的旋转角速度；Mn为水轮机的旋转力矩；R为水轮机的旋转半径；νn为潮流经过水轮机叶片时的速度。

3.1 能量利用率分析

3.1.1 “田字”型阵列的能量利用率

“田字”型阵列的能量利用率曲线如图5所示。从图5可以看出：当前排水轮机尾流经过后排水轮机时，后排的固定式水轮机的能量利用率下降了1.5%，能够获取降低前能量的94.6%；后排的漂浮式水轮机的能量利用率下降了3.5%，只获取了降低前能量的88.3%。由于后排的漂浮式水轮机的能量利用率下降较快，且漂浮式阵列的能量利用率曲线的波动幅度大于固定式阵列的能量利用率曲线。因此，在“田字”型阵列中，当漂浮式与固定式水轮机的布置间距相同时，后排的漂浮式水轮机的能量利用率曲线波动较大，即漂浮式水轮机不适用于“田字”型阵列的实际海上工程。

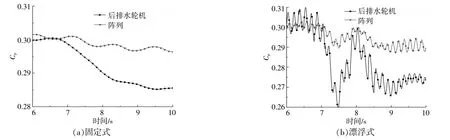
图5 “田字”型阵列的能量利用率曲线Fig.5 Power conversion efficiency curves of"Tian Zi"type array

3.1.2 “梅花”型阵列的能量利用率

“梅花”型阵列的能量利用率曲线如图6所示。从图6可以看出：关于流场左右对称的两个后排水轮机的能量利用率曲线的变化规律基本一致。在固定式的“梅花”型阵列中，受到前排水轮机尾流影响后，后排水轮机的平均能量利用率增大了0.5%，阵列的单个水轮机与阵列的平均能量利用率未大幅下降，能达到降低前能量的99.2%，由此可见，在固定式的“梅花”型阵列中，前排水轮机尾流对后排水轮机的影响很小。在漂浮式的“梅花”型阵列中，后排水轮机的平均能量利用率下降了1.4%，在一个旋转周期内，水轮机的能量利用率最值仅相差1.2%，能够获取降低前能量的95.6%。综上可以看出，在“梅花”型阵列中，漂浮式水轮机的能量利用率小于固定式水轮机。

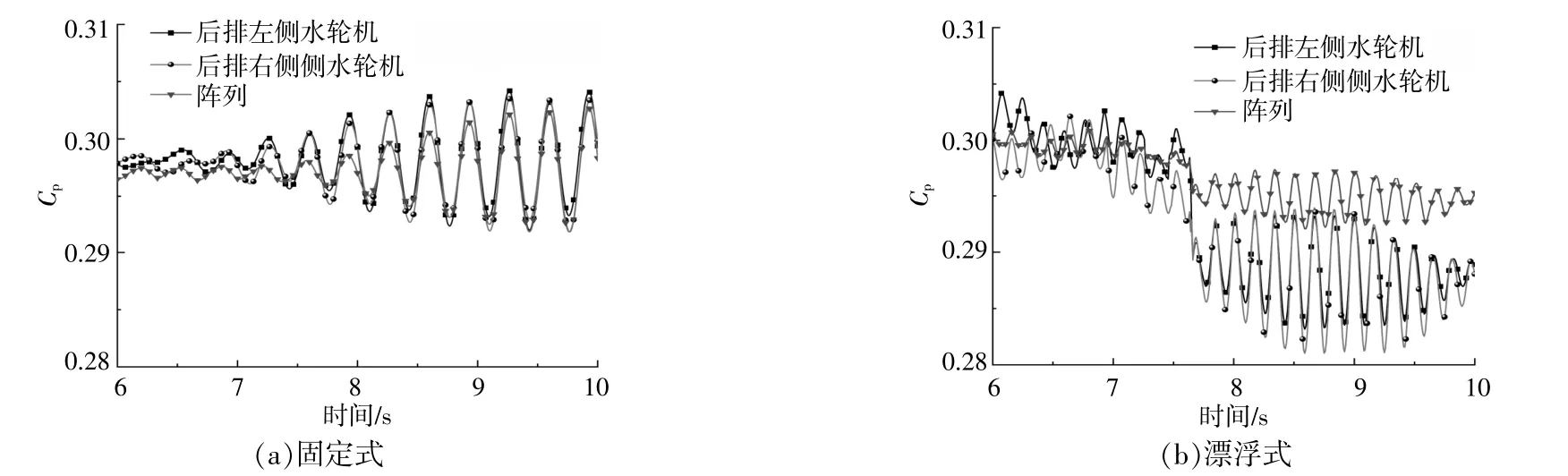
图6 “梅花”型阵列的能量利用率曲线Fig.6 Power conversion efficiency curves of"Plum Blossom"type array

随着前排水轮机的尾流经过后排水轮机之后，后排水轮机的能量利用率受到了不同程度的影响。当后排水轮机在波流耦合作用下发生旋转及摇荡时，总体而言，“田字”型阵列的整体能量利用率曲线的波动幅度大于“梅花”型阵列。

3.2 尾流场分析

为了进一步分析水轮机在波流耦合作用下的荷载波动机理，选取尾流场稳定后的最后一个周期来分析水轮机阵列尾流场的变化情况。

3.2.1 “田字”型阵列的尾流场

水轮机在“田字”型阵列的尾流场速度分布如图7所示。从图7可以看出：在固定式的“田字”型阵列中，前排中间的水轮机的尾流对后排水轮机的影响最大，后排水轮机正好处于前排中间的水轮机的狭长低速尾流内，两侧水轮机的尾流对后排水轮机几乎没有影响；在漂浮式的“田字”型阵列中，水轮机尾流两侧分别产生涡旋，后排水轮机的尾流低速区域增大，这是由于水轮机在自身旋转的同时，还受到的波流耦合荷载的作用。

图7 “田字”型阵列的尾流场Fig.7Wake flow flied in"Tian Zi"type array

3.2.2 “梅花”型阵列的尾流场

水轮机在“梅花”型阵列的尾流场速度分布如图8所示。从图8可以看出：在固定式的“梅花”型阵列中，前排水轮机尾流的低速区主要存在于水轮机旋转平面至后方3D之间，直到10D处才逐渐恢复至初始流场速度；而在漂浮式的“梅花”型阵列中，后排水轮机吸收了前排3个水轮机的大部分低速尾流，由于尾流效应与阻塞效应的影响，前排水轮机的低速尾流增大了后排水轮机的低速尾流面积。

图8 “梅花”型阵列尾流场Fig.8Wake flow flied in"Plum Blossom"type array

4 结论

本文通过流体力学CFD软件对波流耦合作用下的潮流能水轮机阵列进行数值模拟与分析，得到了如下结论。

①在“田字”型阵中，由于水轮机的布置方式为并列布置，前排水轮机的尾流会严重影响后排水轮机的流场，导致后排水轮机的能量利用率明显降低。

②在“梅花”型阵列中，相比于漂浮式水轮机，固定式水轮机的前排尾流对后排水轮机的影响更小，后排水轮机的能量利用率更稳定。

③在前后排水轮机间距为10D的情况下，漂浮式水轮机的前排尾流对后排水轮机的影响程度较大，在实际海上工程中，应适当增加前后排水轮机的间距。