基于图像特征的卷积核初始化方法

李鹏松, 李俊达, 倪天宇, 张 琦, 胡建平

(东北电力大学 理学院, 吉林 吉林 132012)

卷积神经网络(convolutional neural network, CNN)是计算机视觉领域中的重要模型, 由卷积层、 池化层和全连接层构成, 其参数量巨大[1]. 近年来, 为进一步提高其性能和应用范围, 研究者们从网络结构、 损失函数和优化算法等方面对卷积神经网络进行了各种改进[2-6]. 在改进过程中卷积神经网络的深度不断增加[7-9], 而卷积核作为其中数量最多的参数, 对网络性能的影响逐渐增大. 庞大的卷积核数量也使卷积核的更新状况与其初始值紧密相连, 因此卷积核的初始化对网络的识别性能和收敛速度起决定作用. 由于卷积神经网络中参数多、 网络结构复杂, 因此卷积核的初始化方法主要以随机初始化为主, 即根据某特定的概率分布生成一组随机数作为卷积核的初始值. 但大多数卷积神经网络的深度较深, 随机初始化会使网络中卷积层输出值的方差越来越大, 最终导致网络收敛速度变慢[10]. 针对上述问题, Glorot等[11]提出了Xavier初始化方法, 通过使各卷积层输入输出值的方差一致防止网络在前向传播时累积方差, 但该方法成立的前提是网络的激活函数为对称函数, 而大多数卷积神经网络的激活函数是非对称函数, 因此并不适合卷积神经网络； Krizhevsky等[12]在提出AlexNet的同时, 使用Gauss初始化方法初始化卷积神经网络, 该方法通过Gauss分布使卷积层输出值的期望为零, 同时通过设置极小方差限制各卷积层输出值的方差, 从而降低网络不收敛的可能性, 该方法简单有效, 但随着网络深度的加深, 方差仍会不断累积; He等[13]以Xavier初始化方法为基础提出了He初始化方法, 该方法可适应不同类型的激活函数, 更适合初始化卷积神经网络. 上述方法均基于随机初始化, 其局限为： 1) 随机初始化方法存在较大的偶然性和不确定性, 导致增加网络的不稳定性, 进而导致网络收敛速度较慢; 2) 在初始化过程中只考虑了输出值的方差, 并未考虑数据集自身的特征, 从而限制了网络的识别性能.

马义超等[14]建立了基于主成分分析(principal component analysis, PCA)初始化的卷积神经网络模型, 该模型提取图像模板的主成分, 并将其作为卷积核的初始值, PCA算法虽然可以构建网络并初始化卷积核, 但却无法作为一种普遍适用的初始化方法, 其原因是： 1) 使用PCA算法提取的特征向量数量应小于其对应方阵的阶数, 即PCA算法可初始化的卷积核数量不能超过单个卷积核所对应的神经元个数, 但大多数卷积神经网络的卷积核数量远大于单个卷积核所对应的神经元个数, 因此PCA算法只能初始化极少数特定结构的网络; 2) PCA算法未考虑到卷积层输出值的方差, 当卷积核的数量较多时, 卷积层输出值的方差会显著增加, 进而降低网络收敛的可能性.

针对上述问题, 本文提出一种基于图像特征的卷积核初始化方法, 既保留了PCA算法可使网络训练结合图像特征的优点, 又解决了PCA算法无法初始化任意网络结构的问题. 本文首先使用图像处理技术突显图像特征; 然后使用PCA算法初始化首层卷积核; 最后对卷积层的特征图进行随机组合, 并分别使用PCA算法和特征截断完成各卷积层的初始化. 本文初始化方法使用图像处理技术和PCA算法使卷积神经网络的训练结合不同类型的图像特征, 进一步增强了网络的特征提取能力； 使用特征截断进一步限制卷积层输出值的方差, 使其可适应卷积核数量较大的网络, 并进一步增加网络的稳定性； 将随机组合应用于卷积核初始化, 解决了PCA算法受网络结构限制的问题.

1 主要结果

本文初始化方法分为3个阶段： 第一阶段是模板集构建阶段, 从训练集中选取图像模板并通过图像处理技术构建纹理、 颜色和边缘模板集； 第二阶段是首层卷积核初始化阶段, 使用PCA算法提取主成分并将截断后的主成分作为首层卷积核的初始值； 第三阶段为其他层卷积核初始化阶段, 计算每个卷积层的特征图并进行随机分组, 再分别通过PCA算法和特征截断初始化其他卷积层. 本文初始化方法流程如图1所示.

1.1 模板集构建

根据文献[11-12]对卷积核的定性分析可知, 卷积核所提取的抽象特征主要基于图像中的简单边缘及模糊的颜色分布. 因此, 颜色与边缘特征对初始化卷积核具有重要作用. 本文构建颜色模板集与边缘模板集, 并且为防止具体颜色与边缘特征降低网络的泛化能力, 本文根据原始图像构建纹理模板集作为对图像特征的补充. 模板集效果如图2所示.

1.1.1 构建纹理特征模板集

由于纹理特征较抽象, 盲目使用图像处理技术会降低卷积神经网络的泛化能力, 因此, 本文将原始图像作为提取图像纹理特征的模板, 步骤如下.

图1 本文初始化方法流程

1.1.2 构建颜色特征模板集

使用均值滤波器对图像进行模糊处理, 只保留图像大致的颜色分布. 本文以模糊化图像作为提取图像颜色特征的模板, 步骤如下.

1) 建立滤波器尺度15的均值滤波器:

2) 平滑处理: 根据

(1)

得模糊化图像数据集G1={G11,G12,…,G1N}, 其中G1i为第i个模糊化的图像样本,i∈{1,2,…,N},N为图像样本数量.

1.1.3 构建边缘特征模板集

边缘检测技术可在保留图像结构的情况下, 去除图像大量不相关的信息[15]. 本文使用Sobel算子对图像进行边缘处理, 将保留的图像边缘作为提取图像边缘特征的模板, 步骤如下.

1) 建立Sobel算子:

2) 边缘处理:

|G2i|=|G2i,x|+|G2i,y|,

(4)

根据式(2)和式(3)进行边缘处理得到边缘特征集G2={G21,G22,…,G2N}， 其中G2i为第i个边缘处理后得到图像样本,i∈{1,2,…,N}.

1.2 初始化首层卷积核

PCA算法的学习结果与隐层神经元数量受限时的多层感知机学习结果相似性高, 可与神经网络进行结合[16]. 因此, 本文使用PCA算法提取模板集的主成分, 并将其应用于卷积核初始化. 由于直接使用主成分作为卷积层的初始值通常会使卷积层输出值的方差明显增加, 因此本文采用特征截断以控制卷积层输出值的方差.

1.2.1 PCA算法提取主成分

(5)

1.2.2 特征截断

本文对主成分进行截断, 将对方差影响较大的异常数据进行替换, 避免输出值出现方差过大的情形. 特征截断公式为

(6)

1.3 初始化各层卷积核

1.3.1 特征图计算

在已知卷积核初始值的情况下, 通过卷积计算得到其他卷积层所输出的特征图[17], 计算公式为

(7)

1.3.2 PCA算法提取特征向量

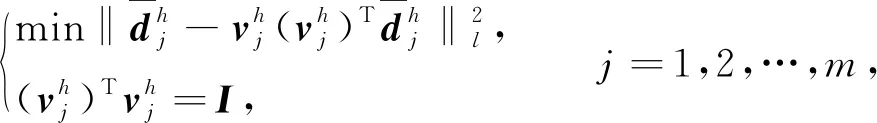
(8)

2 实验测试

本文在Intel Core i5-4210M 2.6 GHz CPU, 内存为8 GB的Windows 8.1系统上使用框架tensorflow 1.5进行实验测试.

2.1 实验方法

使用基于图像特征的卷积核初始化方法确定卷积神经网络的初始权重, 将网络应用于数据集Cifar-10和Corel-1000的识别任务中, 并与其他卷积核初始化方法进行对比. 将实验数据分为训练集、 验证集和测试集, 其中: 训练集与验证集参与训练过程, 训练集训练模型, 验证集确定模型超参数； 测试集测试网络的识别性能. 所用数据集信息列于表1. 用于测试初始化效果的模型为有三层卷积结构的卷积神经网络, 其结构如图3所示.

表1 数据集信息

由于数据集Corel-1000的数据量较小, 使用大量卷积核会导致网络出现严重的过拟合现象, 进而影响对初始化效果的评价. 因此, 用于识别数据集Corel-1000的卷积神经网络的卷积核个数较少, 各层卷积核个数为16,32,64； 用于识别数据集Cifar-10的网络各层卷积核个数为32,64,128.

图3 卷积神经网络结构示意图

2.2 结果分析

本文从网络的收敛程度、 泛化能力和初始化成本三方面评价初始化方法. 使用验证集的损失值衡量网络的收敛程度, 使用测试集上的识别准确率衡量网络的泛化能力, 使用训练时间衡量初始化成本. 利用验证集的损失值收敛程度分析不同初始化方法对卷积神经网络收敛速度的影响, 结果如图4所示.

图4 不同初始化方法的验证集损失值对比

由图4(A)可见, 在数据集Cifar-10上使用Gauss初始化的网络约在2 000次迭代时收敛, 使用He初始化的网络约在3 100次迭代时收敛, 本文方法初始化后的网络约在1 400次迭代时收敛, 其收敛速度大于其他两种初始化方法. 对比3种方法在Cifar-10任务中的表现： 本文初始化方法的损失值始终小于其他两种方法, 在0～1 500次迭代时损失值差距明显; 在3 000次迭代后, 各方法损失值之间的差距逐渐稳定, 不再出现明显变化； 本文初始化方法的损失值收敛于0.010, 其他两种方法的损失值分别收敛于0.040和0.039. 由图4(B)可见, 使用Gauss初始化的网络在180次时收敛, 使用He初始化的网络在200次迭代时收敛, 本文方法初始化后的网络在150次时收敛, 其收敛速度仍快于其他两种初始化方法. 对比3种方法在Corel-1000任务中的表现： 本文方法的损失值在150次迭代前与其他两种方法之间并无明显差异, 但在150次迭代后, 本文方法开始收敛并且损失值始终低于其他两种方法; 本文方法的损失值收敛于0.019, Gauss初始化方法的损失值收敛于0.031, He初始化方法的损失值收敛于0.051. 实验结果表明, 在不同任务中, 使用本文方法初始化的网络均具有更快的收敛速度和更小的损失值, 验证了本文初始化方法的优越性.

为进一步评价本文初始化方法的性能, 对比不同初始化方法对卷积神经网络泛化能力的影响, 结果列于表2.

表2 不同初始化方法的测试集识别准确率(%)对比

由表2可见, 本文初始化方法在两个任务中的识别准确率均超过94%, 且与人眼的识别准确率(94.9%)相近, 进一步说明了本文方法的实际应用价值.

对比3种初始化方法在Cifar-10任务中的表现： 使用本文初始化方法的网络在测试集上的识别准确率分别比使用Gauss初始化和He初始化的网络高2.0%和3.1%. 对比3种初始化方法在Corel-1000任务中的表现： 使用本文初始化方法的网络识别准确率分别比Gauss初始化和He初始化后的网络高8.5%和3.0%. 实验结果表明, 本文方法在不同识别任务中其识别效果均优于其他初始化方法, 进一步验证了本文方法的优越性. 对比3种初始化方法在不同任务中的识别差异： 本文初始化方法在不同的识别任务中, 其识别准确率只相差0.5%, 而其他两种方法则分别为4.0%和0.6%, 说明使用图像特征可使网络更好地适应不同类型的数据集, 验证了本文初始化方法的合理性. 实验结果表明, 本文初始化方法与其他初始化方法相比, 可使网络具有更好的识别性能, 并且对不同任务的适应性也更好.

为评价本文初始化方法的实用性, 利用训练时间量化初始化成本, 结果列于表3. 由表3可见, Gauss初始化与He初始化并不会对网络训练产生额外的时间, 而本文方法需要耗费一定时间才能完成对网络的初始化. 对比其他两种方法： 本文初始方法在Cifar-10和Corel-1000任务中的平均训练时间分别增加0.3%和4.9%, 均小于5%. 因此, 本文初始化方法并没有增加大量的网络训练时间, 具有一定的实际应用价值. 对比本文方法在两个任务中的表现： Corel-1000任务远大于Cifar-10任务中的初始化时间, 这是由于数据集Cifar-10中的图像尺寸更小, 特征提取更快. 因此, 本文初始化方法更适用于图像尺寸较小的图像识别任务.

表3 不同初始化方法的训练时间(s)对比

综上所述, 本文以图像处理技术与PCA算法为基础, 提出了一种基于图像特征的卷积核初始化方法. 首先, 提取图像的纹理、 边缘和颜色特征构建特征模板集； 其次, 使用PCA算法提取图像特征的主成分完成首层卷积核初始化; 最后, 计算各卷积层输出的特征图, 并再次提取主成分, 逐层完成卷积核初始化. 实验结果表明, 本文初始化方法的初始化成本较少, 识别性能更优越, 对不同类型的任务都具有较好的适应性, 有实际应用价值.