基于Bi-LSTM/Bi-GRU循环神经网络的锂电池SOC估计

朱元富，贺文武，李建兴，李有财，李培强

（1福建工程学院，福建 福州350018；2福建星云电子股份有限公司，福建 福州350015）

为有效缓解温室效应等引发的全球变暖以及化石能源的过度使用而造成的环境污染等问题，全球能源的使用结构正在发生积极改变。传统化石能源的使用比例逐渐下降，新型可再生能源的使用比例则逐渐上升[1]。锂电池因其循环寿命长、能量转换效率高、比能量大、充电效率快、自放电率低等优点，在能源市场占用率不断攀升，已然成为储能元件的首选[2]。快速成长的电动汽车等领域更是高度依赖于锂电池等相关技术的发展。

电池的SOC 具体定义为电池的剩余容量与其标称容量的比例[3]，是能量管理与控制的主要依据。SOC 不仅为电池的使用性能提供参考信息，同时也是电池组电池管理系统的重要基础，对电池的保护、工作效率以及使用寿命等具有重要的指导作用。锂电池荷电状态物理上具有高度复杂的非线性特性，一般难以直接测量。因此，准确估计电池的SOC 对电池的高效利用以及电动汽车的整车能量管理等具有重要意义[4]。当前电池SOC的主要估计方法可分为如下几大类型。

一是基于电池性能参数的估计，即通过测量电池的电流、电压或电池内阻等进行估计，其典型方法有安时积分法[5]，开路电压法(OCV)[6]以及内阻法[7]等。一般来说，安时积分法需要获取初始的SOC 值，同时因电流传感器的噪声影响，SOC 相关测量值会产生偏移，并随时间递增而导致误差累积。相较安时积分法，开路电压法的SOC 相关测量值更接近于真实值，但被测电池需要长时间静置，以获得平衡后的OCV-SOC曲线，较长的时间代价使得该方法难以在实践中大规模使用。基于内阻的估计法，其适配通用性较弱，易受到电池类型、数量以及电池间的一致性等因素影响，应用相对局限，较少用于电动汽车领域。

二是基于模型的估计，即通过等效电路模型或电化学模型进行SOC 估计，常见的方法有卡尔曼滤波器(KF)[8-10]、粒子滤波器[11]与自适应观测器[12]等。文献[8]根据电池的状态空间方程并结合扩展卡尔曼滤波算法来估计电动汽车锂电池的SOC。因KF算法的抗干扰能力强，其估计结果具有较高鲁棒性，适用于相对复杂环境下的SOC 估计。文献[9]与文献[10]则基于KF算法，在滤波方法与参数模型上进行改进以提升其SOC 估计性能。实际应用中，由于锂电池的状态空间高度非线性，基于KF 算法的SOC 估计方法复杂度高，计算量大。为提升SOC的估计效率与精度，文献[11]与文献[12]则分别以粒子滤波器与自适应观测器来替代卡尔曼滤波，在一定程度上降低了算法复杂度，减少了计算量。不难理解，基于模型的SOC 估计方法的精度直接依赖于电池模型的准确性，而准确构造电池模型、估计相关模型参数本身在实际应用中具有高度的挑战性。

三是基于数据驱动的估计，即通过机器学习技术，如支持向量机[13]与神经网络[14-16]等方法从数据驱动角度对电池SOC进行估计。文献[13]将最小二乘支持向量机结合分布估计算法应用到锂电池SOC的估计中，并在仿真实验中验证了其有效性。神经网络，特别是深度神经网络具有高精度的通用逼近能力，适用于复杂非线性系统的建模，被广泛应用于工程领域，近年来也逐渐成为估计电池SOC 的主流方法。通过对电池电压、电流、温度以及内阻值的实时测量，文献[14]基于反向传播神经网络有效降低SOC的估计误差。文献[15]将循环神经网络中的长短期记忆网络用于SOC 估计，能对数据相关性进行编码实现SOC 的准确估计。自然地，结合数据驱动与电池模型方法则有望进一步提升SOC的估计性能。基于此，文献[16]将前馈神经网络与EKF算法相结合，估计复杂工况下的电池SOC，其实验结果表明其估计误差可以稳定在2%以内。然而，前述基于数据驱动的“浅模型”估计方法虽能一定程度上有效拟合非线性性，但难以有效捕捉电池在物理或电化学特性时间维度上的动态特性，而直接引入深层神经网络则易产生梯度消失或爆炸等问题，因此需要探索更为有效的基于数据驱动的SOC估计方法。

针对SOC 估计中所涉相关物理或化学特性时间维度上的长程依赖问题，本文基于循环神经网络(RNN)，引入双向学习策略，有效表征电池内部的动态物理特性，并具体构造基于双向循环神经网络Bi-LSTM/Bi-GRU的SOC估计模型。相关模型将在基准数据集上进行充分实验，验证其有效性，并与现行相关算法进行深入比较。

1 循环神经网络

1.1 经典循环神经网络RNN

循环神经网络起源于20 世纪90 年代[17]。与输入、输出只取决于当前时刻参量的一般神经网络不同，RNN 能处理变长序列数据，其当前时刻状态不仅取决于当前时刻的输入，同时也取决于先前时刻的网络状态。RNN 通过递归单元来存储历史信息，其标准模型及其展开结构如图1所示。其基本计算流程为： 输入端输入序列数据X =(x1,...,xt-1,xt)，经式(1)计算得到状态序列H =(h1,...,ht-1,ht)，经式(2)计算得到输出端输出序列

Y =(y1,...,yt-1,yt)。

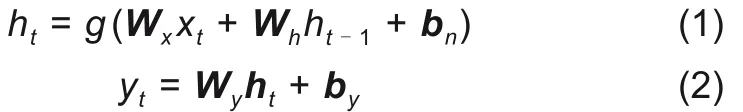
式中，g(⋅)表示RNN 网络的激活函数；W 表示不同层之间传递的权重矩阵(如Wy是隐藏层h到输出层y的权重矩阵)；b表示不同层中的偏置向量(如by为输出层y的偏置向量)。

图1 RNN的标准结构与展开结构Fig.1 The standard structure and unfolded structure of RNN

RNN 的特殊结构使其能够通过存储、记忆及其对先前一段序列数据的处理实现序列预测，能有效处理非线性序列预测问题。实际应用中，经典RNN 存在长程依赖问题，即随序列延长以及隐藏层复杂度的加深，其梯度在反向传播过程中会变得很大或很小，出现梯度爆炸或梯度消失现象，从而难以建立长距离依赖关系的有效模型。因此，相关研究者转向更为有效的长程模型。

1.2 长短期记忆网络LSTM

为消解RNN 存在的梯度爆炸或消失问题，Hochreiter 与Schmidhuber 引入门控机制，提出长短期记忆(LSTM)的网络结构[18]，以LSTM的循环单元结构取代经典RNN 的状态单元。经典RNN 中，隐状态“记忆”历史信息，但每个时刻的隐状态都会被重写，从而只能是一种短期记忆。LSTM则因其专门构造的记忆单元能有效捕捉关键信息并保持一段较长时间，但短于长期记忆(神经网络中，长期记可视为网络参数，其更新周期远慢于短期记忆)，从而形成一种长的短期记忆。

LSTM的循环单元包含三种门控结构，分别为遗忘门ft、输入门it以及输出门ot。三种门均采用Sigmoid 激活函数对输入信息及隐藏层状态进行处理。Sigmoid函数能将信息有效控制在[0,1]范围内。Sigmoid输出为1表示所有信息通过，Sigmoid输出为0则表示门限关闭从而无信息可以通过。具体地，遗忘门控制历史信息的遗忘程度，输入门控制当前输入信息(候选状态)的记忆程度(多少信息被保存)，输出门则控制当前网络内部状态输出给外部状态的程度。得益于门控机制，LSTM网络能动态调适历史信息的存储与遗忘并控制梯度尺度，合理设置门控初始参数的条件下能有效消解梯度爆炸或消失问题。LSTM循环神经网络的具体结构如图2所示。

LSTM 网络循环单元的计算流程为：以t 时刻的输入xt、t - 1时刻的隐藏层状态ht-1为输入，通过式(3)～(5)更新三个门控，通过式(6)更新内部状态ct，并最终通过式(7)更新隐藏层状态ht。

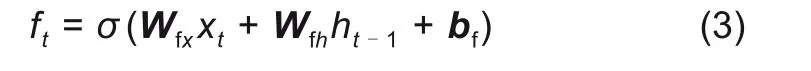
式中：ft、it、ot、ct、ht分别表示遗忘门输出、输入门输出、输出门输出、内部状态、隐藏层状态；σ、tanh 分别表示Sigmoid 激活函数与双曲正切函数;Wfx、Wfh、Wix、Wih、Wox、Woh、Wcx、Wch为对应部件的权重矩阵；bf、bi、bo、bc为对应部件的偏置向量。

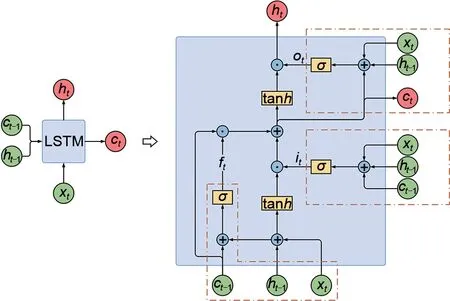
图2 LSTM网络的循环单元结构Fig.2 The structure of LSTM network

1.3 门控循环单元GRU

LSTM网络的发展催生了诸多网络变体，典型的如当前流行的门控循环单元(GRU)网络[19]。GRU与LSTM 性能相近[20]，能有效处理梯度消失或爆炸问题、捕获长程依赖关系，同时其结构简单、计算效率高、网络参数少、存储空间小。GRU 只有两个门控结构，其一是将LSTM中的遗忘门与输入门合并成更新门zt，用于控制输入与遗忘之间的平衡；另一个是重置门rt，用于控制对前一时刻状态信息的依赖程度，其值越小表示依赖程度越低。GRU网络循环单元的具体结构如图3所示。

GRU网络循环单元的计算流程为：以t时刻的输入向量xt与t - 1时刻的隐藏层状态ht-1为输入，通过式(8)～(9)更新重置门与更新门的输出zt与rt，通过公式(10)更新候选状态h't，并最终通过式(11)更新隐藏层状态ht。

式中，Wrx、Wrh、Wzx、Wzh、Whx、Whr表示对应于更新门、重置门以及隐藏层等的权重矩阵，br、bz、bh表示相应部件的偏置向量。

图3 GRU网络的循环单元结构Fig.3 The structure of GRU network

1.4 双向循环神经网络Bi-LSTM/Bi-GRU

LSTM 网络或GRU 网络能有效处理变长序列的长程依赖问题，在自然语言处理、时间序列分析及其他涉及序列数据处理的领域得到广泛应用，但是，前述网络仅单向考虑序列间的关联，未考虑未来信息的可能关联，在往返关联性较强的应用上有较大局限。SOC 估计的实际应用中，如仅单向考虑电池的观测数据与相应SOC 间的关联，可能不足以捕捉电池物理或电化学上的动态特性，即一个时点上的SOC 值与该时点前后电池的观测数据应该具有强关联。因此，我们需要整体考虑电池的序列观测数据，在正向关联序列的基础上引入逆序关联，以提升SOC的估计性能。

针对上述序列关联问题，Graves等[21]提出了双向长短期记忆(Bi-LSTM)循环神经网络。相应地，将其思想迁移至GRU 网络，即可得到双向门控循环单元(Bi-GRU)网络[22]。双向循环神经网络基于序列整体预测输出，具有利用序列数据上下文所含信息进行学习的能力，具体到SOC 估计问题上，即可利用待估计SOC 值相应时点前后的电池观测数据来进行估计。Bi-LSTM/Bi-GRU 网络包含正、反向两个LSTM/GRU 层，正向传播的LSTM/GRU 用来计算当前时刻的序列信息，反向传播的LSTM/GRU 则逆向读取同一序列，引入逆序信息。两个LSTM/GRU 网络层共同连接一个输出层，在网络训练过程中为输出层中的所有神经元提供正向与逆序两类信息。Bi-LSTM/Bi-GRU 网络的具体结构如图4所示。

图4 Bi-LSTM/Bi-GRU的网络结构Fig.4 The structure of Bi-LSTM/Bi-GRU network

由图4可知，双向循环网络的主体结构就是两个单向循环网络的组合。它们的输入相同，信息的传递方向相反，两者结构对称。两个网络具体通过式(12)与(13)独立进行计算、无交互，各自更新状态、产生输出，并最终根据式(14)拼接两个方向上的输出。

式中，h't、ht、xt、Ht表示t 时刻的正向传播隐藏层状态、反向传播隐藏层状态、输入神经元的输入值、隐藏层状态的输出值；f 表示隐藏层的激活函数；W1、W2、W3、W4表示不同部件对应的权重矩阵；h't-1、ht+1表示t - 1时刻的正向传播隐藏层状态、t + 1时刻的反向传播隐藏层状态；b't、bt表示正向传播隐藏层、反向传播隐藏层的偏置向量；⊕为向量拼接操作。

2 基于双向循环神经网络的锂电池SOC估计模型

2.1 特征选取

电动汽车实际驾驶过程中的行驶工况通常比较复杂，同时伴随多种影响电池性能的不确定因素，因此在构建电池SOC 估计模型前需要对输入特征进行必要的分析与提取。输入特征一方面要能较好地反映锂电池不同工况下的实际状态，同时输入特征本身在实际条件下应该易于获取。电池特性相关参数繁多，包括电压、电流、温度、内阻、电解液溶度等。其中，内阻、电解液浓度等参数的观测通常需要借助大型精密仪器设备才能较为准确地测量，且被观测电池需要长时间静置，整个观测过程周期较长，在实际的SOC 估计环境中并不通用。与之不同，诸如电压、电流、温度等电池特性参数，则能通过相对简易的方法快速测量，在保证较为准确测量的同时还能直接表征锂电池某时段上的工作状态，从而能在SOC 估计中起到重要作用。因此，本文构建的基于双向循环神经网络的锂电池SOC 估计模型以电池的工作电压、电流以及温度作为输入特征，使得估计模型更接近真实的使用工况，以期提升模型的估计性能。

2.2 模型构建

本文构建的基于双向循环神经网络Bi-LSTM/Bi-GRU的锂电池SOC估计模型主要由输入层、隐藏层和输出层组成。输入层输入选取的电池特性序列，此处为电池不同时点的电压、电流与温度；隐藏层包含Bi-LSTM/Bi-GRU层与全连接层，主要学习、表征电池特性序列与SOC 序列之间的内在关联；输出层输出模型的估计值。本文所构建的估计模型具体如图5所示。

图5 基于Bi-LSTM/Bi-GRU的锂电池SOC估计模型Fig.5 The model of SOC estimation for Lithium-ion battery based on Bi-LSTM/Bi-GRU

完整的SOC 估计过程还包括输入特征选取、数据标准化、数据集划分等。模型的输入是时间步长为τ 的电池端电压Vτ、电流Iτ以及温度Tτ构成的电池特性观测序列，模型的输出是时间步长τ 的SOC 估 计 序 列SOCτ。h'τ(1),h'τ(2),...,h'τ(n)为模型正向传播的隐藏层神经元节点，hτ(1),hτ(2),...,hτ(n)为模型反向传播的隐藏层神经元节点，n 代表隐藏层神经元节点个数。同一Bi-LSTM/Bi-GRU 网络中，正向传播与反向传播的隐藏层神经元节点个数相同。

为方便理解，将Bi-LSTM/Bi-GRU 网络按时间步长τ展开，所得模型结构如图6所示。对于第k个隐藏层神经元节点，将序列电池特性观测数据[Vτ,Iτ,Tτ]按时间步长展开为[V1,I1,T1],...,[Vτ-1,Iτ-1,Tτ-1],[Vτ,Iτ,Tτ]，以此为输入层的输入，输出层的输出则是τ 时刻的模型估计值SOCτ，即包括当前时刻的长度为τ 的SOC 序列[SOC1],...,[SOCτ-1],[SOCτ]，其 余 隐藏层神经元节点依此类推。

图6 单个隐藏层神经元节点按时间步长展开图Fig.6 The unfolded structure of a neuron in hidden layer

基于双向循环神经网络Bi-LSTM/Bi-GRU 的锂电池SOC估计方法的具体流程如下所述。

步骤I：数据预处理。选择适当的网络模型输入特征，对数据进行标准化处理，并将数据划分为训练集与验证集；

步骤II：设定Bi-LSTM/Bi-GRU 网络模型的基本结构。设定输入层、隐藏层以及输出层的神经元节点个数，选择适当的激活函数、损失函数以及自适应优化器等；

步骤III：设置Bi-LSTM/Bi-GRU 网络的超参数。设置时间步长、迭代次数、采样间隔以及训练批量大小等，同时对权重矩阵与偏置向量进行初始化。

步骤IV：训练网络模型。基于训练集数据训练Bi-LSTM/Bi-GRU 网络，迭代优化网络模型参数，直到满足前述相关设定条件；

步骤V：测试网络模型。基于验证集数据测试步骤IV训练好的Bi-LSTM/Bi-GRU网络，选择适当的评价函数，验证Bi-LSTM/Bi-GRU 网络模型的SOC估计性能。

3 锂电池数据集

3.1 Panasonic 18650PF锂电池数据

本文实验采用Panasonic 18650PF 锂电池数据集[23]，该数据由加拿大马克马斯特大学自动化所收集。数据集中，锂电池的额定电压为3.6 V、额定容量为2.9 A·h，涉及5 种不同温度(-20、-10、0、10 与25 ℃)，每一温度下考虑9 种不同汽车行驶工况对锂电池进行测试，具体包括Cycle_1 工况、Cycle_2 工况、Cycle_3 工况、Cycle_4 工况、NN 工况、HWFET 工况、LA92 工况、UDDS 工况以及US06 工况。上述9 种工况中，HWFET、LA92、UDDS与US06工况是电动汽车常用行驶工况，而Cycle_1、Cycle_2、Cycle_3、Cycle_4 与NN 工况则是由HWFET、LA92、UDDS 与US06工况随机组合而成。Panasonic 18650PF锂电池在测试过程中采用0.1 s 间隔记录电池的端电压、电流、功率、放电量、能量、电池温度、温箱温度以及采样时间等8个指标，整个数据集包含约500万组测试数据。

3.2 数据预处理

本文实验选取Panasonic 18650PF 锂电池数据集中的0、10 和25 ℃三种温度条件下对应的九种行驶工况的相关数据。依据1.1 节，实验采用每组数据中的电池端电压、电流、电池温度与放电量等指标数据，其中，端电压、电流、电池温度分别对应网络模型所需电池特性观测数据[Vτ,Iτ,Tτ]，模型输出则为电池SOC 估计值，其观测值依放电量按定义计算得到。

为消除数据所涉计量单位及其量级的影响，本文对实验数据采取归一化处理。具体地，在数据输入Bi-LSTM/Bi-GRU 等网络模型之前，对所涉电压、电流、电池温度与SOC等指标数据采用[-1,1]归一化，具体如式(15)所示。

式中，xnorm表示归一化后的数据；x 表示初始数据；xmax、xmin表示初始数据中的最大值与最小值。

4 实验结果与分析

4.1 实验环境设定

本文实验所用电脑配置为Intel Core i7-9750H 2.6 GHz CPU、 NVIDIA GeForce GTX 1660Ti(6 GB) GPU 以及16 GB RAM，使用Python 语言结合Tensorflow后端在Keras框架中完成。整体上Bi-LSTM/Bi-GRU 网络模型结构简洁、应用友好，具体由一个输入层、一个Bi-LSTM/Bi-GRU层、一个全连接层以及一个输出层构成。输入层以锂电池的电压V、电流I及温度T的序列数据作为输入，隐藏层内采用LSTM 神经元或GRU 神经元，全连接层的作用则是将隐藏层的多个输出值转换成单一时刻的SOC值传给输出层。具体参照文献[24]搭建网络，同时导入该文献所拟GRU-RNN模型的实验结果与本文所拟方法的实验结果进行对比分析。本文实验相关参数的具体设置如表1所示。

为评价Bi-LSTM/Bi-GRU 网络估计锂电子电池SOC的准确性，本文采用平均绝对误差(MAE)以及最大误差(MAX)两指标，其具体计算式如(16)与(17)所示。

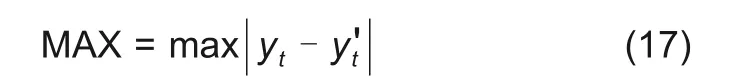
式中，n 为时间序列数据的长度；yt、y't表示在t时刻电池SOC的实际测量值与估计值。

表1 实验所涉网络模型参数设置Table 1 Parameters setting to run the models involved in the experiments

4.2 实验结果分析

如前所述，本文实验基于3 种温度与9 种工况下的相关数据完成，其中，将Cycle_1 工况、Cycle_2 工况、Cycle_3 工况、Cycle_4 工况、NN工况以及UDDS工况的数据作为训练集以训练所涉网络模型，将HWFET工况、LA92工况与US06工况的数据作为验证集以验证网络模型的有效性。具体设置了两个系列的实验，即不同温度条件下所涉网络模型的SOC 估计性能分析以及不同网络参数条件下所拟网络模型的估计性能分析。

4.2.1 不同温度条件下所涉网络的SOC 估计性能分析

实验将Panasonic 18650PF 锂电池数据集中的0、10 及25 ℃三个温度条件下的相关数据整理成三个子集，每个子集分别划分为训练集与验证集以进行训练与验证。进一步，为更深入地比较分析相关模型的估计效果，本文首先将Bi-LSTM/Bi-GRU 网络相关参数设置为与文献[24]中LSTM/GRU 网络相同的参数(如表1 中右边列参数所示)，并采用MAE 指标来对比分析相应估计结果，具体如图7所示。

图7 与文献[24]相同参数设置条件下所涉网络模型的SOC估计结果(MAE)Fig.7 SOC estimation results(MAE)of involved models running with the same parameter settings as presented in reference[24]

由图7不难发现，随温度趋于常温(25 ℃)，各网络模型的估计性能几乎都有所提升。进一步，由图7亦可见，相同网络结构下的双向循环神经网络优于同结构的单向循环神经网络，即Bi-LSTM网络优于LSTM网络，Bi-GRU网络优于GRU网络；但某一网络结构下的单向网络可能会优于另一结构下的双向网络，如图中GRU 网络略优于Bi-LSTM 网络。产生上述情况的主要原因在于，文献[24]中的参数设置是基于GRU-RNN 网络作出的针对性设置，即在该参数设置下的GRU 网络效果达到了最优，但对于Bi-LSTM/Bi-GRU网络而言，同一参数环境未必能够发挥其最优性能。整体而言，在与文献[24]相同的参数环境下，Bi-LSTM/Bi-GRU 网络的估计效果会优于LSTM/GRU 网络，但相对优势并未充分体现，对此，可以通过参数的适当调整以发挥双向循环网络的性能优势。

针对上文所述问题，经一定实验(后文将专门分析网络模型的参数影响)，将Bi-LSTM/Bi-GRU网络参数设置如表1 中间列参数所示。此参数环境下，Bi-LSTM/Bi-GRU网络对锂电池SOC的估计效果较之前述场景得到显著提升。具体所得不同温度条件下的不同网络的SOC 估计曲线如图8 所示。具体地，每个温度条件下的对应子图中，第一行表示SOC 估计曲线，第二行表示估计值与实际测量值的误差曲线。由图8 可见，较之单向网络模型，双向网络模型的SOC估计误差整体上更趋于0值、波幅更小，表明其SOC 估计结果精度更高且更具鲁棒性。与图7 类似，亦可发现随温度趋于常温，各网络模型的SOC估计更趋于SOC真值。为方便细致比较，不同网络模型对应的具体评估结果由表2展示。

图8 不同温度条件下所涉网络模型的SOC估计曲线图Fig.8 SOC estimation curves of involved models under three temperature conditions

表2具体记录了4种网络在0、10及25 ℃三种温度条件下对应验证集上的MAE值与MAX值，并通过简单计算，在Total行中记录了4种网络在三种温度条件下的平均MAE值与最大MAX值。为便于直观上的比较分析，进一步将表2的实验结果转换成如图9 所示的直方图。图9 中，第一行直方图表示MAE 值的变化趋势，第二行直方图则表示MAX值的变化趋势。由图9可见，同一温度条件下，实验所涉MAE 值与MAX 值按LSTM 网络、GRU 网络、Bi-LSTM 网络和Bi-GRU 网络的顺序整体呈下降趋势；随温度趋于常温，各网络模型的SOC 估计性能呈上升趋势。

通过对表2 中相关指标的简单计算，表3 记录下4 种网络在三种温度条件下对应的三个验证集(3×3)上的平均MAE值与最大MAX值，并在Single行中记录当前网络与前一网络性能的提升程度[如(1.083-1.661)/1.611×100%=-34.80%]，在Double行中记录双向网络相较同结构的单向网络的提升程度[如(0.768-1.661)/1.611×100%=-53.76%]。

从整体实验结果来看，4 种网络模型对锂电池SOC 的估计性能按LSTM、GRU、Bi-LSTM 及Bi-GRU网络的顺序依次提高。表3具体反映了上述顺序不同网络模型间的性能提升程度，平均来看MAE 值与MAX 值分别降低了30.06%与21.94%。此外，双向网络性能效果相较同结构的单向网络，MAE 值与MAX 值平均降低了50.75%与35.99%。不同温度条件下各模型可进行类似比较，因本实验的重心在于验证双向学习策略的有效性，故此从略。

表2 不同温度条件下所涉网络模型的SOC估计结果Table 2 SOC estimation results of involved models under three temperature conditions

图9 不同温度条件下所涉网络模型的SOC估计结果直方图Fig.9 Histograms of SOC estimation results of involved models under three temperature conditions

表3 不同网络模型的整体估计性能及相互间的性能提升程度Table 3 A summary of SOC estimation results of involved models improvement

由前述分析可见，本文所构建的Bi-LSTM/Bi-GRU 网络能在不涉及具体电池模型的情况下有效表征锂电池的电压、电流、温度与SOC 之间的非线性关系，所拟模型在三种不同温度条件下的SOC估计中均取得了良好结果。

4.2.2 不同网络参数下的SOC估计性能分析

本节分析不同网络参数条件下Bi-LSTM/Bi-GRU的SOC估计性能。所涉网络参数包括神经元个数、时间步长以及训练迭代次数等。具体地，神经元个数对应Bi-LSTM/Bi-GRU 网络隐藏层中的LSTM/GRU 神经元数量，时间步长表示Bi-LSTM/Bi-GRU 网络输入层的时间深度，训练迭代次数表示Bi-LSTM/Bi-GRU网络的训练周期数。如前，本节实验以MAE 值和MAX 值评价SOC 估计性能，并以相关图表展现。

首先，本节实验考察不同神经元个数对所拟模型SOC 估计结果的影响。具体地，分别取神经元个数为125、250、500 与1000，其余参数设置则与表1中间列参数一致。Bi-LSTM网络模型的相应结果如图10 所示，Bi-GRU 网络模型的结果则由图11 展现。由图10～11 可见，MAE 与MAX 两指标的最优值(以圆圈标记)多集中在神经元个数为250 处，更多的神经元个数并不必然带来SOC 估计性能的提升。与文献[24]的参数设置相比，较低的神经元个数显然能降低网络复杂程度，同时其SOC估计性能却更优良。

图10 不同神经元个数条件下Bi-LSTM网络的SOC估计结果Fig.10 SOC estimation results of Bi-LSTM network with various numbers of neurons

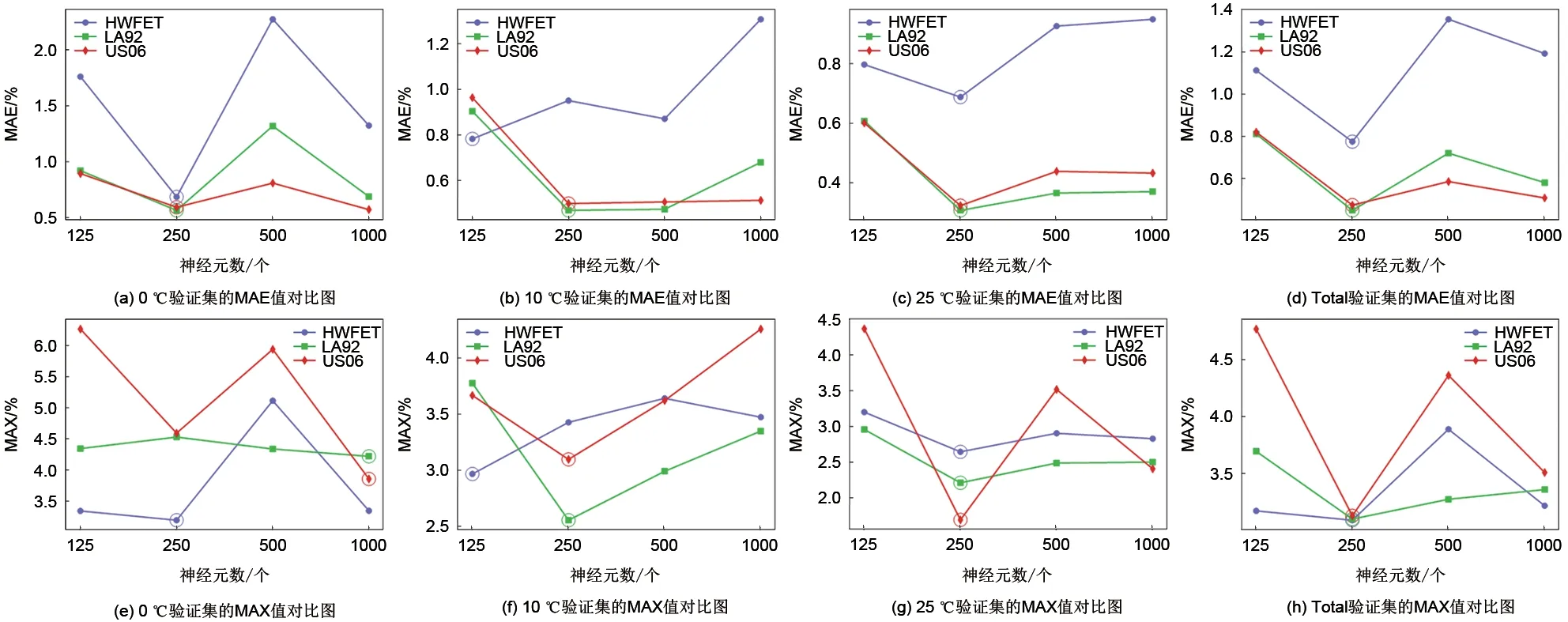
图11 不同神经元个数条件下Bi-GRU网络的SOC估计结果Fig.11 SOC estimation results of Bi-GRU network with various numbers of neurons

接下来考察不同时间步长对所拟模型SOC 估计结果的影响。具体取时间步长分别为500、1000、1500 与2000，其余参数设置则与表1 中间列参数一致。Bi-LSTM 网络模型的相应结果如图12所示，Bi-GRU网络模型的相应结果则由图13展现。由图12～13可见，MAE与MAX两指标的最优值(以圆圈标记)多集中在时间步长为1500处。不难发现，一定范围内较长的时间步长所对应的网络估计性能会有所增加(尤其体现在指标MAE上)，这与锂电池SOC 估计中所蕴含的相关观测量间的长期依赖关系相一致。

图12 不同时间步长条件下Bi-LSTM网络模型的SOC估计结果Fig.12 SOC estimation results of Bi-LSTM network with various time-steps

图13 不同时间步长条件下Bi-GRU网络模型的SOC估计结果Fig.13 SOC estimation results of Bi-GRU network with various time-steps

最后考察不同训练迭代次数对所拟模型SOC估计结果的影响。具体取训练迭代次数分别为40、60、80、100 与120，其余参数设置则与表1 中间列参数一致。Bi-LSTM 网络模型的相应结果如图14 所示，Bi-GRU 网络模型的相应结果如图15 所示。由图14～15可见，MAE与MAX两指标的最优值(以圆圈标记)多集中在训练迭代次数为100 处。一定范围内，随训练迭代次数的增加，网络模型对训练数据有更多次数的利用，模型可以更深层地刻画数据间的非线性关系，但过多次数的复用则亦可带来过学习的风险。

综上，18650PF锂电池数据集上的充分实验表明，本文提出的基于Bi-LSTM/Bi-GRU网络模型的锂电池SOC 估计方法有效可行，较之单向网络模型，能更深入地表征电池内部的非线性特性，具有更高的估计精确与鲁棒性，是具有应用潜力的SOC 估计的有效途径。所拟方法基于数据驱动，对放电平台较长且平的体系，如磷酸铁锂，或有一定局限性，需要结合其他方法探索针对性估计策略。

图14 不同训练迭代次数条件下Bi-LSTM网络的SOC估计结果Fig.14 SOC estimation results of Bi-LSTM network with various training-iterations

图15 不同训练迭代次数条件下Bi-GRU网络的SOC估计结果Fig.15 SOC estimation results of Bi-GRU network with various training-iterations

5 结 论

为提高锂电池SOC 的估计性能，缓解神经网络易发生的梯度消失与梯度爆炸等问题，有效表征电池内部的动态物理与电化学特性，本文引入双向循环神经网络Bi-LSTM/Bi-GRU，以相对容易观测的电池电压、电流与温度等数据作为网络模型输入，降低数据的获取难度，提高实际可操作性。所拟网络模型通过其自身的学习能力将输入观测数据映射为电池的SOC 估计值，实现无直接物理或电化学模型下基于数据驱动的电池内部的非线性特性的有效表征。18650PF锂电池基准数据集上的充分实验表明，双向学习策略能有效提升SOC 估计性能，双向LSTM网络较之LSTM网络，MAE值降低53.76%，MAX 值降低31.28%；Bi-GRU 网络较之GRU 网络，MAE 值降 低47.74%，MAX 值降 低40.70%。本文所拟双向学习策略为纯数据驱动，后期将进一步结合锂电池的相关物理模型或电化学特性，在更契合实际的工作环境中构建SOC 的有效估计模型，提升估计性能的同时增强SOC 估计方法的可解释性。