基于改进随机森林的城市污水处理过程运行数据清洗方法
韩红桂, 赵子凡, 伍小龙, 杨士恒, 何 政, 赵 楠
(1.北京工业大学信息学部, 北京 100124; 2.计算智能与智能系统北京市重点实验室, 北京 100124;3.北京城市排水集团有限责任公司, 北京 100044)
城市污水处理数据是实现污水处理过程运行状态监测、操作优化控制以及故障诊断等环节的重要依据,是提高城市污水处理效率和运营监管水平的信息基础. 由于城市污水处理过程运行环境复杂,多处于泥水混合状态,具有腐蚀性强、干扰多等特点,检测设备获取的数据受污染严重,易出现缺失、离群等异常现象,这为城市污水处理过程数据的分析、处理和运用带来困扰. 如何获取高质量数据、降低异常数据影响已成为污水处理过程数据应用面临的挑战. 为此,城市污水处理厂通常在数据应用过程中采用数据清洗方法,识别异常数据特征,并对异常数据进行剔除和补偿,保证数据的可信度. 然而,城市污水处理过程数据存在异常特征多样,包括离群数据、重复数据和缺失数据等,异常数据难以被识别和重新补偿,导致数据清洗效果不理想.
针对异常数据特征难以识别的问题,基于概率分布的异常数据识别方法被广泛应用. 该方法主要通过分析污水处理过程数据的分布特性,给定正常数据置信区间,当数据超出置信区间时则判定为异常数据[1-2]. 该方法主要适用于变量数据存在可辨识的分布特性,如高斯分布、泊松分布等[3],但污水处理数据采集受进水波动、工况变化影响,往往不完全服从单一的分布特性,导致基于概率分布的分析方法无法准确判别异常数据的存在. 为了提高异常数据识别精度,一类聚类算法通过对比数据或数组之间的相似,分析数据存在的离群特征,能够判别数据异常. 例如,费欢等[4]采用K均值聚类算法计算数据点的聚类中心,并定义异常数据离群距离,判定远离聚类中心的数据为异常数据;黄艳国等[5]设计了改进的模糊C均值聚类异常值识别方法,在模糊C均值聚类算法的基础上加入历史先验数据进行初始聚类中心的优化,用非整数单位化方法对异常值描述;Chen等[6]提出一种改进K均值聚类算法进行异常数据识别,通过最大距离选取初始聚类中心,引入信息熵计算各个属性的权重,计算各样本数据的加权欧氏距离,并依据距离对比判定异常数据. 虽然聚类算法依据样本数据点的距离计算识别异常数据,克服了概率分布方法需要寻找特定概率分布的特性,提高了异常值识别的正确率,但当数据密度大且差异大时,基于聚类算法的异常数据识别方法仅能找出数据的全局离群点,而难以识别局部数据的离群特征. 为此,Breunig等[7]提出了局部离群因子(local outlier factor,LOF)算法,计算邻近数据间距离,根据数据相对于周围邻域的孤立程度,确定异常数据[7]. 该算法虽然解决了基于聚类算法的异常数据识别方法易忽略数据局部异常问题,但通过反复计算邻域距离和密度确定异常数据,计算量大,异常数据剔除效率差.
针对异常数据识别后剔除和补偿,城市污水处理厂通常采用格拉布斯检验方法补偿异常数据. 该方法主要通过依次检验数据中的最值是否属于离群值,并用检验后数据集的中位数、平均数或众数代替[8-9],但该方法用固定数值代替异常数据,与真实数据仍然存在显著差距. 李攀宏等[10]提出了一种双重插值方法,用线性插值方法估计参数,再用拉格朗日线性插值获得待插值数据的校正值,从而获得异常数据补偿值,但污水处理过程变量变化成非线性时变特征,当数据变化剧烈时,线性插值往往不能准确补偿异常值;刘峻清等[11]提出了一种周期时间序列的数据补偿算法,用时间序列分解将污水处理数据划分为趋势项、周期项和残余项,用异常值剔除前的趋势项与周期项之和代替异常值. 该方法能够拟合多种工况下变量数据的变化趋势,并在趋势内插值补偿异常值,但该方法过于依赖异常数据随时间的变化值,对存在复杂变化且连续异常的数据补偿效果较差. 为此,Purwar等[12]在近邻算法研究中给出了处理连续异常数据的补偿方案,该方案在完整数据集中使用样本距离计算数据间的相似度,以若干个最相似完整样本的均值连续补偿异常值;李国和等[13]提出一种基于聚类的递归充填方法,使用同类簇的均值对连续缺失数据进行预填充,并运用同类簇的均值修正异常数据补偿值. 但上述方法过于依赖异常数据近邻域的数据质量,无法针对数据集中任意连续或间断性异常数据进行准确补偿. 为了解决该问题,Zhang等[14]利用T-S模糊神经网络实现数据段任意异常值的补偿,该方法通过真实数据模拟变量数据变化的趋势,并利用在线学习算法和检测数据不断校正网络参数,确保数据集中任意段异常数据补偿的准确性;Peng等[15]提出一种基于反向传播神经网络的数据清洗方法,用遗传算法对神经网络初始权值的阈值进行优化,并借助其他相关变量的有效数据,获得精度较高的异常数据补偿值. 然而,T-S模糊神经网络和反向传播神经网络在进行异常数据补偿前,需要确保训练网络数据的有效,因此还需要其他异常数据识别方法辅助判别数据的有效性. 此外,实际污水处理数据中,异常数据不仅包含单个变量的连续异常或间断异常特征,而且还包含多个变量数据的同步或异步等多种异常特征的混合类型,而现有的异常数据补偿方法还无法针对混合类型的异常数据进行有效补偿.
通过对上述问题的分析,文中提出了一种基于改进随机森林的数据清洗方法,实现对混合类型污水异常数据的清洗. 首先,设计了一个基于孤立森林异常数据识别模型对污水数据的离群点进行识别并剔除;其次,建立了一种改进型随机森林回归模型,实现对数据变化趋势的拟合预测;最后,用改进的随机森林方法对剔除后的数据集进行补偿. 文中提出的随机森林算法不仅实现异常数据的快速识别,同时能够针对混合类型的异常数据进行任意补偿. 综合实验表明,基于改进随机森林的数据清洗方法能够有效清洗混合类型异常数据,提高城市污水处理过程数据的质量.
1 污水异常数据
1.1 污水运行数据特点
城市污水处理过程是一个复杂的工业过程,运行数据是从现场传感器采集到,通过在线监测设备局域网储存到服务器中的数据,为污水处理过程状态估计和性能分析提供依据. 然而,城市污水处理过程数据出现异常现象频率高,易影响数据的处理和使用,常见的异常数据特点如下:
1) 数据缺失严重. 受到检测设备机械或数据传输故障影响,城市污水处理数据易存在丢包现象,导致数据存在连续或间断性缺失;此外,人为的误操作会导致数据的格式化、误分区、误删除等,易引发数据文件丢失.
2) 数据离群度高. 城市污水处理过程具有腐蚀性、时变性等特点,导致设备在线检测的结果易出现较大偏差;同时局限于当前污水处理参数检测技术,当变量波动范围大时,易出现超量程或漂移等现象,导致数据离群度较高.
3) 数据异常随机性大. 根据城市污水处理过程机理分析可知,污水处理过程变量存在相关性,但变量数据发生异常现象相互独立,不同时间随机发生异常,往往在同一检测时段存在单个或几个变量的异常,且异常特征不同(连续或者间断性异常).
1.2 污水异常数据分类
通过对污水原始数据分析可知,污水异常数据主要分为以下3类:离群数据、重复数据和缺失数据. 离群数据是明显偏离其余数值的数据;重复数据为多个时刻出现同一数值的数据,根据污水处理过程动态特性,该类数据被判定为异常数据;缺失数据是某时刻没有采集到的数据或出现数据空缺. 而污水数据变量、参数众多,异常数据不以单一类型出现,往往是以多种异常特征同时出现. 当前对污水数据清洗研究局限于针对单一类型异常数据的清洗方法,尚没有针对不同类型混合的异常数据清洗方法,当沿用传统的概率分布、聚类算法以及智能算法等对不同类型混合的异常数据清洗时,效果仍然难以满足污水处理过程对数据质量的要求. 因此本文提出一种基于改进随机森林的数据清洗方法,以实现对不同类型混合的异常数据进行清洗.
2 异常数据剔除
2.1 孤立森林异常数据识别模型
为了快速准确识别异常数据,文中构建了基于孤立森林(isolation forest,IF)的异常数据识别模型. IF是一种决策树集成学习方法,IF算法首先对已知且连续时间的数据集进行随机划分,然后通过利用异常数据和正常数据的差异性,实现快速准确的识别. 与基于距离的异常识别算法相比,IF算法不需要经过距离或密度计算来识别异常数据,具有较低的计算复杂度[16-17]. IF模型由a棵隔离树组成,如图1所示,算法步骤如下.
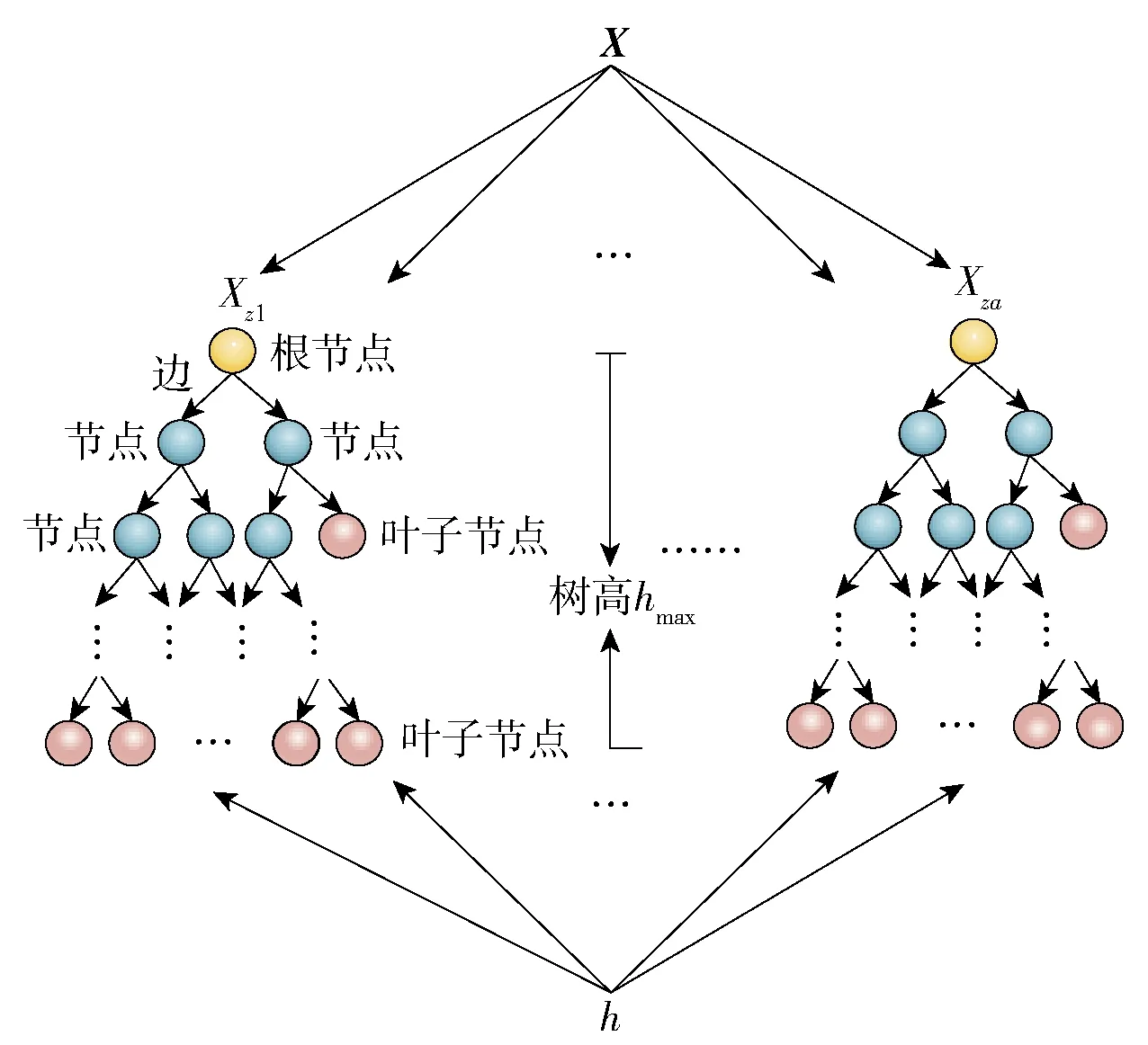
图1 孤立森林模型Fig.1 Isolated forest model
步骤1从训练数据矩阵X中随机抽取一个子样本矩阵Xz,作为第b棵树根节点的集合,其中b=1, 2, 3,…,a,a为根节点的个数,训练数据矩阵X、子样本矩阵Xz用公式表示为
X=[x1,x2,x3,…,xn]
(1)
Xz=[x1,x2,x3,…,xnz]
(2)
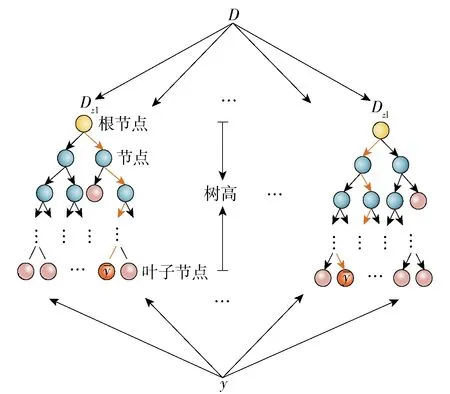
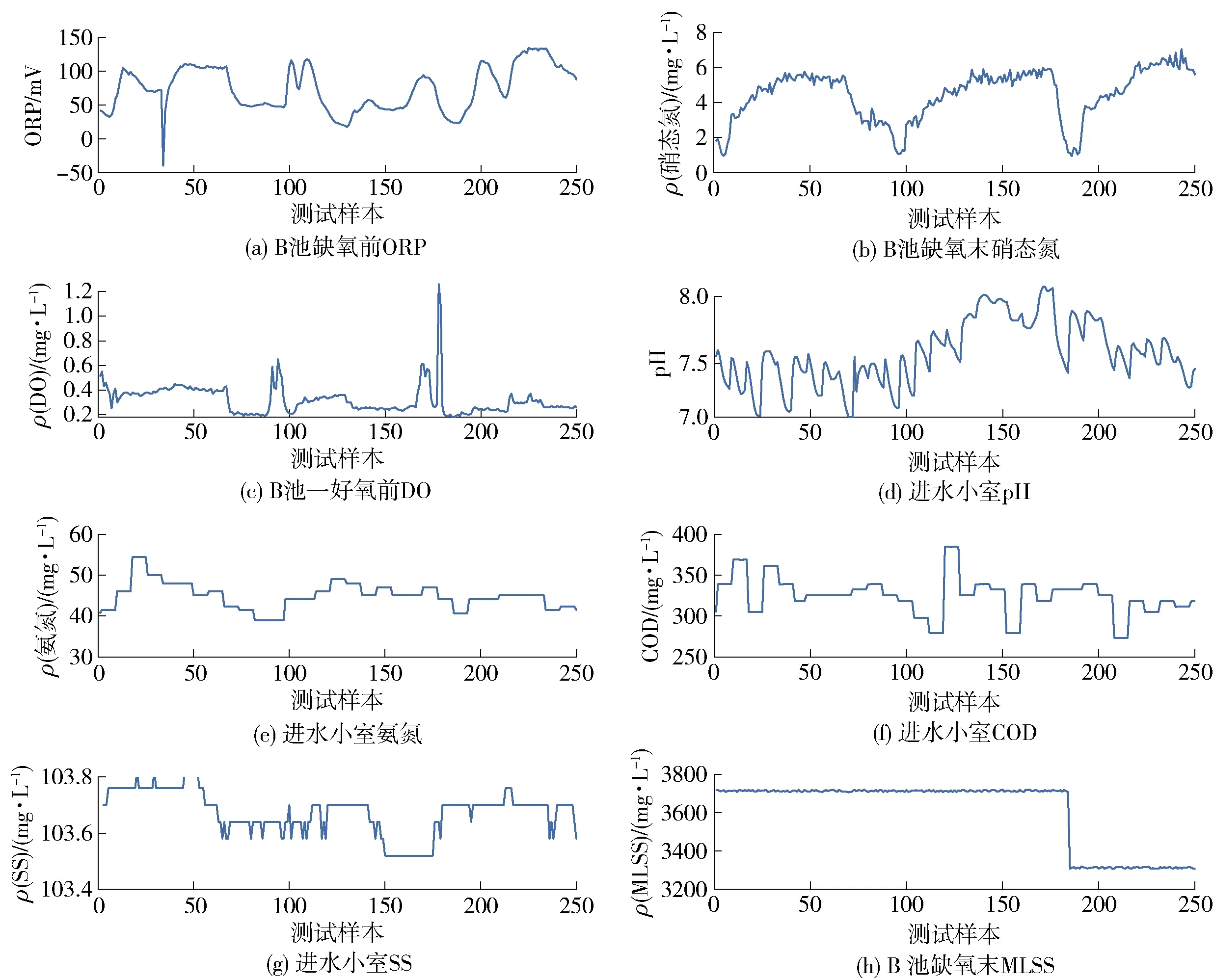
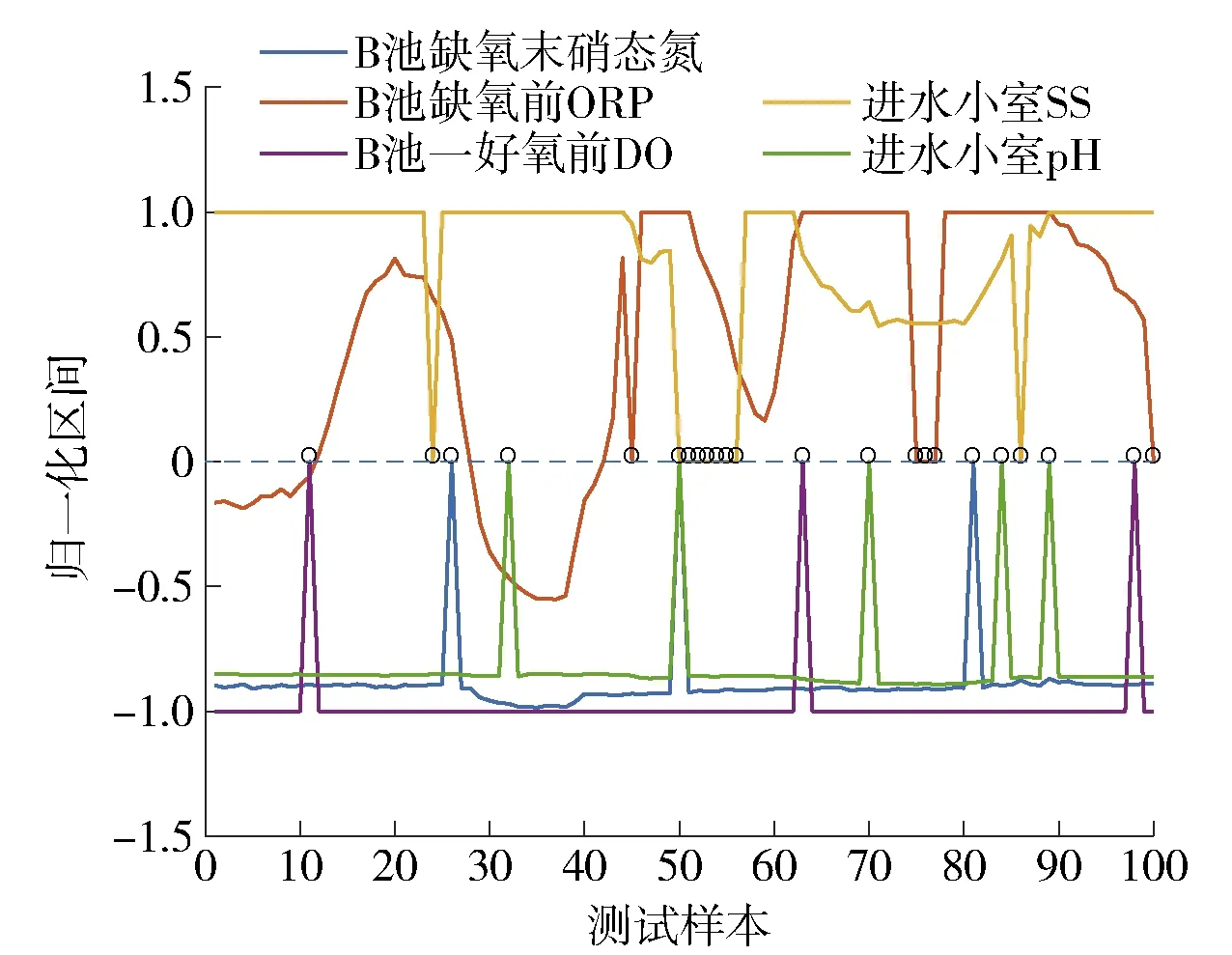
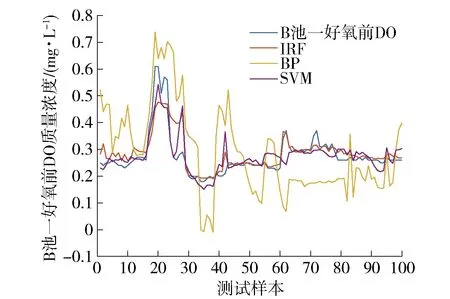
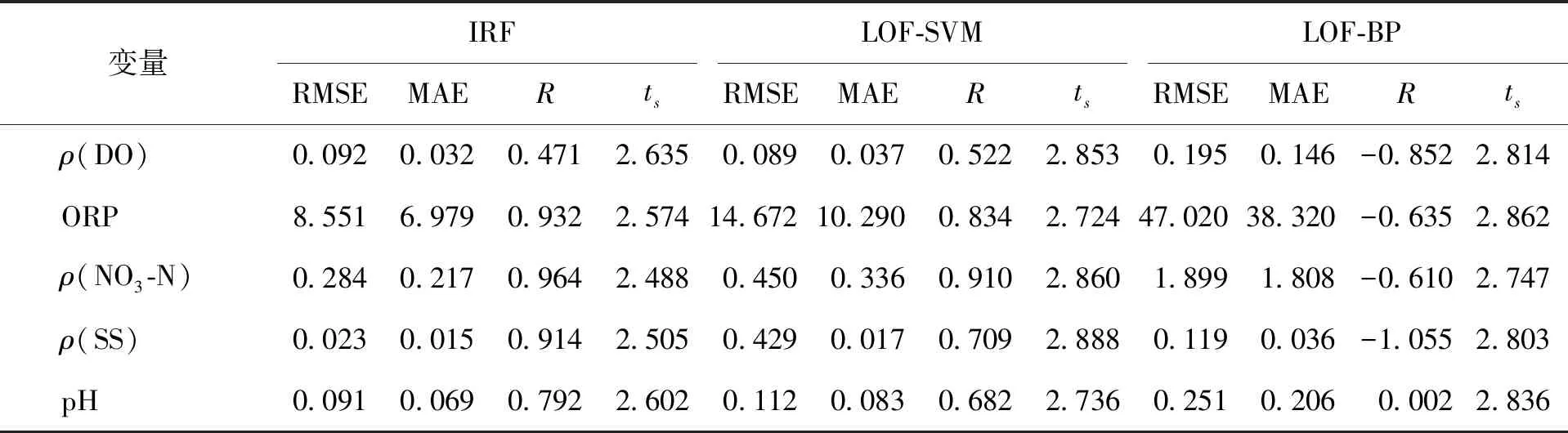
式中:X为m×n维的矩阵,n为变量的个数,m为单一变量包含数据样本的个数;u为样本个数,u=mn;Xz为mz×nz维的矩阵,nz为变量的个数,mz为单一变量包含数据样本的个数,0 步骤2对Xz进行二叉分割:从Xz随机抽取一个列向量xj,j∈{1, 2, 3,…,mz},从列向量xj的集合里随机选择一个切割点T,如式 T=min (xj)+(max (xj)-min (xj))r (3) 所示. 式中r为0到1之间的一个随机数. 若Xz(i,j) 步骤3记录Xleft和Xright所在节点的路径长度hn,hn是从根节点到当前节点经过边的数量. 若hn大于等于树高hmax或节点中的集合个数小于等于mz,则停止训练,完成单棵隔离树的构建;否则对Xleft和Xright再进行二叉划分,重复步骤3. 树高hmax为 hmax=lbu (4) 步骤4如果b IF对X中数据划分隔离,正常数据需要经过多次划分隔离,处在高密度区域;异常数据需要经过少数划分隔离,处于低密度区域. 数据经过IF模型计算后形成不同的高低密度区域,通过计算数据异常值评分反映数据所在密度区域,并对评分高的数据进行剔除. IF模型输出xij的路径长度为hij,xij为矩阵X中的元素,通过hij计算xij的异常值分数,公式为 (5) (6) 式中:C(u)为X中所有数据的平均路径长度;ξ为欧拉常数;E(hij)为数据xij在a棵隔离树中的平均路径长度. 当S(hij,u)的值趋近于0.5时,表明该数据无明显异常状态;当S(hij,u) 的值趋近于1,表明该数据是异常值. 得到每个数据的异常值分数后,结合数据存在等值和缺失特性,将下列3种数据从X中剔除: 1) 将X中异常值分数S(hij,u)大于0.75的xij剔除,用0代替; 2) 将X中缺失的数据用0代替; 3) 将X中连续c1个及以上具有相同数值的xij剔除,用0代替. 异常数据经过剔除后形成不同的数据缺失,根据缺失数据的分布不同将缺失数据划分为不同模式,为选取合适的缺失值处理方法提供参考依据. 将X中3种异常数据剔除后,从中获得3种缺失数据模式:间断数据缺失模式、连续数据缺失模式和水平数据缺失模式. 1) 间断数据缺失模式:缺失值在数据集中随机分布的缺失现象,如公式 xc=[x1,0,x3…,xt,0,xt+2,…,xm]T (7) 所示. 式中:xc为X的列向量,c∈{1, 2, 3,…,n}. 2) 连续数据缺失模式:在某个属性中,出现连续多个值缺失的现象,如公式 (8) 所示. 式中:xp为X的列向量,p∈{1, 2, 3,…,n},lp≪m. 3) 水平数据缺失模式:在某一时刻,多个变量同时出现缺失的现象,如公式 (9) 所示. 式中:Xq为X中q个列向量组成的矩阵,q∈{2, 3, 4,…,n}. 剔除X中的异常数据后,缺失数据将以上述3种缺失模式共同出现,统称为混合类型缺失数据模式,可表示为 (10) 式中:Xh为X中q个列向量组成的矩阵,q∈{2,3,4,…,n},lp≪m. 针对不同缺失数据模式,选择合适方法处理可以提高数据清洗的效率,但目前仍然缺少一种用于混合类型缺失数据模式的数据清洗方法. 为了实现混合类型缺失数据模式的清洗,本文采用改进的随机森林算法进行混合类型缺失数据的补偿. 其中随机森林(random forest,RF)回归是一种回归树集成学习方法,具有避免过拟合、非线性数据拟合能力强等优点,对输入变量个数和数据间耦合性不敏感,且对数据的适应能力强[18-19]. 该算法的RF回归模型是由l棵回归树构成的组合模型,如图2所示. 当输入数据集D经过回归树划分至叶子节点内,取l棵回归树叶子结点的平均结果作为随机森林预测值y. 算法不仅具有多棵回归树建立过程的随机性,同时还保证树与树之间的独立性,增强了模型的泛化能力. 具体算法如下. 图2 随机森林回归模型Fig.2 Model of random forest regression 步骤1从训练矩阵D中有放回随机抽取一个子样本矩阵Dz,作为第v棵回归树根节点的训练样本,v=1, 2, 3,…,l,Dz与D样本大小相同,都是md×nd维的矩阵,nd是变量的个数,md是单一变量包含数据样本的个数,表示为 D=[x1,x2,x3,…,xnd] (11) Dz=[xz1,xz2,xz3,…,xznd] (12) 步骤2对Dz进行分枝生长,从Dz中无放回随机抽取w个(w≪nd)变量,从抽取的每个变量中随机抽取e个值得到切割点矩阵Xcut,表示为 Xcut=[x1,x2,…,xw] (13) 式中Xcut为e×w维的矩阵.xkf是Xcut中的元素,k=1, 2, 3,…,e,f=1, 2, 3,…,w. 计算Xcut集合内的最优切割C(xkf): (14) (15) (16) 式中:Rleft(k,f)为经xkf切分后的左子树集合;Rright(k,f)为经xkf切分后的右子树集合;Q1和Q2分别为Rleft(k,f)和Rright(k,f)中样本数量. 筛选出最小C(xkf)值对应的切割点xkf,若Dz(g,f) 步骤3分别记录Dleft和Dright所在节点路径长度hd和样本大小s,如果Dleft和Dright的hd达到树高或s小于设定阈值,则停止对该节点的分枝生长,否则对子树节点继续分枝生长. 步骤4重复以上步骤,完成l棵回归树的构建,组成随机森林回归模型. (17) 为了适应混合型缺失数据的补偿,对RF算法进行了改进,得到适应能力强的改进型随机森林(improved random forest,IRF)算法. 首先对剔除异常数据的X进行线性插值,再通过矩阵变换得到含有目标补偿变量的填充矩阵;然后用RF回归模型对填充矩阵进行预测,利用集成思想进行tb次输出,取结果均值为补偿值,提高了输出结果的精度,完成混合类型缺失数据的补偿. IRF具体方法如下. 步骤1用线性插值法对X中的缺失值进行插值得到矩阵R,表示为 R=[x′1,x′2,x′3,…,x′n] (18) 式中:R与X样本大小相同,为m×n维的矩阵,n为变量的个数,m是单一变量包含数据样本的个数. 步骤2取X中第i列为目标填充列,R中除第i列外剩余n-1列为相关变量列,形成填充矩阵Rfill,i=1, 2,3,…,n,表示为 Rfill=[x′1,x′2,x′3,…,xi,…x′n] (19) 步骤3从D中有放回随机抽取一个训练矩阵Dzv,完成RF回归模型的建立. 步骤4以Rfill中相关变量列为输入,目标填充列为输出对第i列的缺失值进行预测,得到第t次预测值y(t),t=1, 2, 3,…,tb. 步骤5若t (20) 步骤6若i 实验数据选取2020年6月北京市某污水厂处理过程的真实数据,首先对处理过程的8种关键变量数据变化分析,结果如图3所示. 图3 变量数据曲线Fig.3 Variable data curve 从图3中可以看出B池缺氧末硝态氮、B池一好氧前DO、进水小室pH、进水小室SS、B池缺氧前ORP五个变量趋势变化不稳定,含较大的噪声,数据质量相对较低. 数据清洗实验数据选取该5种变量,每个变量选取500组数据、300组IF训练数据、150组补偿训练数据和100组测试数据. 具体数据清洗实验如下. 为了证明IRF数据清洗方法的效果,实验分别对间断缺失数据、间断缺失混合连续缺失数据、间断缺失混合连续缺失和水平缺失数据3种数据情况做了数据补偿,通过均方根误差RMSE、平均绝对误差MAE、确定系数R[20-21]分析数据清洗结果准确性,R可以表示2个曲线的拟合程度. 计算公式分别为 (21) (22) (23) 式中:N为样本总数;yi为实际值;ypi为预测值;ya为样本平均值. 对500组测试数据集中随机插入15组间断异常数据和10组连续异常数据. 通过IF算法对异常数据识别并剔除,构成含5%缺失值的混合类型缺失数据集,结果如图4所示. 图4 缺失数据分布Fig.4 Missing data distribution map 为便于观察缺失数据的分布,将数据归一化处理后,剔除异常点并用0代替. 图4表示了剔除25组数据后的实验数据分布,并在图中对25组缺失值的位置进行了标记. 其中进水小室SS数据中包含7组连续缺失值和2组间断缺失值;B池缺氧前ORP数据中包含3组连续缺失值和2组间断缺失值;B池缺氧末硝态氮数据、B池一好氧前DO数据、进水小室pH数据分别包含了3组、3组、5组间断缺失值. 其中在第51个样本进水小室SS、进水小室pH、B池缺氧末硝态氮3个变量数据同时缺失. 剔除以上25组数据后构成混合类型缺失数据集,比较IRF、BP、SVM在混合类型缺失数据集下的数据补偿能力. 从图4中可以看出B池一好氧前DO中含有3组间断缺失数据,分别比较IRF、BP、SVM对间断缺失数的补偿能力,结果如图5、6所示. 图5是在B池一好氧前DO实验中IRF、SVM、BP的补偿值预测结果,图6表示IRF、SVM、BP在实验中的误差结果. 从图5中得出IRF、SVM补偿值预测结果与实际数据趋势拟合程度相差无几,并且都优于BP算法的拟合结果;从图6中看出BP算法的结果误差波动幅度较大,IRF和SVM的结果误差波动幅度较小,在小范围内稳定变化,均小于BP的误差变化幅度. 所以IRF和SVM都可以很好地对间断缺失数据进行补偿. 图5 DO预测结果Fig.5 Predicted results of DO 图6 DO测量误差Fig.6 Measurement error of DO 从图4中可以看出B池缺氧前ORP中含有2组间断缺失数据和3组连续缺失数据,形成间断缺失混合连续缺失的数据. 分别比较 IRF、BP、SVM在间断缺失混合连续缺失数据下的补偿能力,结果如图7、8所示. 图7是B池缺氧前ORP中IRF、SVM、BP的数据补偿值预测结果,图8表示 IRF、SVM、BP在实验中的误差. 从图7中观察到BP补偿值波动幅度大,拟合误差也较大,SVM和IRF相对稳定,可以拟合实际数据的趋势. 从图8中可以看出SVM和IRF的误差都在小范围内波动,但IRF的误差波动明显小于 SVM. 所以IRF对于间断缺失混合连续缺失数据的补偿效果更好. 图7 ORP预测结果Fig.7 Predicted results of ORP 图8 ORP测量误差Fig.8 Measurement error of ORP 从图4中可以看出进水小室SS、进水小室pH、B池缺氧末硝态氮含有水平缺失模式数据,进水小室SS数据中含有间断缺失混合连续缺失数据,进水小室pH、B池缺氧末硝态氮中含有间断缺失数据,以上变量形成3种缺失模式混合的缺失数据,分别比较IRF、BP、SVM在间断缺失混合连续缺失和水平缺失数据的补偿能力,结果如图9、10所示. 图9表示IRF、SVM、BP在B池缺氧末硝态氮、进水小室SS、进水小室PH的补偿值预测结果,图10表示IRF、SVM、BP在3组实验中的误差结果. 从图9中可以看出在间断缺失混合连续缺失和水平缺失数据下, IRF、SVM与实际趋势的拟合效果均优于BP;从图10可以看出IRF在进水小室SS和进水小室PH的补偿值预测实验中,误差幅度变化明显小于SVM,在B池缺氧末硝态氮补偿值预测实验中,IRF误差幅度变化与SVM近似,但在第37时刻和第52时刻附近IRF误差明显更小,所以在间断缺失混合连续缺失和水平缺失数据的补偿值预测试中,IRF具有更好的稳定性和准确性,对这种混合缺失数据集补偿效果更好,数据适应能力更强. 图9 预测结果Fig.9 Predicted results 图10 误差结果Fig.10 Error results 从上述3组实验结果可以看出,在混合类型缺失数据集中,IRF相对于SVM、BP具有更小的误差波动和更好的拟合趋势. 分别计算3种数据清洗算法的MAE、RMSE、R和时间ts,如表1所示. 从表1中可以看出在MAE的指标评价中,IRF对B池一好氧前DO、B池缺氧前ORP、B池缺氧末硝态氮、进水小室SS和进水小室PH数据清洗结果的 MAE更小,平均补偿效果更好;在RMSE和R的指标评价中, SVM在B池一好氧前DO实验中的RMSE更小、R更大,对间断缺失数据的补偿精确度更高、趋势拟合性更好,IRF在B池缺氧末硝态氮、B池缺氧前ORP、进水小室SS、进水小室PH实验中具有更小的RMSE和更大的R,所以在不同缺失类型混合的数据集中,IRF的补偿效果优于SVM和BP算法,具有更高的精确度和更好的趋势拟合性. 综上所述,在混合类型缺失数据集中,IRF综合清洗效果比SVM、BP更为精确,数据的清洗效果更好. 更适用于混合类型的缺失数据清洗的问题中. 表1 实验结果对比 针对城市污水处理运行过程中出现混合异常数据的问题,本文提出了一种基于改进型随机森林数据清洗方法. 先用IF算法识别离群数据;再剔除离群数据、重复数据和缺失数据,得到混合类型缺失数据集;最后用IRF算法对混合类型缺失数据集进行补偿. 取实际污水数据验证IRF数据清洗算法的有效性,得到以下结论: 1) IF算实现了对污水数据中离群数据的剔除. 2) 在混合类型缺失数据集中,IRF算法相对于其他算法具有更好的清洗效果,适用于混合类型异常数据的清洗.2.2 异常数据剔除
2.3 混合缺失数据模式
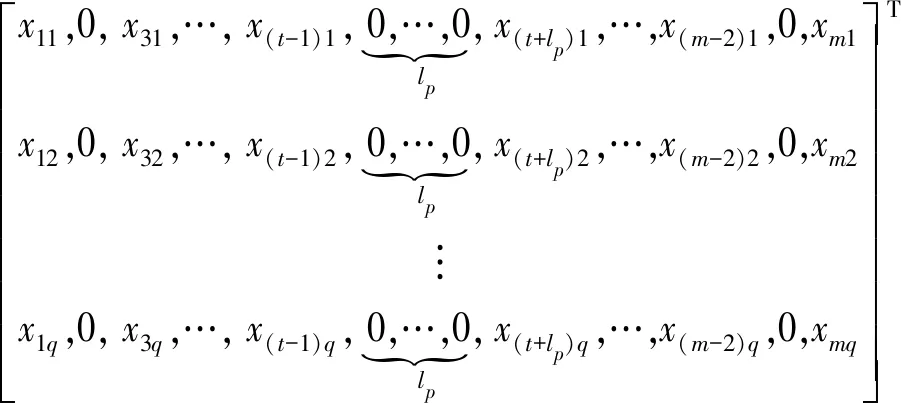
3 改进随机森林数据回归模型
3.1 随机森林回归原理
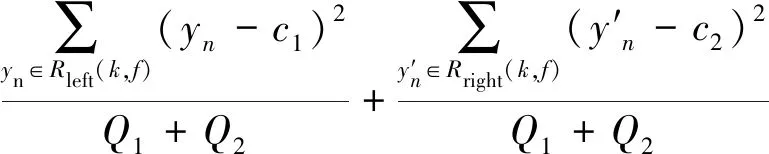
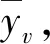
3.2 改进的随机森林回归模型
4 实验与分析
4.1 混合类型异常数据
4.2 间断缺失数据清洗
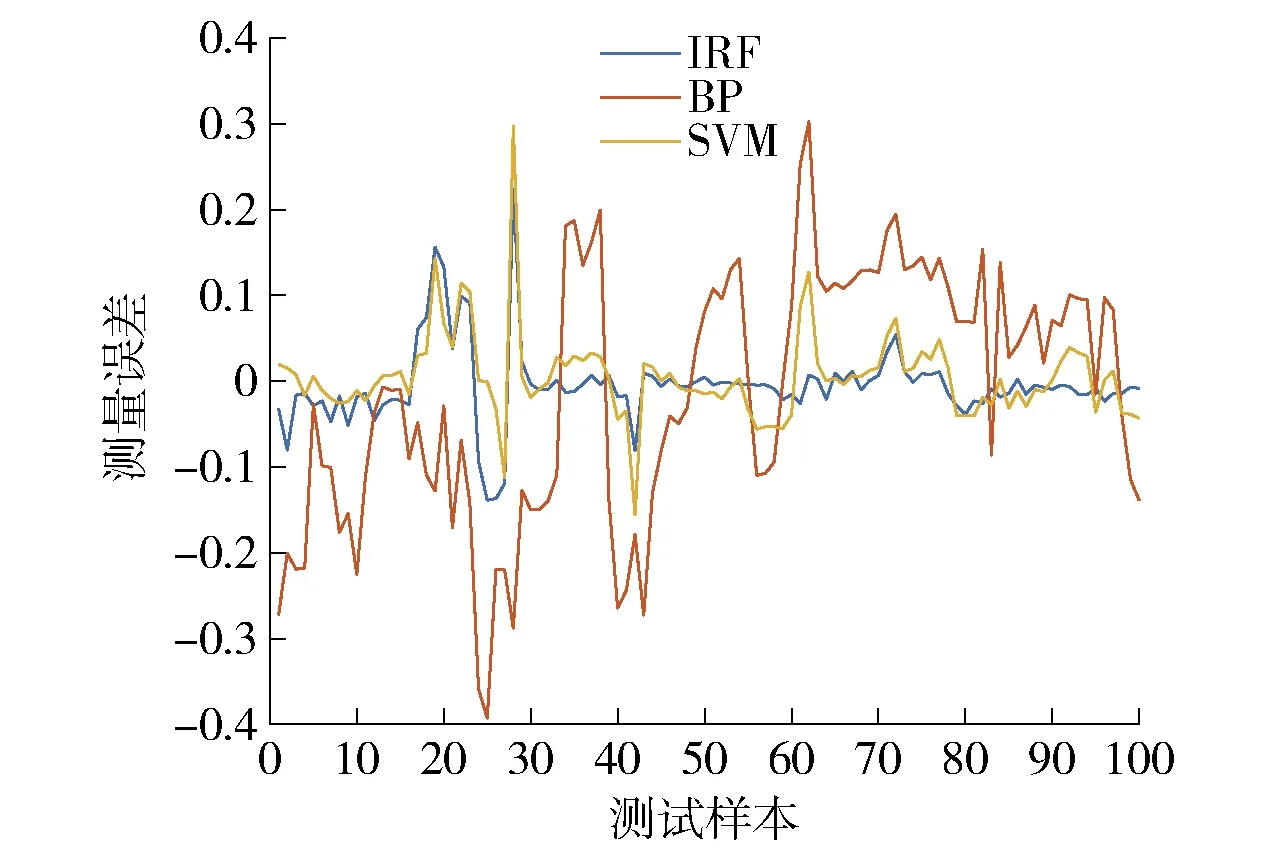
4.3 间断缺失混合连续缺失数据清洗
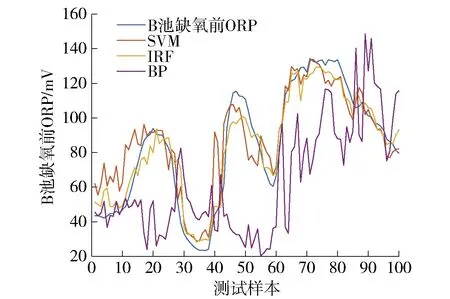
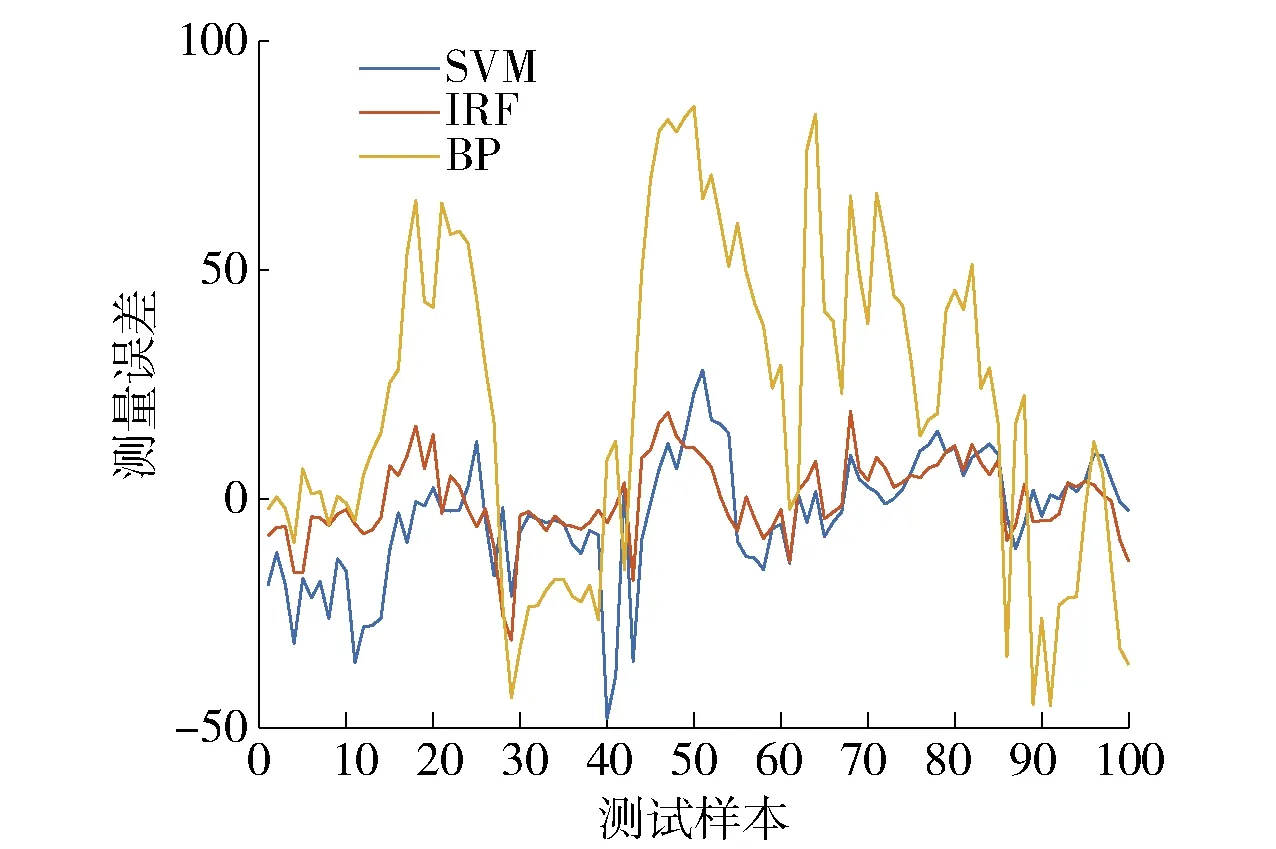
4.4 混合缺失数据补偿
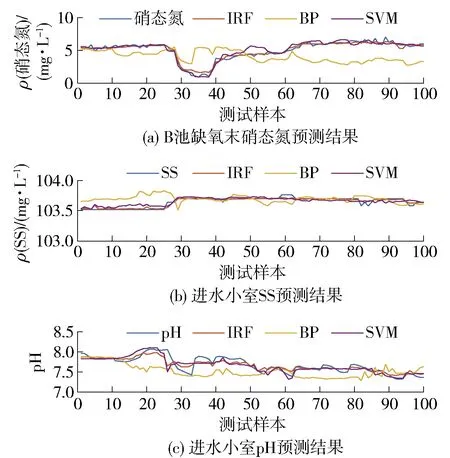
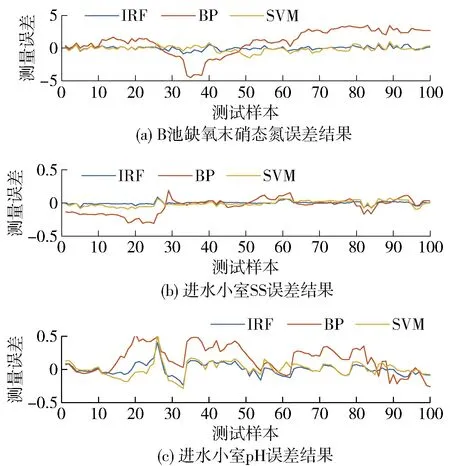
4.5 结果分析
5 结论

