装配式SEMI型浮式筒型基础抗波浪稳定性

王 悦，付茜雅，何文坤，李鹏飞，韩粟宇，王 辉

（1. 北方工业大学 土木工程学院，北京 100144；2. 江苏巨鑫石油钢管有限公司，江苏 扬州 225004；3. 重庆交通大学，重庆 400074）

0 引 言

海上风力发电产生的能源是无污染的可再生能源，目前国际上多采用固定基础结构进行海上风力发电。近些年，随着海上风电的规模不断扩大，为得到良好的收益，通常将风电场建设在深海区。从经济性和技术可行性的角度看，深海风电浮式基础的抗波浪稳定性问题是必须解决的关键问题。

浮式风电基础主要分为张力腿式平台（Tension Leg Platform, TLP）结构基础、单柱式平台（Spar）结构基础和半潜式平台（Semi-Submersible, SEMI）结构基础等3种。近年来，各国学者已针对海上浮式结构物的稳定性开展很多试验研究和数值分析，但仍存在很多问题[1]。

1) 在试验研究方面：Principle Power公司和Hydro Oil & Energy[2]进行了缩尺比例的模型试验研究；Principle Power公司[2]对浮式风电的概念进行了模型试验测试；缅因州大学[3]在荷兰MARIN水池开展了一项名为DeepCwind的模型试验项目，对Spar、TLP和SEMI型平台的水动力性能进行了比较；DUAN等[4]研究了Spar式浮式风机与SEMI型浮式风机的耦合动力性能，结果发现，平台的纵摇运动与纵荡运动的耦合程度较大，塔架顶部的弯矩主要取决于一阶振荡分量；DUAN等[5]对Spar式浮式风机的涡激运动进行了分析，结果发现，风荷载对涡激运动有明显的抑制作用，横荡方向锁定现象的出现时间相对早于纵荡方向；WAYMAN等[6]对TLP与驳船平台进行了对比，结果表明，TLP更适用于深水环境；BACHYNSKIE等[7]对TLP式浮式风机进行了研究，试验结果表明，TLP式浮式风机受固有频率和刚度变化的影响较大，受直径、水深和浮筒半径的影响相对较小。

2) 在数值分析方面：葛沛[8]对TLP进行了静态分析，推导出了平台和张力腿在六自由度方向上的回复刚度；JEON等[9]对Spar式浮式风机在非规则波激励下的动态响应进行了分析；马钰[2]运用频域势流理论对OC3-Hywind Spar浮体进行了频域水动力性能计算，并应用整体时域计算程序对风机进行了整体动力响应计算，分析了风浪载荷对系统动力响应性能的影响。

为探讨装配式SEMI型风机基础的工作特性，在以上研究的基础上，设计适应作业现场的结构形式并开展室内模型试验研究，通过数值模型和室内模型对这类结构进行大量变动参数分析，得到波浪与风机耦合状态下结构的工作机理，获得装配式SEMI型浮式基础的设计和分析理论。

国内外学者对浮式基础的试验研究多集中于Spar式浮式基础和TLP式浮式基础上，对结构形式简单、施工安装易行的SEMI型浮式基础的研究相对较少。已有研究多是针对SEMI型浮式基础进行传统的频域分析和时域分析，对其波浪稳定性的研究较少[10]。因此，本文对SEMI型浮式基础的稳定性进行试验研究和理论分析。

1 装配式SEMI型浮式基础模型抗波浪稳定性试验

1.1 浮式基础模型设计和制作

目前研究的SEMI型浮式基础大都采用浮筒组合的结构形式[11]，该结构形式会影响浮式结构的稳定性，因此本文选择四浮筒三角形式。模型尺寸参考Tri-Floater的参数选取，浮筒等主要结构的尺寸按 20:1的缩尺比确定，对部分与稳定性关系不大的构件进行删减或大比例缩尺。浮式基础原型与试验模型参数对比见表1。

表1 浮式基础原型与试验模型参数对比

筒形基础通过向钢筒内浇筑混凝土制作，混凝土浇筑体积约为钢筒体积的1/3；塔柱采用钢管模拟；桁架采用钢管与扣件拼接成的三角形式浮式平台缩尺模型见图1。

1.2 浮式基础模型抗波浪稳定性试验方法

在重庆交通大学船舶学院水动力实验室进行等效波浪荷载下的稳定性试验。造波池宽19m，长26m，试验时放水深度55cm；采用摇板造波机制造规则波，波高分别为5cm、10cm和15cm，周期为1.5s，每段波持续3min。试验初始阶段，浮筒由静止状态突变为运动状态，此时数值波动规律与稳定之后的波动规律有所不同，相对较大，因此数据采集从第二分钟开始。采用VIC-3D系统对结构上的标识点进行位置跟踪，将标识点运动数据导入主机软件中；以垂直波浪前进方向x、波浪前进方向y和高度方向z为基准建立三维坐标系，根据两标识点的连线在运动前后形成的夹角和标识点的运动范围等参数评估结构在波浪荷载作用下的稳定性。图2为波浪荷载模拟试验示意和试验实景。

图1 四浮筒三角形式浮式平台缩尺模型

图2 波浪荷载模拟试验示意和试验实景

2 抗波浪稳定性试验结果与分析

2.1 塔柱倾角分析

塔柱倾角包含塔柱在波浪前进方向上的投影与z轴的夹角α、塔柱在垂直波浪前进方向上的投影与z轴的夹角β和空间夹角γ。对试验中追踪的各时刻塔柱顶端和底端的标识点位置坐标进行计算，空间夹角计算原理图见图3。塔柱倾角分析结果见图4。空间夹角是指塔柱顶端标识点在各时刻与原始坐标点相比，塔柱前后形成的直线在空间坐标系下的夹角；采集次数是指非接触测量系统对标识点坐标数据进行采集的累计频次；角度差是指相邻的数据采集时刻，标识点塔柱倾角的角度差值，用来衡量塔柱倾角的变化幅度。

浮筒运动期间，上表面边缘在浮筒运动时未淹没至水下即为稳定，经测量可得4个浮筒的入水深度平均值约为30cm，露出水面部分约为40cm，倾覆时角度约为28°。

当波高为10cm时：塔柱沿波浪前进方向的夹角范围为-16°～25°，空间夹角与波浪方向夹角的变化趋势相同，最大角度差为25°；塔柱与垂直波浪前进方向的夹角最大约为3°。当波高为15cm时，塔柱与波浪前进方向的夹角范围为-17°～26°，比10cm波高时略大，但整体结构的运动并没有明显加剧，最大角度差为33°，比10cm波高时增大8°，此时浮筒上表面边缘与水面之间还有一定的安全距离。当波高为20cm时，振动幅度加剧，在数据采集范围内，相邻观测点的最大角度差为35°，比10cm波高时增大2°，且15°的角度差频繁出现，整体表现为塔柱的前进方向与波浪方向的夹角在-23°～26°范围内晃动，范围比15cm波高时大。垂直波浪前进方向最大角度为8°，比10cm波高时增大5°，但整体上看，该结构较为稳定，在3种波浪下的运动并不剧烈。

2.2 塔柱顶点投影区域分析

浮式筒型基础的塔柱在规则波作用下的运动区域可反映浮式基础的运动状态，从而衡量其在波浪荷载作用下的稳定性。利用分析塔柱夹角时建立的三维坐标系，将标识点1的初始坐标转换为坐标原点，并采用相同的方法对相同时刻下的所有标识点进行坐标转换。在试验过程中，塔柱的运动会使坐标原点发生变动，通过消除刚体位移，保证标识点1的坐标始终为坐标原点，对各时刻消除刚体位移之后的标识点0的坐标进行垂直投影处理，在平面内考察其运动区域，塔柱顶点运动区域投影对比见图5。

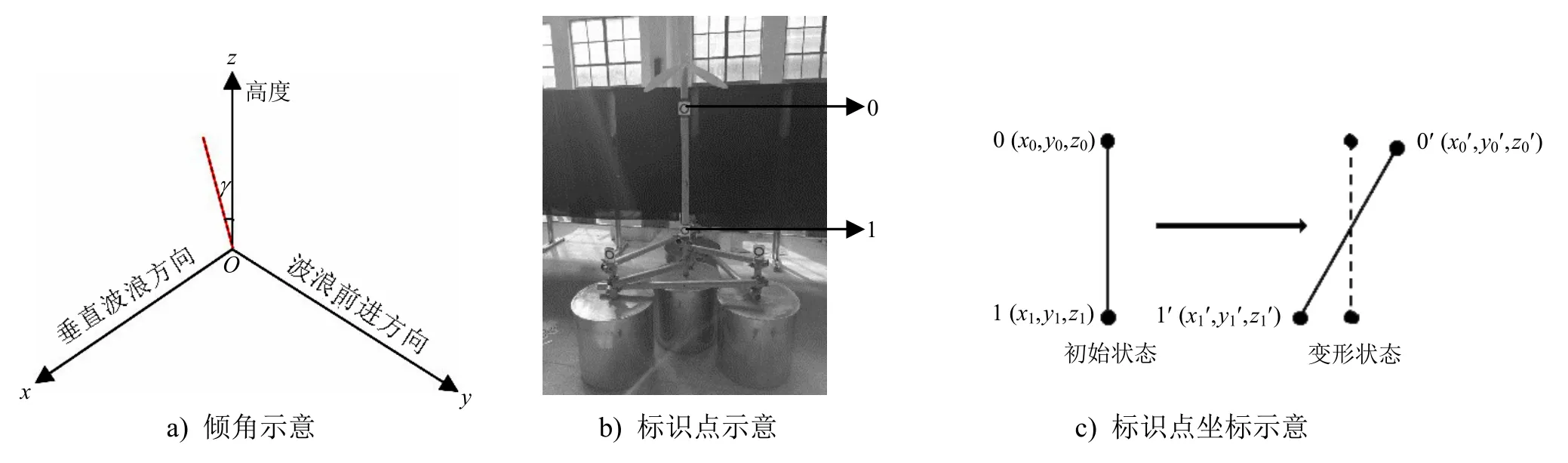
图3 空间夹角计算原理图

图4 塔柱倾角分析结果

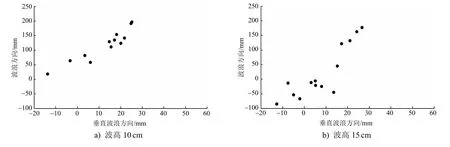
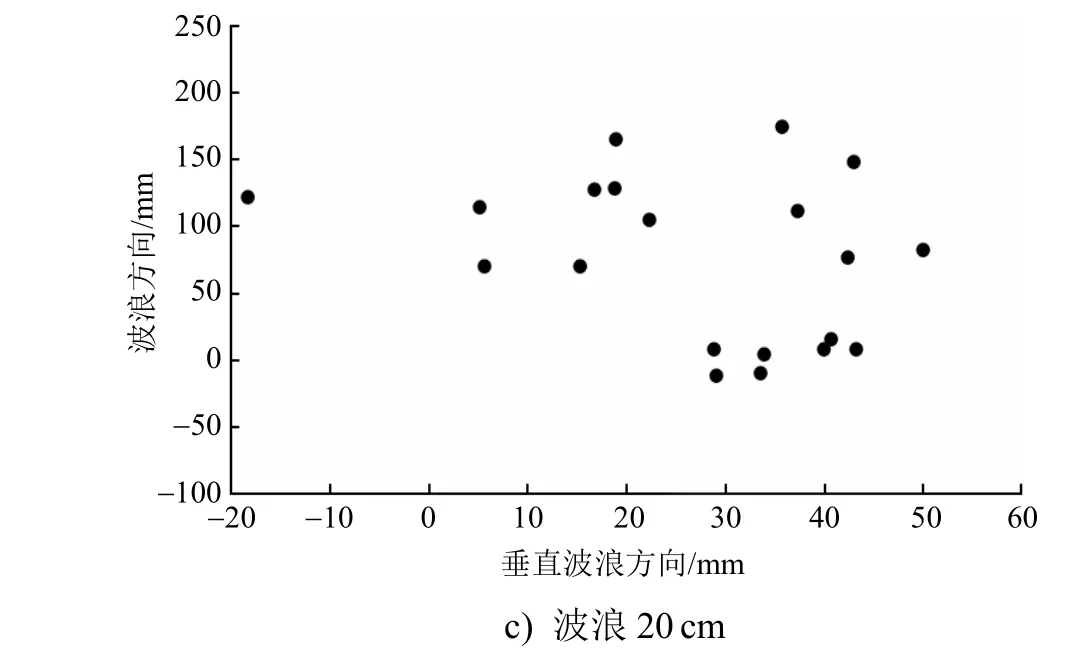
图5 塔柱顶点运动区域投影对比

从图5中可看出，随着波高的增大，塔柱顶点的运动区域增大。当波高为10cm时，浮式筒型基础的塔柱顶点的运动范围为0～200mm，沿垂直波浪前进方向的运动范围为-20～30mm；当波高为15cm时，塔柱顶点的运动范围为-100～200mm，沿垂直波浪前进方向的运动范围为-15～30mm；当波高为20cm时，塔柱顶点沿波浪前进方向的运动范围为-50～200mm，沿垂直波浪前进方向的运动范围为-20～60mm。

2.3 结构运动幅值分析

波高固定为15cm，波浪周期取0.5～3.2s，从0.5s开始，每造波1次，波浪周期增加0.3s，共有10种波频。试验得到各波频下沿波浪前进方向和垂直波浪前进方向的运动范围，对其运动幅度的峰值进行提取，得到结构在各波频下沿波浪前进方向（纵荡）和垂直波浪方向（横荡）的运动幅值（见图6）。

图6 不同波频下结构运动幅值

从图6a中可看出：当波浪周期为0.5s时，结构的运动幅值为260mm；当波浪周期由0.5s变化到1.4s过程中，结构的纵荡运动幅值逐渐增大，到1.4s时达到峰值，最大纵荡运动幅值为350mm，这与塔柱运动区域投影的结果相吻合；在1.4s之后纵荡运动幅值迅速下降，当波浪周期为2.0s时，结构的纵荡运动幅值为280mm，与0.5s时的运动情况大致相似，随后纵荡运动逐渐变缓，到3.2s时纵荡运动幅值为121mm。从图6b中可看出：当波浪周期为0.5s时，结构的横荡运动幅值为43mm，随后逐渐增大，到1.4s时达到峰值73mm；1.4s之后，结构的横荡运动迅速放缓，2.3s时横荡运动幅值为36mm，3.2s时横荡运动幅值为18mm，此时结构的横荡运动已非常缓和。

试验结果表明，模型结构的运动周期在1.4～1.6s，对于波浪周期在该范围内的水域，其各方向的运动将达到峰值，为防止结构在波浪动载荷作用下发生共振，试验时避开了部分频率。在实际工程中，应在结构中设置相关自动设备，改变结构自振周期，避免发生共振。

3 浮式筒型基础结构水动力分析

3.1 频域分析

采用水动力分析软件AQWA进行频域分析，AQWA是一套集成模块，主要用于对各种结构的流体动力学特性进行评估分析[12]。本文采用Graphical Supervisor模块进行频域分析，主要包括浮式基础结构在6个自由度方向上的运动，即横摇roll(x)、纵摇pitch(y)、艏摇yaw(z)、纵荡surge(x)、横荡sway(y)和垂荡heave(z)。以三筒三角形结构形式为例，给出其6个自由度的运动方向示意（见图7），本文所述四筒三角形的6个自由度的运动方向与此一致。

3.2 水动力分析模型建立

采用ANSYS建立四筒三角形结构中4个浮筒的面元模型，试验模型尺寸如表1所示；在AQWA中采用Morison单元建立支撑管架模型，并将其附加在浮筒模型上，结果见图8。

图7 三筒三角形结构6个自由度运动方向示意

图8 浮筒基础AQWA计算模型

3.3 实验室模型频域响应计算结果

基于在实验室对不同波频下结构的运动幅值响应进行试验时的波浪频次，对频次进行补充，取波浪周期为0.5～4.7s，进行波浪扫频，逐级增加0.3s，对四筒三角形形式结构的纵荡和横荡运动情况进行分析，并将所得结果与试验结果相对比，结果见图9和图10。

图9 实验室模型纵荡与频域分析纵荡对比

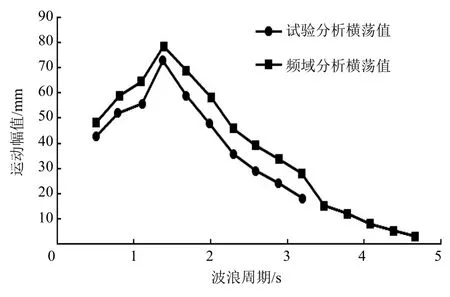
图10 实验室模型横荡与频域分析横荡对比

由图9和图10可知，四筒三角形模型结构在不同波频下的横荡运动幅值和纵荡运动幅值与频域分析结果的变化趋势大致相同。频域分析采用的波浪周期数据比试验时要多，可更好地分析其频域响应规律。总体来看，频域分析结果与试验数据稍有差异，但考虑到试验误差和数据采集偏差，两者结果较为相近，可认为模拟方法正确，验证了构建的模型和选用的模拟方法的可靠性，有助于后续开展浮式基础风电平台水动力响应研究。

4 结 语

本文基于SEMI型浮式基础结构的设计方法设计了一种四筒三角形浮筒组合，并选用该组合形式制作了缩尺比为20:1缩尺的浮式基础风电平台模型。利用VIC-3D系统对结构上的标识点进行了位置跟踪，记录了变动过程，分析了塔柱倾角、塔柱顶点投影区域和结构运动幅值。通过分析，主要得出以下结论：

1) 四筒三角形浮式基础风电平台较为稳定，在3种波浪下的运动并不剧烈。

2) 在实验室模型中，模型的运动周期为1.4～1.6s，对于波浪周期在该范围内的水域，模型各方向的运动将达到峰值，实际工程中，应在结构中设置相关自动设备，改变结构的自振周期，避免发生共振。

3) 采用AQWA软件建立了浮式基础风电平台模型，选用Graphical Supervisor模块对浮式基础风电平台在不同波频下的频域响应进行了数值模拟，模拟结果与试验数据吻合度较高，验证了构建的模型和选用的模拟方法的可靠性。该数值模拟计算结果可供浮式基础风电平台的水动力响应分析参考。