矿物包裹体弹性拉曼频移温压计原理及其地质应用

高晓英 夏梅 周善勇 王思翔

1. 中国科学院壳幔物质与环境重点实验室，中国科学技术大学地球和空间科学学院，合肥 2300262. 中国科学院比较行星学卓越创新中心，合肥 2300261.

通过对变质作用过程中温度/压力等参数的确定，可重建地壳岩石的动态演化过程，示踪长期而复杂的俯冲带构造演化历史。温度和压力是描述地质过程中两个重要的参数，定量地获得岩石所经历的温度和压力条件对于正确认识地质过程、探讨俯冲带过程和构造环境都具有重要意义。目前常用的温压计，包括矿物对温压计(Ferry and Spear, 1978; Koziol and Newton, 1988; Berman, 1991; Holdaway, 2001; 吴春明, 2018)、矿物微量元素温压计(Watsonetal., 2006; Ferry and Watson, 2007; Tomkinsetal., 2007; Haydenetal., 2008)、热力学视剖面模拟(Powelletal., 1998; Holland and Powell, 2011; Whiteetal., 2014; 魏春景等, 2009；魏春景，2016；魏春景和朱文萍, 2016)，这些都是基于元素交换和化学热力学模型为基础发展而成的。然而在俯冲带高压-超高压样品的研究中，常常因后期高温-超高温热事件的叠加，使矿物发生不连续反应或再平衡，导致传统的热力学温压计估算的温压存在较大的不确定性和偏差。而弹性矿物包裹体温压计则是基于力学平衡的，且完全独立于化学平衡之外的，利用激光拉曼频移标定包裹体在常压下储存的残余应力，通过残余应力和矿物物理弹性特性关系，恢复包裹体被捕获时的温度和压力条件。由于该新型弹性矿物包裹体温压计是一种独立于化学平衡之外的力学温压计，因此被广泛应用于示踪俯冲带受后期退变质或后期热事件强烈改造的高压-超高压岩石的变质演化过程(Enamietal., 2007; Korsakovetal., 2009; Ashleyetal., 2014a; Mazzucchellietal., 2018, 2019; Zhongetal., 2018, 2019a; Alvaroetal., 2020; Spear and Wolfe, 2020a, b)，这可以为我们提供来自不同视角的温压信息。

1 弹性矿物包裹体温压计的研究意义与原理

早在150年前熔体包裹体奠基人Sorby (1858)就强调，往往被人们忽略的“小”包裹体却可以揭示“大”的地球科学问题。“There is no necessary connexion between the size of an object and the value of a fact, and …though the object I have described are minute, the conclusions to be derived from the facts are great.” 从被捕获的那一刻开始，包裹体就被圈存在一个与世隔绝的环境中，因此通过对矿物包裹体的详细研究，可以揭示寄主矿物形成时的环境，示踪变质原岩和变质作用的演化轨迹，揭示早期板块构造演化的历史(Audétat and Lowenstern, 2014; Gaoetal., 2017; Ferrero ad Angel, 2018; Alvaroetal., 2020)。

被捕获的矿物包裹体由于受到寄主矿物的圈闭，并不能像自由生长的晶体一样随意延展或伸缩。包裹体被寄主矿物捕获且完全包裹后，由于两种矿物具有不同的弹性特征，随着温压的变化(俯冲折返过程)，两种矿物将产生不同的热膨胀和压缩特性。在俯冲带岩石折返回地表时，包裹体的应力状态不同于施加在寄主矿物上的外部应力或压力，也不同于矿物在地表或在实验室常压条件下测得的岩石压力。此时，矿物包裹体内部存在着残余应力(Rosenfeld and Chase, 1961; Howelletal., 2010)。残余应力(residual stress,Pinc)是指没有外力作用后仍在物体内部存在并自身保持平衡的内应力。而分布在包裹体周围的残余应力除了受控于两相矿物的物理弹性特征外，主要与包裹体被捕获时的P-T条件(Rosenfeld and Chase, 1961; Zhang, 1998; Barronetal., 2008; Howelletal., 2010)及包裹体中的动力学相转变反应(如石英-柯石英转变)有关系。如果了解该动力学过程就可以为我们提供岩石完整的P-T-t演化轨迹(Perrillatetal., 2003)。

矿物包裹体被捕获后由于岩石折返而回到地表，在不考虑岩石发生塑性形变或脆性断裂的情况下，理论上对封存在寄主矿物中包裹体的残余应力通过常规X射线衍射(XRD)(Angeletal., 2014b)或激光拉曼光谱频移方法(Schmidt and Ziemann, 2000; Enamietal., 2007; Ashleyetal., 2014a; Kohn, 2014)定量恢复。但是，由于包裹体被固态寄主矿物介质所包围，寄主矿物的热膨胀或压缩必然导致包裹体应力应变的发生。而且，在多晶面包裹体晶体的棱边或顶点处存在着应力集中的现象，使得晶体内部形成应力分布梯度。这与在静水压力下包裹体的均匀应力应变显著不同。包裹体内部应力应变的非均匀性将导致XRD布拉格衍射峰的展宽(Angeletal., 2007; Zhao and Ross, 2015)。可是，实验室常规的XRD测量的通常是包裹体晶体平均的晶格参数，并不能反映晶体内真实的应力分布(Campomenosietal., 2018; Murrietal., 2018)。而激光拉曼光谱由于具有较高的测量精度和空间分辨率(～1μm小束斑)，可以精确测量封存在寄主矿物中的包裹体局部位置。因此，激光拉曼频移被广泛的应用于限定弹性矿物包裹体残余应力，即包裹体矿物拉曼频移压力计(Raman geobarometry)。此外，将拉曼频移限定的残余应力与矿物弹性特征相结合，可以进一步获得包裹体在捕获时的温压条件(Schmidt and Ziemann, 2000; Enamietal., 2007; Ashleyetal., 2014b, 2015a,b; Kohn, 2014, 2016)，即弹性矿物包裹体温压计(elastic geothermobarometry)。

1.1 矿物包裹体拉曼频移恢复包裹体残余应力

自1928年印度物理学家Raman发现了拉曼散射效应后，拉曼光谱就被广泛应用于物质分子结构的定性或定量研究，近年来也被广泛的应用于地球及行星科学的研究中(Pasteris and Beyssac, 2020)。拉曼光谱谱峰位置通常受控于化学组成、温度和压力。早期大量的研究发现在室温条件下，成分简单的石英拉曼振动模式(Raman active modes)与压力存在着明显的相关性(Asell and Nicol, 1968; Deanetal., 1982; Hemley, 1987; Liu and Mernagh, 1992)。矿物包裹体拉曼频移压力计的理论基础最早来源于Rosenfeld and Chase (1961)的工作，通过分析包裹在石榴石中的具有双折射晕(birefringent halos)的石英晶体包裹体，并基于寄主矿物和包裹体之间存在的弹性效应，根据双折射晕定量估算出石英被捕获时的压力条件(Rosenfeld and Chase, 1961；Rosenfeld, 1969; Adamsetal., 1975)。之后，Hemley (1987)通过系列实验发现，柯石英-石英的拉曼频率与压力有很好的相关性。Izraelietal. (1999)发现，被金刚石包裹的橄榄石中可以保留高达0.13～0.65GPa残余应力，认为Siberian金刚石的源区压力可达4.4～5.2GPa。在包裹体被捕获后，由于石英相对于石榴石具有更高的可压缩性，如果外力发生较大的改变将使两者之间保存较大的应力差，且该应力差能够被拉曼频移所记录(图1)，因此对广泛存在于俯冲带高压-超高压变质岩中刚性石榴石包裹的相对较软的石英来说，是个理想的拉曼频移压力计(Schmidt and Ziemann, 2000; Ashleyetal., 2014a,b; Kohn, 2014; Thomas and Spear, 2018)。为了表述方便，本文中将石榴石中石英包裹体拉曼压力计(quartz-in-garnet elastic geobarometry)简称为QuiG压力计。目前，除了QuiG压力计外，这种弹性矿物包裹体温压计已经被应用于不同的包裹体-寄主矿物对中，包括：石榴石包裹磷灰石(apatite-in-garnet; Ashleyetal., 2017; Barkoffetal., 2017, 2019), 石榴石包裹锆石(zircon-in-garnet; Zhongetal., 2019a)，金刚石包裹石榴石(garnet-in-diamond; Kueteretal., 2016), 绿帘石包裹石英(quartz-in-epidote; Cisnerosetal., 2020)，金刚石包裹蓝晶石(kyanite-in-diamond; Nestolaetal., 2018)，金刚石包裹镁铬铁矿(magnesiochromite-in-diamond; Nestolaetal., 2019)，金刚石包裹橄榄石(olivine-in-diamond; Izraelietal., 1999; Nestolaetal., 2011; Howelletal., 2012)，金刚石包裹方镁石(periclase-in-diamond; Anzolinietal., 2019)，以及在金刚石、石榴石和锆石中柯石英包裹体 (coesite-in-diamond, garnet, and zircon; Parkinson and Katayama, 1999; Sobolevetal., 2000)。由于部分矿物包裹体具有较大成分变化范围，如磷灰石、锆石、蓝晶石等，这些变化的成分会影响拉曼振动峰的频率，而使其应用具有严重的局限性。

图1 石榴石中石英包裹体在室温条件下(红色，基于拉曼频移压力计计算的残余压力7.58kbar)与在1bar压力下(蓝色)拉曼光谱谱图(据Ashley et al. 2014a修改)约15μm石英被石榴石完全包裹且未暴露于表面Fig.1 Raman spectra of quartz at room temperature (red, calculated P=7.58kbar) and 1bar (blue) (modified after Ashley et al. 2014a)An quartz inclusion (～15μm) that is completely encapsulated by garnet

由于矿物包裹体体系与金刚石压腔体系类似，矿物包裹体是自然作用形成的封闭体系，而金刚石压腔是人工形成的封闭体系，故可以在高温高压实验条件下，利用金刚石压腔定量标定矿物包裹体拉曼频移压力计。Schmidt and Ziemann (2000)首次在静水压力场条件下，利用热液金刚石压腔在高温高压条件下(23～800℃，0.1～2.1GPa)对包裹体的拉曼频移进行了温压标定。结果发现，石英拉曼特征谱峰206cm-1频移与温压没有明显的相关性，但是石英464cm-1谱峰频移(ΔVP)沿着-269～600℃等温线与其残余应力(Pinc)具有明显的函数相关性，但是在600℃以内都没有发现等温线的斜率具有温度相关性。对石英464cm-1拉曼谱峰频移与温压进行拟合，得到以下关系方程式：

P(MPa)=0.36079×[(ΔvP)464]2+110.86×(ΔvP)464

其中该式中P为包裹体残余应力，由于该方程式是在23℃的等温线上进行拟合的，进一步根据实验结果对温度进行了内插法校正，将该公式温度适用范围扩大到为-196℃≤T≤560℃,P<20GPa。因为在573℃时，石英发生α相向β相的转变，所以修正后的公式表达为：

(ΔvT)464,P=0.1MPa(cm-1)=2.50136·10-11·T4+1.46454·10-8·T3-1.801·10-5·T2-0.01213·T+0.29

其中该式中P为包裹体残余应力，MPa；T为温度，℃；而α-β石英相转化是可以通过光学显微镜中明显的干涉色变化予以确定。

1.2 矿物包裹体弹性温压计恢复包裹体捕获时的温度条件

矿物包裹体弹性温压计是通过对在俯冲带内矿物包裹体由于温压条件改变而保留的残余应力，限定包裹体捕获时的温度和压力的一种新型方法。通过对寄主矿物中的矿物包裹体进行激光拉曼频移测定，不论在静水压力场还是非静水压力场，计算的也仅仅只是包裹体在室温下对应的残余应力(Pinc) (Ashleyetal., 2014b)。而残余应力和捕获压力并不等同，它们事实上是两个过程中的不同产物(图2)。包裹体的残余应力主要受控于捕获时的温压条件和矿物的弹性性质(Zhang, 1998; Izraelietal., 1999)。

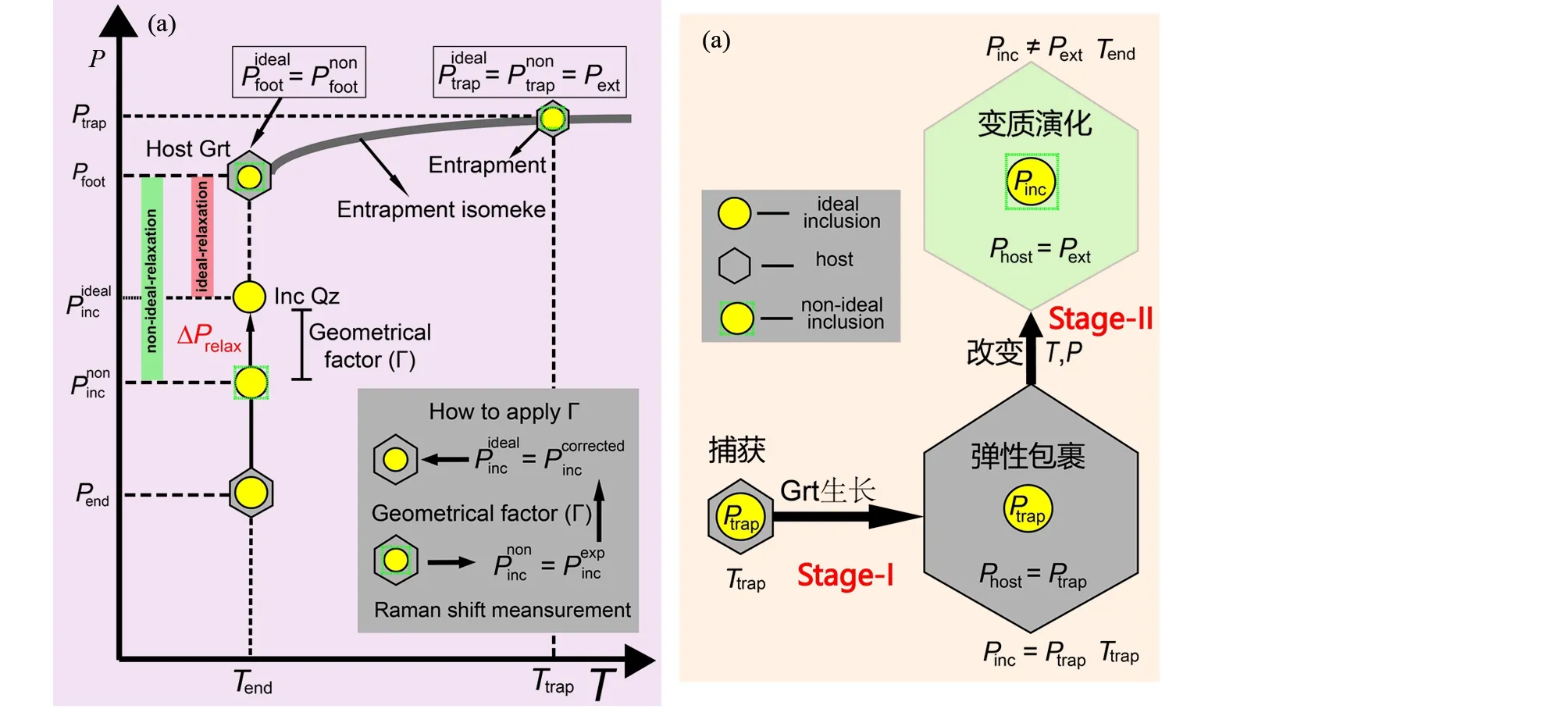
图2 在非静水压力条件下包裹体从被寄主矿物捕获、圈闭和折返过程中变质温压改变导致两相矿物之间的温度和压力变化简图(据Angel et al., 2015; Mazzucchelli et al., 2018修改)Fig.2 Schematic diagram showing calculation procedure for two inclusion-host mineral pairs (modified after Angel et al., 2015; Mazzucchelli et al., 2018)One with ideal geometry (orange dot inclusion). The use of the isomeke concept to calculate residual pressures on an inclusion initially entrapped at Ptrap and Ttrap

在早期第一阶段(图2中Stage I)，包裹体被寄主矿物捕获到包裹体被完全圈闭这一过程中，两者具有相同的温度和压力，且与生长时周围环境条件(Ptrap)相当(图2)，在此过程中两相矿物间的体积分数保持不变，此时没有残余应力，这样的路径被称为“Isomeke”曲线(Adamsetal., 1975)。其瞬时斜率决定于体积热膨胀系数和两相矿物的可压缩性比值，即 (∂P/∂T)isomeke=Δα/Δβ(其中：α为体积热膨胀系数；β为体积压缩系数)(Rosenfeld and Chase, 1961; Zhang, 1998; Howelletal., 2010)，故此时的温压变化值与包裹体和寄主矿物的体积分数比值具有相关性，这是一个纯的热动力学过程。虽然两相矿物的弹性性能并不是一个常数，但是可以通过非线性EoS状态方程表达。Isomeke曲线可根据寄主矿物和包裹体的EoS状态方程，应用EosFit7软件限定(Angeletal., 2014a)。由于硅酸盐矿物之间只有相对较小的Δα/Δβ系数，因此Isomeke曲线一般相对较平坦(Angeletal., 2015)。在晚期第二阶段(图2中Stage II)，包裹体从被完全圈闭到最后被带回到地表，即在岩石俯冲或折返过程中，温压条件发生显著变化，结果使包裹体与寄主矿物发生弹性矿物的膨胀或压缩而产生残余应力，此时的温压变化将偏离Isomeke曲线(Angeletal., 2015)。此时，当包裹体的压力大于外界压力时，包裹体的残余应力为正压(overpressure)，当包裹体的压力小于外界压力时，残余应力为负压(underpressure)。两相矿物的物理性质是定值，故包裹体的残余应力只与外界温压有关。

因此，理论上通过Isomeke曲线结合拉曼频移压力计限定的残余应力，可以准确限定包裹体被捕获时的温压条件，即寄主矿物石榴石生长时的温压条件(图2)(Izraelietal., 1999; Enamietal., 2007; Ashleyetal., 2014a, 2015a, b; Kohn, 2014; Spearetal., 2014; Alvaroetal., 2020; Spear and Wolfe, 2020a, b)。

2 矿物包裹体拉曼弹性温压计影响因素及校正

根据矿物包裹体形成的理论，在拉曼弹性矿物包裹体温压计的应用中，显然最简单的体系是包裹体和寄主矿物都是各向同性矿物，如弹性各向同性的寄主矿物捕获了一个球形或椭圆形的单晶包裹体，当外界发生温度或压力的改变时，寄主矿物会对该包裹体施加一个各向同性的应力，即包裹体处于类似于一个均匀的静水压力(hydrostatic pressure)场。然而，地质样品的应用上存在着多复杂性，如：自然界存在的所有矿物晶体都是弹性各向异性，各向异性的矿物包裹体沿着不同晶轴方向具有不同的应力应变关系，即包裹体受到的是非静水压力场(deviatoric or non-hydrostatic pressure) (Eshelby, 1957)；高压-超高压岩石在折返回地表的过程中，特别是由于在高温超高温条件下会促使超压的包裹体发生弹性驰豫(elastic relaxation)；寄主矿物的固溶体成份以及包裹体几何结构特征都会影响对包裹体捕获温压条件的限定。

2.1 静水vs.非静水压力场

显然这是一种理想的情况：基于假设石英包裹体和寄主石榴石都处于均匀静水压力场条件，然后通过测量石英特征谱峰(464cm-1)的拉曼频移限定包裹体残余应力(Enamietal., 2007; Ashelyetal., 2016; Thomas and Spear, 2018)。而事实上自然界存在的矿物晶体都表现出弹性各向异性，而各向异性的矿物包裹体在受到外界影响，即温压条件发生变化后，沿着不同晶轴方向会具有不同的应力应变，即包裹体所处的是一种非静水压力场环境(Eshelby, 1957)。

为了验证静水压力场下，该温压计的合理性，Ashleyetal. (2014a)曾尝试对研究程度较高的天然样品，来自希腊Sifnos蓝片岩中具有多期生长环带的石榴石进行了研究，结果证实该压力计可以准确应用于天然样品的研究中。同时，研究还发现不同温度下其石英包裹体的残余应力在误差范围内一致，这也与分步加热法实验结果相同，认为温度对石英拉曼频移压力计的影响较小。为了方便进一步使用该温度计，Ashleyetal. (2014b)应用MATLAB数字软件建立了QuiB计算程序用于计算包裹体被捕获时的温压条件。该计算程序界面友好简单，其网址是：http://www. metamorphism.geos.vt.edu/Resources.html。尽管如此，Ashleyetal. (2016)在后续的研究中指出，通过模型得出的残余应力和实际测量值之间存在很大差异，发现石英在α-β相转变附近具有较大的热膨胀系数，基于此重新修正该QuiB计算程序。

Thomas and Spear (2018)利用活塞圆筒压机实验将温度提高到700～800℃，压力在0.5～3.0GPa范围内，发现石英的三个拉曼特征谱峰(128cm-1、206cm-1和464cm-1)的频移相同，因此，他们认为弹性各向异性石英对非静水应力场的影响在误差范围内，可以忽略不计。同时将该压力计的应用拓展到高温领域。虽然原理上石英的三个拉曼特征谱峰(128cm-1、206cm-1和464cm-1)的频移都可以用于计算石英残余应力。但是由于在拉曼谱上，464cm-1峰的强度最大，而且随着压力的升高样品荧光增强，相对弱的信号(128cm-1和206 cm-1)会部分被掩盖，此外石英与石榴石在206cm-1谱峰上有部分叠加，这会对压力计产生额外的不确定性(Enami, 2012；Thomas and Spear, 2018)。认为在大部分情况下应使用464cm-1峰的频移与压力的关系，该结果相对较准确(Enamietal., 2007; Ashleyetal., 2016)。Mazzucchellietal. (2019)通过理论计算模拟结果表明，各向异性矿物，如石英、锆石等包裹在准各向异性矿物石榴石中，对于捕获时温压条件的估算影响较小仅在2%以内，因此认为矿物的各向异性对残余应力的影响不大。

Bonazzietal. (2019)通过高温高压活塞圆筒实验证明，封存在榴辉岩相石榴石中的石英包裹体会遭受各向异性的应变，而使包裹体产生一个偏应力，这个偏应力可使包裹体的键长和键角的力学性质发生改变，而使残余应力偏差高达0.7GPa。Murrietal. (2019)通过理论计算也发现，处于非静水压力场下也存在一个较大的偏应力，利用HF/密度泛函理论(Hartree-Fock/Density Functional Theory)，校正了由于偏应力的存在(石英包裹体晶体结构、晶格参数和声子频率发生的改变)造成拉曼频移偏差。认为基于静水压力场条件下会错误地估算包裹体的残余应力，进一步导致限定包裹体捕获时的压力不准确(Korsakovetal., 2009; Campomenosietal., 2018; Murrietal., 2018, 2019; Angeletal., 2019; Bonazzietal., 2019; Alvaroetal., 2020)。

有研究认为，采用声子模格鲁内森张量(phono-mode Grüneisen tensors)和激光拉曼频移，应用Windows程序软件stRAinMAN(下载网址：http://www.rossangel.net)，对非静水压力场条件导致的残余应力偏差进行校正，可以准确限定各向异性矿物包裹体的捕获时的温压条件(Grüneisen, 1926; Barronetal., 1980; Cantrell, 1980; Murrietal., 2018, 2019; Angeletal., 2019; Bonazzietal., 2019)。

2.2 弹性驰豫

俯冲带的高压-超高压变质岩在折返过程中，特别是在高温-超高温环境下会大大促使具有超压的包裹体发生弹性驰豫(elastic relaxation)，这种现象在多个针对天然样品的研究中被发现(Cayzeretal., 2008; Yamamotoetal., 2008; Korsakovetal., 2010)。Angeletal. (2014b)通过矿物弹性理论计算发现哈萨克斯坦地区的Kokchetav超高压变质地体白片岩中石榴石包裹的石英由于弹性驰豫的发生可以引起高达0.51GPa的应力释放。由于通过拉曼频移限定的残余应力在进行温压估计时需要先进行矿物弹性驰豫的校正(ΔPrelax)，这样才能准确获到包裹体被捕获时的温压条件(图2)(Angeletal., 2014b, 2017)。如果不考虑弹性弛豫，将拉曼频移测得的残余应力与两相矿物的状态方程相结合，可以限定包裹体被捕获时的温度和压力条件(Zhang, 1998; Izraelietal., 1999; Guiraud and Powell, 2006; Howelletal., 2012; Kohn, 2014; Kouketsuetal., 2014)。基于非线性状态方程，Angeletal. (2017)建立了GUI Windows程序软件EosFit-Pinc，对弹性矿物包裹体压力计进行了弹性驰豫校正，软件下载网址如下：http://www.rossangel.net。

2.3 矿物几何结构和分析位置

Sobolevetal. (2000)通过天然样品的研究发现，包裹在金刚石中小颗粒的柯石英包裹体具有较大的拉曼频移，拉曼频移标定的残余应力与包裹体尺寸大小有系统性的变化。后来的研究已证实，这种非球形体的包裹体存在着应力梯度的变化(Zhukov and Korsakov, 2015; Murrietal., 2018)。Campomenosietal. (2018)对包裹在石榴石中的两类(圆形和长柱状)包裹体(石英和锆石)通过分步抛光直至包裹体接近抛光面，定量分析包裹体几何结构以及距离抛光面的位置对残余应力的影响。其结果发现，圆形包裹体的拉曼频移基本不变，而长柱状(或多晶面体)不同位置的拉曼频移不同，在矿物的边部残余应力相对较大，由此认为矿物包裹体应力释放的大小和速率不仅受控于包裹体和寄主矿物的晶体结构、尺寸大小等弹性性质，还受控于相对于抛光表面包裹体的晶格轴向(Eshelby, 1957; Zhukov and Korsakov, 2015; Campomenosietal., 2018; Mazzucchellietal., 2018, 2019)。

Mazzucchellietal. (2018) 通过应用有限元法对矿物包裹体引入有限几何因子(Γ)参数进行残余应力校正模拟，结果显示，对韧性寄主矿物包裹刚性包裹体(如长石中蓝晶石包体、石榴石中金刚石包体)会造成较大的影响。但是，对于刚性的寄主矿物包裹韧性矿物，如石榴石中包裹石英，尽管引入了几何因子的校正，但是该校正对压力估计的影响并不大，在温压计误差范围内，甚至认为在实际应用中可以忽略不计。

分步抛光的实验中发现，随着抛光程度的增加，包裹体向外表面逐渐靠近，其应力逐步释放，相应的拉曼频移逐渐减少。在没抛光前测得的残余应力为0.5GPa, 而当抛光55μm且包裹体并未暴露于表面，此时测算的残余应力骤然降到0.2GPa，当包裹体抛光到一半时其残余应力值为0.06GPa (Campomenosietal., 2018)。即在包裹体中心位置处形变量受到的影响最小(Murri et a., 2018)，这一结论符合前人数值模拟(Mazzucchellietal., 2018)和理论计算的结果(Eshelby, 1957; Rosenfeld ad Chase, 1961; Zhang, 1998; Zhongetal., 2019b)。

因此，为了避免后期样品抛光导致残余应力的释放，对分析的包裹体样品要求：包裹体中心距离薄片表面3倍于包裹体的半径。考虑到一般岩石薄片的厚度为30μm，Zhongetal. (2020)建议选择薄片中包裹体直径<12μm的包裹体分析。如果对于形状特别不规则的矿物，同时需要结合寄主矿物石榴石与包裹体石英实际形状，必要时需采用Mazzucchellietal. (2018, 2019)有限元法进行有限几何因子(Γ)进行校正。

2.4 寄主矿物成份

Enamietal. (2007)通过对日本Sanbagawa不同变质级别变质岩中不同寄主矿物中的石英包裹体进行研究，发现：(1)石榴石中石英包裹体的拉曼频移随着岩石变质峰期压力的增加而增加(石英榴辉岩相>绿帘角闪岩相>角闪岩相)；(2)不同寄主矿物所包裹的石英，其拉曼频移有较大的差别，表现为：石榴石≈蓝晶石>绿辉石≈绿帘石。因此，石英包裹体的残余应力不仅与后期叠加的温压有关，还与寄主矿物的弹性参数(体积弹性模量和剪切弹性模量)有关。不同的矿物以及同一矿物的不同端元组分的弹性模量，如寄主石榴石，都有较大的差别(Bass, 1995; Fei, 1995; Wang and Ji, 2001)。经过理论计算，他们在Schmidt and Ziemann (2000)公式的基础上引入了矿物弹性模量参数校正：

4κGrtμGrtΔTΔA}

式中κ为体积弹性模量，μ为剪切弹性模量，ΔA=AGrt-AQtz为寄主石榴石与石英包裹体热膨胀系数差，PQtz为石英包裹体残余应力，ΔT指遭受到的温度改变，即为施加在石榴石上的外部压力(PGrt=Pext)时的温度。

尽管引入了矿物弹性模量参数对压力进行了校正，但是由于目前已知实验标定的石榴石弹性模量参数是纯端元组分(Bass, 1995; Fei, 1995; Wang and Ji, 2001)，这与天然石榴石通常具有混合的固溶体成份相矛盾。尽管不同端元组分对限定的残余应力差可达0.5GPa，但是认为可以对天然样品按成份比例对弹性模量参数采用机械混合，尽管这种方法并不科学，但是对结果的影响很小，在温度计的误差范围内(Enamietal., 2007; Ashleyetal., 2014b)。

2.5 弹性矿物包裹体温压计校正：Isomeke曲线

所有对弹性矿物包裹体温压计的影响因素和校正方法，都是在矿物降压冷却的过程中发生的，即第二阶段(图2中Stage II)。Alvaroetal. (2020)认为，在第一阶段从包裹体被捕获到完全圈闭的过程中，假设矿物是弹性各向同性的，温压条件的改变沿着Isomeke曲线。但是，由于石英是弹性各向异性矿物，实验发现在这一过程中会产生少量的应力差，使计算得到的捕获温压条件出现些许的偏差。有鉴于此，Alvaroetal. (2020)提出一种新的关于弹性各向异性矿物压力校正方法，在充分考虑到矿物包裹体的弹性各向异性的前提下，结合包裹体和寄主石榴石的晶胞参数变化，通过3D成像，对弹性驰豫校正后采用有限元法计算模拟包裹体在a轴和c轴的捕获压力。通过计算的a轴和c轴Isomeke曲线的交点，即石英包裹体捕获时处于弹性平衡时的温压条件，这就是包裹体被捕获时的准确温压条件。

尽管拉曼弹性包裹体温压计在天然的地质样品研究中有一些局限，但是通过目前已发展的基于矿物物理化学及力学弹性特征的研究，不论是非静水压力场、弹性驰豫、还是包裹体和寄主矿物的几何结构和成份，都有较好的校正方法，因此是一个理想的温压计，可以被广泛的应用于示踪俯冲带高压-超高压岩石的变质过程(Enamietal., 2007; Korsakovetal., 2009, 2020; Ashleyetal., 2014a; Mazzucchellietal., 2018, 2019; Zhongetal., 2018, 2019a; Alvaroetal., 2020；Wolfe and Frank, 2020a, b)。

2.6 拉曼光谱仪自身测试误差

弹性矿物包裹体温压计估计的前提条件是，基于激光拉曼光谱仪测试包裹体的拉曼频移，故拉曼光谱仪自身仪器的调试、校准和数据拟合都会对其温压估算造成误差的传递，因此这部分的误差也需要考虑进去。特别是在日常测试过程中，仪器不仅受实验室内的温度、湿度等因素的影响，同时也受限于仪器本身的状态是否稳定，包括不同光栅的切换、不同波长激光器的使用，这些都有可能导致光谱仪测试参数发生变化，而影响仪器的灵敏度和准确度。因此，我们在日常维护仪器时需要对实验室进行恒温、恒压和恒湿的控制，同时在使用拉曼光谱仪进行测试前，可采用内外穿插法对仪器进行实时校准。当然在对拉曼频移进行定量计算时，也需要慎重考虑基线校正和峰面积函数拟合。

3 弹性矿物包裹体温压计的地质应用及展望

与目前广泛存在的传统热力学温压计相比，这种新型弹性矿物包裹体温压计优势在于：这是一种独立于化学热力学平衡之外的力学温压计，可以应用于示踪俯冲带变质演化历史。作为新发展起来的技术和方法，越来越多地引起地质学家的关注，但是现在大量的研究还集中于温压计本身的拟合和校正，对于天然样品的研究还相对缺乏。虽然存在有限的针对天然样品的研究，但是结果却揭示了该压力计不仅与传统热温压计具有很好的一致性，同时具有优越于热力学温压计的性能，因此在地球科学研究方面具有着广泛的应用前景(Schmidt and Ziemann, 2000; Enamietal., 2007; Mouri and Enami, 2008; Korsakovetal., 2009, 2010; Ashleyetal., 2014a; Ferrero and Angel, 2018; Zhongetal., 2018, 2019a; Alvaroetal., 2020; Wolfe and Spear, 2020a, b)。

近来年，学者们成功地将拉曼弹性矿物温压计应用到各类天然样品的研究中，包括矽卡岩(Ashleyetal., 2017; Barkoffetal., 2017)、蓝片岩(Ashleyetal., 2014a)、高压-超高压榴辉岩相岩石(Yeetal., 2001; Enamietal., 2007; Mouri and Enami, 2008; Korsakovetal., 2009, 2010; Gonzalezetal., 2020)以及金伯利岩中榴辉岩和橄榄岩捕虏体(Ashleyetal., 2014a; Zhongetal., 2019a; Alvaroetal., 2020)。近期，Wolfe and Spear (2020a)以位于美国Acadian造山带中出露的富石榴石变沉积岩为研究对象，将QuiG温压计与其它传统的热温压计包括石榴石等值线相平衡模拟，进行系统对比研究。其结果表明石榴石中包裹的石英其拉曼频移的变化与沿造山带的变质等级变化有很好的相关性，而且QuiG温压计与传统温压计估算的峰期温压相一致。这些结果显示出拉曼弹性矿物温压计具有较大的应用范围，不仅仅是一个潜在的优质温压计，而且可用于广泛示踪俯冲带受后期热事件强烈改造的高压-超高压变质信息，进而示踪地球早期俯冲带演化的动力学过程(Zhongetal., 2018; Alvaroetal., 2020)。

3.1 示踪俯冲带变质岩石的压力条件

对大陆深俯冲和超高压变质作用的认识是大陆动力学的重要进展之一(Chopin, 2003; Ernst and Liou, 2008)。继在变质表壳岩石中发现柯石英(Chopin, 1984; Smith, 1984)和金刚石(Sobolev and Shatsky, 1990; Xuetal., 1992)等压力指示性矿物以来，不断有新的超高压指示性矿物和特殊的出溶结构被发现(van Roermund and Drury, 1998; Yeetal., 2000; Dobrzhinetskayaetal., 2006; Liuetal., 2007)。但是，经历过俯冲的陆壳常常由于缺乏长石，从而使很多传统热平衡压力计失效(如石榴石-斜长石压力计)，缺乏中压和高压指示矿物以及该区间的压力限定方法，结果导致对于俯冲带变质岩的压力限定不够连续。由于石榴石和石英存在于较为广泛的温压区间。近年来，石榴石-石英拉曼弹性温压计应用到不同压力条件的岩石中均给出了理想的结果，如低压变质岩石：超高温麻粒岩(印度Madurai; Satoetal., 2009)、高温变泥质岩(日本Ryoke; Kouketsuetal., 2014)和中温角闪岩(日本Sanbagawa和Higo; Enamietal., 2007; Nishiyama and Aikawa, 2011)；高压变质岩石：蓝片岩(希腊Sifno；Ashleyetal., 2014a)和榴辉岩(日本Sanbagawa和挪威Holsny; Enamietal., 2007; Zhongetal., 2019a)；超高压变质岩石：榴辉岩(Korsakovetal., 2009, 2010; Zhongetal., 2018; Alvaroetal., 2020)。这些都指示石榴石中石英拉曼弹性压力计是一个理想的、能够限定俯冲带不同变质压力条件的指示计 (Enamietal., 2007; Korsakovetal., 2009; Ashleyetal., 2014a; Kouketsuetal., 2014; Zhongetal., 2019a)。

3.2 示踪俯冲带变质过程

经历过大陆深俯冲的超高压变质岩，在经历峰期变质作用后，在后期往往会经历高温变质作用的叠加。这在一定程度上改变其矿物组合以及矿物地球化学性质，一方面可能使得传统的基于热力学平衡的温压计所获得的P-T轨迹有所偏差，另一方面使之前的超高压信息在岩石学和化学热力学上被部分或完全抹掉(Zheng and Chen, 2017)。Alvaroetal. (2020)探究了来自俄罗斯雅库斯克Mir金伯利岩中的榴辉岩捕虏体样品，对寄主石榴石中四个石英包裹体进行拉曼弹性温压限定，结果揭示石榴石在进变质相对低的P-T条件下生长，同时捕获了石英包裹体。然后随石榴石一起继续俯冲到～100km的地幔深度(3.0GPa和850℃)条件下，发生超高压变质作用。在如此高的温度下岩石产生的塑性流，会使石英包裹体和寄主石榴石之间发生弹性驰豫而产生压力差，使获得的石英实际压力比外压小～1.5GPa (Angeletal., 2015)。因此，当岩石压力达到3.5GPa时，石英包裹体获得的压力仅仅为2.0GPa，仍处于石英稳定域。此时，岩石被喷发的金伯利岩浆捕虏，快速的喷发上升足以保留包裹体的压力状态(Zhongetal., 2018)。这项工作的研究意义在于，揭示了俄罗斯雅库斯克Mir金伯利岩中榴辉岩捕虏体是变质成因而非岩浆成因，是地壳物质俯冲到地幔深度时被喷出的金伯利岩浆裹挟带出，进一步阐明了地壳俯冲导致克拉通增生的机制。此项研究表明，拉曼矿物弹性温压计是一个理想的示踪古俯冲带指示计，同时有助于我们认识理解矿物包裹体(Ferrero and Angel, 2018)。

3.3 理想的流变学时钟和速率计

当高压-超高压变质岩中包裹体在进变质和退变质过程中被捕获时，达到峰期温压条件发生折返时，由于高温条件下岩石发生粘性蠕变(viscous creep)或/和塑性形变(plastic yield)，此时会导致寄主石榴石与石英包裹体发生弹性驰豫。Zhongetal. (2018)首次将石榴石中石英拉曼弹性温压计与塑性形变理论相结合，准确限定了金伯利岩岩浆上升时间(<4500小时)和超高压变质岩降压折返时间(>17Myr)。此项研究显示，拉曼矿物弹性温压计是一个理想的天然的“流变学时钟”，不仅可以定量制约折返冷却速率和居留时间，而且可以区分岩石来源于快速的岩浆喷发(以小时为时间尺度)还是慢速的变质折返(以百万年为时间尺度)(Yamamotoetal., 2002; Zhongetal., 2018)。

致谢感谢郑永飞、陈意、张聪等的有益讨论和帮助；感谢两位审稿人对本文提出的富有建议性的意见，使得本文得以更加完善。