Lower Bound Estimate of Blow Up Time for the Porous Medium Equations under Dirichlet and Neumann Boundary Conditions
XUE Yingzhen
School of Business,Xi’an International University,Xi’an 710077,China
Abstract. In this paper, we establish the lower bounds estimate of the blow up time for solutions to the nonlocal cross-coupled porous medium equations with nonlocal source terms under Dirichlet and Neumann boundary conditions. The results are obtained by using some differential inequality technique.
Key Words:Lower bounds;Blow up time;Nonlocal source terms;Dirichlet and Neumann boundary conditions.
1 Introduction
In this article,we consider the lower bound of blow up time for solutions of the nonlocal cross-coupled porous medium equations

and continuous bounded initial values

under Dirichlet boundary condition

or Neumann boundary condition

where Ω ∈R3is a bounded region of∂Ω with a smooth boundary, and satisfies thatp>m>1,q>n>1,υis the unit external normal vector in the external normal direction of∂Ω. There are many research achievements on the lower bound estimation of blow up time for the solution of a single porous media equation,see,e.g.,[1-3]. Liu,et al. [1]studied the following nonlocal porous equation with Dirichlet boundary conditions

They have obtained the lower bound of the blow up time of the solution which

and homogeneous Neumann boundary conditions,the lower bound of the blow up time of the solution which

Liu[2]considered Eq. (1.6)with Robin boundary conditions,they have obtained the lower bound of the blow up time of the solution which

Fang and Chai[3]studied Eq. (1.6)with Neumann boundary conditions

the lower bound of the blow up time of the solution which

whenl>0 of(1.5). The lower bound of the blow up time of the solution which

whenl<0 of Eq.(1.5).
To sum up, most of the existing results focus on a single equation,However,studies on the lower bound of blow up time for the equation set(1.1)-(1.5)have not been found.Blow-up at a finite time and lower bound of blowing up time of solution for the parabolic equations are studied in[4,5]. The lower bound of blowing up time for solutions of other similar equations or equation set is shown in[6-9].
Inspired by[4-5], this paper studies the lower bound estimation of blowing up time for the solutions of the porous media equation set(1.1)-(1.5)with non-local source crosscoupling andm>1,n>1 with relevant formulas and some basic inequalities in[9].
2 The some inequalities
This part introduces some important inequalities used in this paper.
Lemma 2.1.(Membrane inequality)

where λ is the first eigenvalue of∆ω+λω=0,ω>0,x∈Ω,and ω=0,x∈∂Ω.
Lemma 2.2.([9])LetΩbe the bounded star region in RN,and N≥2. Then

Lemma 2.3.(Special Young inequality)Let γ be an arbitrary constant,and0 The lower bound of blow up time for solutions of equations under Dirichlet boundary conditions is discussed below. Theorem 3.1.Defines auxiliary functions for s>max{1,p,q,m−1,n−1,3p−2,3q−2}.If(u,v)is a non-negative classical solution of equation set(1.1)-(1.5)and blow up occurs in the sense of measure J(t)at time t⋆,then the lower bound of t⋆is where,The normal number K1,K2,β1is given in the following proof. Proof.Note that When the equations takeDirichletboundary conditions of Eq.(1.4),Eq.(3.2)becomes where First,Hölder inequality is used to estimate the second term ofin Eq. (3.3),and it is obtained that according to Young inequality and equation above,it is obtained that Second,Hölder inequality is used to estimate the first term on the right side of Eq. (3.4),and it is obtained that from the second term on the right side of inequality sign of(3.5)and Hölder inequality,we can know from the first term on the right side of inequality sign of(3.5)and Hölder inequality,we can know using the following Sobolev inequality([10]): where,the second term of Eq.(3.7)can be simplified to by synthesizing Eqs.(3.7)and(3.8),we have based on Lemma 2.1,Eq.(3.9)becomes Combining Eqs.(3.6)and(3.10),Eq.(3.5)becomes where By synthesizing Eqs.(3.4)-(3.11),of Eq.(3.3)becomes Using the fundamental inequality Eq.(3.12)becomes The same derivation method is used to estimate theJ′ 2(t)term in Eq. (3.3): where In order to deal with the gradient terms in Eqs. (3.13)and(3.14),we setandFinally,by synthesizing Eqs.(3.13)and(3.14),we obtain Integrating(3.16)from 0 tot⋆,we obtain This completes the proof of the theorem. The lower bound of blow up time for solutions of equations under the Neumann boundary conditions is discussed below. Theorem 4.1.Define the same measure as(3.1)and the same condition as s. If(u,v)is a nonnegative classical solution to the equation set(1.1)-(1.2)with(1.3)and(1.5),then the lower bound of t⋆is where,the normal number K1,K2,K3,K4,β1,β2is given in the followingproof. Proof.Lemma 2.2 is used to estimate two boundary terms in Eq. (3.2),then where From the second term on the right hand side of Eq.(4.1)and using Hölder inequality and Lemma 2.3,we can know wherer1is an arbitrary constant. The Hölder inequality is used to estimate the second term on the right hand side of Eq.(4.2). We then have Substituting(4.2)and(4.3)into Eq.(4.1),we get where Similarly,another boundary term in Eq.(3.2)is estimated as follows where,r2is an arbitrary constant. Substituting(3.16),(4.4)and(4.5)into Eq. (3.2),we get where The Eq.(4.6)becomes Integrating(4.7)from 0 tot⋆,we obtain Ifl≤0,then,according to Eq.(3.2),we obtain That is, the same measure relation is obtained with Eq. (3.3). Therefore, whenl≤0,the lower bound of blow up time of the equation set (1.1)-(1.2) with (1.3) and (1.5) is consistent with that of Eq. (3.17). Acknowledgments This work is supported by Natural Science Basic Research Project of Shaanxi Province(2019JM-534);Soft Science Project of Shaanxi Province(2019KRM169);Planned Projects of the 13th Five-year Plan for Education Science of Shaanxi Province(SGH18H544);Project on Higher Education Teaching Reform of Xi’an International University (2019B36), and the Youth Innovation Team of Shaanxi Universities. The author would like to deeply thank all the reviewers for their insightful and constructive comments.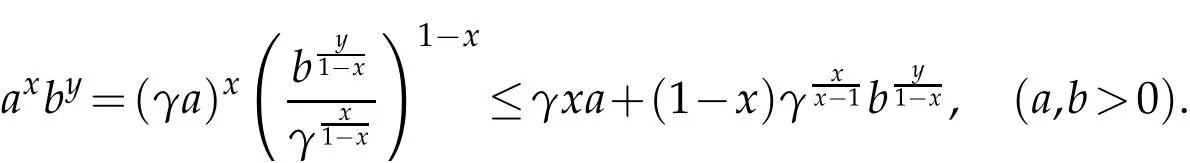
3 Lower bound of blow up time under Dirichlet boundary conditions


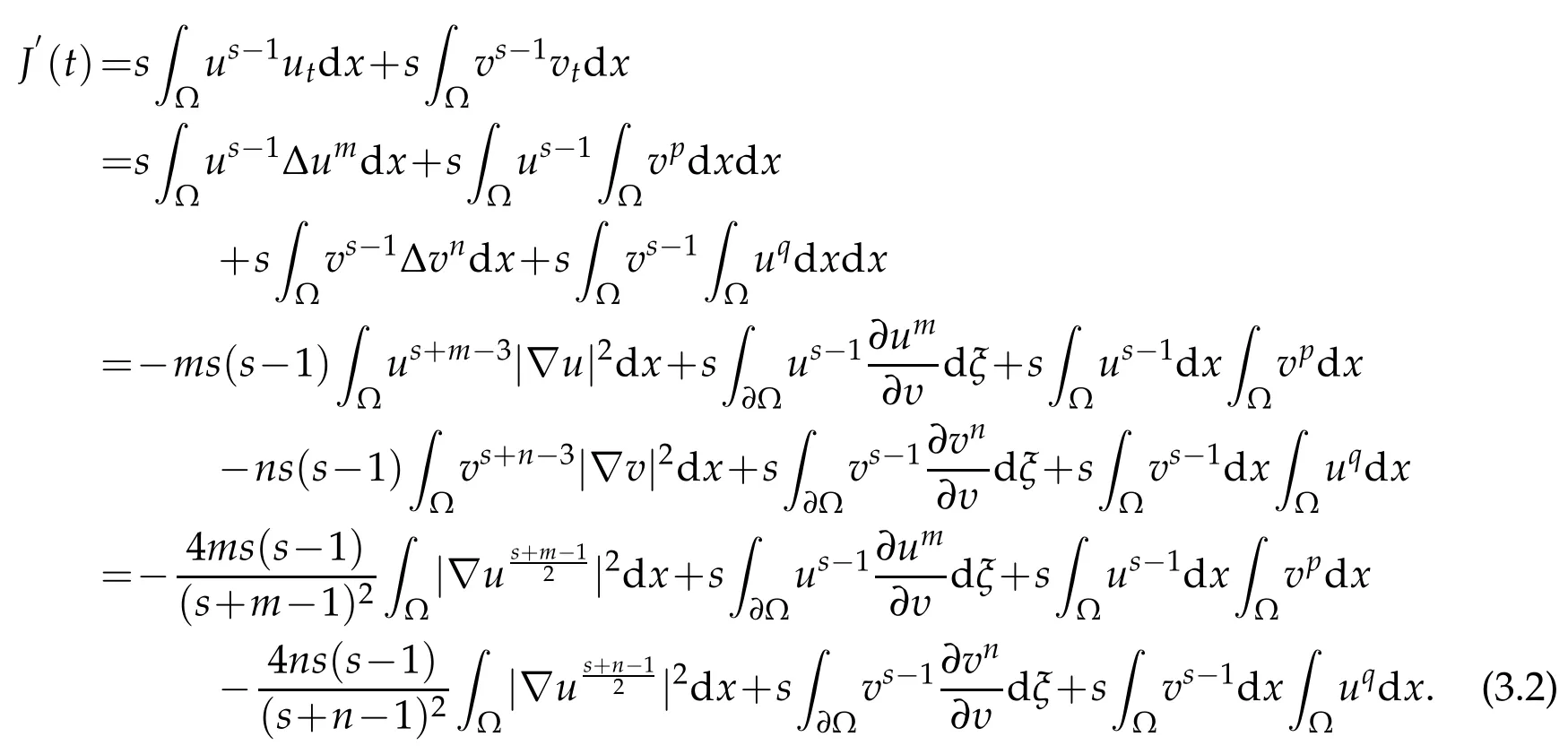

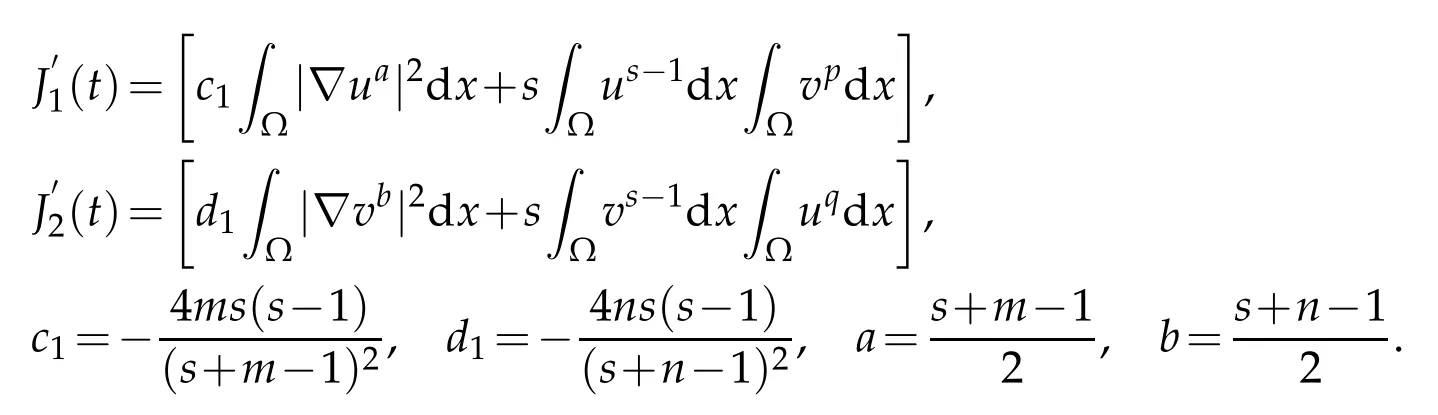
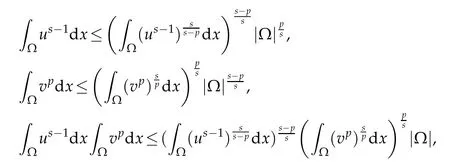




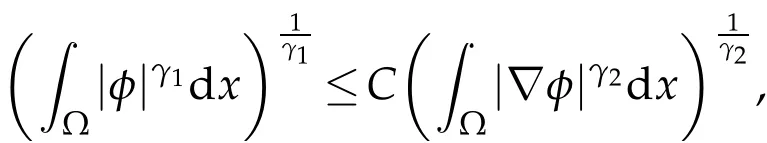

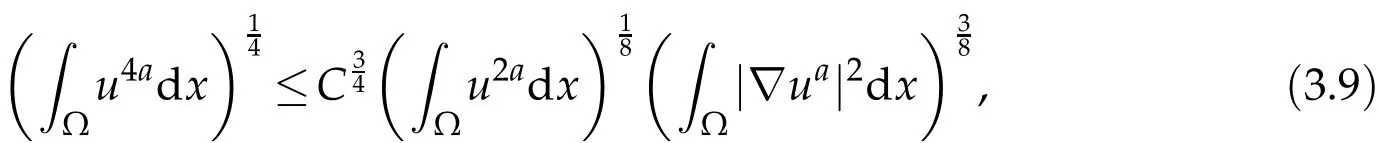



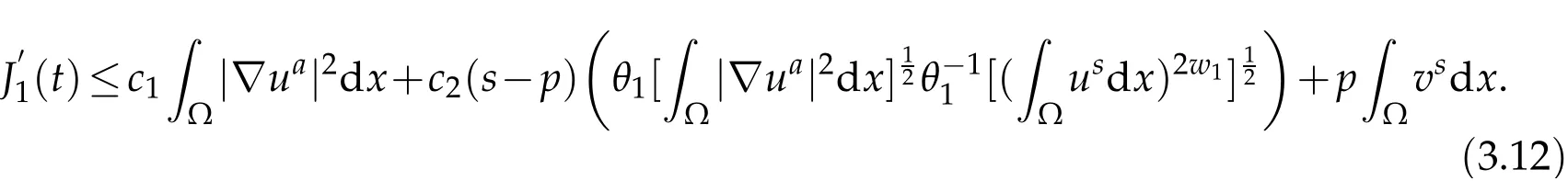



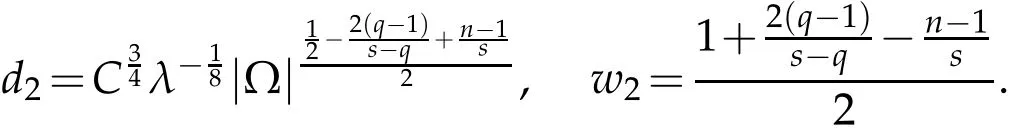



4 Lower bound of blow up time under Neumann boundary conditions
4.1 The case of l>0


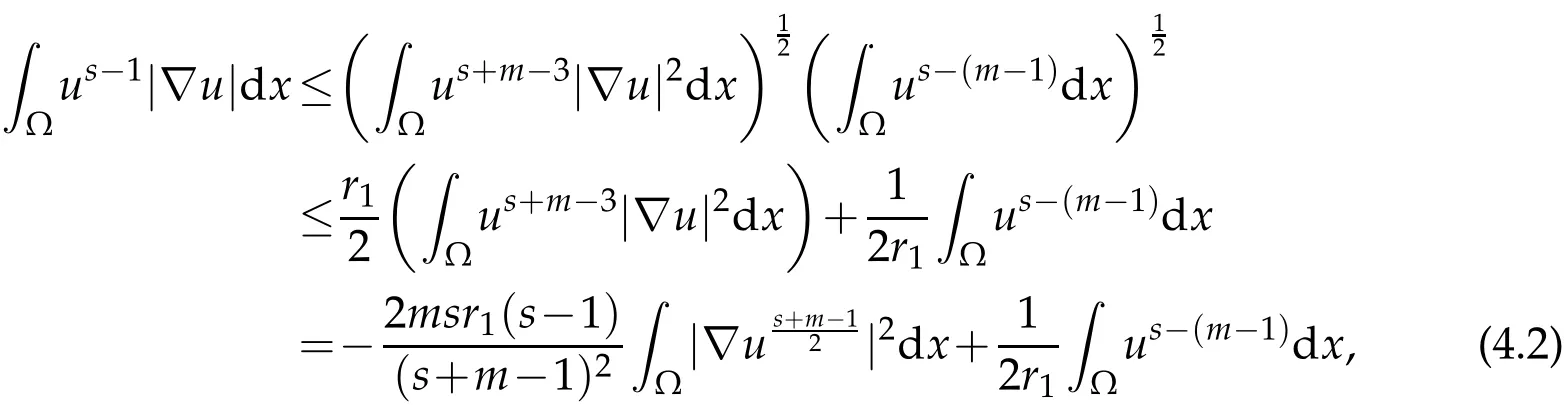


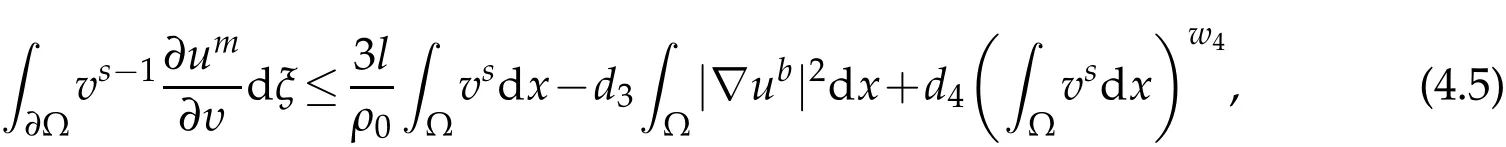




4.2 The case of l ≤0

 Journal of Partial Differential Equations2021年1期
Journal of Partial Differential Equations2021年1期
- Journal of Partial Differential Equations的其它文章
- Fixed Point Theorems in Relational Metric Spaces with an Application to Boundary Value Problems
- Finite-Time Blow-Up and Local Existence for Chemotaxis System with a General Memory Term
- The Averaging Principle for Stochastic Fractional Partial Differential Equations with Fractional Noises
- Remarks on Blow-Up Phenomena in p-Laplacian Heat Equation with Inhomogeneous Nonlinearity
- On Free Boundary Problem for the Non-Newtonian Shear Thickening Fluids
- Global Existence of Smooth Solutions to Three Dimensional Hall-MHD System with Mixed Partial Viscosity
