Fixed Point Theorems in Relational Metric Spaces with an Application to Boundary Value Problems
PRASAD Gopiand KHANTWAL Deepak
1 Department of Mathematics,HNB Garhwal University,Srinagar Garhwal,India.
2 Department of Mathematics,Graphic Era Hill University,Dehradun,India.
Abstract. In this paper, we establish fixed point theorems for generalized nonlinear contractive mappings using the concept of w-distance in relational metric spaces.Thus we generalize the recent results of Senapati and Dey[J.Fixed Point Theory Appl. 19,2945-2961(2017)]and many other important results relevant to this literature.In order to revel the usefulness of such investigations, an application to first order periodic boundary value problem are given. Moreover, we furnish a non-trivial example to demonstrate the validity of our generalization over previous existing results.
Key Words: Binary relation;R-lower semi-continuity;relational metric spaces.
1 Introduction
The classical Banach contraction principle (Bcp)has many inferences and huge applicability in mathematical theory and because of this,Bcp has been improved and generalized in various metric settings.One such interesting and important setting is to establish fixed point results in metric spaces equipped with an arbitrary binary relation. Utilizing the notions of various kind of binary relations such as partial order,strict order,near order,tolerance etc. on metric spaces,many researcher are doing their research during several years(see[1-16])and attempting to obtain new extensions of the celebrated Bcp.Among these extensions,we must quote the one due to Alam and Imdad [8], where some relation theoretic analogues of standard metric notions(such as continuity and completeness)were used.Further,Ahmadullah et al. [14]extended the above setting for nonlinear contractions and obtained an extension of the Boyd-Wong[17] fixed point theorem to such spaces.
On the other hand, recently Senapati and Dey [11] improved and refined the main result of Alam and Imdad [8], Ahmadullah et al. [14] and many others, by utilizing the notion ofw-distance in relational metric spaces,that is,metric spaces endowed with an arbitrary binary relation. Moreover, for further motivation of research in this direction, we refer some important recent generalizations ofw-distance with applications to boundary value problem as well(see,e.g.,[19-21]). It is our aim in this paper to give an extension of these results to nonlinearϕ-contraction and explore the possibility of their application in finding a solution of first order periodic boundary value problem too.
2 Preliminaries
Throughout this chapter,R stands for a non-empty binary relation,N0stands for the the set of whole numbers,i.e.,N0=N∪{0}andRfor the set of all real numbers.
Definition 2.1.([8]).LetRbe a binary relation on a non-empty set X and x,y∈X. We say that x and y areR-comparative if either(x,y)∈Ror(y,x)∈R. We denote it by[x,y]∈R.
Definition 2.2.([8]).Let X be a non-empty set andRa binary relation on X. A sequence{xn}⊂X is called anR-preserving if(xn,xn+1)∈Rfor all n∈N0.
Definition 2.3.([8]).Let X be a non-empty set and T a self-mapping on X. A binary relationRon X is called T-closed if for any x,y∈X,(x,y)∈Rimplies(Tx,Ty)∈R.
Definition 2.4.([14]).Let(X,d)be a metric space andRa binary relation on X. We say that(X,d)isR-complete if everyR-preserving Cauchy sequence in X converges.
The following notion is a generalization ofd-self-closedness of a partial order relation()(defined by Turinici[5-6]).
Definition 2.5.([8]).Let(X,d)be a metric space. A binary relationRon X is called d-self-closed if for anyR-preserving sequence{xn}such that,there exists a subsequence{xnk}of{xn}with[xnk,x]∈Rfor all k∈N0.
Definition 2.6.([14]).Let(X,d)be a metric space,Ra binary relation on X and x∈X. A self-mapping T on X is calledR-continuous at x if for anyR-preserving sequence{xn}suchthat,we have. Moreover,T is calledR-continuous if it isR-continuousat each point of X.
The notion of R-lower semi-continuity (briefly, R-LSC) of a function is defined by Senapati and Dey[11]as follows:
Definition 2.7.Let(X,d)be a metric space and R be a binary relation defined on X. A function f:X→R∪{−∞,+∞}is said to beR-LSC at x if for everyR-preserving sequence xn converging to x,we haveliminfn→+∞f(xn)≥f(x).
By presenting examples the respective authors explained that the R-LSC is weaker than R-continuity as well as lower semi-continuity(see for details[11]) and modify the definition of w-distance ( Definition 2.8) and the corresponding Lemma 1 presented in[18] in the context of metric spaces endowed with an arbitrary binary relation R as follows:
Definition 2.8.Let(X,d)be a metric space andRbe a binary relation on X. A function p:X×X→[0,+∞)is said to be a w-distance on X if
(w1)p(x,z)≤p(x,y)+p(y,z)for any x,y,z∈X;
(w2)for any x∈X,p(x,.):X→[0,∞)isR-lower semi-continuous;
(w3)for any ǫ>0,there exists δ>0,such that p(z,x)≤δ and p(z,y)≤δ imply d(x,y)≤ǫ.
Let Φ be the family of all mappingsϕ: [0,+∞)→[0,+∞) satisfying the following properties
1.ϕis increasing;
Recall that,the necessary condition of any real convergent series ∑nanis that
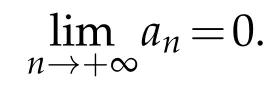
The following two lemmas are required in our subsequent discussion.
Lemma 2.1.([14]). Let ϕ∈Φ.Then for all t>0,we have ϕ(t) Lemma 2.2.([11]). Let(X,d)be a metric space endowed with binary relationRand p:X×X→[0,+∞)be a w-distance. Suppose(xn)and(yn)are twoR-preserving sequences in X and x,y,z∈X. Let(un)and(vn)be sequences of positive real numbers converging to0. Then, we have the followings: (L1)If p(xn,y)≤un and p(xn,z)≤vn for all n∈N, then y=z.Moreover, if p(x,y)=0and p(x,z)=0,then y=z. (L2)If p(xn,yn)≤un and p(xn,z)≤vn for all n≤N,then yn→z. (L3)If p(xn,xm)≤un for all m>n,then(xn)is anR-preserving Cauchy sequence in X. (L4)If p(xn,y)≤un for all n∈N,then(xn)is anR-preserving Cauchy sequence in X. Given a binary relation R and a self-mappingTon a nonempty setX, we use the following notations: (i)F(T):=the set of all fixed points ofT, (ii)X(T,R):={x∈X:(x,Tx)∈R}. In this section,we first consider the existence of fixed points for mappings in relational metric spaces. Theorem 3.1.Let(X,d)be a metric space with a w-distance′p′and a binary relation′R′on X.Let T be a self-mapping on X satisfying the following assumptions: (a) there exists Y⊆X with T(X)⊆Y such that(Y,d)isR-complete, (b)Ris T-closed, (c) either T isR-continuous orR|Y is d-self-closed, (d) X(T,R)is non-empty, for all x,y∈X with(x,y)∈R. Then T has a fixed point. Proof.In the light of assumption(d), letx0be an arbitrary element ofX(T,R).Define a sequence{xn}of Picard iterates with initial pointx0,i.e, Since(x0,Tx0)∈R and R isT-closed,we have so that Thus the sequence{xn}is R-preserving.Applying the contractive condition(e),we have By mathematical induction and the property(Φ1),we obtainp(xn,xn+1)≤ϕn(p(x0,x1)),for alln∈N0.Now,for allm,n∈N0withm≥n,we have Therefore,by(L3),of Lemma 2.2 we have {xn} is an R-preserving Cauchy sequence inY. As(Y,d)is an R-complete,we must havexn→xasn→+∞for somex∈Y. Next we claim thatxis a fixed point ofT. At first,we consider thatTis R-continuous.Since{xn}is an R-preserving sequence with,R-continuity ofTimplies that 会议指出,干部教育培训是干部队伍建设的先导性、基础性、战略性工程,在进行伟大斗争、建设伟大工程、推进伟大事业、实现伟大梦想中具有不可替代的重要地位和作用。制定实施好干部教育培训规划是全党的一件大事,对贯彻落实新时代党的建设总要求和新时代党的组织路线、培养造就忠诚干净担当的高素质专业化干部队伍、确保党的事业后继有人具有重大而深远的意义。 Using the uniqueness of the limit,we obtainTx=x,i.e,xis a fixed point ofT. Alternately, let us assume that R|Yisd-self-closed. So there exists a subsequence{xnk}of{xn}with[xnk,x]∈R for allk∈N0. By using the fact that[xnk,x]∈R,contractive assumption(e)and R-lower-semi-continuity ofp,we have Since R isT-closed and(xnk,x)∈R,so Finally,owing to condition(L1)of Lemma 2.2,we must haveTx=x,i.e.,xis a fixed point ofT. We state the uniqueness related result as follows: Theorem 3.2.In addition to the hypotheses of Theorem 3.1,suppose that any of the assumptions(u1)or(u2)holds: (u1)For every x,y∈T(X)there exists z∈T(X)such that(z,x), (z,y)∈R. (u2)R|T(X)is complete. Then T has a unique fixed point. Proof.In addition to the hypotheses of Theorem 3.1, suppose that condition (u1) hold.Then,for any two fixed pointsx,yofT,there exists an elementz∈T(X),such that Since R isT-closed,we have Applying contractive condition(e),we have Let us considerun=ϕn(p(z,x)) andvn=ϕn(p(z,y)). Clearly, {un} and {vn} are two sequences of real numbers converging to 0.Hence,by(L1)of Lemma 2.2,we havex=y,i.e.,Thas a unique fixed point. Secondly, suppose that in addition to the hypotheses of Theorem 3.1 condition (u2)hold.Supposex,yare any two fixed points ofT. Then we must have(x,y)∈R or(y,x)∈R. For(x,y)∈R,we have which is a contradiction. Hence, we must havex=y. Similarly, if (y,x)∈R, we havex=y. Example 3.1.LetX=[0,+∞) equipped with usual metricd. Then (X,d) is a complete metric space. Define a binary relation (x,y)∈R impliesxyonXand the mappingT:X→Xby Then R isT-closed. Defineϕ:[0,∞)→[0,∞) byfor allt∈[0,∞), and awdistancep:X×X→Xbyp(x,y)=y.Now for allx,y∈Xwith(x,y)∈R,we have so thatTandϕsatisfy assumption (e) of Theorem 3.1. Observe that all the other conditions of Theorem 3.1 are also satisfied. Therefore,Thas a unique fixed point (namelyx=0). Remark 3.1.It is interesting to note that the mappingTin above example does not satisfy the contractive condition of Theorem 2.1 in Senapati and Dey [11]. For example, if we considerx=0 andy=ǫwhereǫis arbitrary small but positive. Clearly,(0,ǫ)∈R and if we take a constantλsuch thatp(T(x),T(y))≤λp(x,y), i.e.thenwhich amounts to say thatλ≥1 so thatλ[0,1). Thus Example 3.1 vindicate the utility of Theorem 3.1 over the results of Sanapati and Dey[11]and many others. Remark 3.2.If we takeϕ(t)=λt, in our main result Theorem 3.1, then we obtain the Theorem 2.1 of Senapati and Dey[11]and if we setp(x,y)=d(x,y),andϕ(t)=λt,in our main result,we obtain the Theorem 3.1 of Alam and Imdad[8]. Hence our main result is an improved and generalized version of relation-theoretic metrical fixed-point theorems of Alam and Imdad[8],Senapati and Dey[11]and many others. As an application, we present a unique solution for the first order periodic boundary value problem equipped with an arbitrary binary relation,wherein our main results are applicable. We consider the following first order periodic boundary value problem: whereT>0 andf:I×R→Ris a continuous function. LetC(I) denote the space of all continuous functions defined onI. We recall the following definitions. Definition 4.1.([9]).A function α∈C1(I)is called a lower solution of(4.1),if Definition 4.2.([9]).A function α∈C1(I)is called a upper solution of(4.1),if Theorem 4.1.In addition to the problem(4.1), suppose that there exist λ>0such that for all x,y∈R with x≤y. Then the existence of a lower solution or an upper solution of problem(4.1)ensures the existence and uniqueness of a solution of problem(4.1). Proof.Problem(4.1)can be rewritten as This problem is equivalent to the integral equation where Define a mappingT:C(I)→C(I)by and a binary relation (i)Note thatC(I)equipped with the sup-metric,i.e.,d(x,y)=sup|x(t)−y(t)|fort∈Iandx,y∈C(I) is complete metric space and hence(C(I),d)is R-complete. (ii)Choose an R-preserving sequence{xn}such that.Then for allt∈I,we get and convergence tox(t) implies thatxn(t)≤z(t) for allt∈I,n∈N0, which amounts to saying that[xn,z]∈R for alln∈N0. Hence,R isd-self-closed.(iii)For any(x,y)∈R,i.e.x(t)≤y(t)then by(4.2),we have andG(t,s)>0 for(t,s)∈I×I,we have which implies that(Tx,Ty)∈R,i.e.,R isT-closed. (iv)Letα∈C1(I)be a lower solution of(4.1),then we must have Multiplying both sides byeλt,we have which implies that Asα(0)≤α(T),we have therefore By using(4.3)and(4.4),we have so that for allt∈I,i.e.,(α(t),Tα(t))∈R for allt∈Iwhich implies thatX(T,R)≠φ. (v)For all(x,y)∈R, so that Now,if we setp(x,y)=d(x,y),then we have whereϕ∈Φ.Hence all the conditions of Theorem 3.1 are satisfied,consequentlyThas a fixed point. Finally following the proof of our earlier Theorem 3.2,Thas a unique fixed point,which is in fact a unique solution of the problem(4.1). Acknowledgement The authors thank the referees for their careful reading of the manuscript and useful comments.3 Main Results

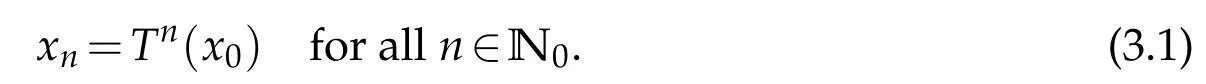




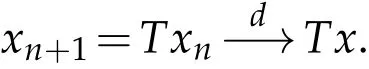
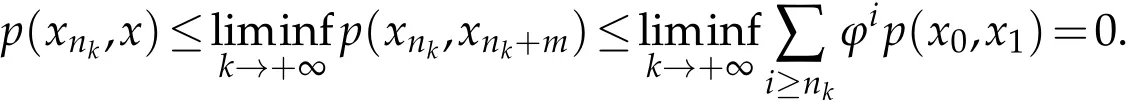

3.1 Uniqueness result


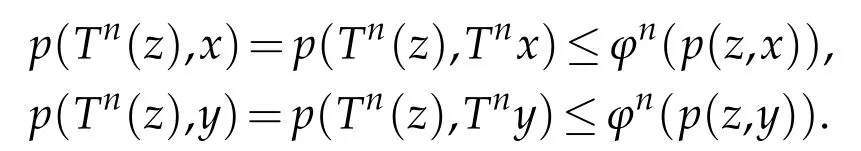
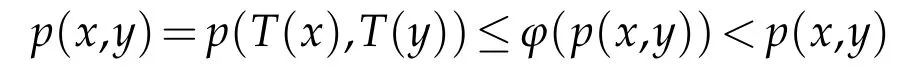
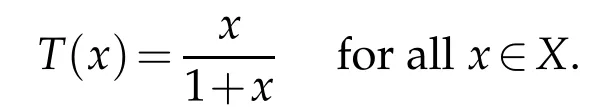
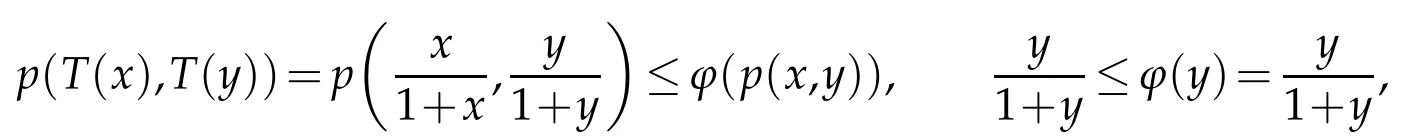
4 An application





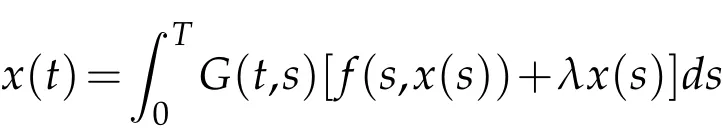

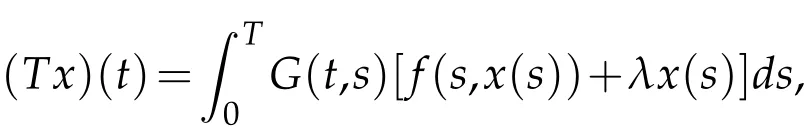

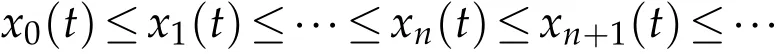
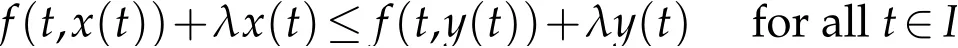












 Journal of Partial Differential Equations2021年1期
Journal of Partial Differential Equations2021年1期
- Journal of Partial Differential Equations的其它文章
- Lower Bound Estimate of Blow Up Time for the Porous Medium Equations under Dirichlet and Neumann Boundary Conditions
- Finite-Time Blow-Up and Local Existence for Chemotaxis System with a General Memory Term
- The Averaging Principle for Stochastic Fractional Partial Differential Equations with Fractional Noises
- Remarks on Blow-Up Phenomena in p-Laplacian Heat Equation with Inhomogeneous Nonlinearity
- On Free Boundary Problem for the Non-Newtonian Shear Thickening Fluids
- Global Existence of Smooth Solutions to Three Dimensional Hall-MHD System with Mixed Partial Viscosity
