城轨车辆杆的弹性模量实验研究
——以特殊截面为例
陈玲
(苏州建设交通高等职业技术学校,江苏苏州 215104)
1 杆的研究意义
杆作为悬挂的支撑部件,是机械零部件中非常重要的一个元素,其在轨道车辆上杆部件也是很多,发挥着不可或缺的作用。杆的材质并不是单一的,更多是多种材料复合而成。对于杆的力学的弹性模量需要通过实验取得。因此,对试验求取的不同截面和材质的杆的弹性模量,选取合适的罗马杆有重要的现实意义和经济价值。同时对罗马杆进行研究,可进一步了解城轨车辆上杆。
2 市场调研
走访多个装饰市场,经营罗马杆的商家,市场调研了很多种罗马杆,有不同材质和不同截面的罗马杆。调研统计了解到罗马杆的主要种类如图1所示。此前已经进行了普通截面的研究,本文此处作关于特殊截面加强型的罗马杆的力学研究。

图1 普通型和加强型罗马杆
3 三点弯曲实验求杆弹性模量
市场调研的罗马杆的材质,不是单一材质而成的,是由多种材质复合而成的,各材料的弹性常数是未知的,为此,需要通过实验测得罗马杆的弹性模量
(1)三点弯曲理论。长为L 的简支梁AB,中间受集中载荷F作用。根据《材料力学》[1]知其中比值K 可通过三点弯曲实验得到。一旦比值K 已知,就可得到弹性模量。
(2)三点弯曲实验。根据市场调研情况及购置的实物样本,选取两种具有代表性特殊截面的罗马杆进行试验,测得它们的弹性模量。利用长春试验机研究所有限公司的100kN 电子万能试验机进行实验,实验装置如图2所示,弯曲实验的标距L=600mm。

图2 三点弯曲实验装置
(3)梅花形杆。图3为铝合金梅花形截面杆。其梅花形截面可近似看成12 边形,测得几何尺寸为:
外径D2=26.875mm,边长b=7.201mm,厚度δ=1.107mm。
内径D1=D2-2δ=26.875-2×1.107=24.661mm,横截面积近似为十二个小矩形的面积之和:A=12×7.201×1.107×10-6=9.5658×10-5m2。
下面计算截面关于z 轴的惯性矩。截面由12 个矩形组成,所以先给出矩形在任意位置时的惯性矩,如图4所示。设矩形的长为b,宽为h=δ,则由不同轴惯性矩之间的关系可得[1]:
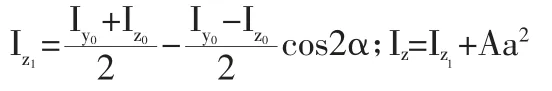
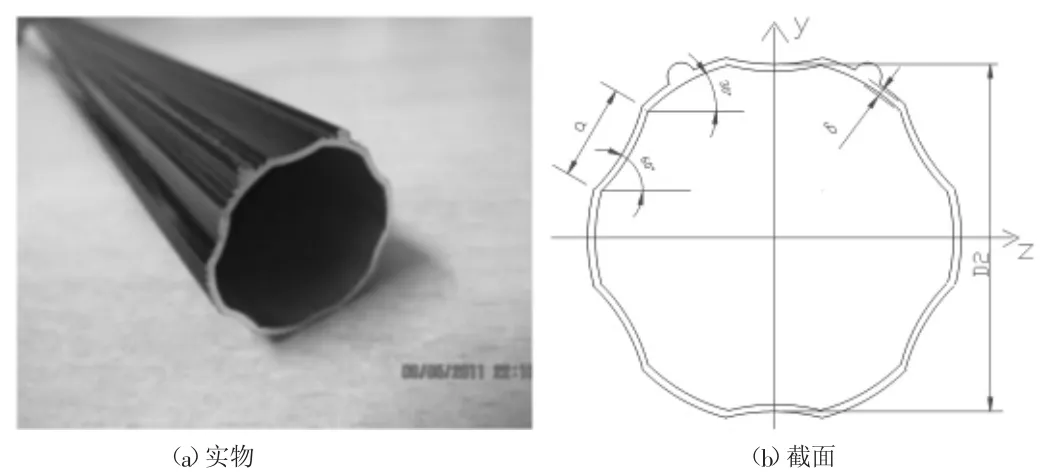
图3 梅花形杆

图4 惯性矩转轴
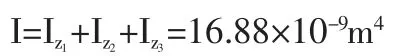
因此,由12 个矩形组成的梅花形截面总惯性矩为:

由三点弯曲实验得到力-位移曲线如图5所示。选取比例极限范围内合适的两点算出:K=595980N/m,由此算出杆的整体弹性模量E=302.80GPa。
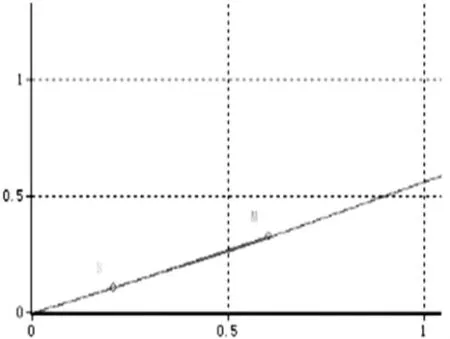
图5 梅花形杆力-位移曲线
(4)Y 形加强杆。如图6(a)所示为Y 形加强杆,杆的横截面分为三部分:外圈为薄壁圆杆,内部的上半部分为两个薄壁圆弧(四分之一圆)和下半部分为一个矩形。测得几何尺寸为:
外径D=29.900mm,3 处的壁厚分别为δ1=0.880mm,δ2=0.940mm,δ3=1.287mm。则内圆弧的内径为d1=D-2δ1=28.140mm,外圆的内径为d2=D-2δ3=27.326mm。
计算出横截面各部分的面积及总面积为:

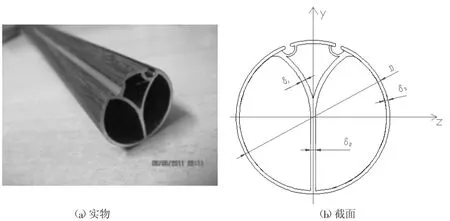
图6 Y 形加强杆
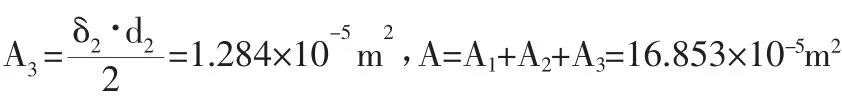
计算出截面惯性矩:

三点弯曲试验力-位移曲线如图7所示。选取比例极限范围内合适的两点算出:
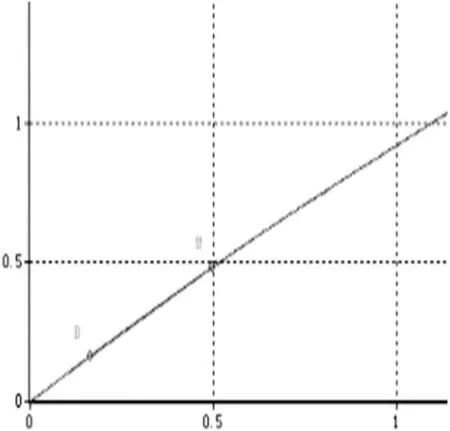
图7 Y 形杆力-位移曲线
K=947321N/m,由此算出杆的整体弹性模量E=252.54GPa。

表1 两种样品数据比较
4 结语
由以上可知,特殊截面的杆的弹性模量用试验取得过程中,其横截面不同计算的惯性矩方法不一样,可分割、类似组合而成。弹性模量只与材质有关,与其他参数无关,铝合金价位合理经济适用,因此我们首选罗马杆材质为铝合金。

