基于数字图像相关方法的裂隙砂岩应变场演化规律及前兆识别

张 科，李 娜

（1.昆明理工大学电力工程学院，云南 昆明 650500；2.昆明理工大学建筑工程学院，云南 昆明 650500）

裂隙岩体是工程建设中广泛遇到的工程介质，受荷条件下裂隙岩体的力学特性是影响工程安全与稳定的重要地质条件[1-4]。为更准确地研究岩体的真实特性[5]，一些学者直接采用含预制裂隙的岩石材料进行试验研究。Wong等[6]和曹平等[7]系统地总结了单轴压缩作用下单裂隙岩石试件的裂纹萌生、扩展及贯通规律。杨圣奇等[8]和Huang等[9]研究了预制裂隙几何参数对双裂隙岩石试件强度与变形破裂特征的影响效应，认为试件破坏模式主要表现为拉贯通、压贯通、剪贯通和混合贯通。赵洪辉等[10]分析了共面裂隙群砂岩试件的压缩变形破坏规律。

近年来，数字图像相关（Digital Image Correlation，DIC）方法在实时追踪岩石全场变形方面得到了尝试与发展，该方法最早由日本学者Yamagughi[11]和美国学者Peter等[12]于20世纪80年代初提出。马少鹏[13]和宋义敏等[14]以DIC技术为观测手段，计算得到了完整岩石试件在压缩加载过程中的全场变形信息，分析了岩石变形破坏过程中的应变局部化现象。徐金明等[15]利用DIC技术和试验视频获得了石灰岩压缩试验中的位移场变化规律。潘红宇等[16]研究了单轴压缩作用下奥陶系沉积岩石中裂纹周围的应变率与裂纹扩展之间的关系。大久保诚介等[17]和Tang等[18]通过三维DIC技术计算岩石试件破坏过程中的三维位移场和应变场，认为应变场演化能够反映裂纹萌生、扩展及贯通规律。袁媛等[19]结合DIC技术，定量研究了单轴压缩破坏过程中含填充预制裂隙的大理岩试件位移场和应变场演化特征。

上述试验研究侧重于通过DIC技术得到岩石破坏过程的变形场云图，但缺乏对变形场数据进行定量分析。若能将DIC技术与一些量化指标相结合，则可以更直观、更准确地把握裂隙岩体变形场动态演化规律。基于此，本文采用DIC方法计算得到单轴压缩加载过程中裂隙砂岩试件应变场，引入方差和分异速率两种指标对应变场及应变局部化带演化特征进行定量分析；结合应变场分异速率变化规律，研究了岩体失稳的前兆特征。

1 DIC基本原理

DIC方法是一种环境适应性强、测量精度高的非接触式光学测量方法[14-19]。其基本原理如图1所示，通过比较试件变形前后的数字散斑图像，追踪以点O（x0,y0）为中心的子区f1，通过相关匹配找到变形后以点O′（x0′,y0′）为中心的子区f2。对于该子区内，变形后P′（x′,y′）与变形前P（x,y）之间的关系[20]为：

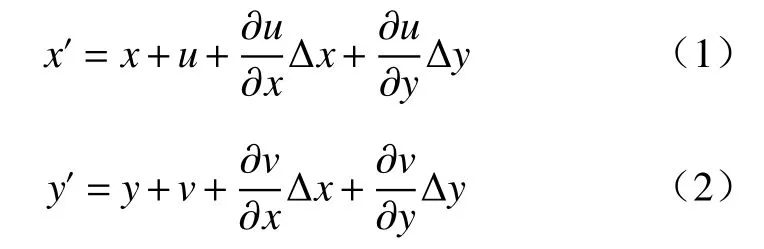
式中：u、v——变形前后子区中心点在x、y方向上的位移分量；

Δx、Δy——点O到点P在x、y方向上的距离；

重复以上过程，得到试件表面的全场变形信息。

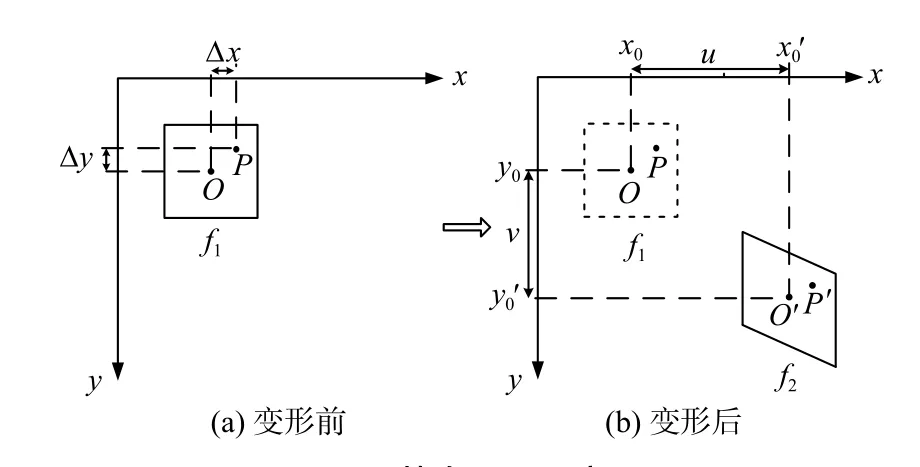
图1 基本原理示意图Fig.1 Schematic diagram of the basic principle

2 试件制备及试验方法

2.1 试件制备

试验所用岩样为取自云南省昆明市地区的红砂岩。将岩块进行切割、打磨处理，加工成尺寸为120mm×60mm×20mm（长×宽×厚）的岩板试件。采用高速水刀技术切割形成单裂隙砂岩试件，裂隙中心与试件几何中心重合，裂隙长度（2a）为 20mm，裂隙倾角（β）考虑30°、45°、60°三种工况，裂隙内部填充云母片。最后，对试件正面喷涂白漆和黑漆形成均匀、随机的人工散斑场[19]。试件示意图如图2所示。

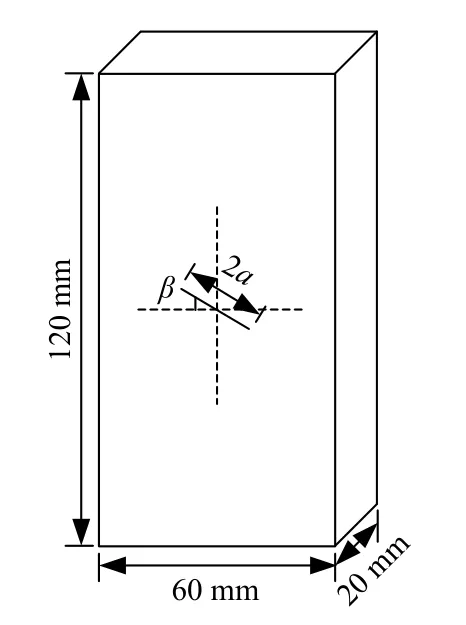
图2 试件示意图Fig.2 Schematic diagram of specimen

2.2 试验设备及试验过程

采用WDW-100E微机控制万能材料试验机进行单轴压缩试验，加载方式为位移控制，加载速率设置为0.005mm/s。采用分辨率为2 592×1 944 像素的工业相机实时采集试验过程中试件表面的散斑图像，采集速率设置为1 张/s。同时，在工业相机旁放置LED光源，为数字散斑图像采集提供稳定的光源。

3 试验结果与分析

不同裂隙倾角的砂岩试件轴向应力-应变曲线如图3所示。以加载前的数字散斑图像为参考，采用数字图像相关处理软件Ncorr对采集的数字散斑图像进行相关运算得到位移场，而后再进行数值微分，得到加载全过程的水平应变场εxx、垂直应变场εyy以及剪应变场γxy云图。研究发现不同裂隙倾角的砂岩试件应变场演化过程大致相似，限于篇幅，仅对30°裂隙倾角的试件进行应变场演化特征分析。图3中各标识点分别对应不同的应力加载水平：标识点1处于加载初期，标识点2处于弹性变形初期，标识点3处于新生裂纹萌生状态，标识点4处于剪切裂纹出现状态，标识点5处于裂纹快速扩展状态，标识点6处于最终破裂状态。图4—图7为30°裂隙倾角砂岩试件加载过程各标识点所对应的裂纹扩展、水平应变场、垂直应变场以及剪应变场云图。

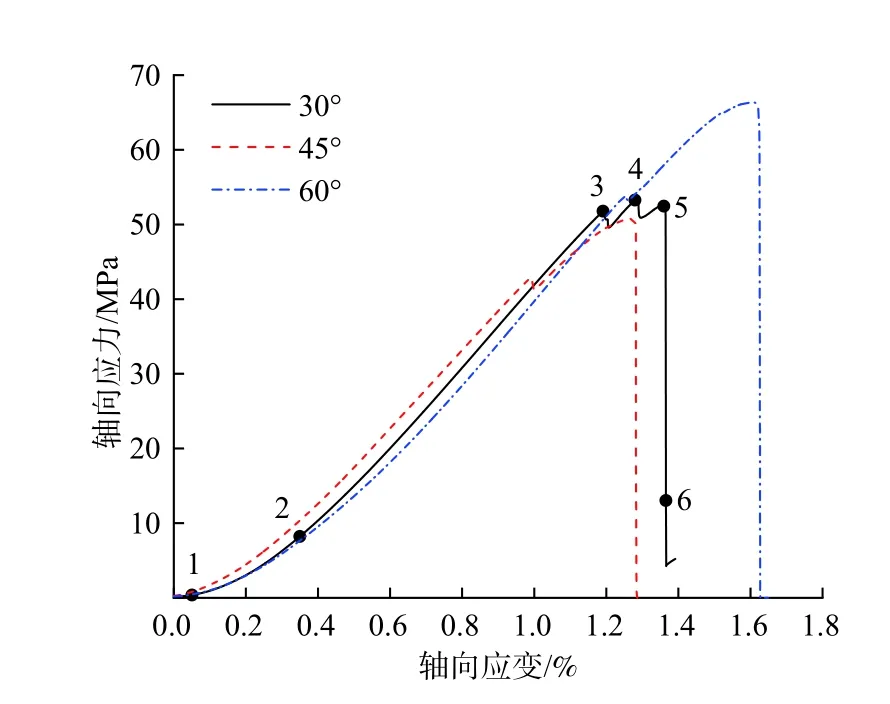
图3 应力-应变曲线Fig.3 Stress-strain curves

结合应力-应变曲线以及变形破裂特征，裂隙砂岩应变场演化过程大致可以划分为如下阶段：

（1）压密阶段（标识点1、2）：试验加载初期，试件内部微孔隙、微裂隙受压闭合，应力-应变曲线稍微向上弯曲；从图5（a）—图7（a）中标识点1对应的应变场云图可以看出，此时应变场分布较均匀，数值非常小。

图4 30°裂隙倾角试件加载过程裂纹扩展Fig.4 Crack propagations during loading process with flaw inclination of 30°

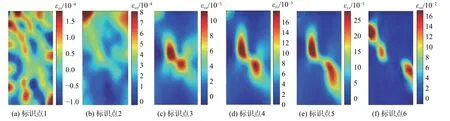
图5 30°裂隙倾角试件水平应变场演化Fig.5 Evolution of horizontal strain field of specimen with flaw inclination of 30°

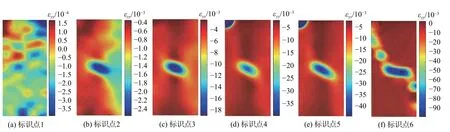
图6 30°裂隙倾角试件垂直应变场演化Fig.6 Evolution of vertical strain field of specimen with flaw inclination of 30°

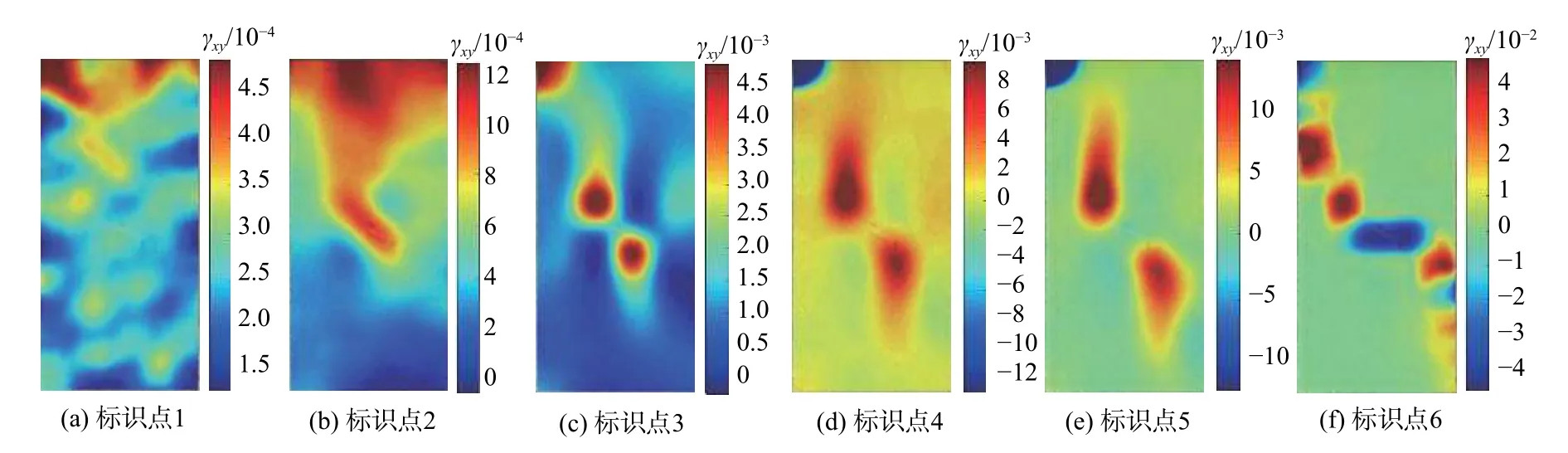
图7 30°裂隙倾角试件剪应变场演化Fig.7 Evolution of shear strain field of specimen with flaw inclination of 30°

（2）弹性变形阶段（标识点2、3）：随着荷载的增加，应力-应变曲线接近于直线，试件处于弹性变形阶段；从图5（b）—图7（b）中标记点2对应的应变场云图可以看出，此时应变场分布不再均匀，其中垂直应变场和剪应变场云图在预制裂隙周边开始出现应变局部化带。

（3）裂纹稳定扩展阶段（标识点3、4）：当加载至标识点3，预制裂隙尖端出现宏观张拉裂纹；从图5（c）—图7（c）中标识点3对应的应变场云图可以看出，此时预制裂隙及新生裂纹周围出现明显的应变局部化带。随着轴向荷载逐渐增加，张拉裂纹和相应的应变局部化带均沿着最大主应力方向稳定扩展。

（4）裂纹快速扩展及破坏阶段（标识点4、5、6）：当加载至标识点4，从图5（d）—图7（d）中可以看出，张拉裂纹相应的应变局部化带扩展停止。继续加载，预制裂纹尖端产生剪切裂纹，应变场云图的相应位置处出现应变局部化带，并向对角方向快速扩展，见图4（e）—图7（e）。最后，从图4（f）—图7（f）中标识点6对应的裂纹贯通和应变场云图可以看出，试件发生对角剪切破坏。

通过对比裂纹扩展路径和应变场云图可知，裂隙岩体变形破裂过程中的应变局部化带发展能够较好地反映裂纹起裂、扩展及贯通规律。因此，应变局部化带可用于判断岩体内部裂纹扩展情况。

4 基于应变场演化规律的前兆识别

为量化描述裂隙岩体加载过程中应变局部化现象，对应变场进行方差分析，其计算公式[21]如下：

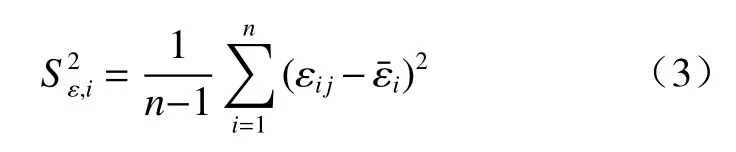
n——应变场子区总数；

εij——第i张散斑图像中第j个子区的应变值；

研究发现，方差可以描述裂隙岩体加载过程中应变局部化发展程度。对于不同裂隙倾角的砂岩试件，单轴压缩过程中3种应变场方差均表现出类似的演化规律。图8给出了30°裂隙砂岩试件的3种应变场方差-轴向应变曲线，可大致划分为3个阶段：

（1）稳定分异阶段（第Ⅰ阶段，标识点1、2、3）：该阶段持续时间最长，约占加载全过程的87%，对应于压密和弹性变形阶段；此时3种应变场方差小于0.01‰，且变化较小，说明应变分布较均匀，应变局部化现象不明显。

（2）加速分异阶段（第Ⅱ阶段，标识点3、4）：对应于裂纹稳定扩展阶段；此时3种应变场方差表现为加速上升，这是由于张拉裂纹的萌生和稳定扩展，在应变场上表现为应变局部化带范围逐渐扩大，导致应变场分异逐渐显著。

（3）加加速分异阶段（第Ⅲ阶段，标识点4、5、6）：对应于裂纹快速扩展及破坏阶段，加载应力达到峰值后，产生剪切裂纹；相比于张拉裂纹，剪切裂纹扩展是一个更快且不稳定的过程[22]，导致应变局部化带发展也更快，所以应变场方差呈现出增长加快的趋势，以垂直应变场方差-轴向应变曲线最为明显。

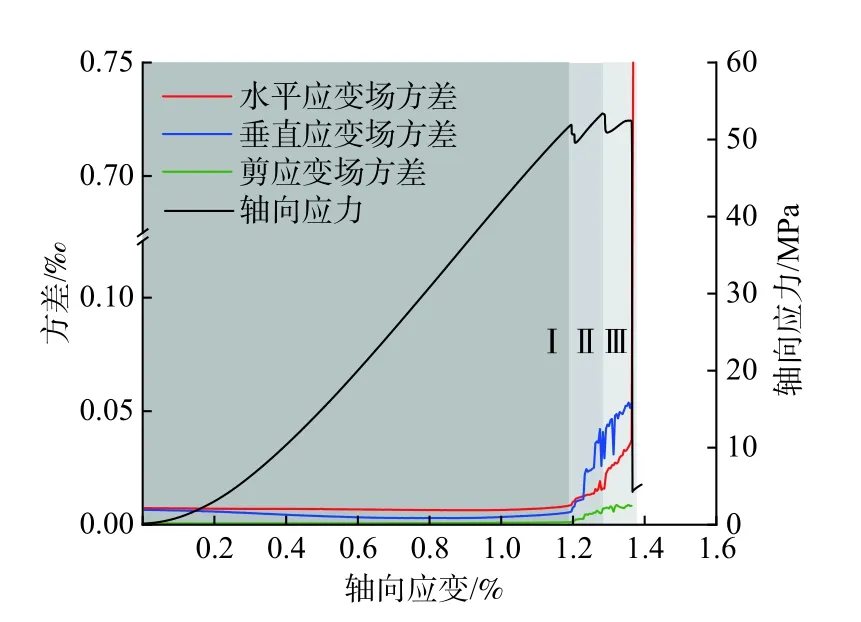
图8 应变场方差-轴向应变曲线Fig.8 Variance of strain field-axial strain curves

从图8可以看出，加载过程中应变场方差曲线均表现出阶段性的变化特征。为更准确地衡量这类规律，对应变场方差-轴向应变曲线进行有限差分求导，计算得到应变场分异速率[23]：

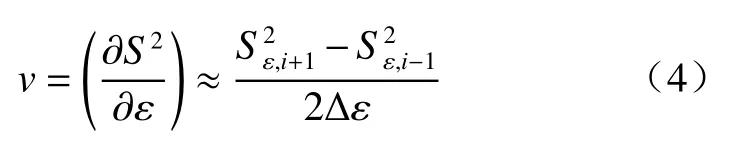
式中：∆ε——相邻散斑图像之间的应变增量。

通过研究发现，对于不同的裂隙倾角，砂岩试件应变场分异速率变化曲线表现出不同的形态，即具有不同的应变场分异特征。但是，所有试件的3种应变场分异速率-轴向应变曲线在张拉裂纹起裂时均会出现第一个尖峰，记为前兆点P。限于篇幅，仅对30°裂隙倾角试件的分异速率-轴向应变曲线做出分析。如图9所示，前兆点P的出现明显将应变场分异速率变化曲线分成了两部分：

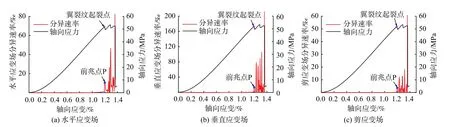
图9 30°裂隙倾角试件应变场分异速率-轴向应变曲线Fig.9 Differentiation rate of strain field-axial strain curves of specimen with flaw inclination of 30°

（1）前兆点出现之前，由于轴向荷载的增加，应变数值虽然逐渐增大，但是此阶段的试件处于压密和弹性变形阶段，所以应变场方差基本保持不变，由此造成应变场分异速率基本为0。

（2）前兆点出现之后，由于试件内部形成宏观裂纹，打破了原有的应变场和应变场平衡，应变场方差产生突增，在应变场分异速率-轴向应变曲线表现为第一个尖峰。此后，裂纹扩展导致分异速率变大，也有可能再次出现尖峰。

从图9可知，对于同一试件，3种应变场分异速率-轴向应变曲线相应的前兆应力都一致。统计30°、45°、60°裂隙倾角试件的前兆应力与峰值应力比，其数值分别为0.96，0.81，0.80。因此，对于不同裂隙倾角的3种应变场分异速率变化曲线，前兆点P的出现均可作为裂隙岩体即将失稳的前兆信号。需要指出的是，本文旨在通过应变场分异速率-轴向应变曲线，提出一种识别裂隙岩体失稳破坏前兆信号的方法，而影响分异特征及前兆应力的因素多且复杂，如裂隙倾角、岩石类型、矿物成分等。相关结果还需要考虑上述因素的影响，进一步开展试验进行充分的验证。

5 结论

（1）宏观裂纹的萌生、扩展以及贯通引起应变局部化带的扩展延伸，通过分析裂隙砂岩试件加载过程中水平应变场、垂直应变场以及剪应变场云图及其应变局部化带的变化，试件变形破裂过程大致可划分为压密、弹性变形、裂纹稳定扩展、裂纹快速扩展及破坏阶段。

（2）应变场方差-轴向应变曲线大致可划分为稳定分异、加速分异以及加加速分异等3个阶段，分别对应压密和弹性变形、裂纹稳定扩展、裂纹快速扩展及破坏阶段。加载过程中应变场方差的变化与裂纹萌生、扩展以及贯通密切相关。

（3）张拉裂纹首次出现时，岩体内部结构发生变化，引起应变场方差突增，导致应变场分异速率-轴向应变曲线出现第一个尖峰，可作为裂隙岩体失稳预警的前兆点，对应的前兆应力与峰值应力比值为0.80～0.96。本文提出的前兆识别方法可为工程岩体失稳预测提供一定的理论参考。