Wave–particle duality relation with a quantum N-path beamsplitter*
Dong-Yang Wang(王冬阳), Jun-Jie Wu(吴俊杰),†, Yi-Zhi Wang(王易之), Yong Liu(刘雍),2,An-Qi Huang(黄安琪), Chun-Lin Yu(于春霖), and Xue-Jun Yang(杨学军)
1Institute for Quantum Information&State Key Laboratory of High Performance Computing,College of Computer Science and Technology,National University of Defense Technology,Changsha 410073,China
2College of Information and Communication,National University of Defense Technology,Xi’an 710006,China
3China Greatwall Quantum Laboratory,China Greatwall Technology Group CO.,LTD.,Changsha 410073,China
Keywords: wave–particle duality,interference visibility,path distinguishability,quantum N-path beamsplitter
1. Introduction
Bohr’s principle of complementarity[1,2]indicates that a quanton may possess various properties,and depending on the exclusive detecting devices, we will observe one of the corresponding behaviours. Wave–particle duality,[3]which considers a quanton’s behaviour in a two-path interferometer, is the most famous instance. If we choose to detect along which path the quanton propagates, in order to obtain information from its particle property, no interference visibility as information from its wave property is extractable, and vice versa.This can be understood more easily by a Mach–Zehnder interferometer (MZI), with presence or absence of the second beamsplitter(BS)to reveal the photon’s wave or particle property respectively.[4]Because these two cases are incompatible,appearance of one behaviour suppresses that of the other,and complete wave and particle properties can never be observed simultaneously. The general relation between them is described by the inequality derived by Englert,[5]expressed as

where V is the interference visibility and D is the path distinguishability. It considers the intermediate situation where incomplete wavelike and particlelike behaviours are revealed,and sets a limitation on the amount of the total extractable information from wave and particle properties. Experiments with different kinds of quanton have verified this inequality.[4,6–9]
Surprisingly, previous studies demonstrated that the introduction of a quantum BS(QBS)[10–13]broke the limitation set by Eq. (1).[14]This occurs because as the QBS is in the superposition between presence and absence, it is entangled with wave and particle states of the quanton. When it collapses on a certain state, wave and particle states are enabled to be superimposed,[15]and interference between them causes the break.
On the other side, it is not natural to generalize the inequality of Eq.(1)to N-path case,[16,17]because dispute exists on finding an operational measure of how much wave property is observed. According to studies on N-path interference,visibility and path distinguishability are not complementary in some situations,and V is argued not to be a good measure for wave property.[18–20]Efforts have been made to handle with this issue.[21–29]In Ref.[30], the averaged visibility and path distinguishability are considered in all N(N −1)/2 two-path interferences,and are derived

where Vmnis the visibility of interference between paths m and n, and DQmnis the success probability in unambiguous quantum state discrimination(UQSD)[31–34]between the corresponding which-path detector(WPD)states.
However,it is unclear whether a generalized QBS is able to break the limitation set by Eq.(2)in N-path interference. In this paper, we use quantum Fourier transform[35]as a N-path BS(BSN),and propose a model of N-path interferometer with a quantum BSN(QBSN). We study relation between the averaged visibility and path distinguishability, and find similar phenomena that the limitation in Eq.(2)is broken,but not for all detection ports. We further analyze the case where wave property partially interferes with particle property, and provide a quantitative description of the relation between wave property’s interference with particle property and the maximal extractable information from these two properties. We then propose an implementation of a N-path interferometer with a QBSN,and an experiment methodology to verify the break of the limitation. Our work exhibits the effect of quantum superposition on wave and particle duality, which provides a new aspect of the relation between visibility and path distinguishability in N-path interference.
2. Theoretical analysis
2.1. Duality relation with a QBS
In this part, we recap the break of the duality relation in Eq.(1),with a QBS introduced.[11]The whole system consists of the photon system (labeled as s) and the QBS system (labeled as c). When the photon enters the two-path MZI shown in Fig.1(a),absence of the QBS makes the combined system in the state|absence〉c|p〉s,where

When the QBS system finally collapses on cosα|absence〉c+sinα|presence〉c, the photon system becomes in a superposition between wave and particle states

with the normalization factor
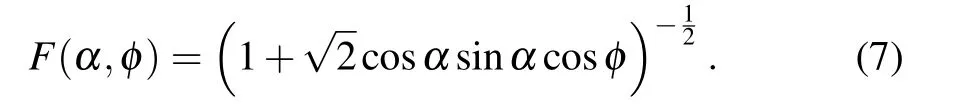
It is notable that, |p〉sand |w〉sgenerally are not orthogonal,and the normalization factor depends on α and phase φ.

For a photon in a two-path interferometer, |0〉sand |1〉sare two possible states for it to propagate along the two paths.When the photon is in the quantum superposition between|0〉sand |1〉s, the interference between the two paths causes the constructive or destructive output intensity. For a photon in the state|ψ〉s,|p〉sand|w〉sare also two possible states that it may stay in,and can also be regarded as two possible“paths”where the photon may “propagate” in a fictitious interferometer. The interference between these two “paths” (i.e. |p〉sand|w〉s)causes the constructive or destructive output“intensity”(i.e. V2and D2)similarly,and for the constructive cases Eq.(1)may be broken.
To explain this in detail, we consider extractable information of |ψ〉sfrom wave and particle properties in Eq. (1).Since the QBS is asymmetric for most cases, different detection ports should be treated separately.[36]For port 0,the output intensity is proportional to


2.2. Different ways to obtain the photon’s path information
In the original derivation of the duality relation of Eq.(1),the authors considered entanglement between the photon and the WPD system,and the interferometer consists of two symmetric BSs.[5]The photon’s path information is revealed by discrimination between the corresponding states of WPD.Later in Refs. [4,36], the authors pointed out that, the path distinguishability D in Eq. (1) could also be introduced by an asymmetric output BS, which differs from the case where the input BS is asymmetric,and path predictability rather than path distinguishability is offered.[4]In this subsection,we will show that,though path distinguishability is considered in different setups and appears to be in different forms, it has the same meaning — “the measure of how much better one can do by using prior information and detectors than by just random guessing”.[25]


In our following analysis,as a generalization of Ref.[11],we consider a N-path interferometer with a QBSNand study Eq.(2)in such a configuration. For each two-path interference by path m and n,we adopt the operational definition of Dmnin the asymmetric interferometer, and convert it to DQmnby the relation between them. This is sensible according to the above explanation.
2.3. An interferometer with quantum N-path beamsplitter
In Fig. 1(b), we propose our N-path interferometer with a QBSN. The first BSNgenerates a symmetric superposition among N paths. To investigate the limitation set by Eq. (2),each time we select two of the N paths and block the others.With presence of the second BSN, path character of the detected photon is indistinguishable,and no information from its particle property is extractable. In contrast, full information from wave property is obtained by interference visibility of the output intensity, which equals to 1. While in the absence case, full information from particle property is obtained, but the output intensity stays at a constant with varying φ. When a QBSNis in the intermediate situation,wave and particle states are superimposed,and part of the information from each property is extractable.


where Re represents the real part of a complex number. The three terms summed up in Eq.(15)correspond to the contribution of particle state,wave state,and the interference between them to the output respectively. The visibility for path m and n is derived from Eq.(9). An average over all N(N −1)/2 pairs gives Vk(α)as the extractable information from wave property of the input photon.
DQk(α)can be obtained similarly with the two-path case.For the photon detected at port k,the probability of it coming from path l=m or n is
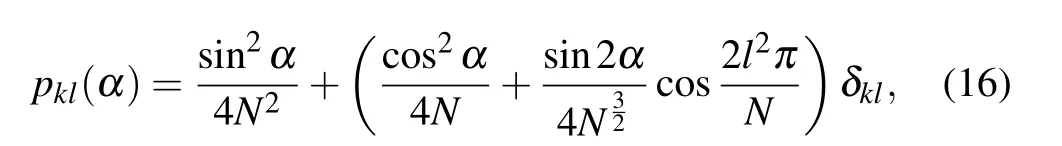
where δklequals to 1 if k=l and 0 otherwise. Extractable information from particle property is expressed as DQk,mn(α)=
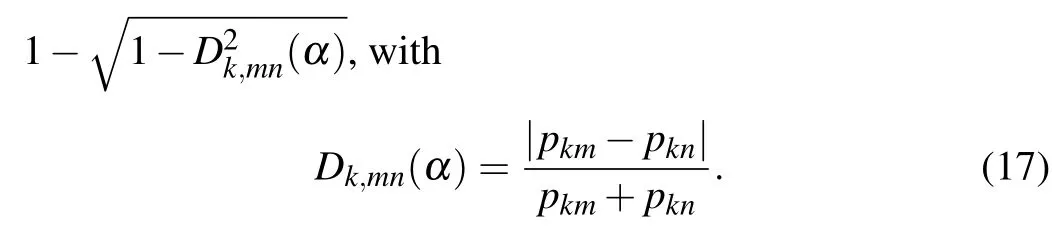
2.4. Deriving break of the limitation
In this subsection, we fix the detection port at k=0 for convenience. A more general case will be discussed later. We divide all the pairs into two parts. The first part corresponds to N −1 pairs containing path 0, namely (0,n). We derive visibility



2.5. A more general case when k/=0
For a more general case where port k/=0,we calculated V′k(α)and D′Qk(α)for the first part,i.e.pairs containing path k, as quantities for the second part are the same with those when k=0. We exhibit derivation of visibility and path distinguishability for the cases(k,n >k),and cases of the counterpart(m,k >m)are handled similarly.
Starting from Eqs.(14)and(15),we have



Fig. 3. Results of further calculations. (a)V′k+D′Qk with different k when N=6. The case for detection port k is identical to that for N −k,due to the periodicity of each element in quantum Fourier transform.Break of the limitation corresponds to the situation when k2/N =0 or 3/2. (b)V0+DQ0 with different p when N =2. (c)A quantitative relation between the maximum of V0+DQ0 and p,with N varied from 2 to 7. As p decreases, the maximum drops dramatically. The minimal value of p that makes the violation for each N is 0.825, 0.867, 0.887,0.910,0.928 and 0.938 respectively.
2.6. Quantitative analysis of wave–particle interference’s effect
We further analyze the interference between wave and particle properties in this model, and provide a quantitative relation between the maximum of Vk+DQkand the interference. In Eq. (15), not only output intensity of the wave part,but also that of the interference between the wave part and particle part,oscillate with φmn. The difference between their phases is 2k2π/N,for k=m or n.Both wave state and interference between wave and particle states give information from wave property. The break occurs when 2k2π/N =zπ, which indicates the enhancement on the oscillation of|wmn〉sby that of the interference between|pmn〉sand|wmn〉s.
To quantitatively analyze the wave–particle superposition’s effect on the violation of Eq.(2),we consider a QBSNin partial quantum superposition of |absence〉cand |presence〉c,which can be realized by initializing the controlling system in Fig.1(c)as

where parameter p represents the coherence of ρc. Consequently, in the interference between path m and n, the photon is in the partial quantum superposition between wave and particle states,
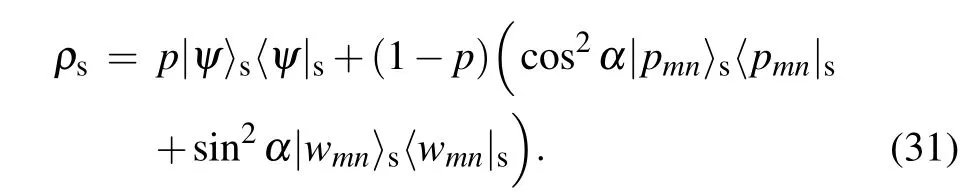
The parameter p quantifies the quantum superposition between wave and particle properties. A straightforward deduction indicates the result is to replace all the sin2α terms in the previous representations by psin2α, and it makes no difference for pairs that does not contain path k. For convenience,we fix the detection port k at 0.The result for N=2 is shown in Fig.3(b),and α0that makes maximum of V0+DQ0decreases as p gets smaller. In Fig. 3(c), we exhibit the maximum of V0+DQ0’s reliance on p with N varied from 2 to 7, and the maximum decreases dramatically as p gets smaller and finally stays at a constant of 1. As N gets larger, the maximum decreases faster with p. Theoretically, cases for all values of N and k can be calculated,and a general quantitative description of wave–particle interference’s effect on the break of the limitation is available.
3. An optical scheme of the N-path interferometer with a QBSN



4. Discussion
4.1. Observer’s influence on visibility and path distinguishability
As a further explanation, we point out here that the break of the limitation and the interference between |pmn〉sand |wmn〉sare the consequence of loss of detection, which is caused by postselection from the view of observers. We explain this by a two-path MZI,and cases for N-path interference can be generalized similarly.
The general description of a BS is a unitary transformation

Presence and absence of a symmetric BS give R=1/2 and R=1 respectively, which corresponds to minimal and maximal path distinguishability. When we consider a QBS and postselect the controlling system with |α〉c=cosα|0〉c+sinα|1〉c,we actually make a transformation as
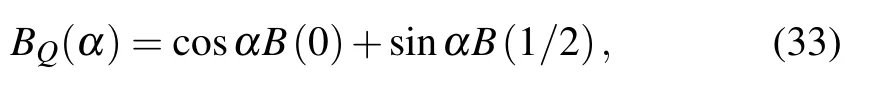
which is non-unitary and causes losses.
As we make postselection, cases where the controlling system collapses on the orthogonal state|α⊥〉care discarded.The observed phenomenon orients from an incomplete detection. If we supplement the discarded information from|α⊥〉c,there will be no loss of information, and the inequality still holds. This corresponds to the case where we detect the photon regardless of state of the controlling system. Thus, the break occurs as if we subjectively pick part of the observation and make an artificial interference between wave and particle properties. A similar point of view is indicated in Ref.[10].
4.2. Comparison with previous similar studies
In Refs. [45,46], it was pointed out that the loss in MZI could cause the break of the limitation,and loss indeed exists in the interferometer with a QBS(or QBSN)when postselection is conducted. However,as discussed below,although the breaks of Eq. (1) in both models are related with the loss in the interferometer,they are not equivalent,and the model proposed in those studies can not generate the quantum superposition between wave and particle states.
Similar to Subsection 4.1,the loss in Refs.[45,46]can be represented by the non-unitary matrix as
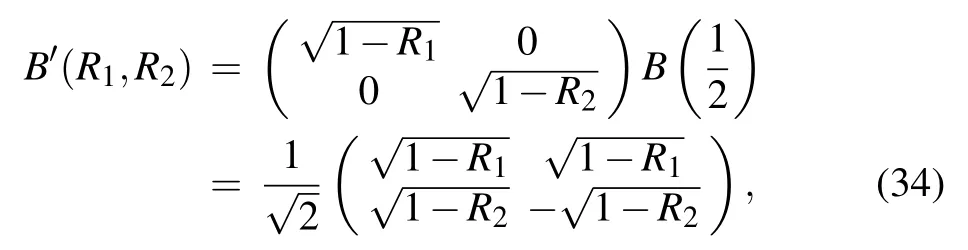
where R1and R2are reflectivities of the two beamsplitters after the standard MZI and represent the losses.Since B′(R1,R2)and BQ(α) are different except for the case where cosα =0 and R1=R2=0 which corresponds to a lossless MZI, these two models are generally not equivalent. The former model with two additional beamsplitters can not be used to study the effect of the interference between wave and particle states on the duality relation. Besides, as mentioned in Ref. [45], the loss in their model has no effect on the visibility. However,in the model of a QBS (or QBSN), both the visibility and path distinguishability are affected,which is exhibited in Fig.2.
4.3. Wave–particle duality with a quantum WPD[47]


5. Conclusion
In conclusion,we study the extractable information from wave and particle properties in N-path interference, with a QBSNin the quantum superposition between presence and absence. The consequent interference between wave and particle states of the quanton causes summation of averaged visibility and path distinguishability to break the limitation of 1.Through a quantitative analysis, we find that the maximum of V+DQdecreases dramatically, when wave property interferes with particle property partially. As N getters larger, the maximum decreases faster. We then propose a scheme to experimentally verify our analysis. Our work exhibits the effect of quantum superposition on wave–particle duality, and provides a new aspect of relation between visibility and path distinguishability in N-path interference.
- Chinese Physics B的其它文章
- Corrosion behavior of high-level waste container materials Ti and Ti–Pd alloy under long-term gamma irradiation in Beishan groundwater*
- Degradation of β-Ga2O3 Schottky barrier diode under swift heavy ion irradiation*
- Influence of temperature and alloying elements on the threshold displacement energies in concentrated Ni–Fe–Cr alloys*
- Cathodic shift of onset potential on TiO2 nanorod arrays with significantly enhanced visible light photoactivity via nitrogen/cobalt co-implantation*
- Review on ionization and quenching mechanisms of Trichel pulse*
- Thermally induced band hybridization in bilayer-bilayer MoS2/WS2 heterostructure∗

