液压支架的调直方法研究*

王宇卓,常宗旭,高 飞,廉自生

(太原理工大学 机械与运载工程学院,山西 太原 030024)

0 引 言

自动化综采工作面是以采煤机与液压支架联动为特征的工作面[1,2]。由于受到井下复杂的环境影响,并且在“推溜移架”过程中出现的测量误差和执行误差等,会导致工作面循环截割过程中存在误差不断累积,并在多次循环后需要人工干预,来满足综采工作面对于直线度的要求[3,4]。因此,实现综采工作面无人化的前提就是实现工作面的自动调直。

由于液压支架和刮板输送机的连接关系,使它们的直线度存在联系。因此,工作面自动调直方法分为:以液压支架为基准的调直方法和以刮板输送机为基准的调直方法。刮板输送机的调直方法是通过采煤机定位技术[5,6],由采煤机运行轨迹根据采煤机与刮板输送机的几何约束关系反演出具有绝对方位的刮板输送机轨迹[7-9]。也可在刮板输送机配置角度传感器[10]或者光纤光栅[11]求得刮板输送机轨迹;再通过调直算法计算各个液压支架所需的推移距离对刮板输送机轨迹进行修正。这种调直方法不但避免了误差累计,而且存在调直的绝对方向[12]。但是这种自动化技术较为复杂,其精度要求高;并且存在定位系统不可避免的漂移等误差,致使一段时间后定位效果无法满足工作需求,要进行人工干预[13,14]。

以液压支架为基准的调直方法是基于支架间的相对位置,来感知支架的相对位置(目前已提出了的方法有:找直和角度传感器[15]、激光列阵[16]、角度与应变[17]、视觉传感器[18]、井下机器人[19]等);之后在“拉架”过程中控制行程,使得支架两两对齐,也可以多架联动对齐;然后在以液压支架为基准推移刮板输送机,从而达到综采工作面调直的目的[20]。这种调直方法的优点是安装简单,可以直接在原有的支架上加装传感器实现,并且精度高成本低;缺点是大量传感器导致可靠性降低,存在误差累计,而且缺少绝对参考方向,极易导致工作面调直精度降低、调直方向与回采巷道方向不正交。

牛剑锋在内蒙古巴彦高勒煤矿进行了原理性实验,用精度为3 mm的激光对位传感器,达到直线度控制精度达到30 mm。

本文对以液压支架为基准的调直方法进行改进,并进行仿真实验和理论分析,通过对比分析测量误差和推移误差对直线度的影响规律。

1 以液压支架为基准的调直方法

笔者以液压支架为基准的调直方法通过激光列阵传感器来感知支架的相对位置。

工作面液压支架动态调节示意图如图1所示。

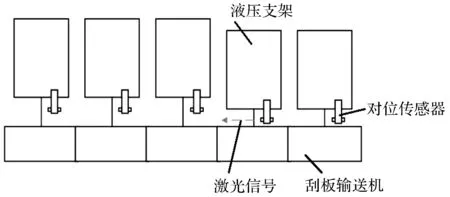
图1 液压支架动态调直示意图

所有液压支架都安装激光对位传感器。移架前对调斜量控制。准备移架的支架向相邻的支架发出命令,通知相邻的支架控制器发出激光信号。图1中箭头为对位传感器激光信号。移架中的支架可以接收信号,在激光信号接收列阵中感知与前一支架的相对位置;再在拉架过程中控制推移距离,从而实现支架运动的感知和控制,实现连续自主移架。

然而由于调直过程中存在精度和误差的问题,会导致偏离目标直线。为了补偿误差,用液压支架记录本次最终完成的行程目标与靶位的相对距离,其超出或不足的行程称为超调量,并使得相邻液压支架超调量相互抵消,最终保证支架移架行程误差控制在有效范围内。

单个液压支架具体控制流程图如图2所示。

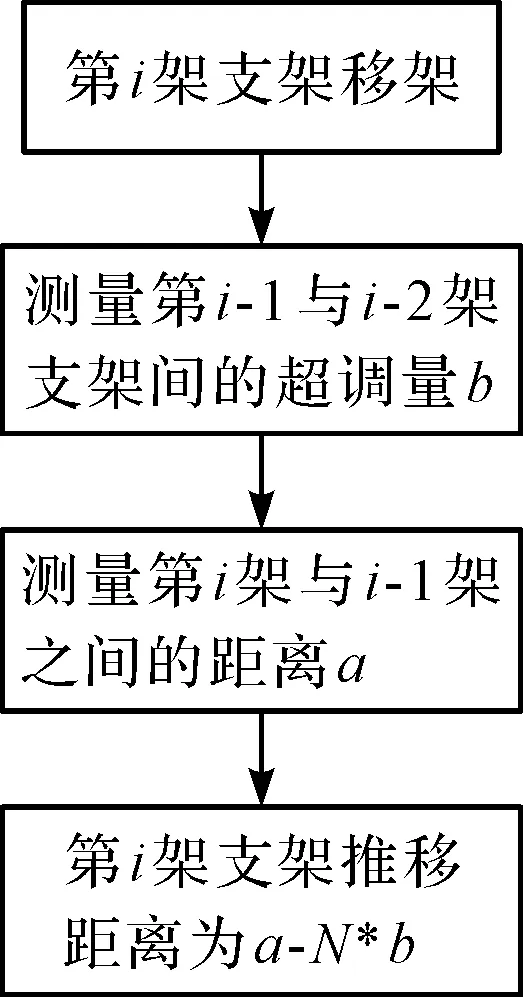
图2 液压支架动态调直流程图

根据液压支架调直方法,首先确定第1架第2架调直的纵坐标如下:

(1)

第i+1(i>1)座液压支架调直过程如下:

(2)

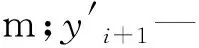
2 理论分析

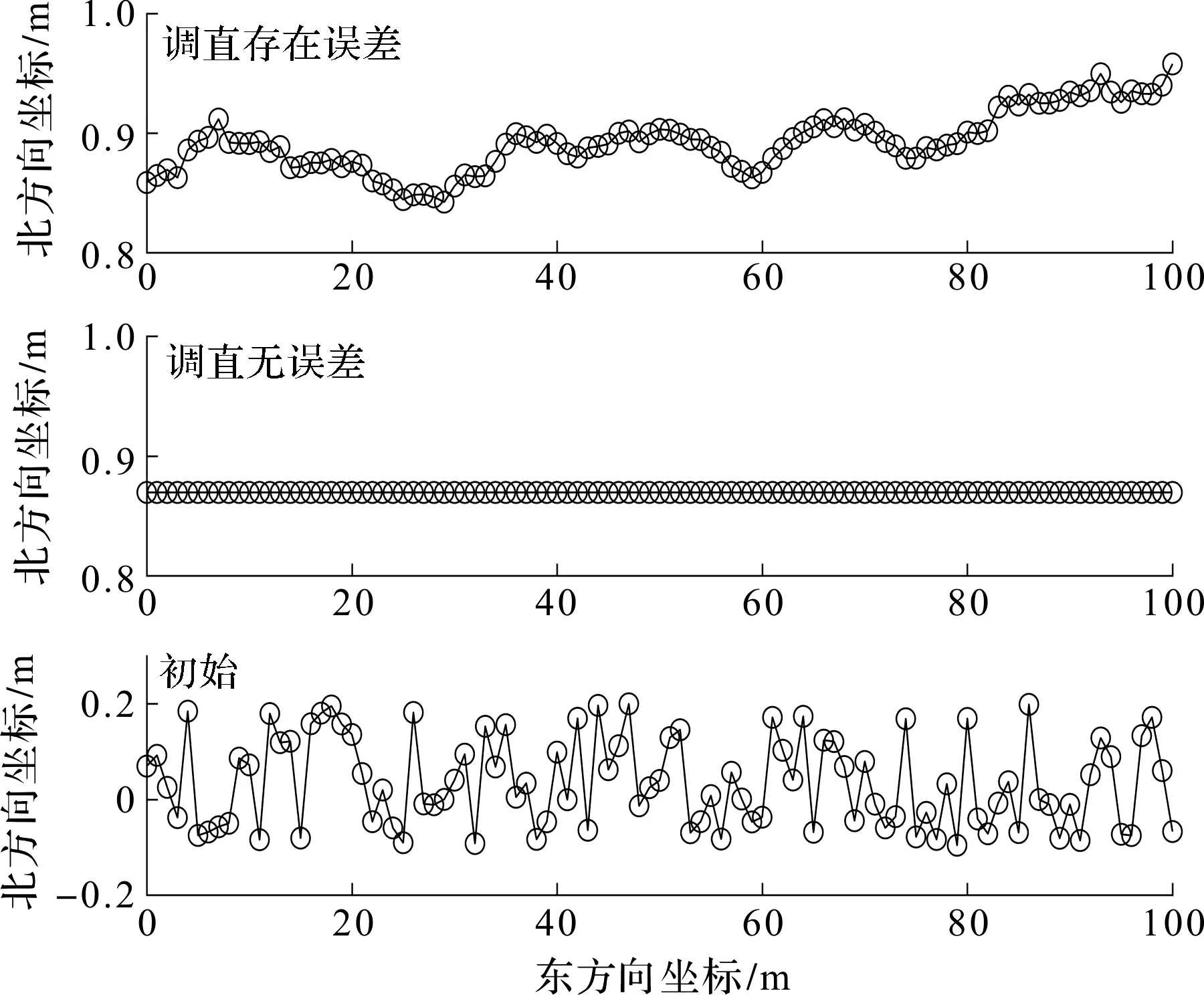
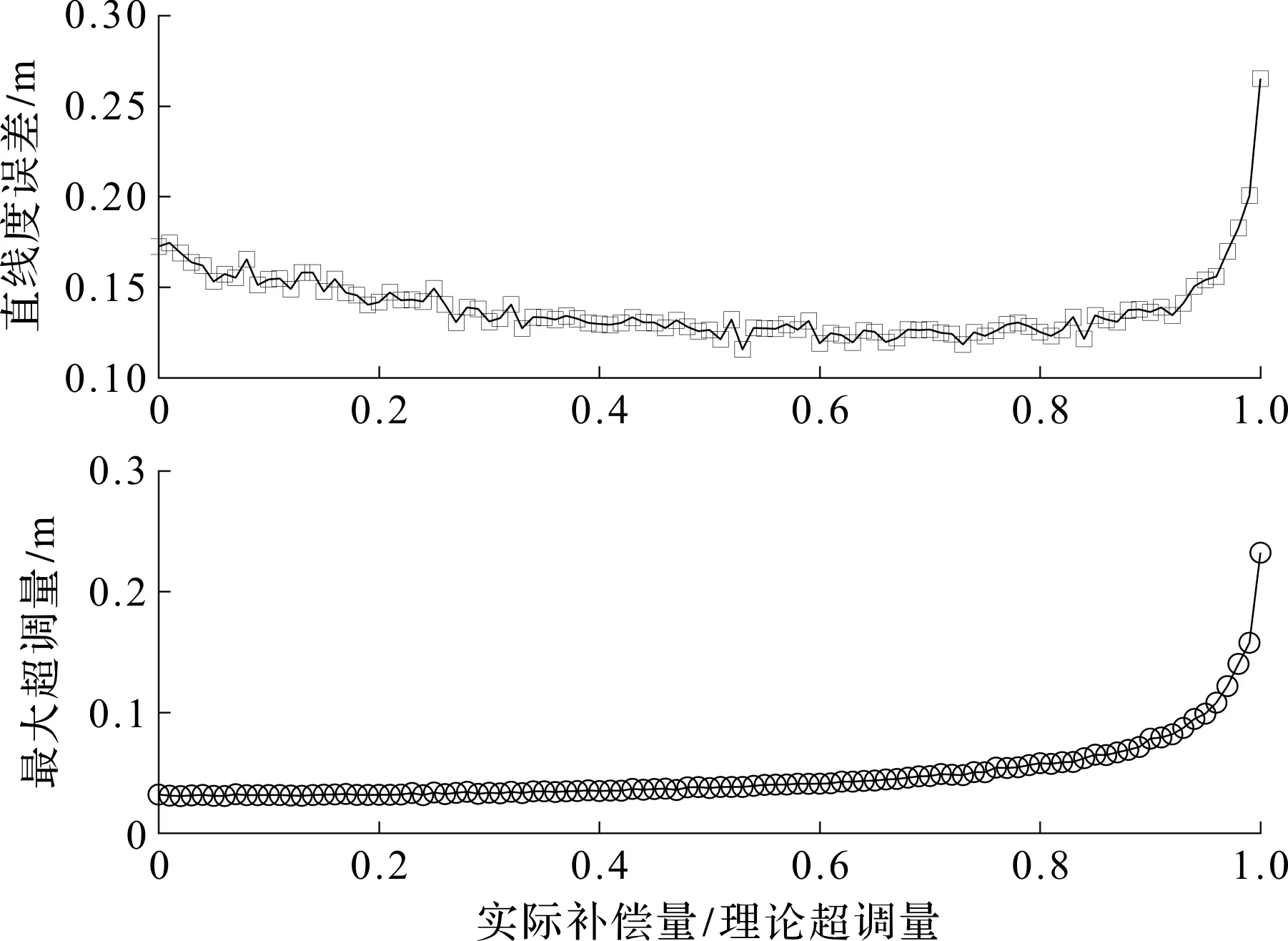
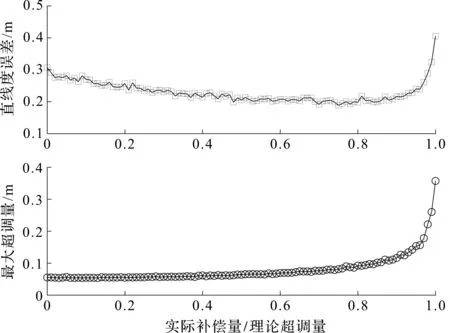
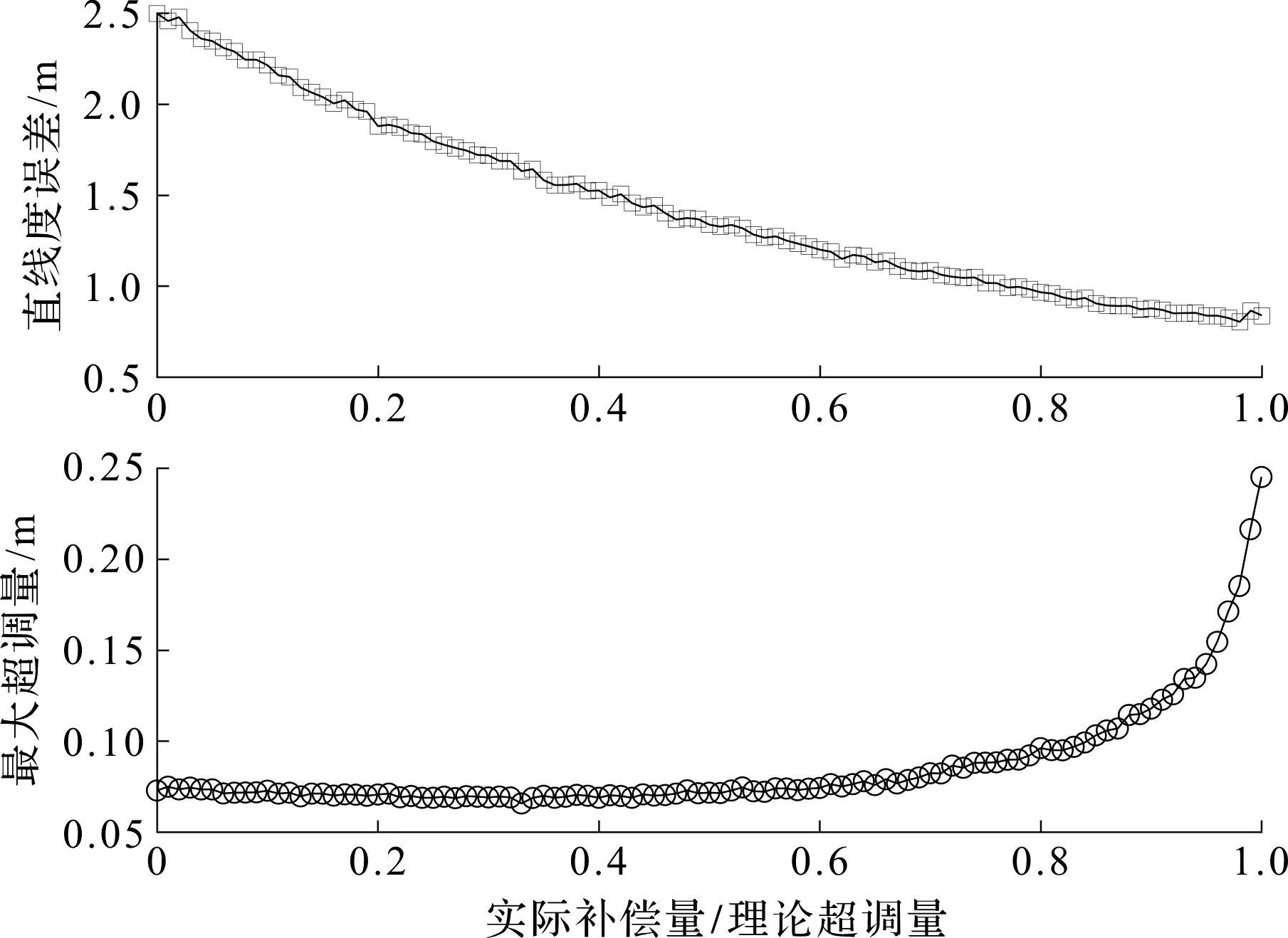
当N=0时,不补偿超调量;当N=1时,对超调量进行完全补偿;当0

(3)

(4)

Δh=yi-yj

(5)

(6)

式中:μ—误差均值,m;Δp—测量推移距离误差的偏差,m;Δq—测量超调量误差的偏差,m;Δo—执行误差的偏差,m;Δh—直线度误差,m。

yi是由无数个误差积累而成,整体直线呈现为一条平缓的曲线;直线度误差Δh为yi最大值减去最小值如式(5)所示,i点和j点分别是最突出点和最滞后点。直线度误差大小由两点之间的累计误差构成,因此直线度误差由测量误差和推移误差(δp,δq,δo)决定;并且液压支架的稳态直线度误差只与本次调直误差有关,不受其他过程的调直误差影响。

并且i和j相差越大,δpj、δoj、δqj的系数就越靠近某个小于1的数。这时N取值越大,可以使δp、δo和δq所乘的系数最小,从而极大减小误差累积,使直线度误差减小。由式(4)可知,若误差均值μp+μo+μq不为0,会导致推移曲线推斜。

式(6)表明,超调量是由误差累积而成,而补偿系数抑制了超调量的误差累积。i每增大1,所有误差会乘一个小于1的系数N,使得bi误差累积不明显;即使当bi比较大时,随着i的增大,累积的误差也会因为趋近0的系数而快速减小,使得超调量保持在一定范围内;并且N取值越小,对超调量bi改善越明显。

3 仿真及结果分析

笔者利用MATLAB软件进行数值仿真,对调直效果进行检验。在东北天坐标系中,工作面沿着东方向分布,推进方向向北,假设液压支架中心距间距为1.00 m,并假设标准推移距离H为0.8 m;液压支架传感器测量误差δp、δq和液压支架推移执行误差δo为影响液压支架直线度的主要因素;假设误差δp、δq和δo为相互独立的随机变量,并服从正态分布。

在δp、δq和δo服从不同正态分布情况下,本文对液压支架动态调直进行数值仿真实验;引用直线度误差和最大超调量来评价直线度(直线度误差定为最大值减去最小值,最大超调量为工作面中所有相邻液压支架之间纵向相差距离的最大值)。

算法仿真实验条件如表1所示。

表1 液压支架调直算法仿真条件表

表1中,用仿真实验Ⅰ对于液压支架调直方法的原理进行验证;用仿真实验Ⅱ～Ⅳ通过设置不同的初始条件,对补偿系数N的效果进行验证。

(1)液压支架测量和推移执行无误差与存在误差条件下,液压支架的动态调直过程如图3所示。

图3 仿真实验Ⅰ

第1台液压支架按照标准距离H推移后,其后所有的支架通过对比前一支架算出推移补偿距离。调直为理想直线,即直线度误差Δh=0。说明该调直方法理论上是正确的。假设液压支架测量无误差,液压支架推移误差δo～N(0,0.0082),补偿系数为0。由于误差的存在,使得调直不可能完全对齐。在未调直前直线度误差Δh=0.296 7 m;调直后直线度误差Δh=0.115 5 m,曲线直线度误差下降。

(2)假设液压支架测量误差δp、δq～N(0,0.0082),液压支架推移误差δo～N(0,0.0082),液压支架推移110次。

液压支架直线度误差均值和最大超调量值随补偿系数N的变化情况,如图4所示。

图4 仿真实验Ⅱ

直线度误差呈现U字形,直线度误差可降低至完全补偿的三分之一;最大超调量在[0,0.8]区间随着N缓慢变大,并且在[0.8,1]快速增大。因此在该误差条件下,N在[0.3,0.8]范围内调直效果明显改善。

(3)假设液压支架测量误差δp、δq～N(0,0.0082),液压支架推移误差δo～N(0,0.0182)，液压支架推移110次。

液压支架直线度误差均值和最大超调量值随补偿系数N的变化如图5所示。

图5 仿真实验Ⅲ

直线度误差呈现U字形。直线度误差可降低至完全补偿的二分之一。最大超调量在[0,0.8]区间随着N缓慢变大,并且在[0.8,1]快速增大。因此在该误差条件下,N在[0.3,0.8]范围内调直效果明显改善。

(4)假设液压支架测量误差δp、δq～N(0.01,0.0082),液压支架推移误差δo～N(0.015,0.0182),液压支架推移110次。

液压支架直线度误差均值和最大超调量值随补偿系数N的变化情况,如图6所示。

图6 仿真实验Ⅳ

图6中,直线度误差呈现下降趋势。再由式(4)可知:由于偏差均值不为零,使得误差累积,使得整个工作面朝一个方向偏移,变成一条斜线;当N增大时,由于补偿的存在,使得斜线斜率减小。

在实际工程实践中,由于液压支架上每个传感器都是独立的,所有传感器误差均值都不同,这种误差均值偏向同一侧的情况可能性很小。

4 结束语

笔者在已有的液压支架为基准的调直方法中引入补偿系数,通过理论分析,并利用MATLAB进行了数值仿真,仿真结果显示,综合考虑推移曲线的直线度误差和超调量,使用补偿系数的调直曲线明显优于不补偿和完全补偿的曲线。

由此可见,在已有的调直方法中引入补偿系数,能够有效地减少液压支架直线度误差和超调量的误差累积,并使直线度和超调量稳定在一定范围内;

同时,液压支架调直过程只与本次调直过程有关,与之前调直过程无关,这也在一定程度上避免了误差累积;选取合适的补偿系数N可以明显改善调直效果。